Похожие презентации:
Симметрия. Виды симметрии
1.
Я в листочке, я в кристалле,Я в живописи, архитектуре,
Я в геометрии, я в человеке.
Одним я нравлюсь, другие
Находят меня скучной.
Но все признают, что
Я – элемент красоты.
2. Симметрия. Виды симметрии
3.
«Симметрия является той идеей, спомощью которой человек веками
пытается объяснить и создать
порядок, красоту и совершенство»
Герман Вейль
4.
Цель урока:закрепить и обобщить знания по теме
«Симметрия»
1.
2.
Повторить осевую и центральную
симметрии;
Закрепить знания по видам
симметрии.
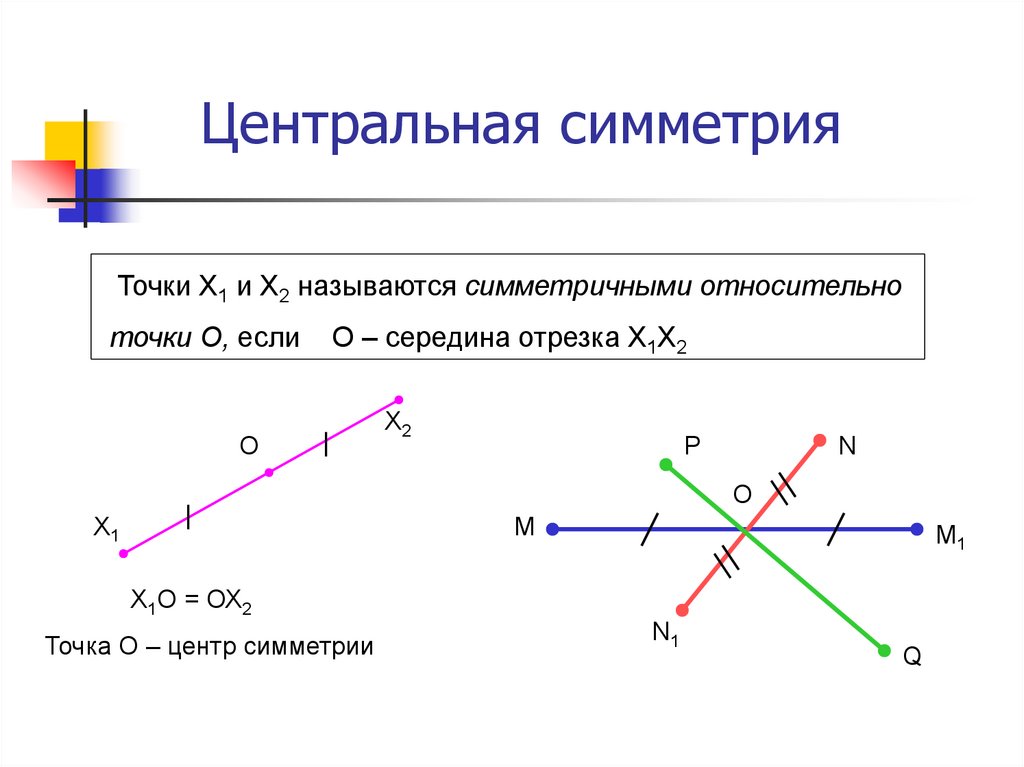
5. Центральная симметрия
Точки Х1 и Х2 называются симметричными относительноточки О, если
О – середина отрезка Х1Х2
О
Х2
Р
N
О
Х1
M
M1
Х1О = ОХ2
Точка О – центр симметрии
N1
Q
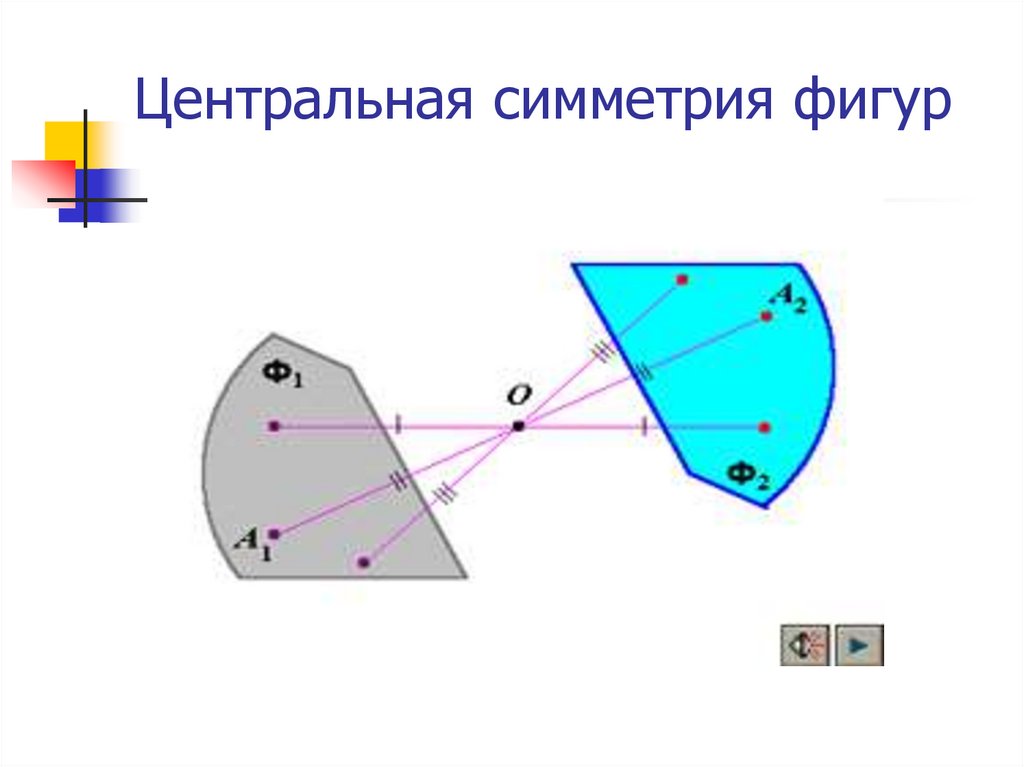
6. Центральная симметрия фигур
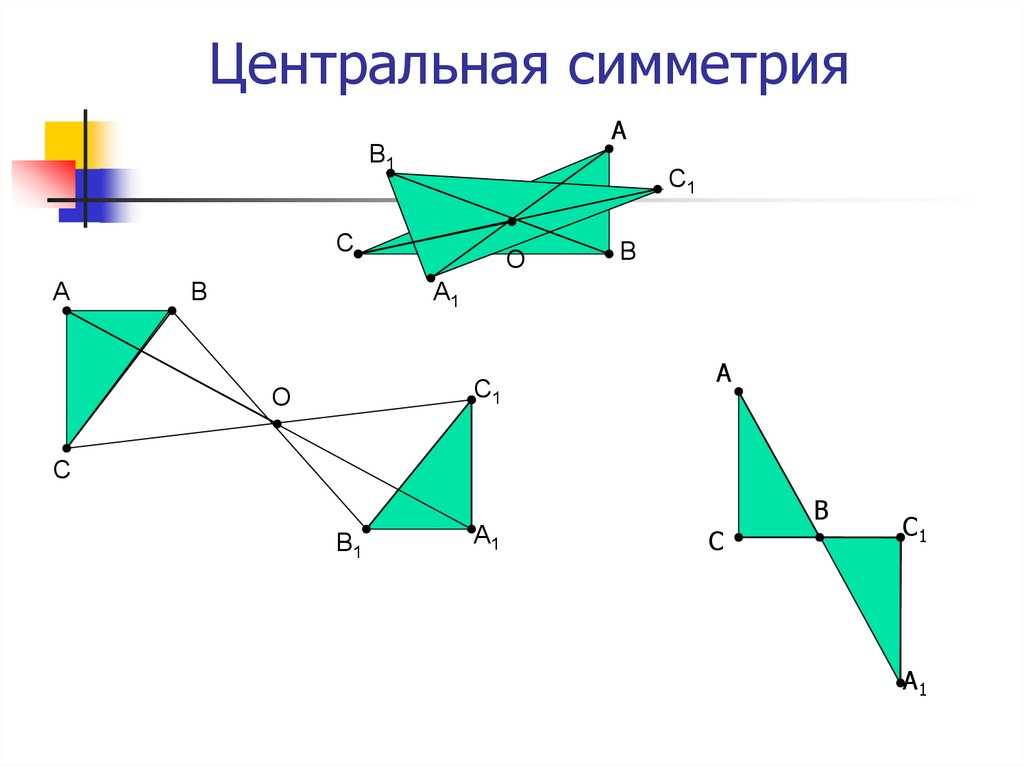
7. Центральная симметрия
АВ1
С1
С
А
В
О
В
А1
С1
О
А
С
В1
А1
С
В
С1
А1
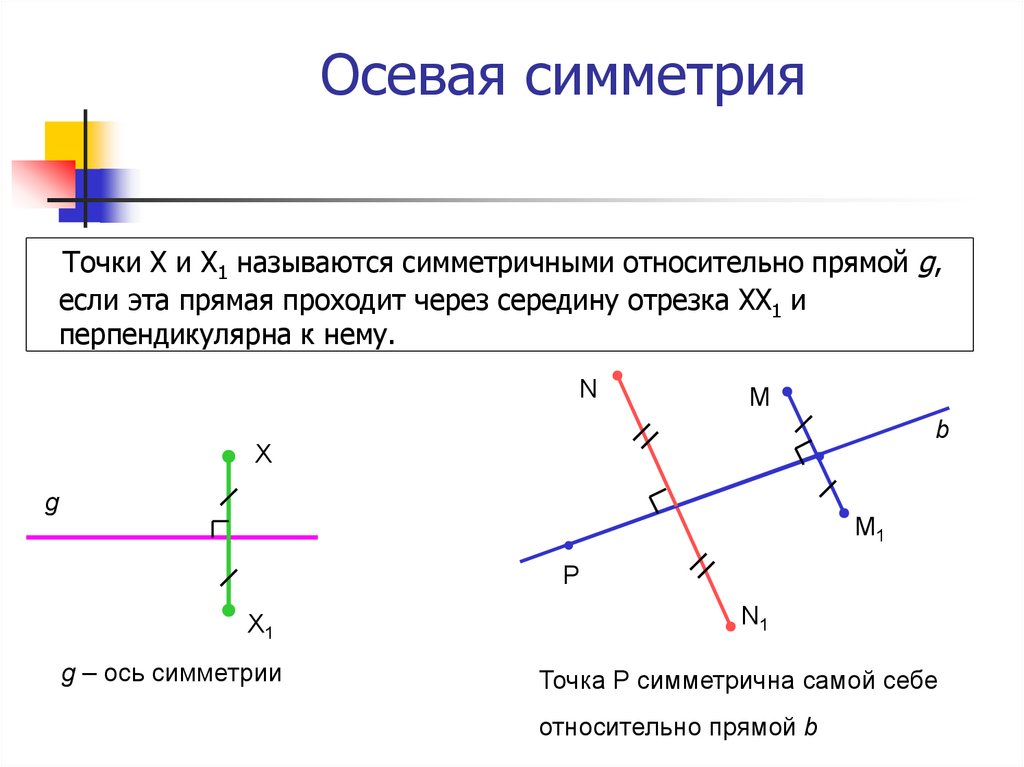
8. Осевая симметрия
Точки Х и Х1 называются симметричными относительно прямой g,если эта прямая проходит через середину отрезка ХХ1 и
перпендикулярна к нему.
N
М
b
Х
g
М1
Р
Х1
g – ось симметрии
N1
Точка Р симметрична самой себе
относительно прямой b
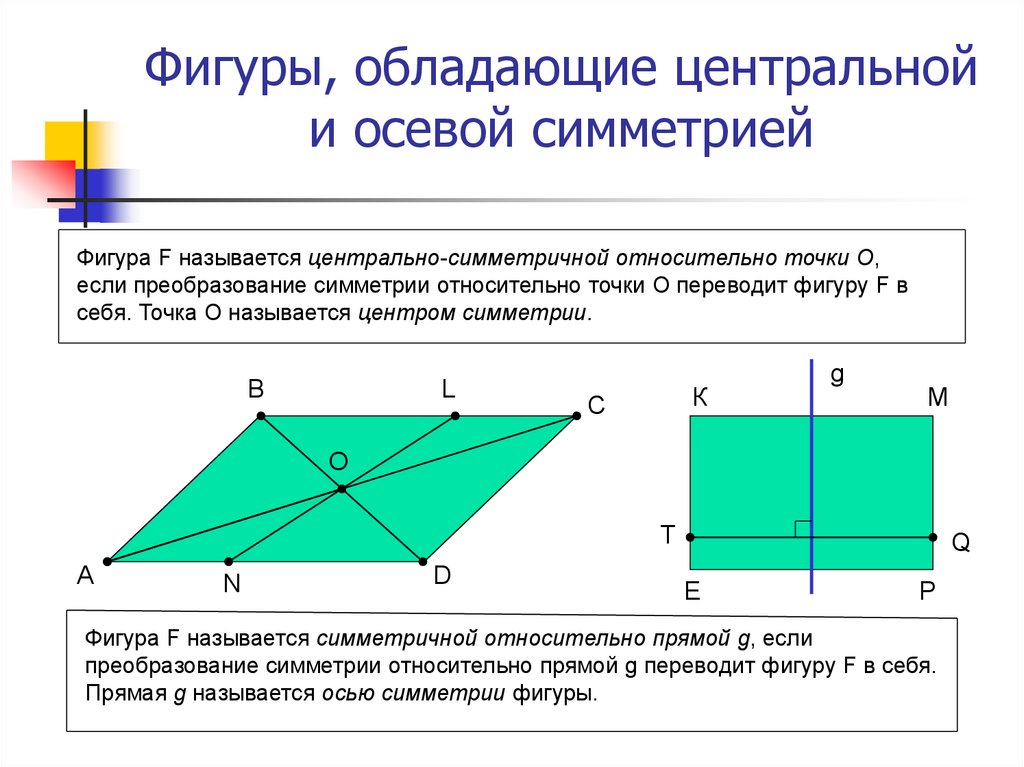
9. Фигуры, обладающие центральной и осевой симметрией
Фигура F называется центрально-симметричной относительно точки О,если преобразование симметрии относительно точки О переводит фигуру F в
себя. Точка О называется центром симметрии.
В
L
К
С
g
М
О
T
А
N
D
Q
E
P
Фигура F называется симметричной относительно прямой g, если
преобразование симметрии относительно прямой g переводит фигуру F в себя.
Прямая g называется осью симметрии фигуры.
10.
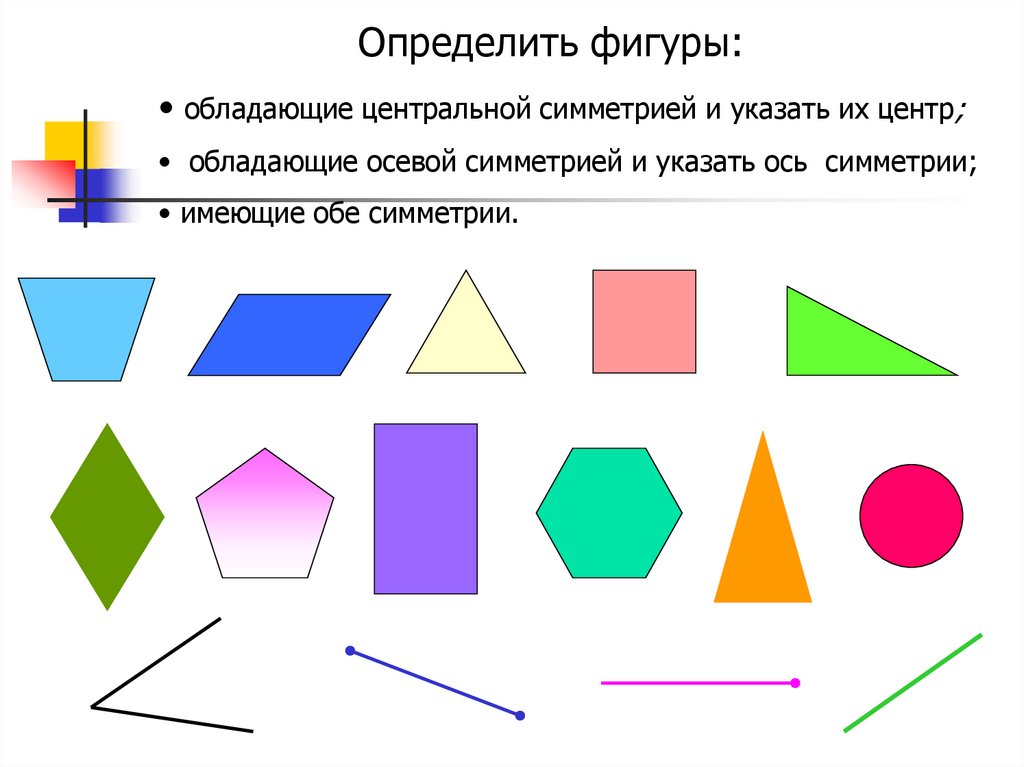
Определить фигуры:• обладающие центральной симметрией и указать их центр;
• обладающие осевой симметрией и указать ось симметрии;
• имеющие обе симметрии.
11.
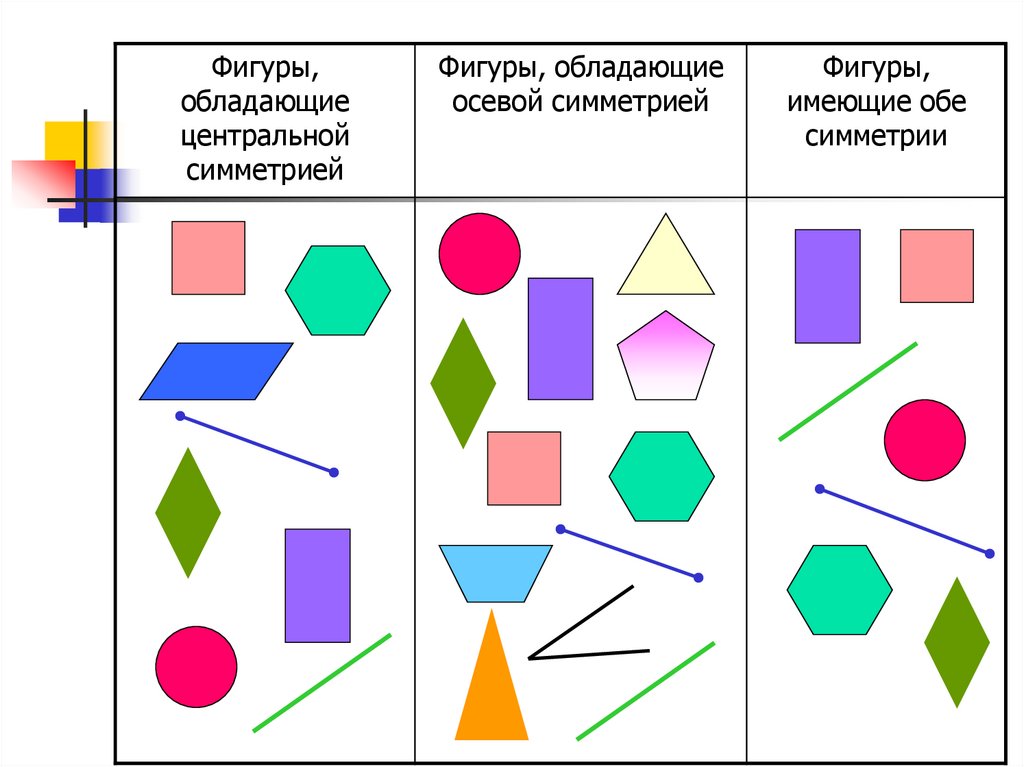
Фигуры,обладающие
центральной
симметрией
Фигуры, обладающие
осевой симметрией
Фигуры,
имеющие обе
симметрии
12.
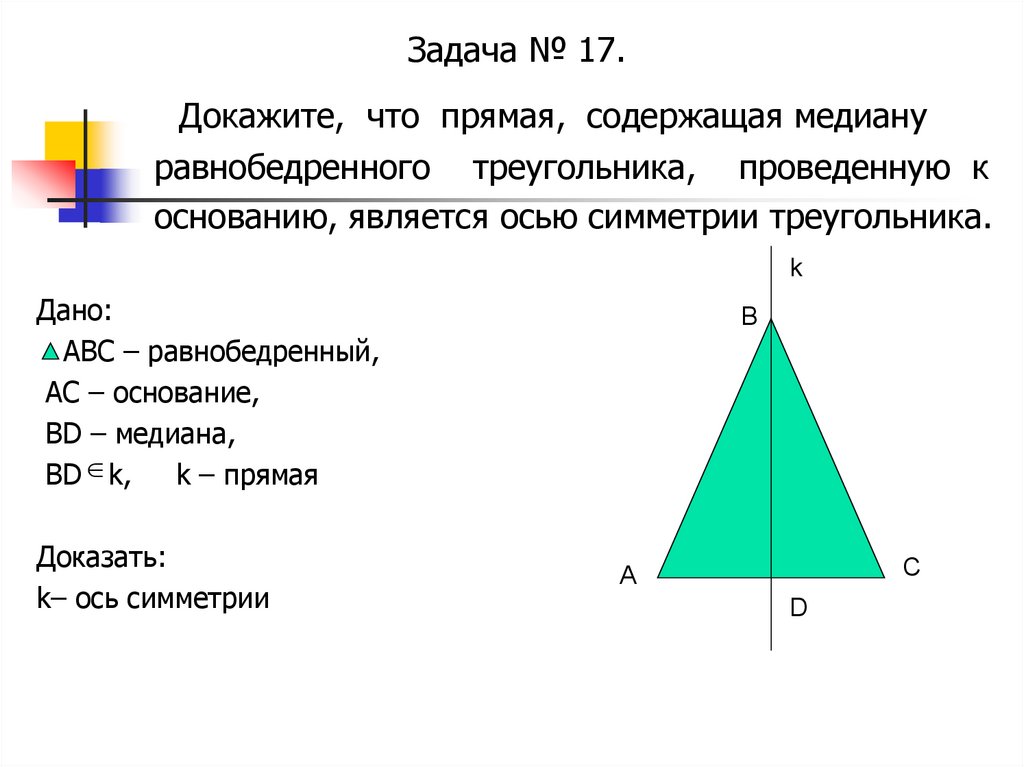
Задача № 17.Докажите, что прямая, содержащая медиану
равнобедренного треугольника, проведенную к
основанию, является осью симметрии треугольника.
k
Дано:
АВС – равнобедренный,
АС – основание,
ВD – медиана,
ВD k,
k – прямая
Доказать:
k– ось симметрии
В
С
А
D




 Математика
Математика








