Похожие презентации:
Ядерная гамма-резонансная спектроскопия
1.
Тема № 8Ядерная
гамма резонансная
спектроскопия
2.
СОДЕРЖАНИЕ:История открытия
Ядерное резонансное поглощение гамма излучения
Техника месбауэровского эксперимента
Сверхтонкие взаимодействия и мессбауэровские
параметры
Практические применения метода:
- Фазовый анализ в материаловедении и геохимии
- Анализ поверхности
- Динамические эффекты
3. История открытия ядерного гамма резонанса (эффекта Мессбауэра)
Атомный резонансный процесс в оптическом диапазоне длинволн хорошо известен. Он был предсказан Д. Релеем и нашел свое
экспериментальное подтверждение в 1904 г. в известном опыте Роберта
Вуда, в котором Вуд использовал желтый свет, испускаемый атомами
натрия (так называемые D-линии натрия), который можно получить,
поместив в пламя небольшое количество поваренной соли. Каждой D –
линии соответствует собственная частота колебаний атома натрия, или,
более точно, внешних электронов этого атома. Чтобы наблюдать резонанс,
необходимо иметь другие атомы натрия, не находящиеся в пламени. Вуд
использовал откачанный стеклянный баллон, содержащий небольшое
количество металлического натрия. Давление паров натрия таково, что
при нагревании выше комнатной температуры количество паров натрия
в баллоне было достаточным для проведения опыта. Если свет от
натриевого пламени сфокусировать на баллон, то можно наблюдать
появление слабого желтого свечения. Атомы натрия в колбе действуют
аналогично настроенному камертону. Они поглощают энергию
падающего пучка желтого света, а затем высвечивают ее в разные
стороны.
4.
Пятьдесят лет назад, в 1958 году,немецкий физик 1958 года Рудольф
Людвиг Мёссбауэр, работая над
диссертацией доктора философии в
Институте им. М. Планка в
Гейдельберге, представил в немецкий
физический
журнал
статью
с
названием
«Ядерная резонансная
флуоресценция гамма излучения в
Ir191», которая была опубликована в
середине того же года. А уже осенью
1958
года,
выполнил
первые
эксперименты, в которых для
сканирования резонансных линий
использовал эффект Доплера.
В конце 1958 года, он опубликовал полученные экспериментальные
данные, заложившие основу нового экспериментального метода –
ядерной гамма-резонансной спектроскопии, которая часто называется
Мёссбауэровской спектроскопией (МС). В 1961 году за открытие и
теоретическое обоснование этого явления Рудольфу Мессбауэру была
присуждена Нобелевская премия по физике.
5. Влияние эффекта отдачи при поглощении и испускании гамма излучения ядрами
E ист ET E R E D2
ER T 2
2McE
Энергия отдачи:
57Fe
E погл. ET E R E D
E R E /( 2 Mc )
2
2
Энергия Допплера:
E D E ( 2 T / Mc 2 )1 / 2
: ET = 14.4 кэВ, t1/2 = 98 нс, Г = 4.6·10-9 эВ, → ER~ 2·10-3 эВ
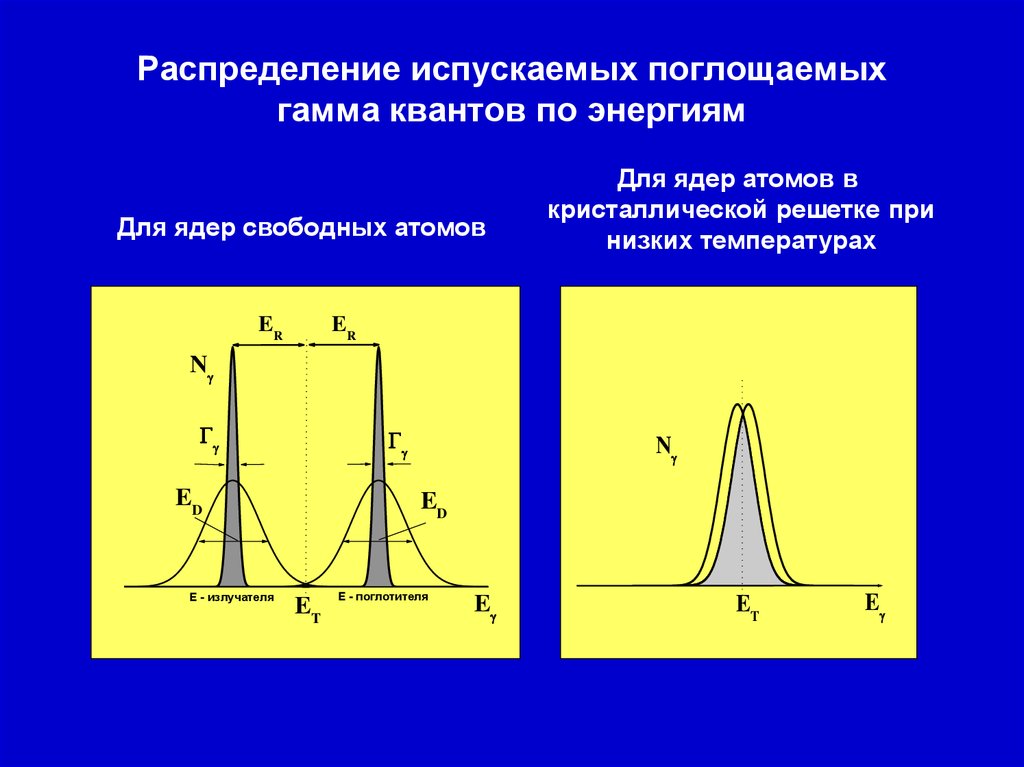
6. Распределение испускаемых поглощаемых гамма квантов по энергиям
Для ядер свободных атомовДля ядер атомов в
кристаллической решетке при
низких температурах
ER
ER
N
ED
E - излучателя
N
ED
ET
E - поглотителя
E
ET
E
7. Сравнение основных параметров между электронными и ядерными переходами
Параметры переходовЭнергия перехода,
ЕТ (эВ)
Среднее время жизни
возбужденного состояния,
(сек)
Естественная ширина
резонансной линии,
Γ=ħ/τ (эВ)
Энергетическое разрешение,
Г/ЕТ
Энергия отдачи,
ЕR (эВ)
Отношение ЕR/Г
Электронный
переход для
D-линии Na
Ядерный
переход
57Fe
Ядерный
переход
119Sn
2.1
14 413
23 800
1.5×10-8
1.4×10-7
2.8×10-8
4.4×10-8
4.6×10-9
2.4×10-8
2.1×10-8
3.1×10-13
1×10-12
~10-10
1.9×10-3
2.5×10-3
~2.3×10-3
4.1×105
1.4×105
8. Ядерные параметры основных Мессбауэровских изотопов
Изотоп57Fe
61Ni
119Sn
121Sb
125Te
127I
129I
149Sm
151Eu
161Dy
193Ir
197Au
237Np
Eγ,
кэВ
Гr/(ммс-1)
=2Гест
Ig
Ie
14.41
67.40
23.87
37.15
35.48
57.60
27.72
22.5
21.6
26.65
73.0
77.34
59.54
0.192
0.78
0.626
2.1
5.02
2.54
0.59
1.60
1.44
0.37
0.60
1.87
0.0067
1/23/21/2+
5/2+
1/2+
5/2+
7/2+
7/25/2+
5/2+
3/2+
3/2+
5/2+
3/25/23/2+
7/2+
3/2+
7/2+
5/2+
5/27/2+
5/21/2+
1/2+
5/2-
α
8.17
0.12
5.12
~10
12.7
3.70
5.3
~12
29
~2.5
~6
4.0
1.06
Природное
содержание
%
2.17
1.25
8.58
57.25
6.99
100
nil
13.9
47.8
18.88
61.5
100
nil
Распад ядра
57Co
(EC 270d)
61Co (ß-99m)
119mSn (IT 50d)
121mSn (ß-76y)
125I (EC 60d)
127mTe (ß-109d)
129mTe (ß-33d)
149Eu (EC 106d)
151Gd (EC 120d)
161Tb (ß-6.9d)
193Os (ß-31h)
197Pt (ß-18h)
237Am (α 458y)
ЕС-электронный захват, ß –бета распад, IT- изомерный переход, α- альфа распад
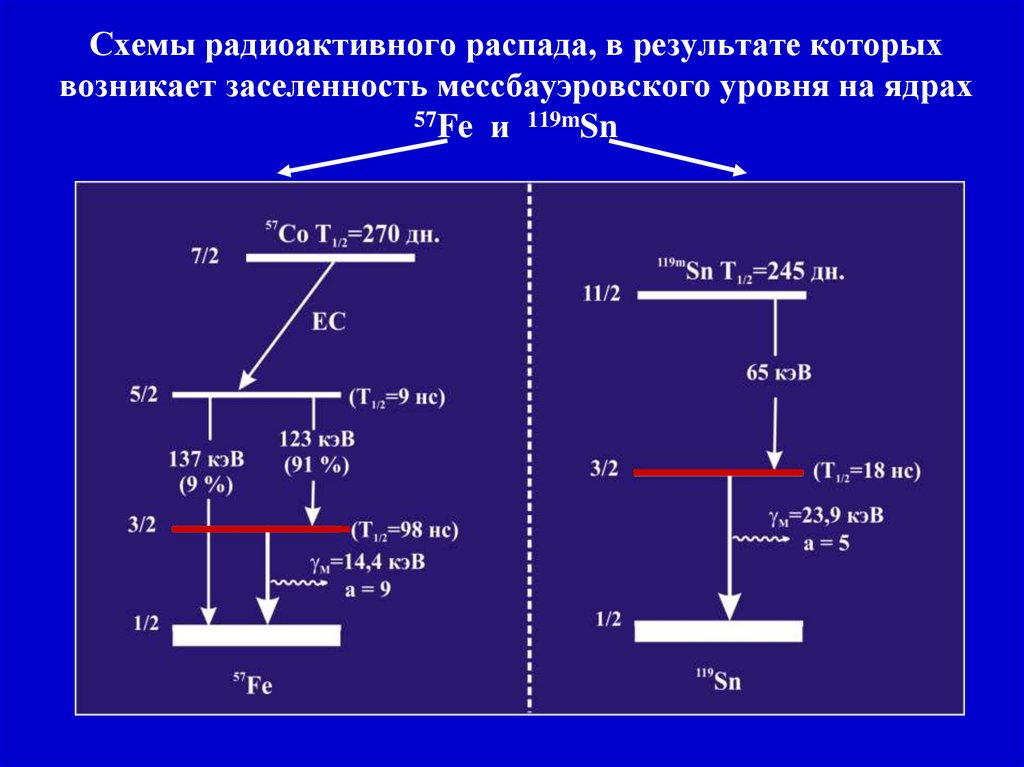
9. Схемы радиоактивного распада, в результате которых возникает заселенность мессбауэровского уровня на ядрах 57Fe и 119mSn
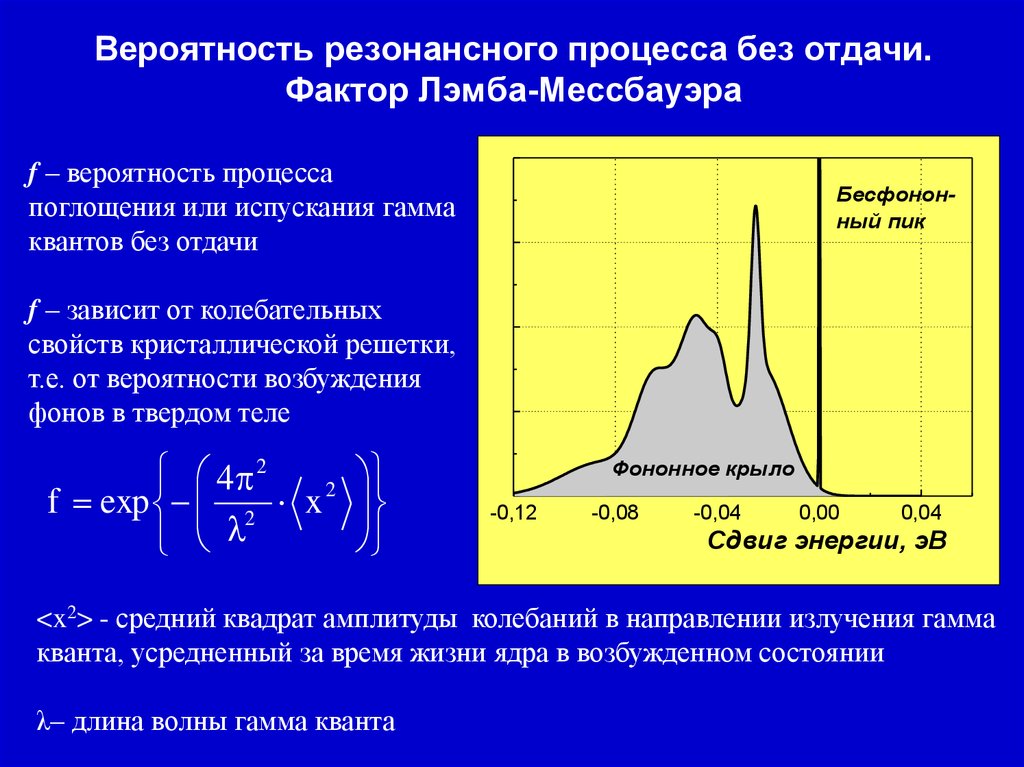
10. Вероятность резонансного процесса без отдачи. Фактор Лэмба-Мессбауэра
f – вероятность процессапоглощения или испускания гамма
квантов без отдачи
Бесфононный пик
f – зависит от колебательных
свойств кристаллической решетки,
т.е. от вероятности возбуждения
фонов в твердом теле
4 2
2
f exp 2 x
Фононное крыло
-0,12
-0,08
-0,04
0,00
0,04
Сдвиг энергии, эВ
<x2> - средний квадрат амплитуды колебаний в направлении излучения гамма
кванта, усредненный за время жизни ядра в возбужденном состоянии
λ– длина волны гамма кванта
11. Влияние фононных процессы на поглощение или рассеяние без отдачи
cc
c
1,0
0,8
QD= 450
350
f
300
0,6
250
200
150
0,4
Ëèòèé
100
0,2
50
а
E
б
D
в
0,0
13
-1
5*10 ñåê
Колебательные спектры решеток
твердого тела
а – модель Эйнштейна, б-модель Дебая,
в- модель Борна-Кармана
0
100
200
300
400
500
600
T, K
2
D
T
3E R
x
T
f (T ) exp
(1 4 x dx( ) )
e 1 D
0
2k D
12. Необходимые условия для наблюдения эффекта Мессбауэра
1. Значения энергии γ-квантов должны лежать в пределах 10< Еγ <150 кэВ,т.е. энергия ядерных переходов должна быть достаточно велика, но
энергия отдачи не должна превышать энергии колебательных квантов
решетки.
2. Период полураспада мессбауэровского возбужденного ядра должен лежать
в пределах 1 < t1/2 < 100 нс, т.е. время жизни мессбауэровского уровня
должно быть достаточно большим, чтобы принцип неопределенности не
мог сильно сказываться на измерении ЕТ, но и достаточно малым, чтобы
получились досточно интенсивные и широкие линии.
3. У излучателя (источника) должен быть долгоживущий предшественник –
материнский радиоактивный изотоп. Распад этого изотопа должен
происходить через стадию образования мессбауэровского уровня.
Основное состояние изотопа должно быть устойчиво, а сечение
поглощения должно быть достаточно велико. Необходимо или
достаточное природное содержание этого изотопа, или возможность легко
проводить обогащение.
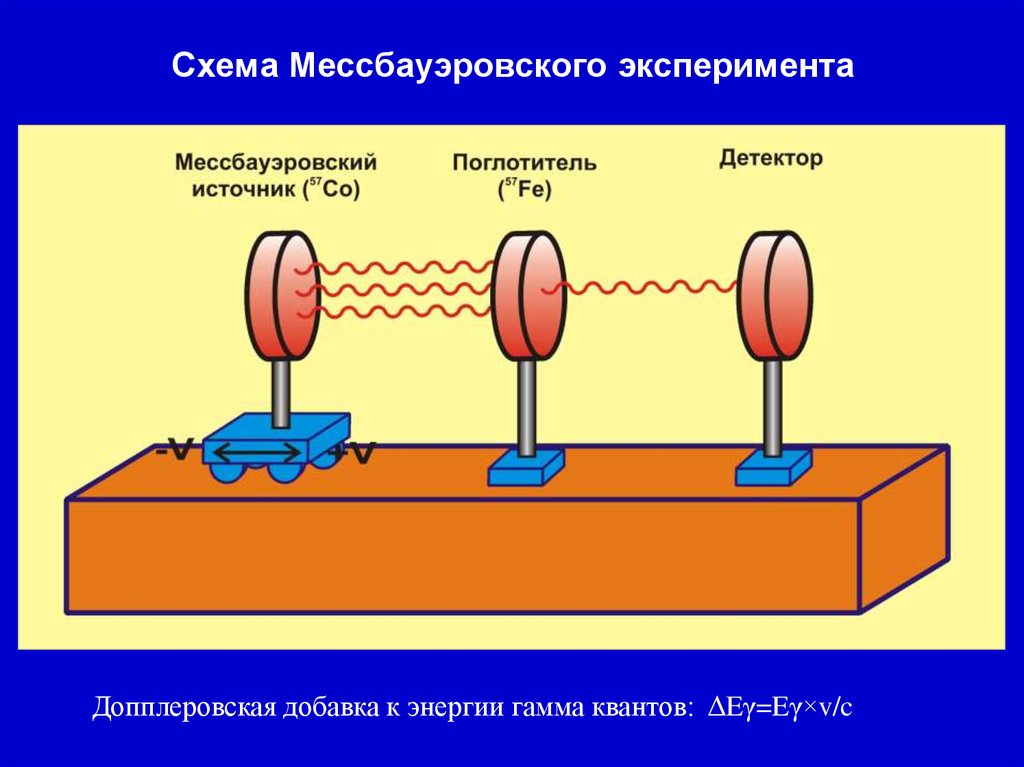
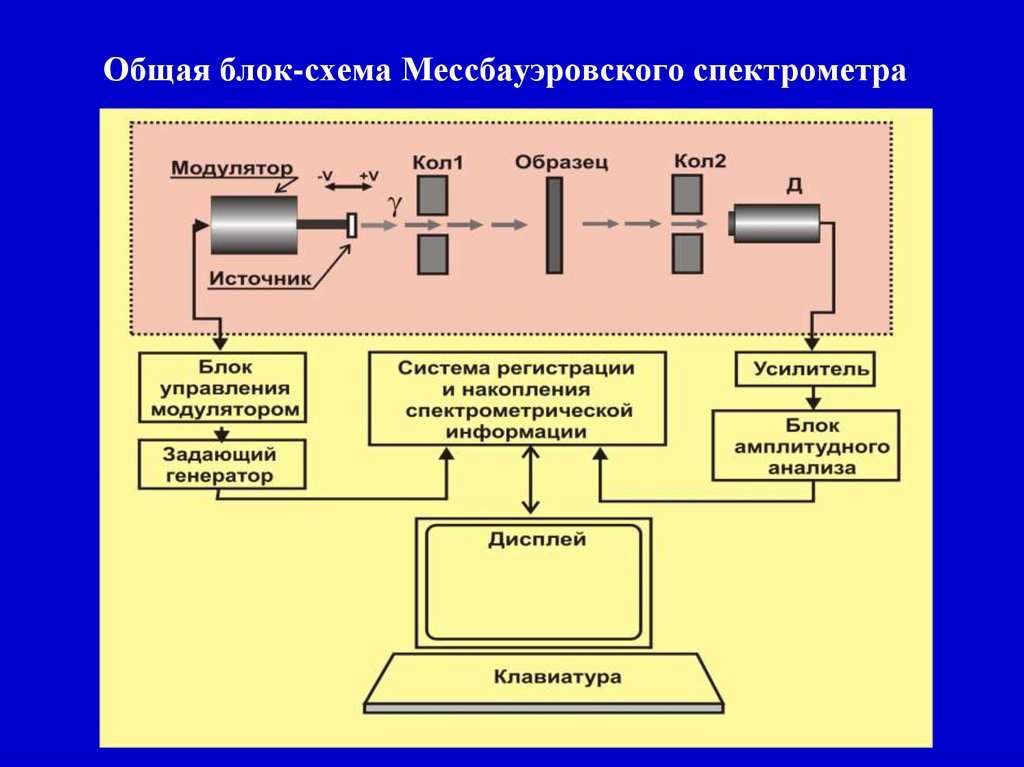
13. Схема Мессбауэровского эксперимента
Допплеровская добавка к энергии гамма квантов: ΔEγ=Eγ×v/c14. Общая блок-схема Мессбауэровского спектрометра
15. СВЕРХТОНКИЕ ВЗАИМОДЕЙСТВИЯ МЕССБАУЭРОВСКИЕ ПАРАМЕТРЫ
Мессбауэровский Тип взаимодействияпараметр
Извлекаемая информация
Спиновое состояние атома
(HS, LS, IS)
Электроотрицательность
лигандов
Степень окисления
Электронная плотность
Изомерный
сдвиг
δ(мм/с)
Электрическое монопольное
(кулоновское) между ядрами и
протонами
Квадрупольное
расщепление
ΔЕQ(мм/с)
Электрическое квадрупольное
взаимодействие между квадрупольным моментом ядра и
неоднородным электрическим
полем
Молекулярная симметрия
Характеристика зонной
структуры
Спиновое состояние атома
(HS, LS, IS)
Магнитное
расщепление
ΔЕМ(мм/с)
Магнитное дипольное
взаимодействие между
магнитным моментом ядра и
магнитным полем
Характер и величина
магнитного
взаимодействия
(ферромагнетизм,
антиферромагнетизм и т.д.
16. Электрическое монопольное взаимодействие Изомерный сдвиг δ
ИсточникПоглотитель 1
Ie
Поглотитель 2
Ie
ETS
ETА2
ETА1
Ig
Ig
Ie
Ig
-V
0
+V
-V
0
+V
4
2
2
2
Ze ( 0 ) Ï ( 0 ) È ( R / R ) R 2
5
4 c
vD
5 E
2 2
Ze R R / R ( 0 ) 2 ( 0 ) 2
Ï
È
17. Изомерный сдвиг в железосодержащих соединениях
При экспериментальном измерении изомерных химическихсдвигов всегда важно, какой
используется стандарт, относительно которого будут определяться
эти сдвиги.
Fe(I) S=2
Fe(I)
Fe(I) S=1/2
Fe(II) S=2
Fe(II) S=1
Fe(II)
Fe(II) S=0
Fe(III) S=5/2
Так для измерений на 57Fe официальным стандартом является
соединение этого изотопа
Na2[Fe(CN)5NO] или металлическое железо.
Fe(III) S=3/2
Fe(III)
Fe(III) S=1/2
Fe(IV) S=2
Fe(IV)
Fe(IV) S=1
Для 119mSn общепринятым
стандартом является SnO2.
Fe(VI)
Fe(VI) S=1
-1,0
-0,5
0
0,5
1,0
1,5
2,0
/мм с
-1
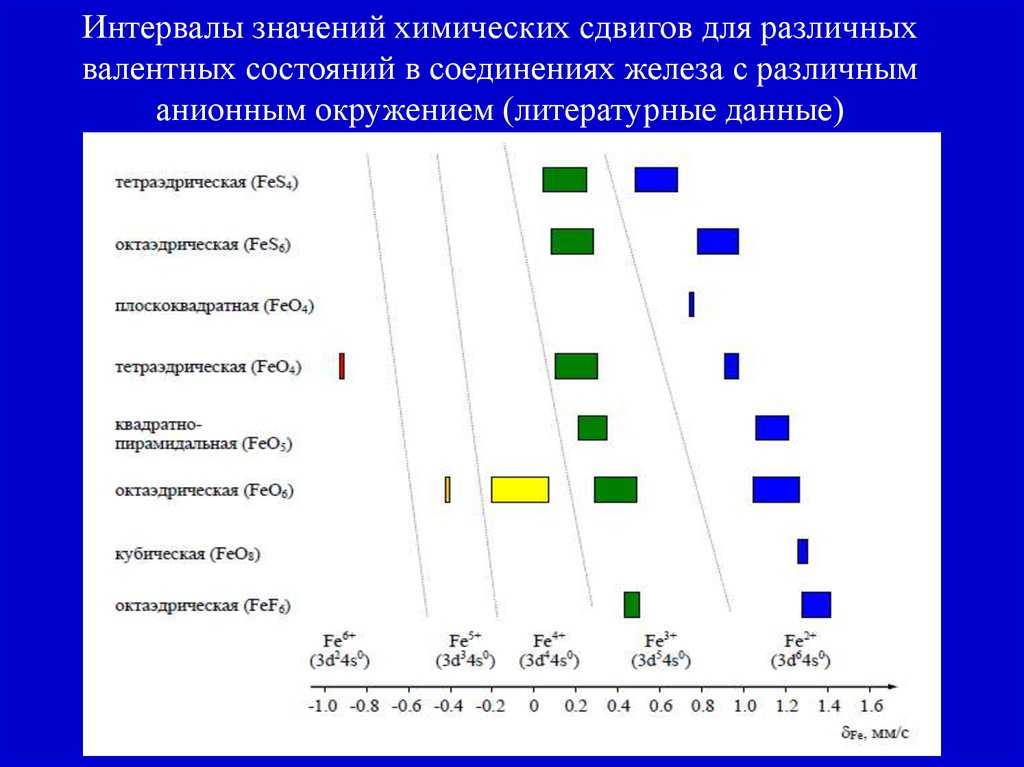
18.
Интервалы значений химических сдвигов для различныхвалентных состояний в соединениях железа с различным
анионным окружением (литературные данные)
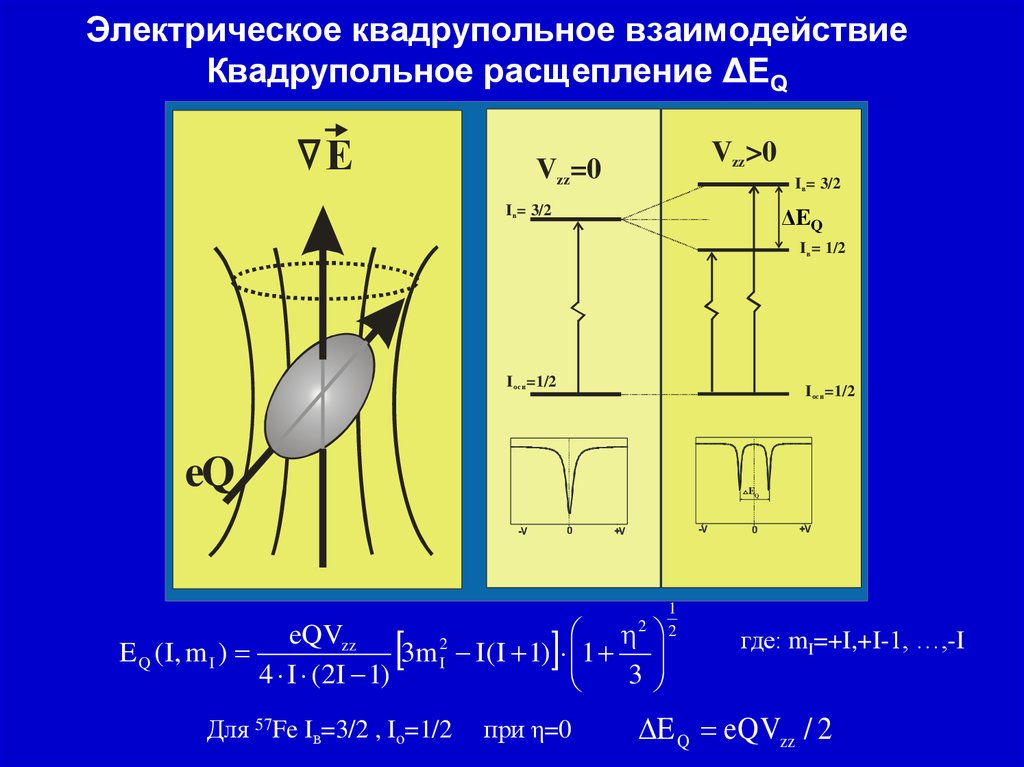
19. Электрическое квадрупольное взаимодействие Квадрупольное расщепление ΔЕQ
ЕVzz>0
Vzz=0
Iв = 3/2
Iв = 3/2
ΔEQ
I в = 1/2
Iосн=1/2
Iосн=1/2
eQ
EQ
0
-V
eQVzz
E Q ( I, m I )
3m 2I I( I 1)
4 I ( 2I 1)
Для 57Fe Iв=3/2 , Io=1/2
-V
+V
1
3
при η=0
2
1
2
0
+V
где: mI=+I,+I-1, …,-I
E Q eQVzz / 2
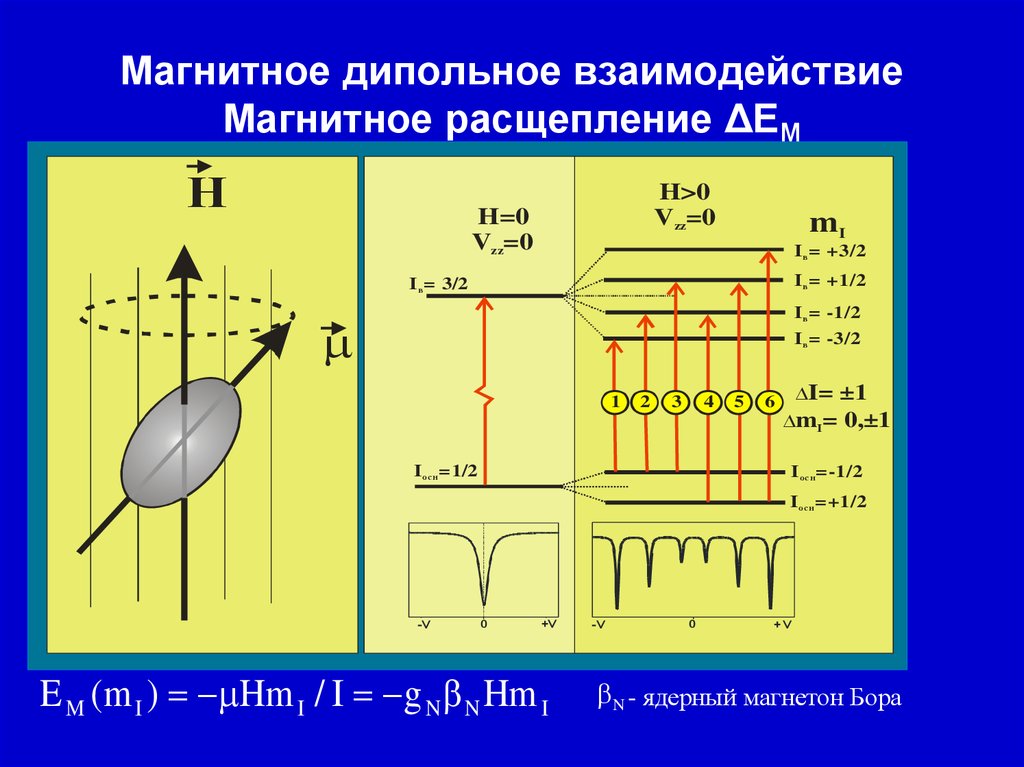
20. Магнитное дипольное взаимодействие Магнитное расщепление ΔЕМ
НH>0
Vzz=0
H=0
Vzz=0
mI
I в = +3/2
I в = +1 /2
I в = 3/2
I в = -1 /2
I в = -3/2
1
2
3
4
I осн=1/2
5
6
I=
±1
mI= 0,±1
I осн=-1/2
I осн=+1/2
-V
0
+V
E M ( m I ) Hm I / I g N N Hm I
-V
0
+V
N - ядерный магнетон Бора
21. Комбинированное магнитное дипольное и электрическое квадрупольное взаимодействие
H=0Vzz=0
Z
H=0
Vzz>0
H>0
Vzz>0
mI
H
I в = +3/2
I в = 3/2
I в = 3/2
I в = +1 /2
Y
I в = 1/2
I в = -1 /2
I в = -3/2
X
1
2
3
4
5
I=
±1
mI= 0,±1
6
H HM HQ
Обычно -
H Q H M
Для 57Fe и осевой
симметрии (η=0) :
I осн=1/2
I осн=-1/2
I осн=1/2
I осн=+1/2
EQ
-V
0
+V
-V
E M ,Q ( I, m I ) g N N Hm I ( 1)
0
m l 1 / 2
+V
-V
0
+V
(eQVzz / 8)(3 cos 2 1)
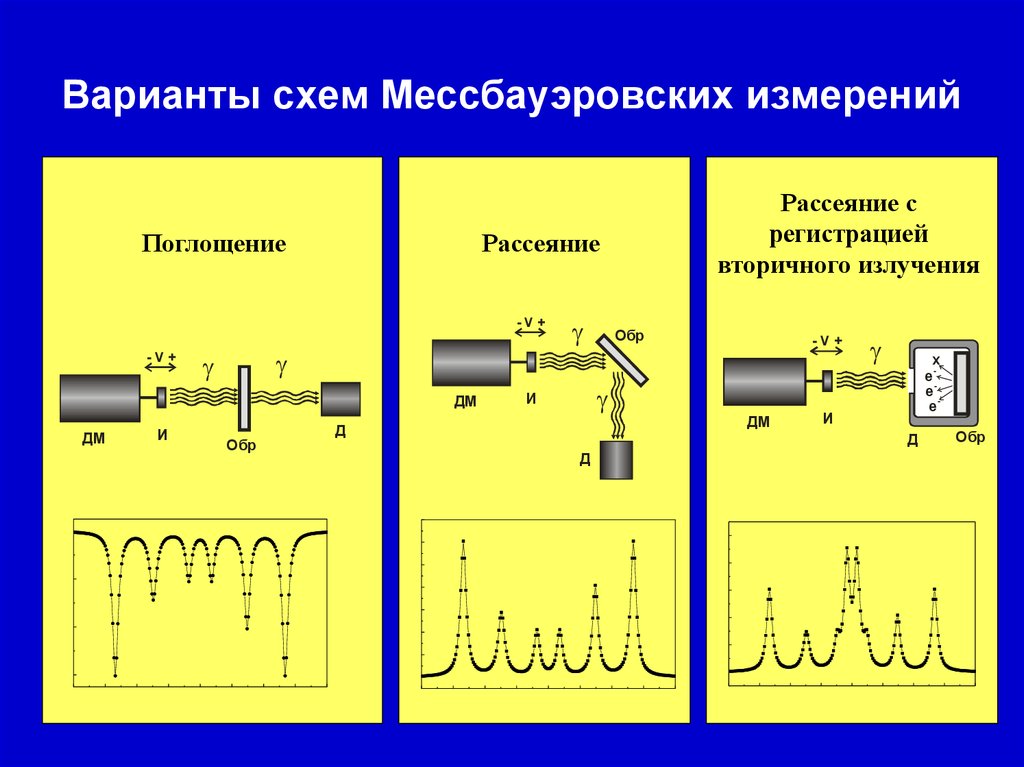
22. Варианты схем Мессбауэровских измерений
ПоглощениеРассеяние
-V+
-V+
ДМ
ДМ
И
Обр
Рассеяние с
регистрацией
вторичного излучения
Обр
И
Д
-V+
ДМ
x
e
e
e
И
Д
Д
Обр
23.
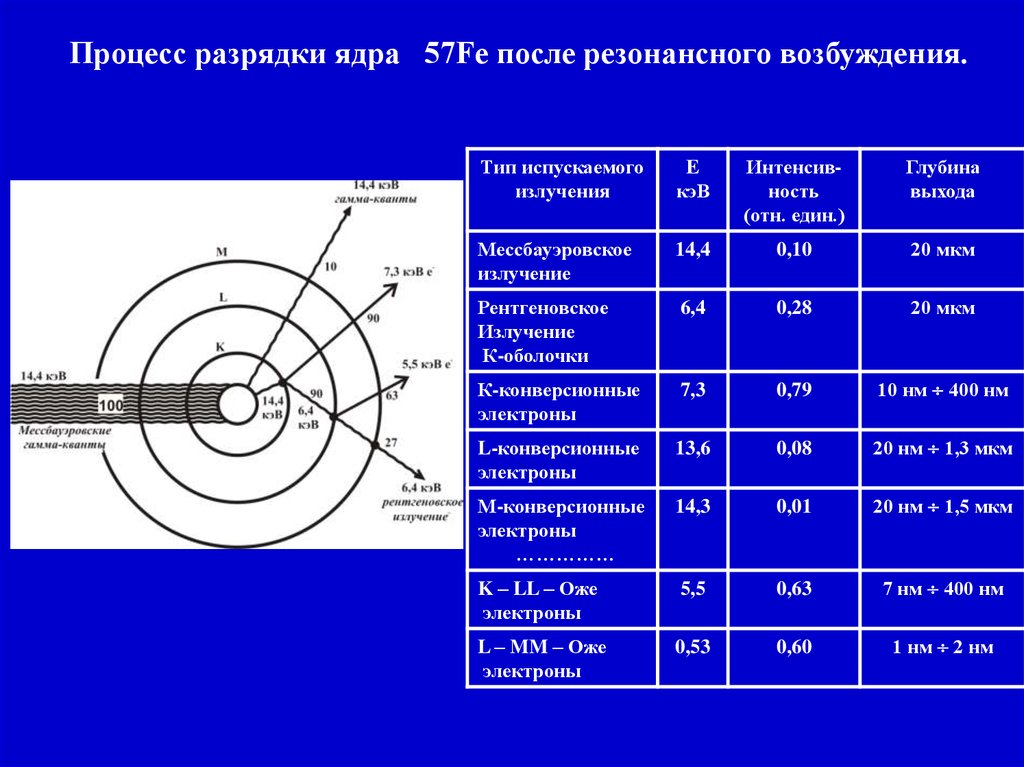
Процесс разрядки ядра 57Fe после резонансного возбуждения.Тип испускаемого
излучения
E
кэВ
Интенсивность
(отн. един.)
Глубина
выхода
Мессбауэровское
излучение
14,4
0,10
20 мкм
Рентгеновское
Излучение
К-оболочки
6,4
0,28
20 мкм
К-конверсионные
электроны
7,3
0,79
10 нм 400 нм
L-конверсионные
электроны
13,6
0,08
20 нм 1,3 мкм
М-конверсионные
электроны
……………
14,3
0,01
20 нм 1,5 мкм
K – LL – Оже
электроны
5,5
0,63
7 нм 400 нм
L – MM – Оже
электроны
0,53
0,60
1 нм 2 нм
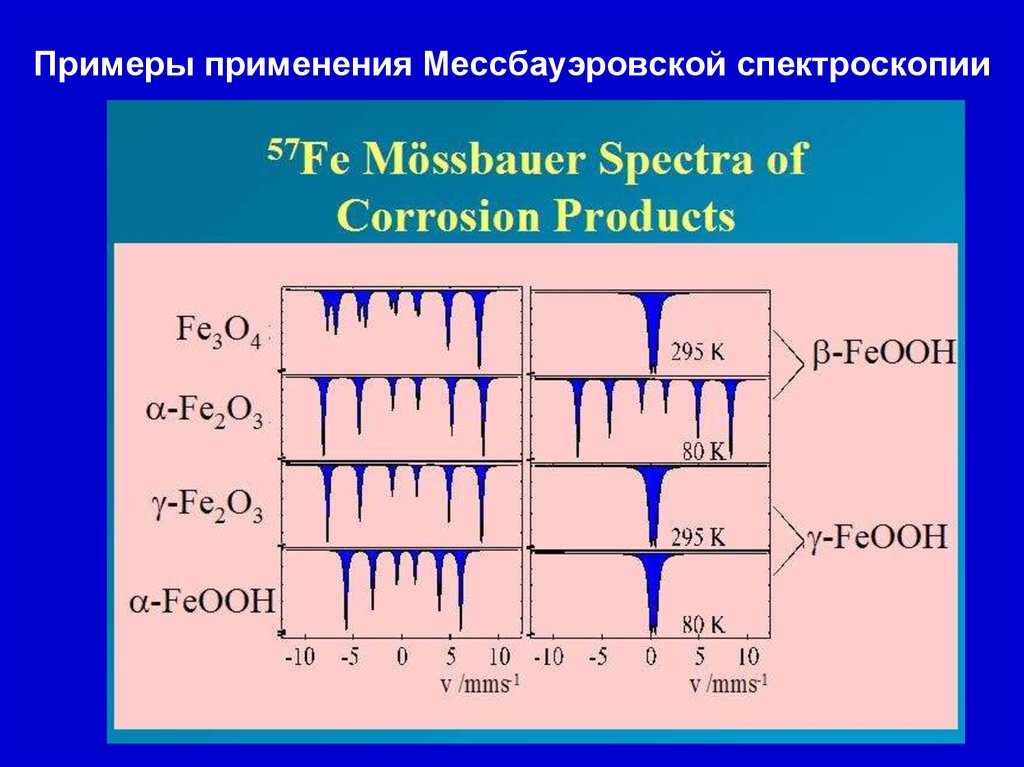
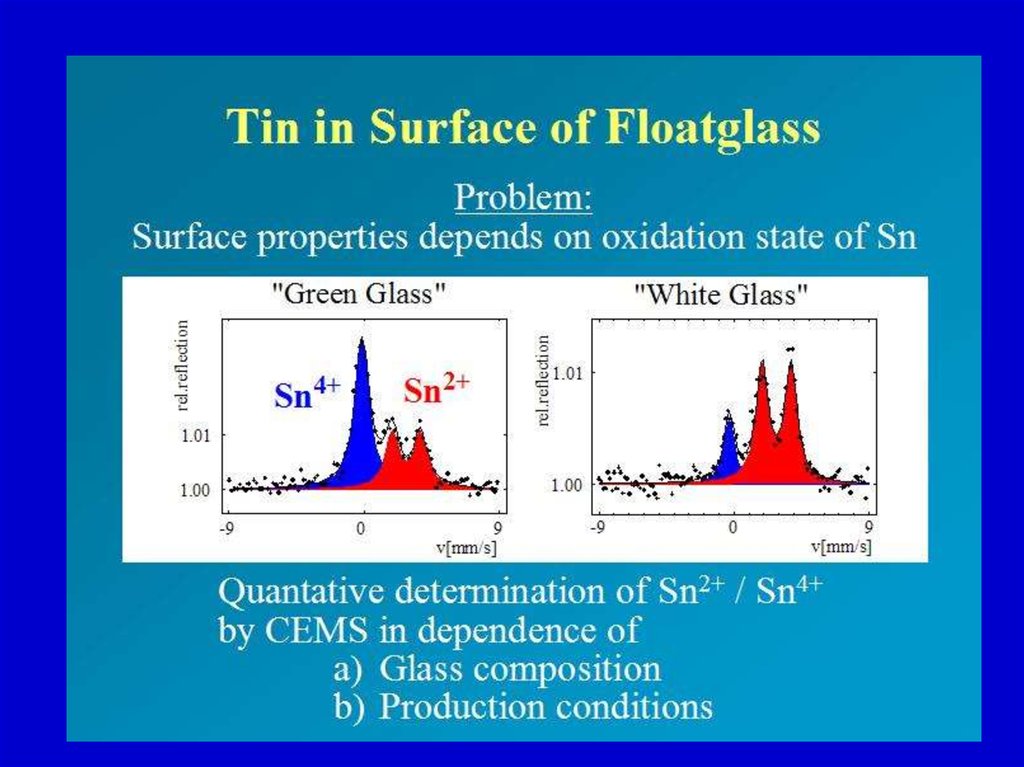
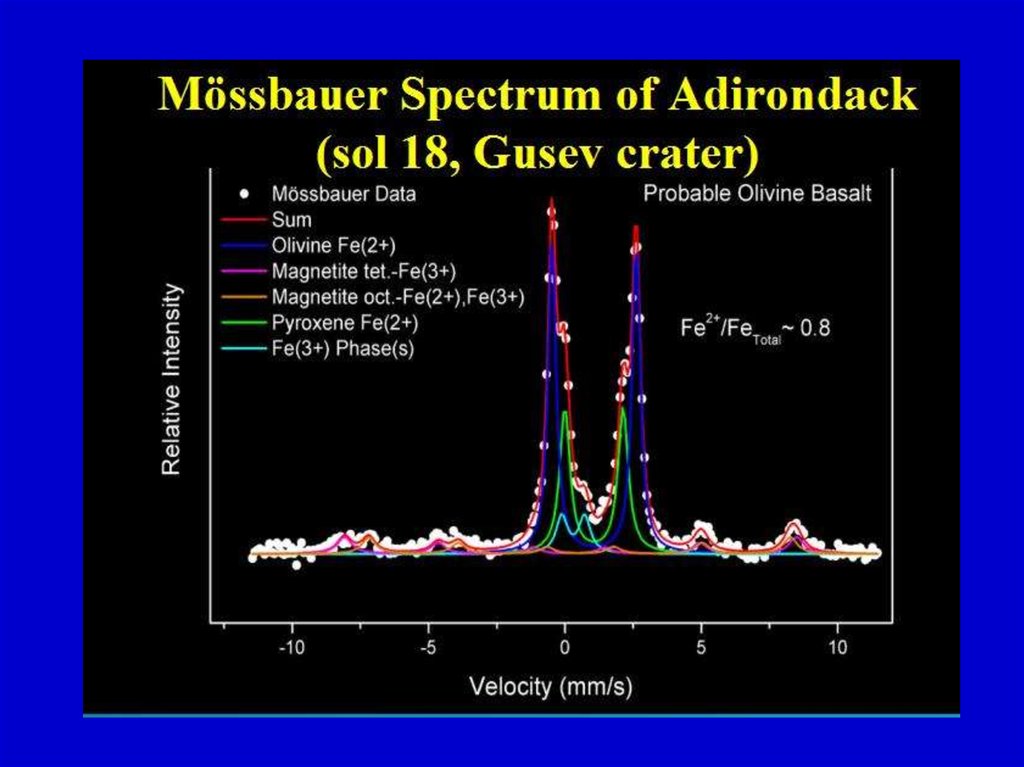
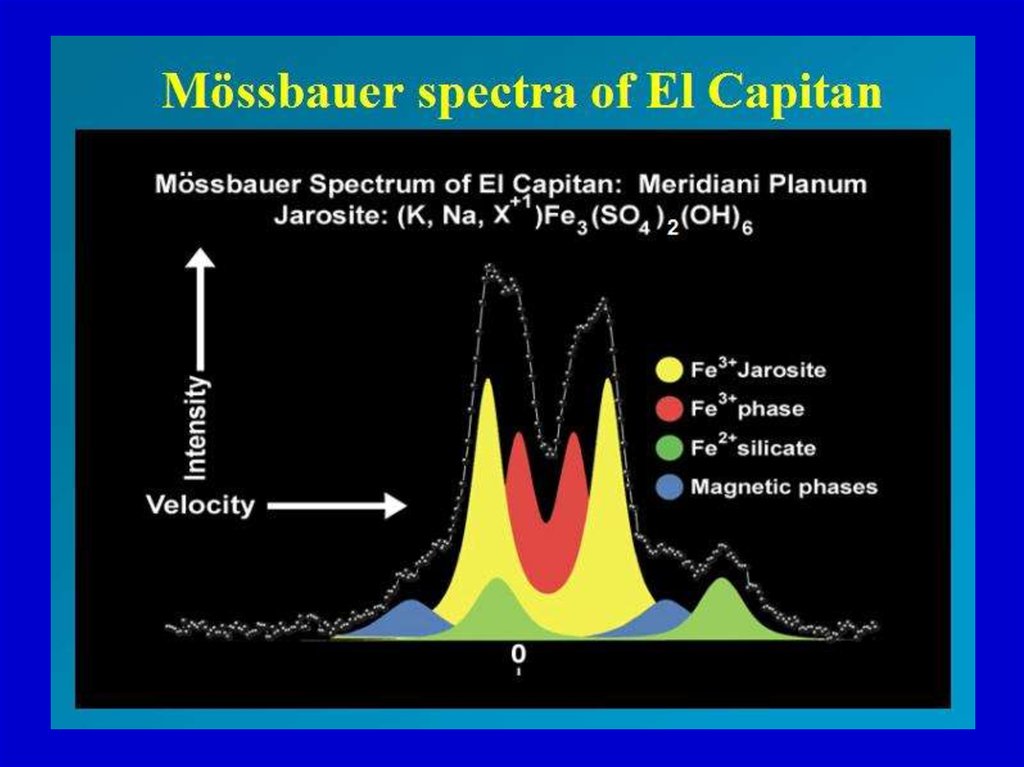
24. Примеры применения Мессбауэровской спектроскопии
25.
26.
27.
28.
29.
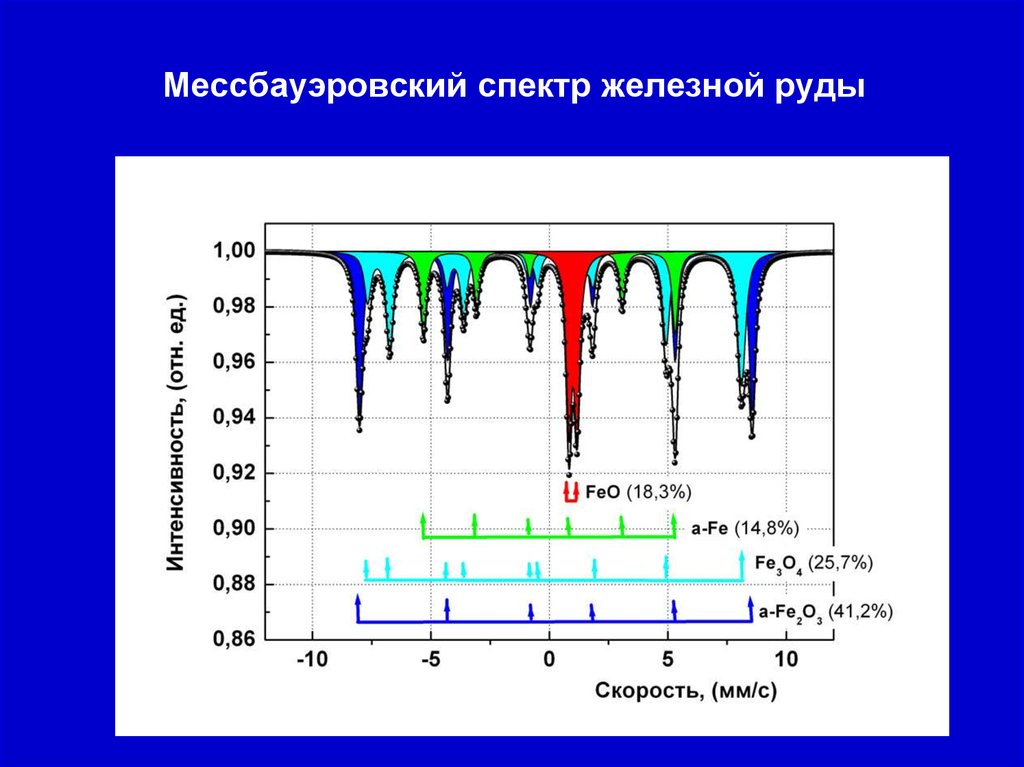
30. Мессбауэровский спектр железной руды
31.
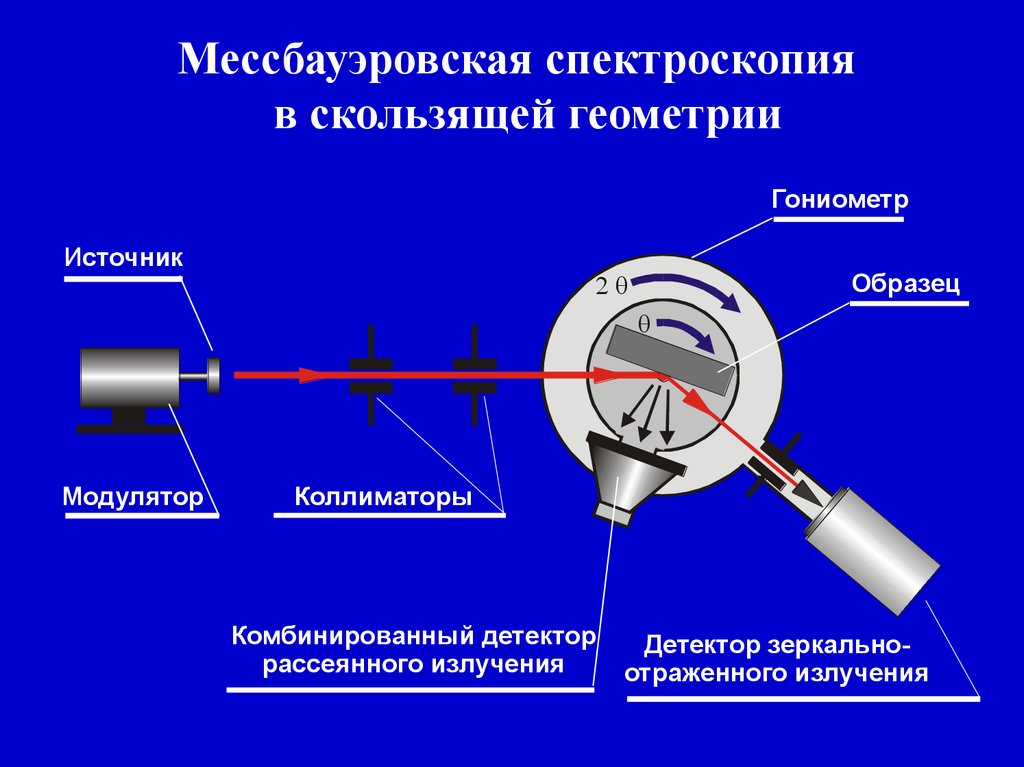
Мессбауэровская спектроскопияв скользящей геометрии
Гониометр
Источник
Образец
Модулятор
Коллиматоры
Комбинированный детектор
рассеянного излучения
Детектор зеркальноотраженного излучения
32.
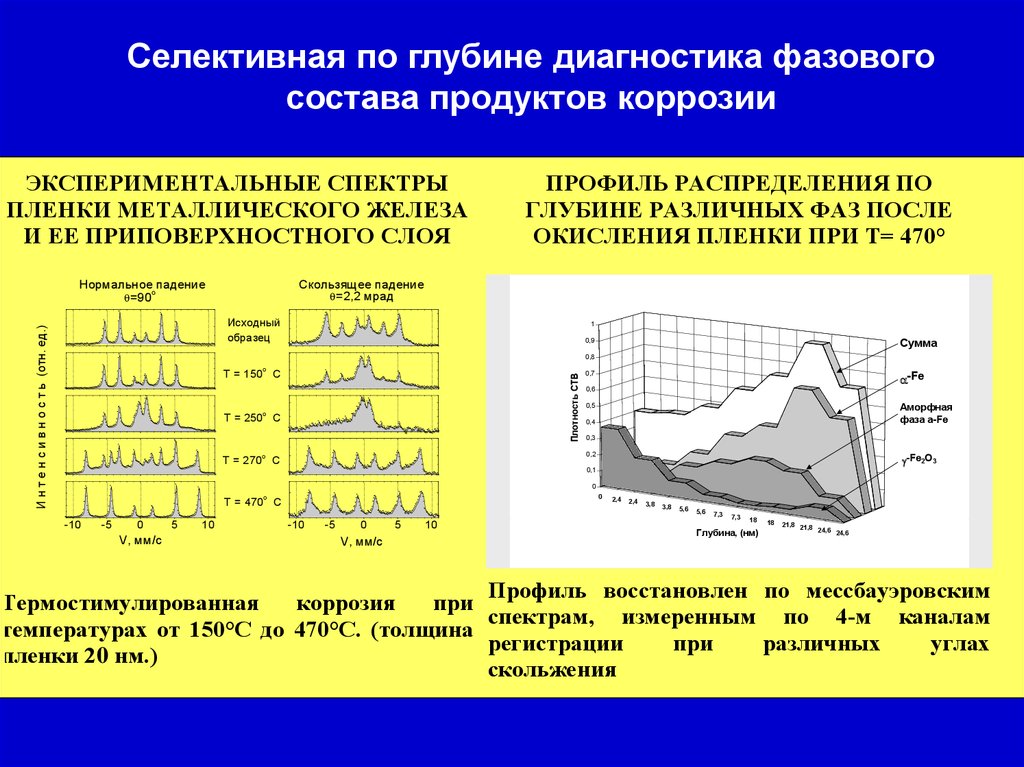
Селективная по глубине диагностика фазовогосостава продуктов коррозии
ЭКСПЕРИМЕНТАЛЬНЫЕ СПЕКТРЫ
ПЛЕНКИ МЕТАЛЛИЧЕСКОГО ЖЕЛЕЗА
И ЕЕ ПРИПОВЕРХНОСТНОГО СЛОЯ
Нормальное падение
o
=90
ПРОФИЛЬ РАСПРЕДЕЛЕНИЯ ПО
ГЛУБИНЕ РАЗЛИЧНЫХ ФАЗ ПОСЛЕ
ОКИСЛЕНИЯ ПЛЕНКИ ПРИ Т= 470°
Скользящее падение
=2,2 мрад
И н т е н с и в н о с т ь (отн. ед.)
Исходный
образец
1
Сумма
0,9
0,8
о
Плотность СТВ
T = 150 С
о
Т = 250 С
0,7
-Fe
0,6
Аморфная
фаза a-Fe
0,5
0,4
0,3
0,2
о
Т = 270 С
-Fe2O3
0,1
0
о
0
T = 470 С
-10
-5
0
V, мм/с
5
10
-10
-5
0
V, мм/с
5
10
2,4
2,4
3,8
3,8
5,6
5,6
7,3
7,3
18
Глубина, (нм)
18
21,8 21,8
24,6 24,6
Профиль восстановлен по мессбауэровским
Термостимулированная
коррозия
при
спектрам, измеренным по 4-м каналам
температурах от 150°С до 470°С. (толщина
регистрации
при
различных
углах
пленки 20 нм.)
скольжения
33.
Динамика сверхтонких взаимодействий и релаксацияСреди методов исследования железосодержащих магнитных
свойств наночастиц, одним из наиболее информативных
является мессбауэровская спектроскопия. В отличие от
магнитных измерений, мессбауэровская спектроскопия может
выявить магнитную динамику наночастиц в частотном диапазоне
107 – 1010 с-1, характерных для мессбауэровского «окна».
Форма
экспериментальных
мессбауэровских
спектров
низкоразмерных объектов сильно усложняется по сравнению со
спектрами для массивных объектов. Причинами этого могут
быть: либо суперпозиция статического набора сверхтонких
структур, обусловленная различием в локальном окружении
резонансных
атомов,
либо
влиянием
различного
рода
динамических процессов (например, диффузия, парамагнитная,
спин-спиновая, спин-решеточная релаксации и т.п.
34. Форма мессбауэровских спектров магнитоупорядоченных материалов
1. Случай хорошо разрешенной сверхтонкой структуры:Ak ( / 2) 2
6
s( )
k 1 (
2
k ) ( / 2)
2
L6 ( H )
2. Случай суперпозиции большого набора сверхтонких структур:
N
s( ) p( H n ) *L6 ( H n )
n 1
3. Случай суперпарамагнитной релаксации:
s( , p, q ) Im
здесь-
o ( )
o ( )
1 6ip o ( )
1
1
1
1
1
1
6 1 2 12/ 2 1/ 2 3 1 2 12/ 2 1/ 2 2 1 2 12/ 2 3 / 2
1 i (4p 2q / 2)
2 i ( 6p / 2 )
p-вероятность переориентации магнитного момента атома на угол /2 между
осями легкого намагничивания, q-вероятность его переворота в единицу времени
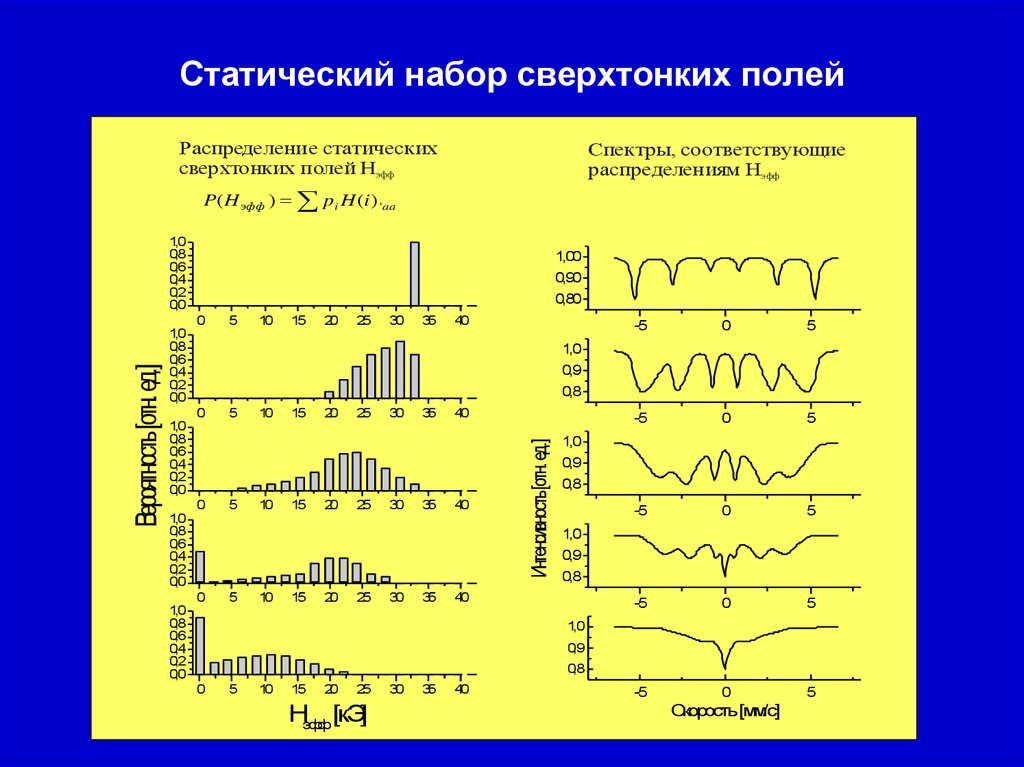
35. Статический набор сверхтонких полей
Распределение статическихсверхтонких полей Hэфф
Спектры, соответствующие
распределениям Нэфф
P (H эфф ) pi H (i ) ' aa
1,0
0,8
0,6
0,4
0,2
0,0
1,00
0,90
0,80
5
10
15
20
25
30
35
40
-5
0
5
-5
0
5
-5
0
5
-5
0
5
0
5
1,0
0,9
0,8
0
5
10
15
20
25
30
35
40
1,0
0,8
0,6
0,4
0,2
0,0
0
5
10
15
20
25
30
35
40
1,0
0,8
0,6
0,4
0,2
0,0
0
5
10
15
20
25
30
35
Интенсивность[отн.ед.]
Вероятность[отн.ед.]
0
1,0
0,8
0,6
0,4
0,2
0,0
1,0
0,9
0,8
1,0
0,9
0,8
40
1,0
0,8
0,6
0,4
0,2
0,0
1,0
0,9
0,8
0
5
10
15
20
25
Нэфф[кЭ]
30
35
40
-5
Скорость[мм/с]
36. Суперпарамагнитная релаксация
1,00,9
0,8
0,7
-10
-5
0
5
10
-10
-5
0
5
10
-10
-5
0
5
10
-10
-5
0
5
10
-10
-5
0
5
10
1,0
0,9
Интенсивность [отн. ед.]
1,00
0,95
0,90
1,00
0,95
0,90
1,00
0,95
0,90
0,85
1,0
0,9
0,8
-15
-10
-5
0
5
10
15
V [мм/с]
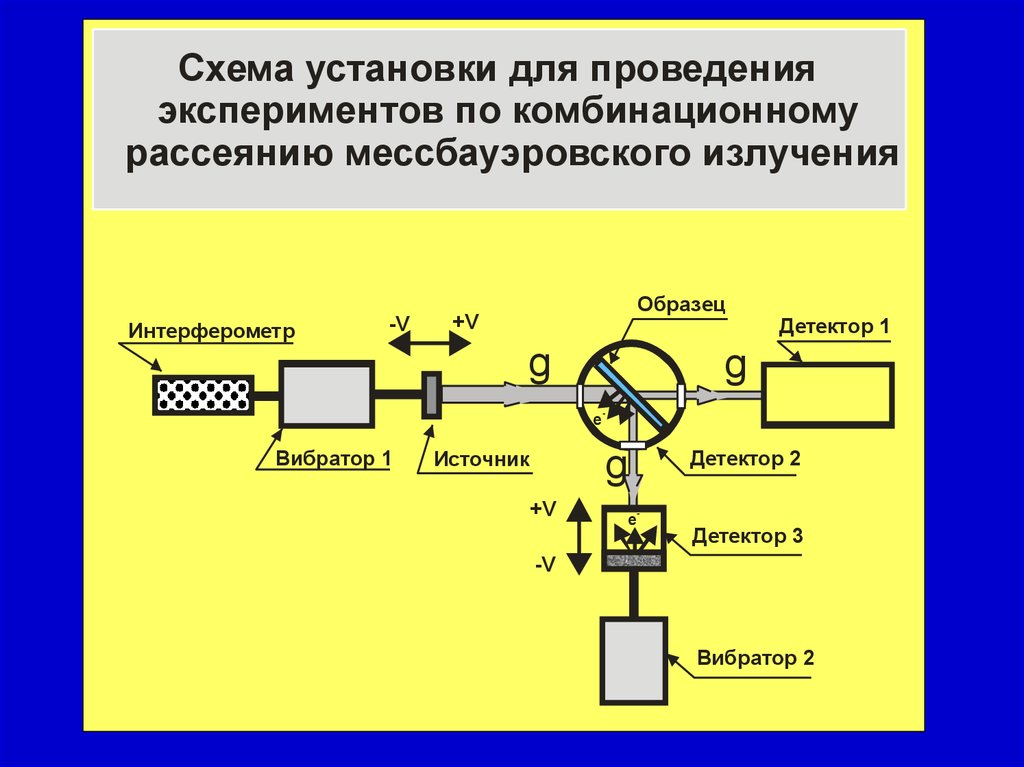
37.
Схема установки для проведенияэкспериментов по комбинационному
рассеянию мессбауэровского излучения
Интерферометр
-V
Образец
+V
g
Детектор 1
g
-
e
Вибратор 1
Источник
Детектор 2
g
+V
e
-
Детектор 3
-V
Вибратор 2
38.
Селективное возбуждение подуровней магнитнойсверхтонкой структуры
а)
в)
Интенсивность [отн. ед.]
5,00
4,00
3,00
2,00
1,00
0,00
-10
б)
-5
0
5
10
V [мм/с]
г)
3,00
Интенсивность [отн. ед.]
Интенсивность [отн. ед.]
6,00
5,00
4,00
3,00
2,00
1,00
1
-10
-5
2
3
4
0
5
2,00
1,00
6
5
10
V [мм/с]
-10
-5
0
5
10
V [мм/с]
а) - схема переходов между ядерными подуровнями основного и возбужденного
состояний -Fe, б) - экспериментальный КЭМ спектр для тонкой пленки -Fe, в)
- энергетический спектр рассеянного излучения при возбуждении уровня -3/2, г) энергетический спектр рассеянного излучения при возбуждении уровня +1/2.
39.
00
0
0
-10
+5
0
-5
Скорость [мм/c]
С
С
С
С
С
0
С
0
С
+10
б)
1,00
Интенсивность [отн. ед.]
0
а)
1,00
0,99
0,98
0,97
0,96
-10
-5
0
5
10
2,00
1,50
1,00
-10
-5
0
5
10
2,00
Интенсивность [отн. ед.]
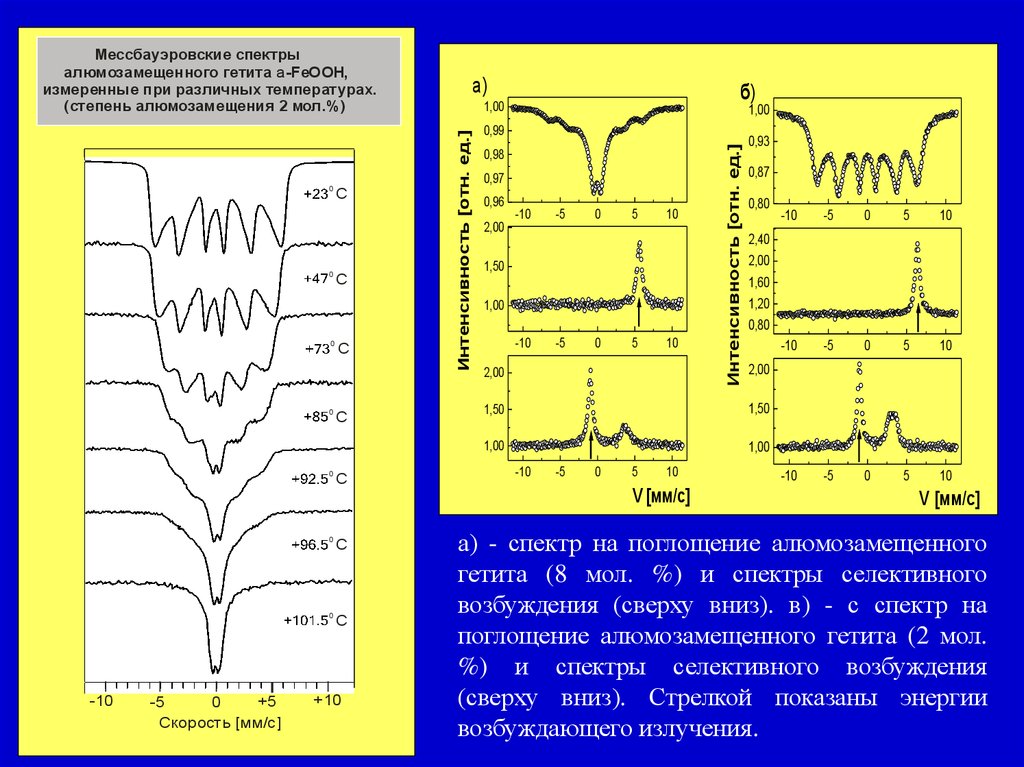
Мессбауэровские спектры
алюмозамещенного гетита a -FeOOH,
измеренные при различных температурах.
(степень алюмозамещения 2 мол.%)
0,93
0,87
0,80
10
V [мм/с]
10
-10
-5
0
5
10
-10
-5
0
5
10
1,20
0,80
2,00
1,00
5
5
1,60
1,00
0
0
2,00
1,50
-5
-5
2,40
1,50
-10
-10
V [мм/с]
а) - спектр на поглощение алюмозамещенного
гетита (8 мол. %) и спектры селективного
возбуждения (сверху вниз). в) - с спектр на
поглощение алюмозамещенного гетита (2 мол.
%) и спектры селективного возбуждения
(сверху вниз). Стрелкой показаны энергии
возбуждающего излучения.
40.
ВОЗБУЖДЕНИЕ ЯДЕРНЫХ РЕЗОНАНСНЫХ УРОВНЕЙСИНХРОТРОННЫМ ИЗЛУЧЕНИЕМ



















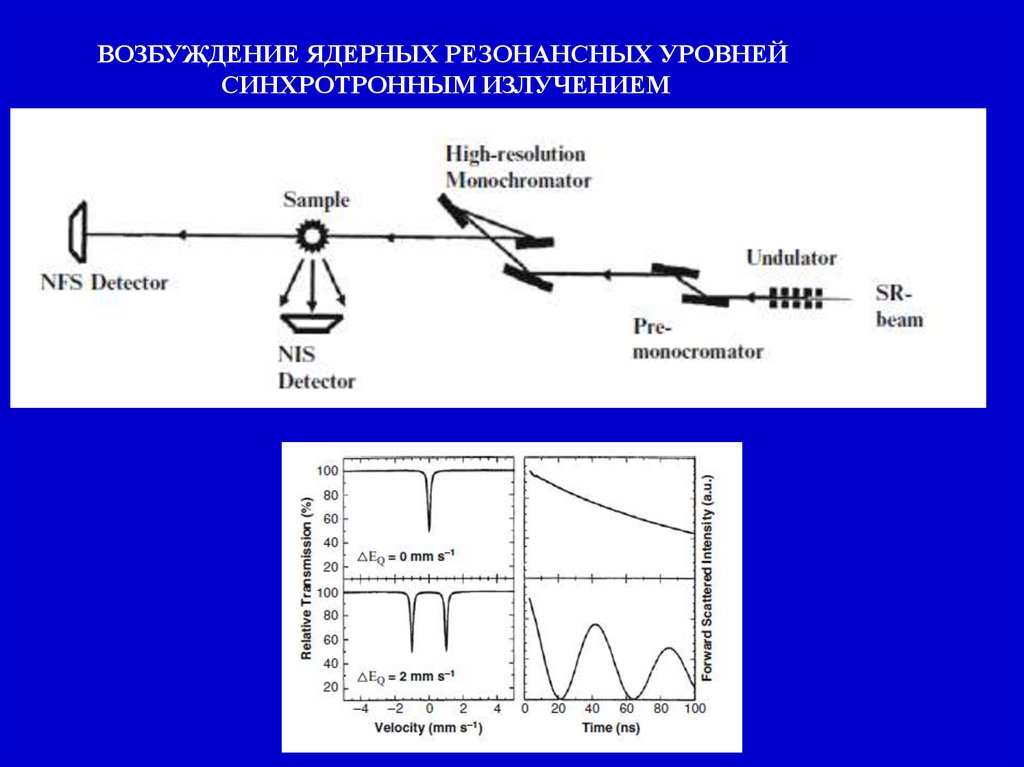

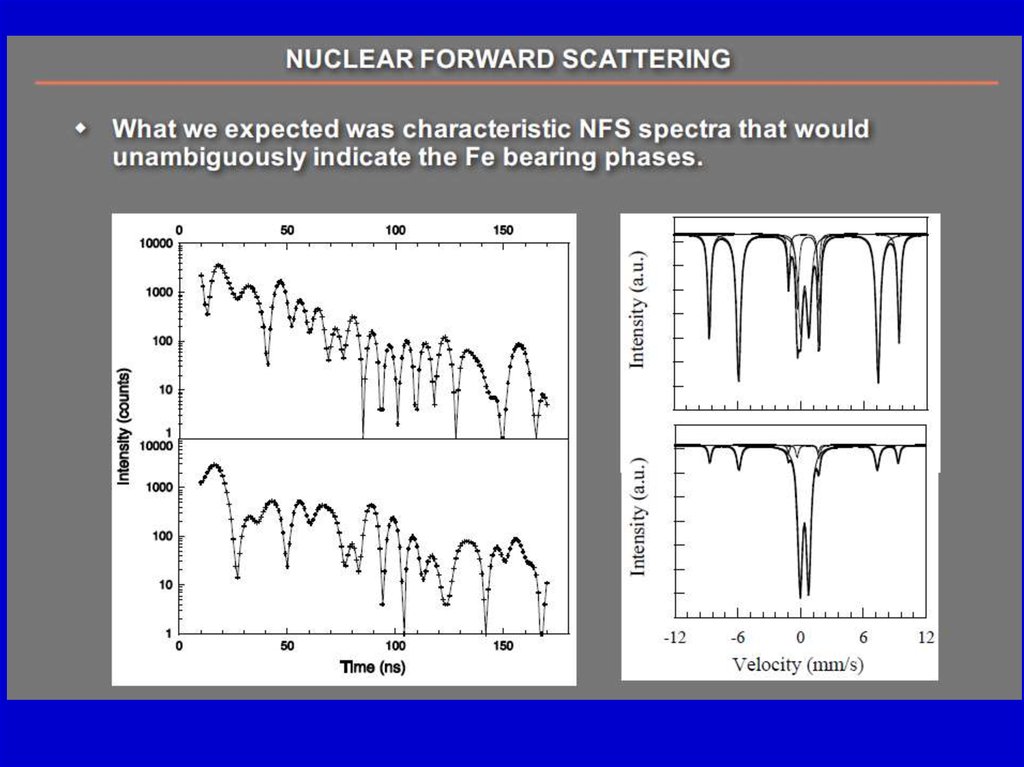

 Физика
Физика








