Похожие презентации:
Elementary interactions: hydrophobic & electrostatic; SS and coordinate bonds
1.
PROTEIN PHYSICSLECTURES 5-6
Elementary interactions:
hydrophobic
&
electrostatic;
SS and coordinate bonds
2.
Hydrophobic effectHenry’s constant
[in gas]
(kH,cc)-1 = [in
liquid]
Concentration of C6H14
in H2O:
50 times less
than in gas!
WHY?
H2O
for
: = 50/1
for ethanol: = 1/47000
3.
ENTROPY:SE = kB • ln[ME];
ME=number_of_states(E)
Why kB? What is kB?
Because entropy SE comes to the free energy
FE = E – TSE (measured in energy units) as TSE,
and T is measured in degrees, while
ln[number of states] is dimensionless;
Thus, kB is energy_unit/degree
FREE ENERGY:
Probability(E) ~ ME•exp(-E/kBT) = exp(-FE/kBT)
Boltzmann
F=E-TS at V=const;
G=H-TS=(E+PV)-TS at P=const (better for experiment)
-------------------
4.
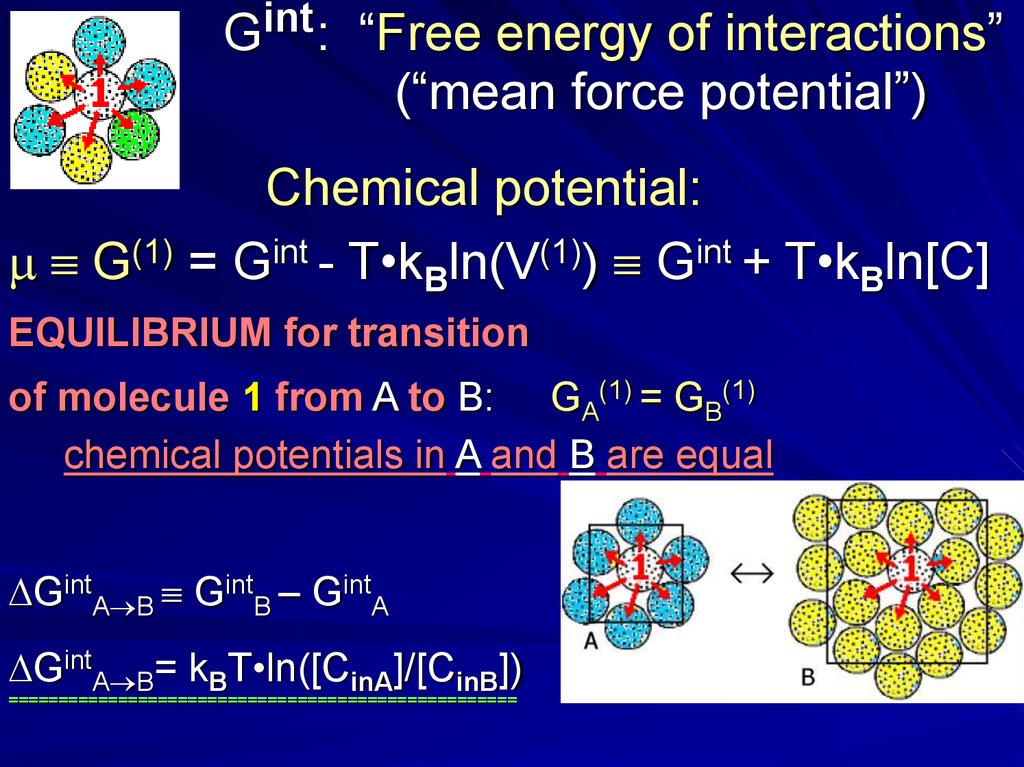
intG :
“Free energy of interactions”
(“mean force potential”)
Chemical potential:
m G(1) = Gint - T•kBln(V(1)) Gint + T•kBln[C]
EQUILIBRIUM for transition
of molecule 1 from A to B: GA(1) = GB(1)
chemical potentials in A and B are equal
GintA B GintB – GintA
GintA B= kBT•ln([CinA]/[CinB])
===================================================
5.
Experiment: G intA B= kBT•ln([C1inA]/[C1inB])SintA B = -d( GintA B)/dT
HintA B = GintA B +T SintA B
C6H12
T=2980K=250C
[C] of C6H12
in H2O:
50 times less
than in gas;
100000 times
less than in
liquid C6H12
6.
Loss: S-2/3
-2/3 +1/3
usual
case
H-bond: directed
Loss:
LARGE E
rare
case
“hydrophobic bond”
7.
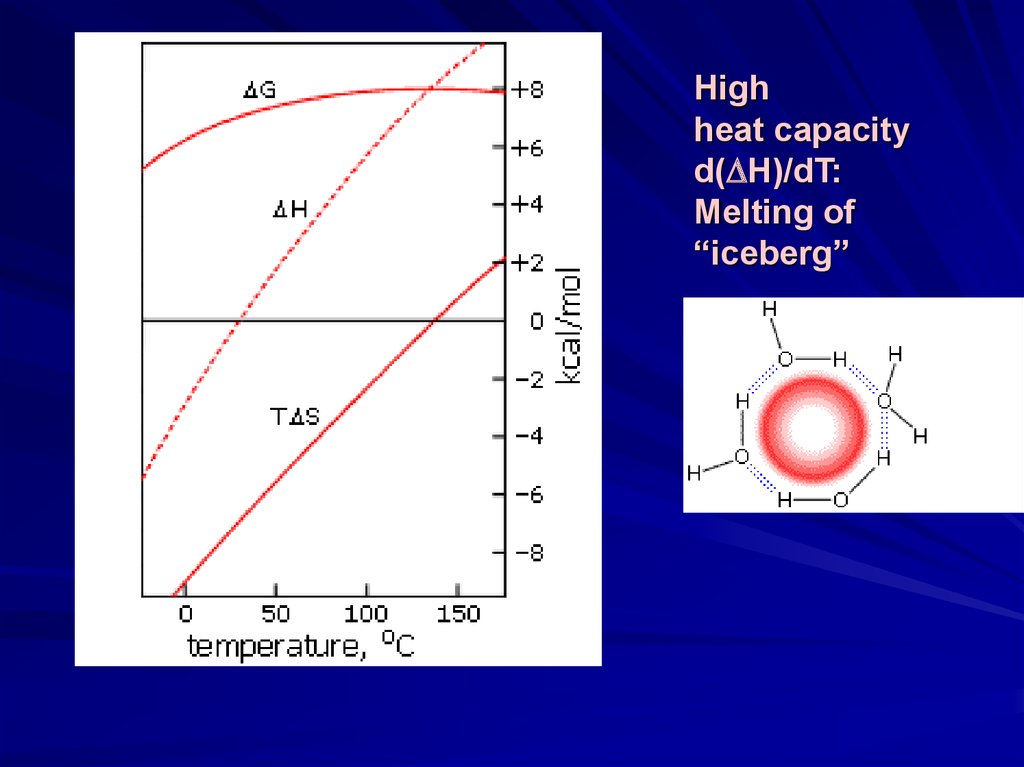
Highheat capacity
d( H)/dT:
Melting of
“iceberg”
8.
Octanol Water20-25 cal/mol per Å2 of molecular
accessible non-polar surface
9.
Hydrophobiceffect
&
denaturation
of proteins
Семён Ефимович Бреслер
(1911 – 1983)
Давид Львович Талмуд
(1900 - 1973)
Hypothesis on a role of hydrophobic effect in protein folding
Charles Tanford
(1921 - 2009)
General physical
features of
Hydrophobic
effect
Cyrus Homi Chothia,
1942
Hydrophobic
effect
&
amino acid
water-accessible
surface
10.
______large
effect
_______
small
______
large
11.
Electrostatics in uniform media:potential 1 = q1/ r
Interaction of two charges:
U = 1q2 = 2q1 = q1q2/ r
= 1 vacuum
3 protein
80 water
Protein/water interface
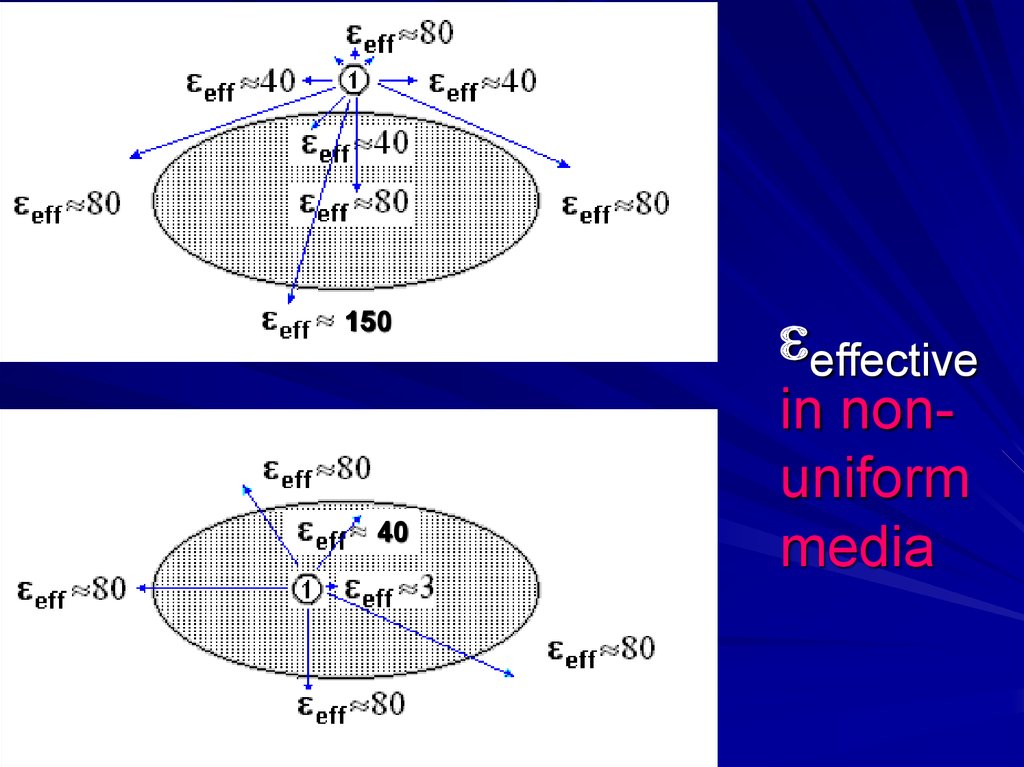
In non-uniform media:
At atomic distances:
eff = ?
eff = ?
12.
(1736-1806)13.
CHARGEinside
PROTEIN
Water => vacuum:
U +100 kcal/mol
Water => PROTEIN
(ε 3)
R 1.5 - 2 Å
U +30 - 40 kcal/mol
CHARGE inside
PROTEIN:
VERY BAD
14.
Non-uniform media:eff = ?
15.
Non-uniform media:eff = ?
16.
Non-uniform media:eff = ?
intermediate dipole
17.
= q/ 1r18.
= (q/ 1)/r- -
19.
= q/r eff in positions:eff≈40
- -
+ -+ - +
–+– + –
Good estimate for
non-uniform media
eff ≈ 150 !!
20.
15040
effective
in nonuniform
media
21.
Large distance:eff = = 80
Atomic distance:
eff = ?
intermediate
“vacuum”, ε~1?
but the absence
of intermediate
dipoles can
only increase
interaction…
22.
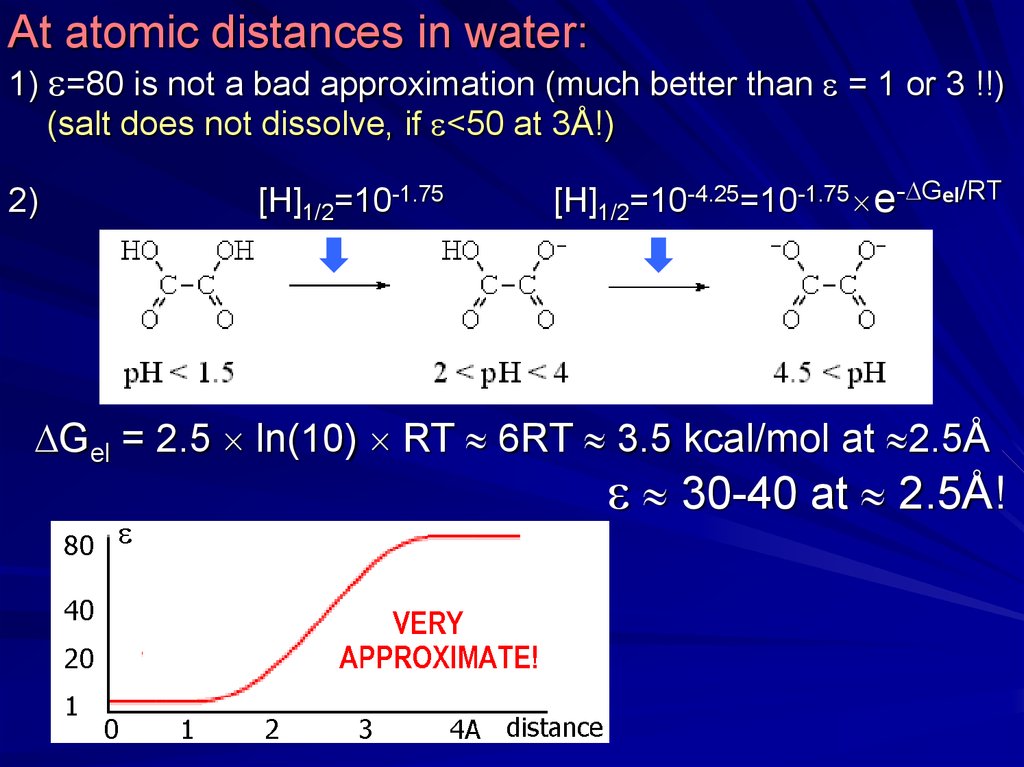
At atomic distances in water:1) =80 is not a bad approximation (much better than = 1 or 3 !!)
(salt does not dissolve, if <50 at 3Å!)
2)
[H]1/2=10-1.75
[H]1/2=10-4.25=10-1.75 e- Gel/RT
Gel = 2.5 ln(10) RT 6RT 3.5 kcal/mol at 2.5Å
30-40 at 2.5Å!
23.
Protein engineering experiments:(r) = pH 2.3RT eff(r)
24.
Sir Alan Roy Fersht, 1943Protein engineering
25.
Dipole interactions(e.g., H-bonds):
Quadruple interactions
(HO)-1/3-H+1/3::::::(OH)-1/3-H+1/3
Also: charge-dipole, dipole-quadruple, etc.
Potentials:
dipole ~ 1/ r2
quadruple ~ 1/ r3
26.
Electrostatic interactions also occur betweencharge (q) and non-charged body, if its 2 differs
from the media’s 1:
U ~ q • [1/ 2 – 1/ 1] • [ 2 /( 1+ 2
4
/2)] • V • (1/r )
at large
In water: repulsion of charges from non-polar
molecules (since here 1>> 2);
in vacuum (where 1< 2) : just the opposite!
1
+
+
+
2
V
-
r
27.
Debye-Hückel screeningof electrostatic by ions:
U = [q1q2/ r]•exp(-r/D) ;
in water: D = 3Å•I-1/2;
Ionic strength I = ½ iCi(Ziion)2 .
Usually: I 0.1 [mol/liter]; D 8Å.
Electrostatics is an example of a multi-body
(charge1, charge2, media, ions) interaction
28.
Electrostatics is T-dependent;U = (1/ )•(q1q2/r)
is free energy (U = H-TS);
TS = T•(-dU/dT) = -T• [d(1/ )/dT]•(q1q2/r) =
= [dln( )/dlnT]•U
in water: when T grows from 273o to 293oK (by 7%),
decreases from 88 to 80 (by 10%):
-TS ≈ 1.3 U; H -0.3U
In water the entropic term (-TS) is the main
for electrostatics!
29.
S-S bonds (Cys-Cys)exchange:
entropic force
S-S bond is not stable
within a cell
30.
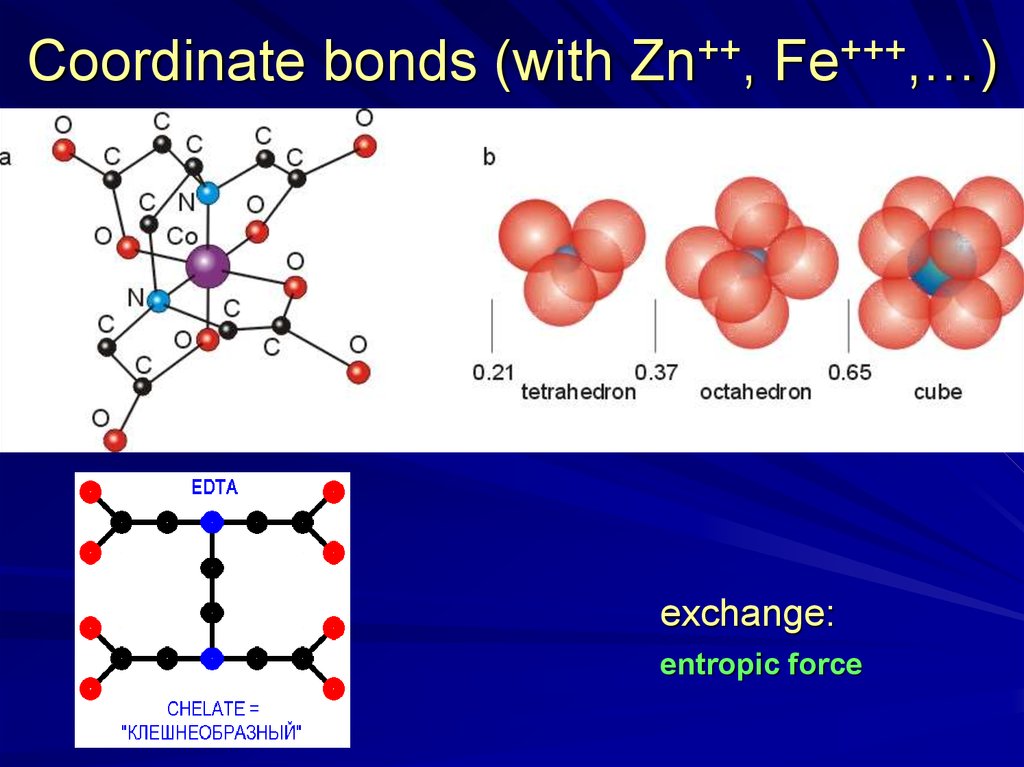
Coordinate bonds (with Zn++, Fe+++,…)exchange:
entropic force

























 Физика
Физика








