Скрещивающиеся прямые

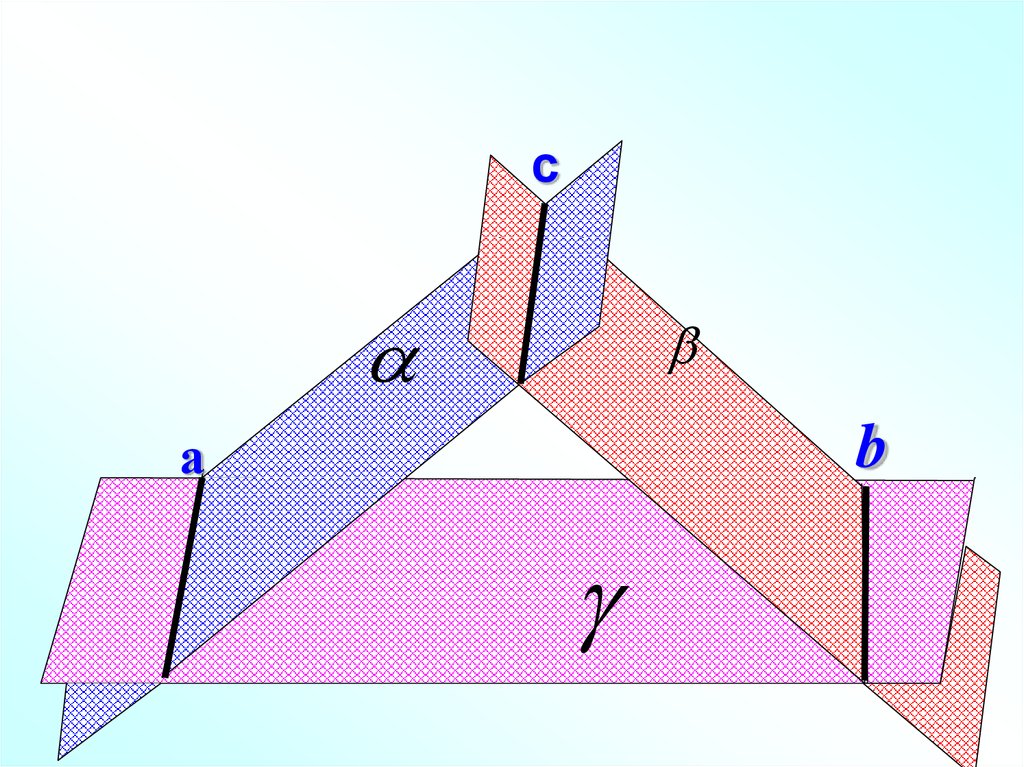
1.

с
b
а

2.

3.

4.

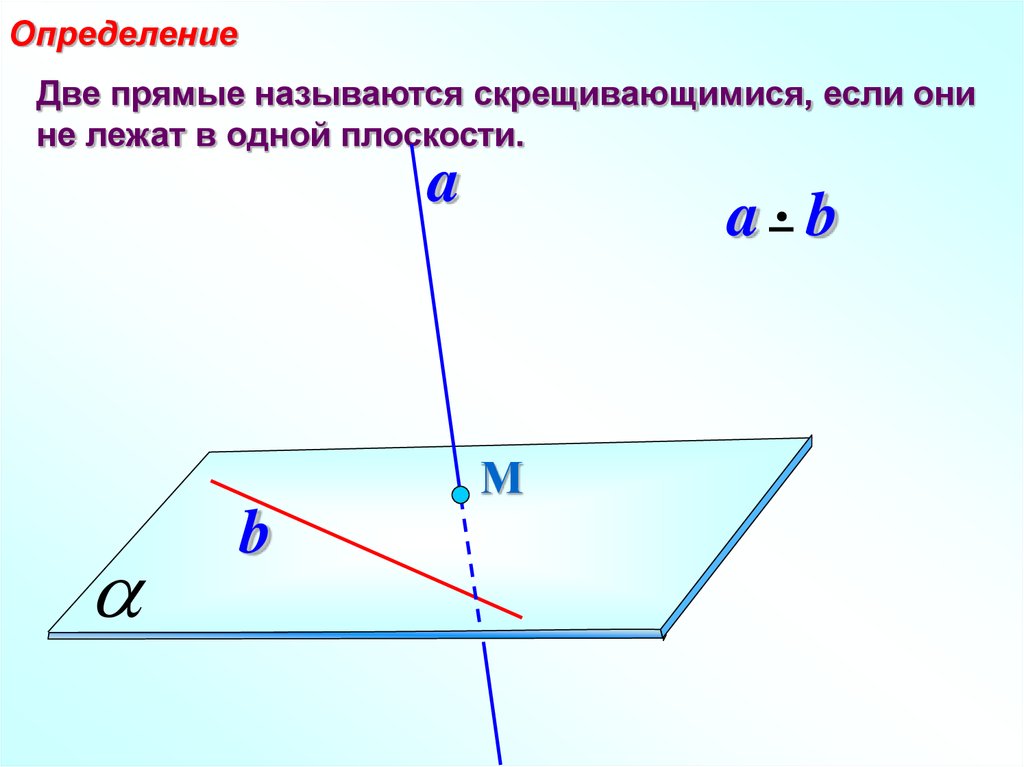
Определение
Две прямые называются скрещивающимися, если они
не лежат в одной плоскости.
a
a b
М
b

5.

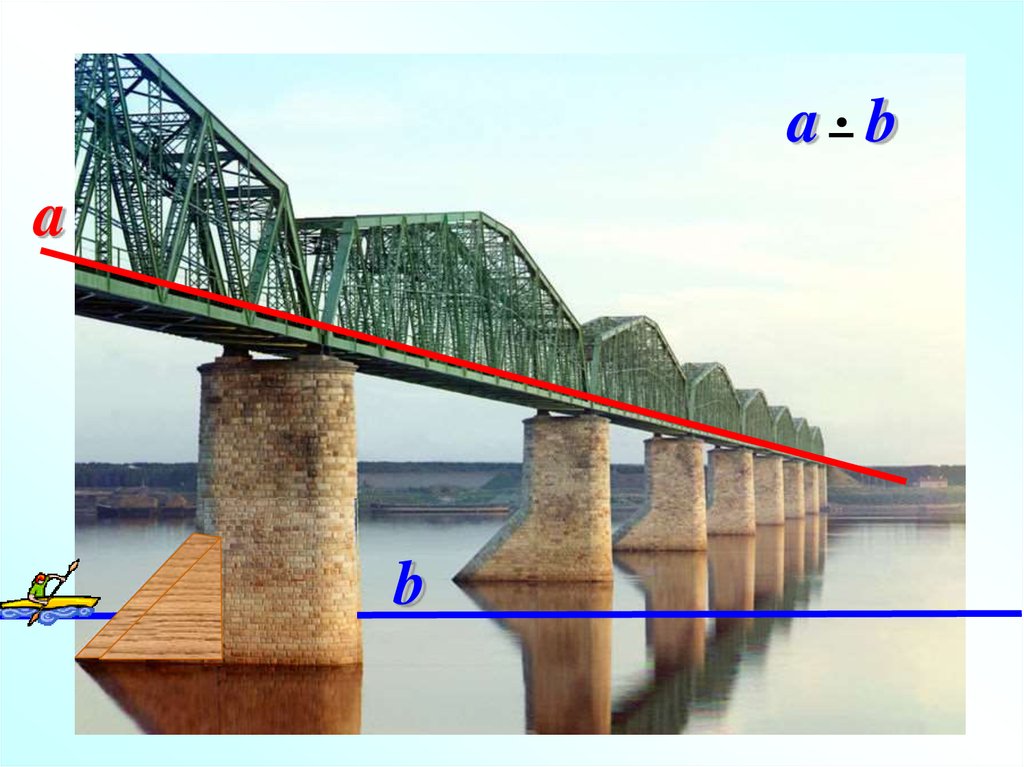
Наглядное представление о скрещивающихся прямых дают
две дороги, одна из которых проходит по эстакаде, а другая
под эстакадой.

6.

a b
a
b

7.

Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

8.

Признак скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости,
а другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые
скрещивающиеся.
D
АВ СD
В
А
C
?

9.

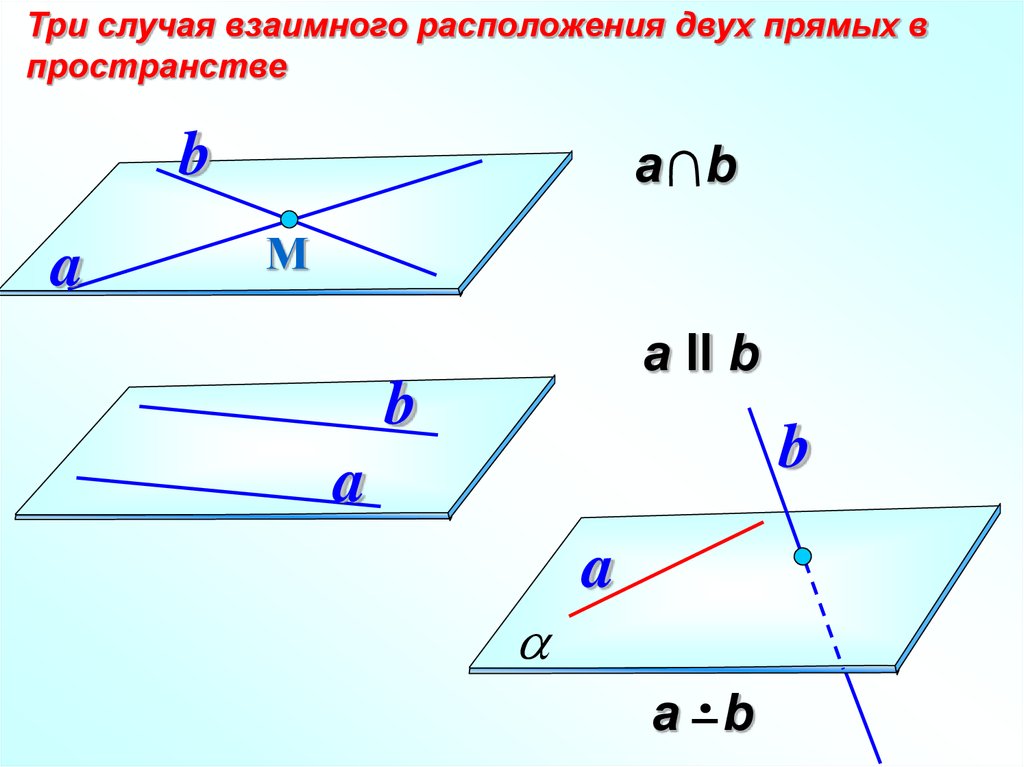
Три случая взаимного расположения двух прямых в
пространстве
b
a
а b
М
а II b
b
b
a
a
а b

10.

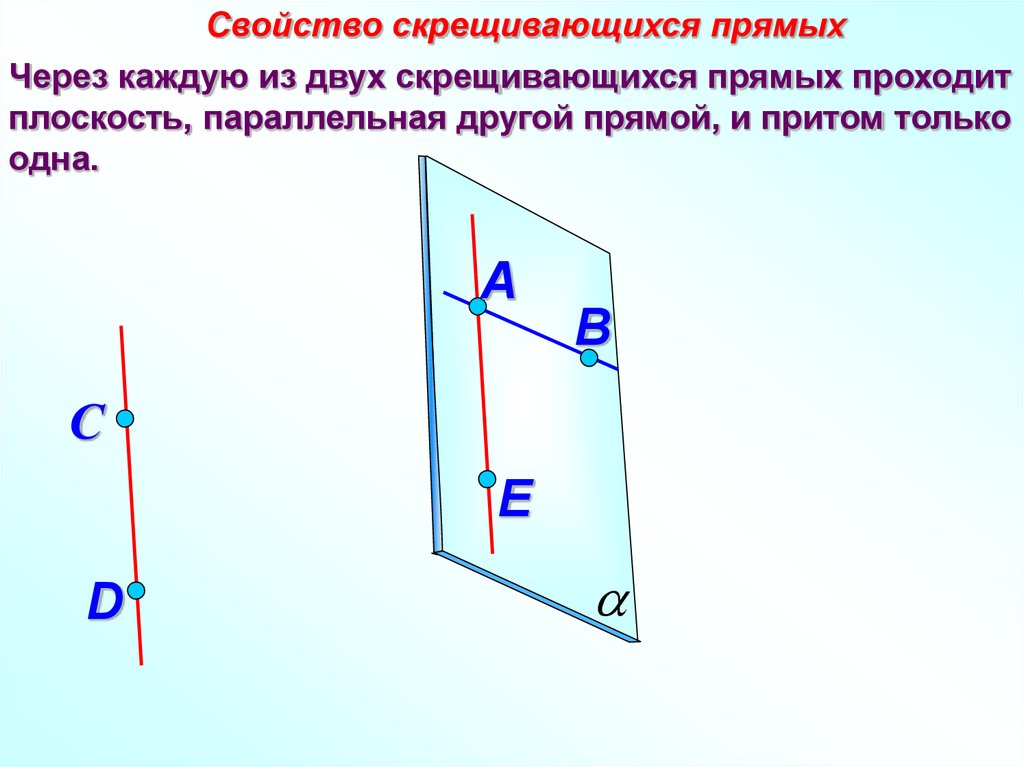
Свойство скрещивающихся прямых
Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только
одна.
A
B
С
E
D

11.

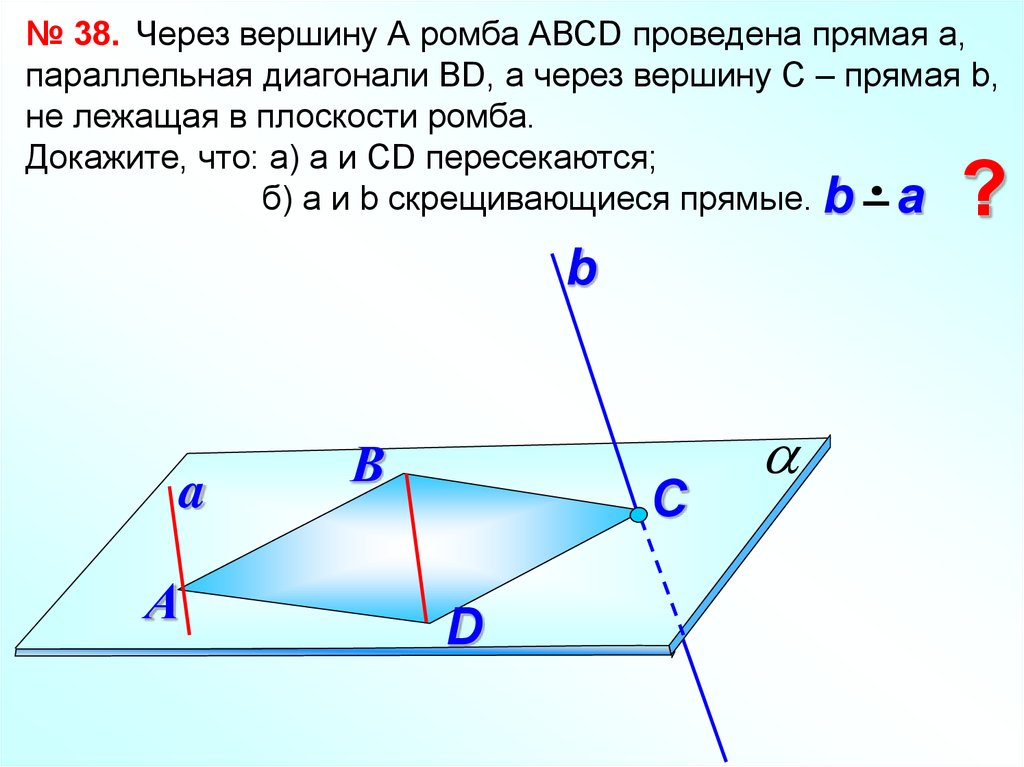
№ 38. Через вершину А ромба АВСD проведена прямая а,
параллельная диагонали ВD, а через вершину С – прямая b,
не лежащая в плоскости ромба.
Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые. b a
?
b
a
А
В
C
D

12.

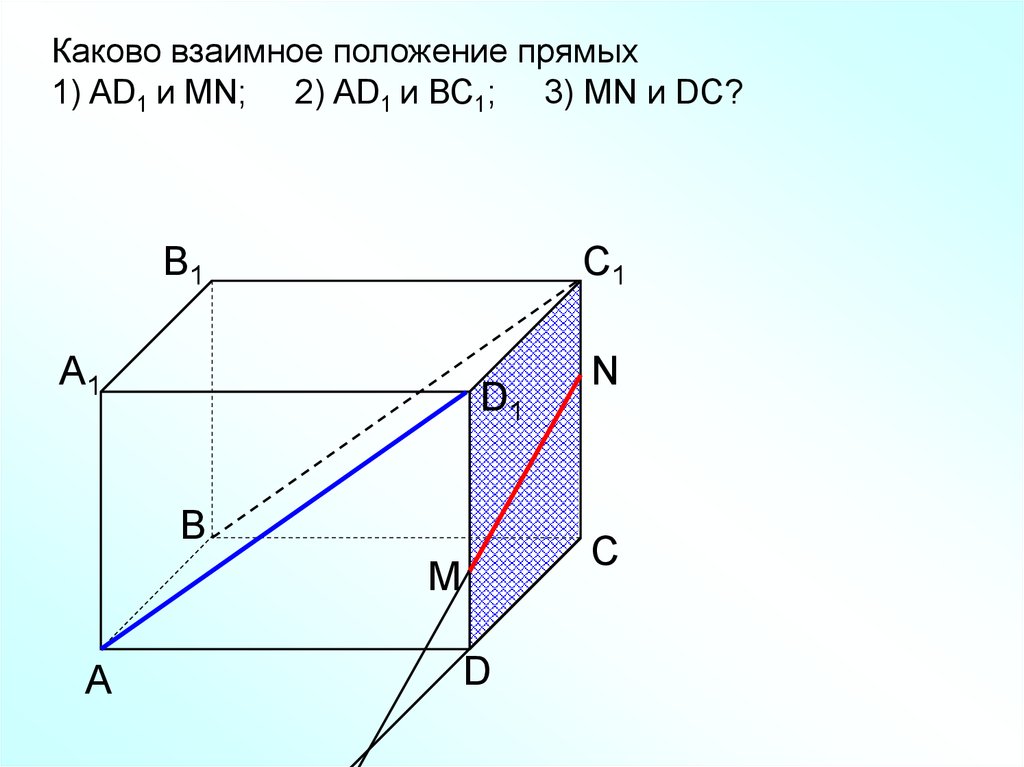
Каково взаимное положение прямых
1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC?
С1
B1
А1
D1
В
С
M
А
N
D

13.

Докажите, что прямые
1) AD и C1D1; 2) A1D и D1C; 3) AB1 и D1C
С1
B1
А1
D1
В
С
M
А
N
D
скрещивающиеся.

14.

Основание призмы АВСDA1B1C1D1 – трапеция.
Какие из следующих пар прямых являются
скрещивающимися?
1) D1C и C1D; 2) C1D и AB1; 3) C1D и AB; 4) AB и CD.
А1
D1
B1
С1
D
А
В
С

15.

Любая прямая а, лежащая в плоскости, разделяет эту
плоскость на две части, называемые полуплоскостями.
Прямая а называется границей каждой из этих
полуплоскостей.
полуплоскость
а
полуплоскость

16.

A3
О3
A2
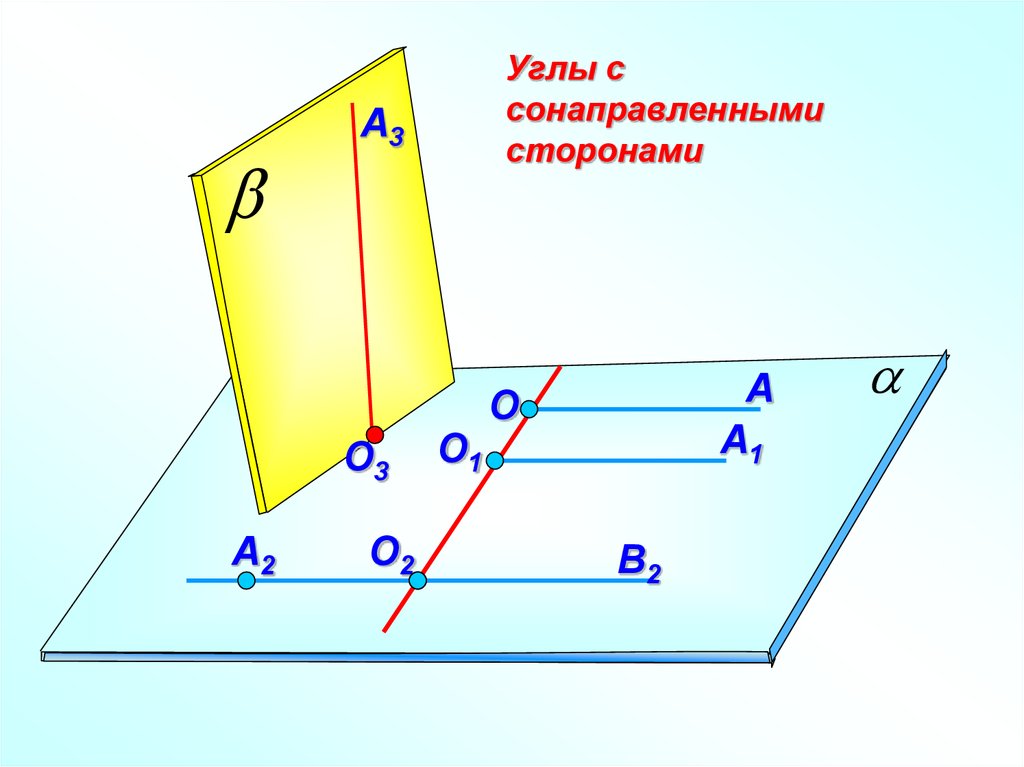
Углы с
сонаправленными
сторонами
О2
О1
A
A1
О
В2

17.

Теорема об углах с сонаправленными сторонами
Если стороны двух углов соответственно сонаправлены,
то такие углы равны.
A
О
B
A1
О1
B1

18.

Угол между прямыми
b
a
180
0
Пусть
- тот из углов, который не превосходит любой из
трех остальных углов. Тогда говорят, что угол между
пересекающимися прямыми равен .

19.

m
n
1000
800
b
300
a
Угол между прямыми а и b
Угол между прямыми m и n
300.
800.

20.

Угол между скрещивающимися прямыми
b
a
n
m
М
а b
Через произвольную точку М1 проведем прямые m и n,
соответственно параллельные прямым a и b.
Угол между скрещивающимися прямыми a и b равен

21.

Угол между скрещивающимися прямыми
b
a
m
М
а b
Точку М можно выбрать произвольным образом.
В качестве точки М удобно взять любую точку на одной из
скрещивающихся прямых.

22.

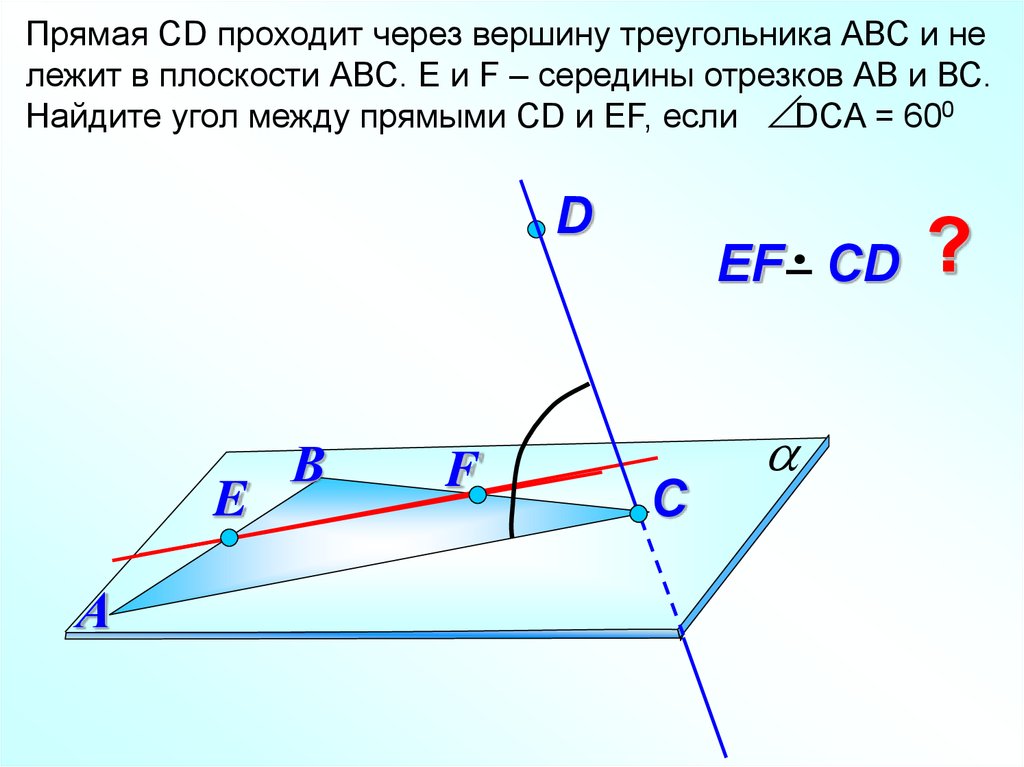
Прямая СD проходит через вершину треугольника АВС и не
лежит в плоскости АВС. E и F – середины отрезков АВ и ВС.
Найдите угол между прямыми СD и EF, если DCA = 600
D
E
А
В
F
EF СD
C
?

23.

Прямая МА проходит через вершину квадрата АВСD и не
лежит плоскости квадрата. Докажите, что МА и ВС –
скрещивающиеся прямые.
Найдите угол между скрещивающимися прямыми МА и ВС,
если МАD =450.
М
B
МА ВС
А
С
D
?

24.

№ 46. Прямая m параллельна диагонали ВD ромба АВСD и не
лежит в плоскости ромба. Докажите, что
а) m и АС – скрещивающиеся прямые – и найдите угол между
ними;
б) m и AD – скрещивающиеся прямые – и найдите угол между
ними, если АВС = 1280.
т
С
В
D
1280
А

25.

На рисунке АВСD – параллелограмм, АВС = 1300,
АА1 II BB1 II CC1 II DD1 и АА1= BB1=CC1=DD1. Найдите
угол между прямыми АВ и А1D1.
Рассмотрите различные способы.
B1
С1
А1
D1
В
С
1300
А
D

26.

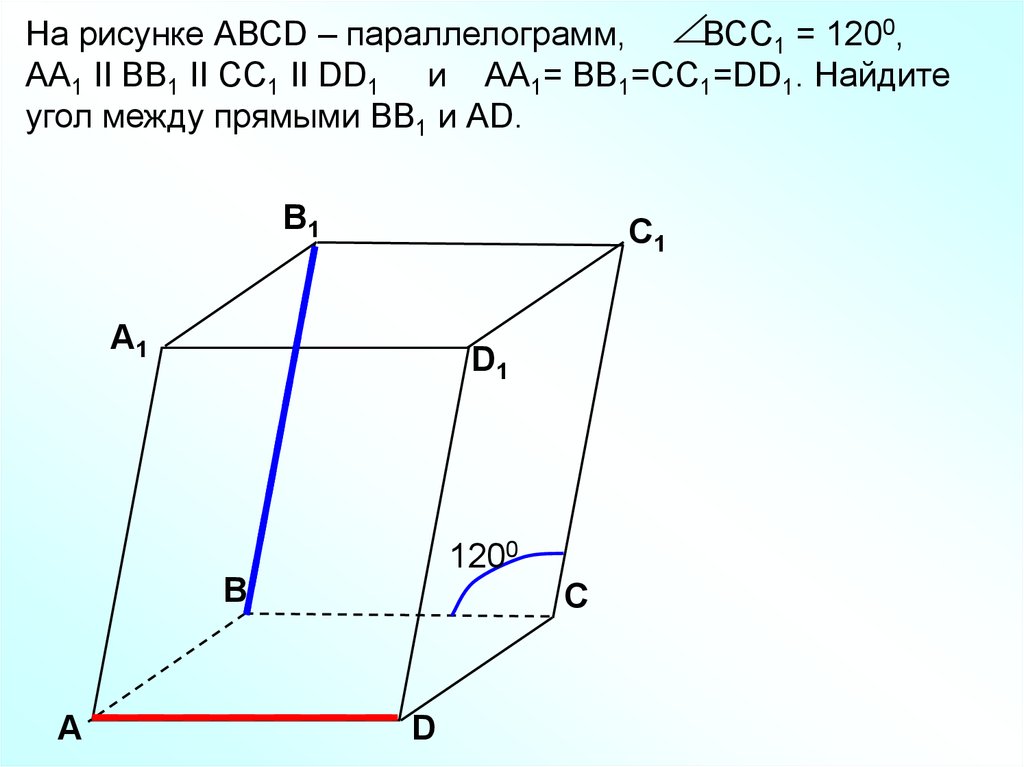
На рисунке АВСD – параллелограмм, ВСC1 = 1200,
АА1 II BB1 II CC1 II DD1 и АА1= BB1=CC1=DD1. Найдите
угол между прямыми ВВ1 и АD.
B1
С1
А1
D1
1200
В
А
С
D