Похожие презентации:
Количественные характеристики случайной величины. Описательная статистика. (Лекция 4)
1. Лекция 4 Количественные характеристики случайной величины. Описательная статистика
2. Вопросы:
1. Меры положения.2. Меры рассеивания признака.
3. Асимметрия и эксцесс.
3. Меры положения
определяют положение центраэмпирического распределения.
- мода;
- медиана;
- среднее арифметическое;
- среднее гармоническое;
- среднее квадратическое;
- среднее кубическое;
- среднее геометрическое;
4. Средняя величина признака
– обобщающий показатель,характеризующий типичный
уровень варьирования изучаемого
признака.
x
I
N
хi – варианты значений признака, N
– объем выборочной совокупности.
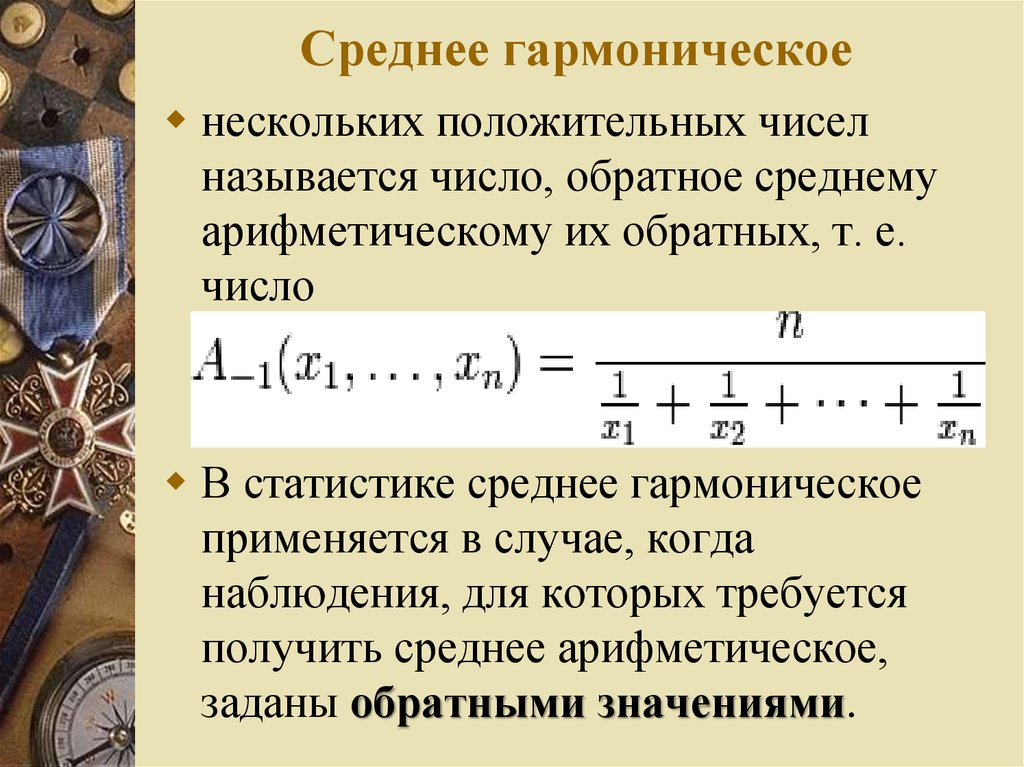
5. Среднее гармоническое
нескольких положительных чиселназывается число, обратное среднему
арифметическому их обратных, т. е.
число
В статистике среднее гармоническое
применяется в случае, когда
наблюдения, для которых требуется
получить среднее арифметическое,
заданы обратными значениями.
6. Медиана
– значение признака, которое лежитв середине ранжируемого ряда и
делит этот ряд на две равные части.
RMe
n 1
2
n – выборочная совокупность.
7. Мода
– наиболее частовстречающееся значение
признака.
8. Графическое представление мер положения
У12
10
8
Х= 11,5
Мо = 10,6
6
Ме = 12,5
4
2
0
0-3
4-7
8-11
12-15
16-19
20-23
9. Меры рассеивания признака
различия индивидуальныхзначений признака у единиц
совокупности.
- размах колебаний,
- среднее линейное отклонение,
- среднее квадратическое
отклонение,
- дисперсия.
10. Причины варьирования признаков
1. Влияние неучтенных признаков (влияниепогодных условий, эмоциональное состояние
испытуемых, мотивация, утомляемость и т.п.)
2. Случайные факторы, обусловливающие
случайное поведение изучаемого признака
(эффект социальной фасилитации).
3. Ошибки измерения, которые
складываются из систематических
погрешностей измерительных приборов,
личных ошибок исследователя (описки,
пропуски, округления и т.п.) и случайных
ошибок измерения.
11. Размах вариации
вычисляется как разность междумаксимальной и минимальной
вариантами выборки
R Х max Х min
Хmax – максимальное значение
признака; Хmin – минимальное
значение признака.
12. Дисперсия
средний квадрат отклонениязначений признака от среднего
арифметическогоS2.
S
2
(Х
i
Xi )
2
n
Хi – значение признака; – среднее
значение признака; n - объем
выборки.
13. Стандартное отклонение (или среднее квадратическое отклонение)
- положительный кореньквадратный из дисперсии
(сгруппированных данных)
S =
(Х
Х) n
2
i
n 1
14. Коэффициент вариации
это выражение в процентахотношения стандартного
отклонения к
среднеарифметическому значению.
Vх
x
100%
где - Х среднее значение признака,
- среднеквадратичное
отклонение.
15. Коэффициент вариации
если коэффициент вариации непревышает 25 %, то выборку
можно считать однородной.
16. Асимметрия
- статистический показатель длясравнительного анализа степени
смещения показателей
распределения признака
относительно среднего значения
A
(x
i
x)
N
3
3
17. Асимметрия
при левосторонней симметриипринимают положительные
значения, а при правосторонней
– отрицательные.
Правосторонняя асимметрия
свидетельствует о том, что
большинство значений
признаков смещено в область
высоких значений и наоборот.
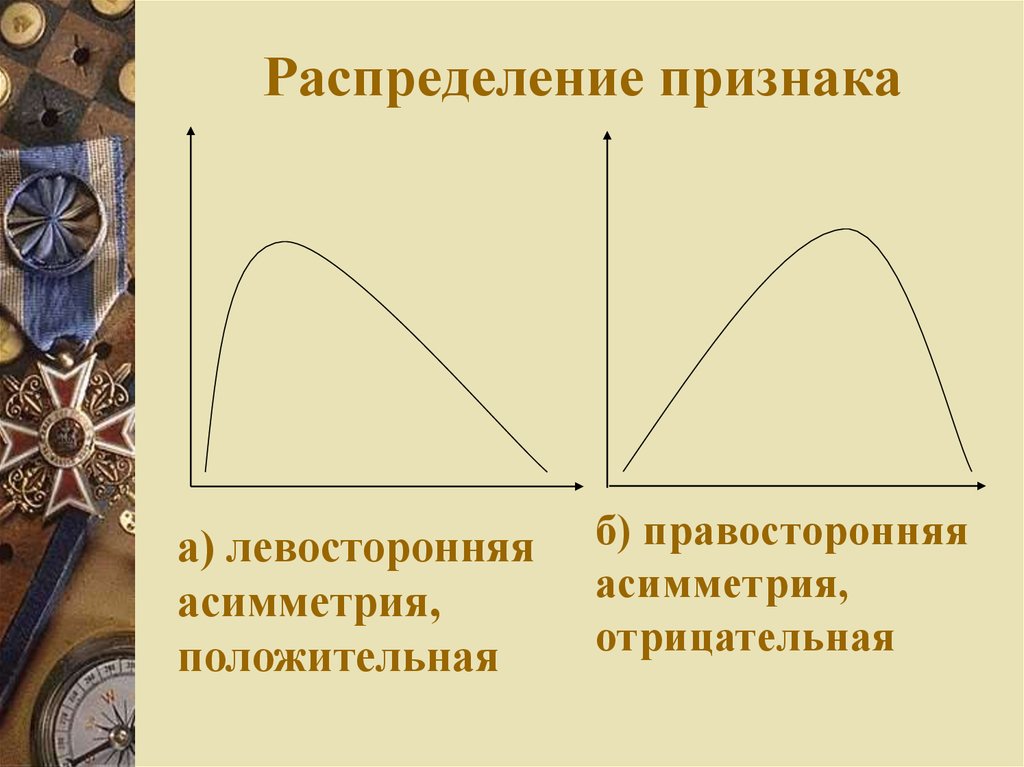
18. Распределение признака
а) левосторонняяасимметрия,
положительная
б) правосторонняя
асимметрия,
отрицательная
19. Коэффициент асимметрии можно рассчитать по формуле Линдберга
Ах МО
20. Эксцесс
– это количественная мера остро иливысоковершинности распределения.
Эксцесс может быть положительным
и отрицательным.
У высоковершинных распределений
показатель эксцесса имеет
положительный знак, а у
низковершинных – отрицательный
знак.
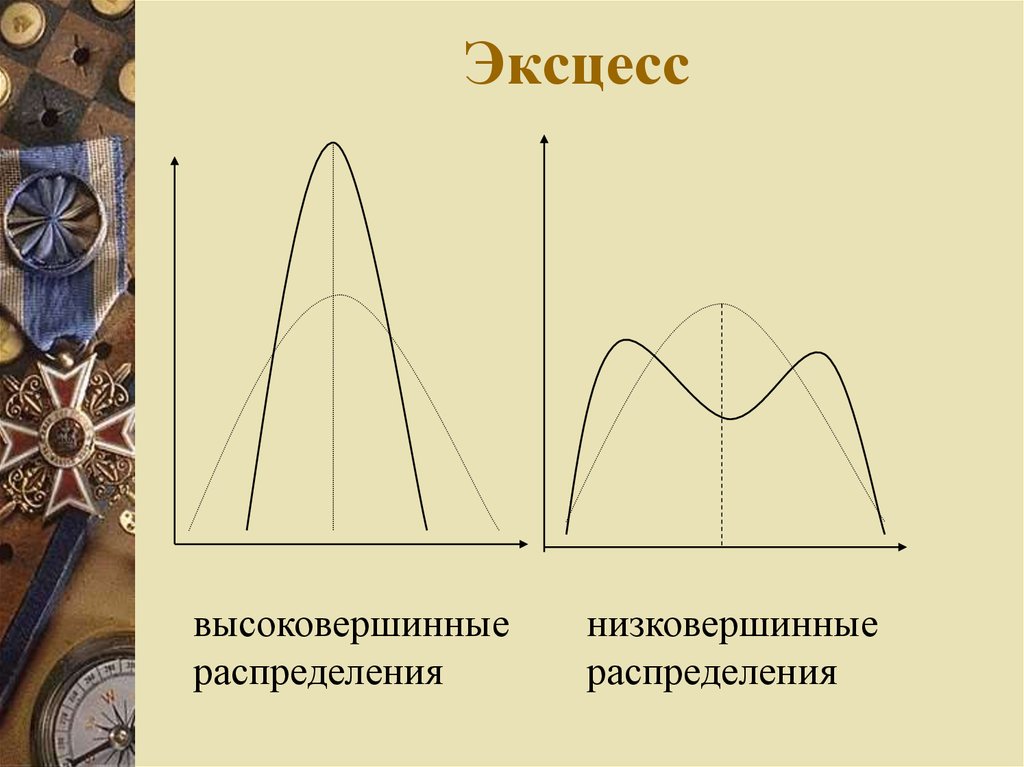
21. Эксцесс
высоковершинныераспределения
низковершинные
распределения
22. Эксцесс
E(
x
x
)
i
N
4
4
3
23. Ошибки репрезентативности
ошибка репрезентативностиасимметрии
mA
n
ошибка репрезентативности эксцесса
mЕ 2
n
24. Условия нормальности распределения (по Пустыльнику Е.И. 1968)
tAAs
3
mA
E
tE
3
mE






















 Математика
Математика Психология
Психология








