Command Shaping for Nonlinear Crane Dynamics

1.

Journal of http://jvc.sagepub.com/
Vibration and Control
Command Shaping for Nonlinear Crane Dynamics
D. Blackburn, W. Singhose, J. Kitchen, V. Patrangenaru, J. Lawrence, Tatsuaki Kamoi and Ayako
Taura
Journal of Vibration and Control 2010 16: 477 originally published online 28 October 2009
DOI: 10.1177/1077546309106142
The online version of this article can be found at:
http://jvc.sagepub.com/content/16/4/477
Published by:
http://www.sagepublications.com
Additional services and information for Journal of Vibration and Control can be found at:
Email Alerts: http://jvc.sagepub.com/cgi/alerts
Subscriptions: http://jvc.sagepub.com/subscriptions
Reprints: http://www.sagepub.com/journalsReprints.nav
Permissions: http://www.sagepub.com/journalsPermissions.nav
Citations: http://jvc.sagepub.com/content/16/4/477.refs.html
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

2.

Command Shaping for Nonlinear Crane Dynamics
D. BLACKBURN
W. SINGHOSE
J. KITCHEN
V. PATRANGENARU
J. LAWRENCE
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332,
USA ([email protected])
TATSUAKI KAMOI
AYAKO TAURA
Tokyo Institute of Technology, Tokyo, Japan
(Received 31 January 20081 accepted 21 March 2008)
Abstract: Motion-induced vibration can be greatly reduced by properly shaping the reference command.
Input shaping is one type of reference shaping method that is based largely on linear superposition. In this
paper we document the impact of nonlinear crane dynamics on the effectiveness of input shaping. As typical
bridge cranes are driven using Cartesian motions, they behave nearly linearly for low- and moderate-velocity
motions. On the other hand, the natural rotational motions of tower cranes make them more nonlinear. The
nonlinear equations of motion for both bridge and tower cranes are presented and experimentally verified
using two portable cranes. The effectiveness of input shaping on the near-linear bridge crane is explained.
Then, a command-shaping algorithm is developed to improve vibration reduction during the more nonlinear
slewing motions of the tower crane. Experimental results demonstrate the effectiveness of the proposed
approach over a wide range of operating conditions.
Keywords: Command shaping, crane control, oscillation, vibration.
1. INTRODUCTION
This paper focuses on the application of input-shaping techniques to reduce commandinduced residual vibration of crane motions. Two types of cranes are investigated, a bridge
crane and a tower crane. Nonlinear equations of motion are presented and then verified using
a portable bridge crane (Lawrence and Singhose, 2005) at the Georgia Institute of Technology and a portable tower crane (Lawrence et al., 2006) at the Tokyo Institute of Technology.
These equations are then linearized and the transition from predominantly linear to substantially nonlinear behavior is documented for the bridge crane. The effectiveness of traditional
Journal of Vibration and Control, 00(0): 1–25, 2009
DOI: 10.1177/1077546309106142
1 2009 SAGE Publications Los Angeles, London, New Delhi, Singapore
1
Figures 2–10, 12–29 appear in color online: http://jvc.sagepub.com
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

3.

2 D. BLACKBURN ET AL.
Figure 1. Input shaping process.
input shaping on bridge cranes is explained, and a novel command-shaping algorithm is
proposed for dealing with nonlinear tower crane dynamics.
Input shaping is a method of command filtering that allows many oscillatory systems to
be moved without inducing residual vibration. Input shaping is implemented by convolving
a series of impulses, known as the input shaper, with a desired reference command. This
produces a command that will drive the system while limiting residual vibration (Smith,
19581 Singer and Seering, 1990). This process is illustrated in Figure 1 with a smooth initial
reference command.
Input shaping is attractive because detailed system knowledge is not necessary1 only
estimates of the natural frequencies and damping ratios of the dominant modes of vibration
are required to design the input shaper. Input shaping relies on the superposition of impulse
responses of a second-order system. To design the input shaper, the response of a secondorder harmonic oscillator of frequency, 1, and damping ratio, 2 , to a series of n impulses is
set equal to zero, or a near-zero value. The equation is then solved to determine the impulse
amplitudes, Ai , and time locations, ti , that would produce such a small value of residual
vibration. This low-vibration impulse sequence is then used in the shaping process shown in
Figure 1.
The earliest form of input shaping was developed by Smith (1958). His posicast control
method replaced a single step input with two step inputs of smaller magnitude, one of which
was delayed by one half-period of vibration. This causes destructive interference in the
responses to each step input and, theoretically, cancels all vibration induced by the two-step
input. This is equivalent to convolving the original step with two impulses. These impulses
are determined by setting the residual vibration to zero. This ensures zero residual vibration
with a perfect model. For this reason, the shaper designed with these constraint equations
is generally referred to as the zero-vibration (ZV) shaper (Smith, 19581 Singer and Seering,
1990).
While the ZV shaper will theoretically yield zero vibration at the modeling frequency, it
is sensitive to modeling errors (Tallman and Smith, 1958). This sensitivity to modeling errors
prohibited the ZV shaper from practical use on many systems. Singer and Seering were
the first to develop an input-shaping technique robust enough to be used in most practical
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

4.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 3
Figure 2. Sensitivity curves for common shapers.
applications. To reduce the sensitivity of the input shaper to errors in natural frequency, they
set the derivative of the vibration with respect to the natural frequency to zero at the modeling
frequency.
The rise-time penalty incurred for the added robustness of this shaper is one extra halfperiod of vibration. As this shaper adds the robustness constraint of zero-derivative at the
modeling frequency, it is called the zero-vibration and -derivative (ZVD) shaper.
The robustness of input shapers can be examined graphically through the use of sensitivity curves. These graphs plot the percentage residual vibration against the normalized
frequency of vibration, 1a 31m , where 1a is the actual system natural frequency and 1m is
the modeling frequency. Figure 2 shows the sensitivity curves for several common shapers.
The solid line corresponds to the ZV shaper, the dashed line corresponds to the ZVD shaper,
and the others correspond to shapers that will soon be described.
In order to increase the robustness of input shapers without adding additional time delays, the requirement of having exactly zero vibration at 1m can be relaxed. If, instead of
forcing the vibration all the way down to zero, it is allowed to equal some small nonzero
value, Vtol , then the shaper can be more robust without incurring an additional rise-time
penalty. This shaper design is known as the extra-insensitive (EI) shaper (Singhose et al.,
1994). This shaper has a hump in its sensitivity curve, as shown in Figure 2.
This idea can be extended to the area of specified-insensitivity (SI) shapers (Singer and
Seering, 19921 Singhose et al., 1996). The insensitivity of a shaper is defined as the width of
the sensitivity curve that lies below a certain vibration threshold. Thus, the 5% insensitivity is
the width of the sensitivity curve that lies below 5% residual vibration. If a certain insensitivity is desired, then the shaper constraint equations can be formulated to attain it. An example
of this shaper is also illustrated in Figure 2 with a 5% insensitivity of 0.7. That is, the vibration is suppressed over a range of frequency ratios from 0.65 to 1.35 (1435 2 0465 3 047).
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

5.

4 D. BLACKBURN ET AL.
1.1. Input Shaping for Multiple Modes of Vibration
There are also ways to use input shaping to reduce vibration in multiple modes. One way
is to design shapers for each individual mode and then convolve them together (Hyde and
Seering, 19911 Singhose et al., 1997b). The resulting shaper will provide vibration reduction
at the desired frequencies, with added robustness for higher mode excitation. Another way
to design the shaper is to solve the constraint equations for the two modes simultaneously
(Hyde and Seering, 19911 Singhose et al., 2008). This method results in vibration reduction
near the modeling frequencies, but does not yield as much suppression of the high modes.
However, a simultaneous shaper is often significantly shorter than a convolved shaper. This
advantage in speed can be important for slow oscillations, such as those occurring in crane
payloads (Singhose et al., 1997b).
1.2. Applications of Input Shaping
Input shaping can be very helpful for reducing vibration in a wide variety of mechanical systems. Two systems of special note mentioned here are cranes and flexible spacecraft. Both
cranes and flexible spacecraft often oscillate with long periods and have little damping. Consequently, numerous feedback control methods have been developed for such systems (Masoud et al., 20031 Abdel-Rahman et al., 20031 Sorensen et al., 2007, 2008). However, input
shaping can be extremely useful in reducing command-induced vibrations and increasing the
speed and accuracy of these systems without the need for sensors and feedback controllers.
Input shaping was first implemented on a gantry crane at the Savannah River Technology
Center (Singer et al., 1997). Fixed-duration (FD) shapers were implemented on this crane, in
which the shaper duration was held fixed while the robustness to modeling errors was maximized. This process creates a set of shapers for different payload suspension lengths with
identical rise times. Constant rise times are desirable from an operator standpoint, as they
do not have to adjust for variable deceleration times. Smith et al. (2004) applied robust input shaping to trajectory tracking of payloads suspended from multiple robot manipulators.
Hong and Hong (2004) showed simulation results for point-to-point motions of container
cranes using a deflection-limiting input shaping technique and nonlinear vibration stabilization control.
Input shaping has also been studied extensively for applications to flexible spacecraft.
Input shaping was used to develop fuel-efficient pulse profiles for the slewing of flexible
spacecraft with on–off reaction jets. Robustness commands were used to perform fuelefficient slewing of flexible spacecraft, while also limiting transient deflection (Singhose
et al., 1997a). Hu and Ma (2005) applied a technique similar to input shaping called component synthesis vibration suppression (CSVS) combined with positive position feedback
(PPF) piezoelectric sensing and actuation to suppress vibration of a slewing spacecraft with
on–off thrusters. Robust shaping was also applied to the problem of momentum dumping of
spacecraft reaction wheels (Banerjee et al., 2001).
Watanabe et al. (2004) applied input shaping to electrodynamic tether operations. Two
cases of satellite deorbit and one case of International Space Station reboost were considered
in the investigation. Input shaping was shown to drastically reduce tether libration and string
vibration during the maneuvers. Robustness of the control system to variations in system
parameters was also demonstrated.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

6.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 5
Figure 3. Bridge crane diagram.
Figure 4. Portable bridge crane.
2. BRIDGE CRANE
2.1. System Model
An illustration of a bridge crane is shown in Figure 3. A picture of the portable bridge
crane used for experiments is shown in Figure 4. The trolley slides along the bridge in the
x direction, and the bridge moves along the runway in the y direction. Thus, the trolley
naturally operates in a Cartesian space. If the suspension length, L, is held constant, then
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

7.

6 D. BLACKBURN ET AL.
the equations of motion relating the payload swing angles, 5 and 6, to the acceleration of the
trolley in the x and y directions are (Blackburn et al., 2006):
L 54 5 L 66 cos 758 sin 758 5 g sin 758 cos 768 3 x4 cos 758 5 y4 sin 758 sin 768
2
L 64 cos 758 2 2L 56 66 sin 758 5 g sin 758 3 2 y4 cos 76 8 4
(1)
These equations can be converted into nonlinear state space equations of the form
x6 3 f 7x9 u8
where
x 3
u 3
1
5 56 6
1
x4
y4
2T
66
x
(2)
x6
y6
y
2T
4
(3)
This yields the following state space equations:
x61 3 x 2
x62 3 2x42 cos 7x1 8 sin 7x 1 8 2
g
1
1
sin 7x1 8 cos 7x3 8 5 u 1 cos 7x 1 8 5 u 2 sin 7x1 8 sin 7x 3 8
L
L
L
x63 3 x 4
x64 3 2x 2 x4 tan 7x1 8 2
g sin 7x 3 8
1 cos 7x3 8
2 u2
L cos 7x1 8 L cos 7x1 8
x65 3 x 6
x66 3 u 1
x67 3 x 8
x68 3 u 2 4
(4)
In order to obtain a linear model of the system, the system can be linearized about x 3 u 3 0
according to the following formula:
3
f
1
4
x1
4
4
f
4 2
4
4
A 3 4
x1
4 4
4 44
4
4
5
fn
x1
f1
x2
777
f2
x2
44
777
4
777
f1 6
xn 7
7
44 7
7
4 7
7
7
44 7
4 7
7
7
fn 8
xn
x30
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

8.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 7
3
f1
u 2
f1
4
u 1
4
4
4
f2
4
4
u 1
4
B34
4 44
4 4
4
4
4
fn
5
u 1
777
f2
u 2
44
4
777
6
f1
u m 7
7
7
44 7
4 7
7
7
7
7
7
7
7
fn 7
8
u m
(5)
u30
to obtain the following linear state space equation:
x6 3 Ax 5 Bu
(6)
where
3
0
4
4 g
42
4 L
4
4
4 0
4
4
4 0
4
A 3 4
4
4 0
4
4
4
4 0
4
4
4 0
5
0
3
0
4
41
4
4L
4
4
40
4
4
4
40
B 3 4
4
4
40
4
4
41
4
4
4
40
5
0
1
0
0
0
0
0
0 2
0
g
L
0
0
0
0
0
0
0
6
0
6
0 0 0 0 0
7
7
0 0 0 0 07
7
7
7
1 0 0 0 07
7
7
0 0 0 0 07
7
7
7
0 0 1 0 07
7
7
7
0 0 0 0 07
7
7
0 0 0 0 17
8
0 0 0 0 0
7
7
07
7
7
7
07
7
7
17
7
L7
74
7
07
7
7
07
7
7
7
07
8
1
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011
(7)

9.

8 D. BLACKBURN ET AL.
Figure 5. Experimental and nonlinearly simulated payload trajectories.
The payload position is given by
xpayload 3 x 2 L sin 758
ypayload 3 y 5 L cos 758 sin 768 4
(8)
2.2. Model Verification
The portable bridge crane used for experimental verification is approximately 1 m 8 1 m 8
146 m in size. It is driven by two Siemens synchronous AC servo motors that move the
trolley and bridge axes via timing belts, allowing movement in the x and y directions. A
Siemens digital camera is attached to the trolley to measure the payload swing, and a Siemens
programmable logic controller (PLC) is used to generate the velocity commands. These
commands are sent to the motor drives which use encoders for proportional-plus-integral
(PI) velocity feedback control (Lawrence and Singhose, 2005).
Under normal operation, the payload swing angles are fairly small, thereby causing
bridge cranes to behave in a linear manner. Figure 5 shows an overhead view of the nonlinearly simulated and measured crane payload responses to a typical two-axis move, while
Figure 6 shows the linearly simulated response. Comparing Figures 5 and 6 shows that
the nonlinear and linear models have nearly identical responses for small payload swing
angles.
To expose the model differences and to verify the nonlinear equations of motion, a trajectory that induces large swing angles and velocities was used to drive both the numerical
simulations and the portable bridge crane. The trolley was driven rapidly to induce large
swing angles. Then, at the approximate time of maximum swing on one axis, the crane was
driven in the transverse direction. Figure 7 shows fairly good agreement between the experimental data and the nonlinear simulation for this case. The response of the linear model is
compared with the experimental response in Figure 8. A significant difference between the
two models is apparent in the coupling between the two swing angles. This is evident in the
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

10.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 9
Figure 6. Experimental and linearly simulated payload trajectories.
Figure 7. Experimental and nonlinearly simulated payload trajectories.
Figure 8. Experimental and linearly simulated payload trajectories.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

11.

10 D. BLACKBURN ET AL.
Figure 9. Experimental and simulated trolley swing angle (5 ).
Figure 10. Experimental and simulated bridge swing angle (6 ).
“swirling” effect seen in the experimental and nonlinear data, but which is absent from the
linear model.
Further comparison can be made by graphing the payload swing angles individually.
These profiles can be seen in Figures 9 and 10. The linear model predicts a constant amplitude residual swing in the 6 and 5 directions, while the nonlinear model shows transfer of
vibration from the 5 to the 6 direction. This transfer is evident in the experimental data of
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

12.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 11
Figure 11. Ratio of nonlinear to linear oscillation periods.
Figure 9. Figure 10 shows the nonlinear 6 vibration growing slightly as energy is transferred
from the 5 direction. The linear vibration stays the same, as expected, but the experimental vibration amplitude decreases with time. This is most likely due to damping in the real
system that is unaccounted for in either of the dynamic models. The experimental behavior
is close to the nonlinear predictions and, for the extreme motions examined in this example,
the nonlinear model shows a clear advantage over the linear model.
2.3. Nonlinear Transition
There are two assumptions that transform the nonlinear crane equations to the linearized
model
g
1
54 3 2 5 5 x9
4
L
L
g
1
64 3 2 6 5 y4 4
L
L
(9)
6 6]
6 9 1. As these terms
The first assumption is that the payload angular velocity is small: [59
appear as second-order terms in equation 1, they are neglected. The second assumption is
that the angular deflection is small: [59 6] 9 1. Using the small angle approximations for
sine and cosine yields the linearized model, which in turn yields a linear approximation of
the oscillation period. As these swing angles increase, the nonlinear period of oscillation
changes, as seen in Figure 11. These changes are small. For example, there is only a 5%
change in the oscillation period at a swing angle of 50
.
In most real crane operations, large swing angles and velocities are neither safe nor
useful. For most reasonable operating regimes (including the working range of the portable
bridge crane), the swing angles and velocities are small enough that there is virtually no
difference between the linear and nonlinear models. Owing to this, input shaping has been
shown to be very effective on bridge cranes (Starr, 19851 Singer et al., 19971 Hong and
Hong, 20041 Khalid et al., 20061 Sorensen et al., 20071 Singhose et al., 20081 Sorensen et al.,
2008). In fact, input shaping further suppresses the swing angles, thereby keeping the crane
operating in the linear regime and improving its own effectiveness.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

13.

12 D. BLACKBURN ET AL.
Figure 12. Tower crane schematic.
3. TOWER CRANE
3.1. System Model
An illustration of a tower crane is shown in Figure 12. The trolley slides along the boom in
the R direction, and the boom rotates around the mast in the s direction. If the suspension
cable length is constant, then the equations of motion relating the payload swing angles, 5
and 6, to the motion of the trolley in the R and s directions are (Blackburn et al., 2006):
2
L 54 5 L 66 cos 758 sin 758 5 g sin 758 cos 768
3 2 R4 cos 758 5 R s6 2 cos 758 2 R s4 sin 758 sin 768 2 2 R6 s6 sin 758 sin 768
2 2L s6 66 cos2 758 cos 768 2 L s4 sin 768 5 L s6 2 sin 758 cos2 768 cos 758
L 64 cos 758 2 2L 56 66 sin 758 5 g sin 768
3
R s4 cos 768 5 2 R6 s6 cos 768 5 2L s6 56 cos 758 cos 768
5 L s4 sin 758 cos 768 5 L s6 2 sin 768 cos 758 cos 768 4
(10)
With state space variables:
x 3
u 3
1
5 56 6
1
R4 s4
66
R
R6 s s6
2T
2T
we find the nonlinear state space equations:
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011
(11)

14.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 13
x61 3 x2
x62 3 2x 42 cos 7x1 8 sin 7x1 8 2 2x 8 x4 cos2 7x1 8 cos 7x3 8 2 u 2 sin 7x3 8
5 x82 sin 7x1 8 cos2 7x3 8 cos 7x1 8
5
1 9
2g sin 7x1 8 cos 7x3 8 2 u 1 cos 7x1 8 5 x5 x82 cos 7x1 8
x9
2
x5 u 2 sin 7x1 8 sin 7x3 8 2 2x6 x 8 sin 7x1 8 sin 7x 3 88
x63 3 x4
9
x64 3 2x2 x 4 tan 7x1 8 5 cos 7x 3 8 2x 8 x2 5 u 2 tan 7x1 8 5 x 82 sin 7x3 8
5
1
72g sin 7x3 8 5 x 5 u 2 cos 7x 3 8 5 2x6 x 8 cos 7x3 88
x9 cos 7x 1 8
x65 3 x6
x66 3 u 1
x67 3 x8
x68 3 u 2 4
(12)
Assuming a constant length, L 0 , and partially linearizing these states using equations 5 and
6, we obtain
3
6
0
1
0
0 0 0 0 0
4
7
4 g
7
42
7
0
0
0
0
0
0
0
4 L
7
4
0
7
4
7
4
7
4 0
0
0
1 0 0 0 07
4
7
4
7
g
4
7
4 0
0 2
0 0 0 0 07
7
L
Atwr 3 4
0
4
7
4
7
4 0
0
0
0 0 1 0 07
4
7
4
7
4
7
4 0
0
0
0 0 0 0 07
4
7
4
7
4 0
0
0
0 0 0 0 17
4
7
5
8
0
0
0
0 0 0 0 0
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

15.

14 D. BLACKBURN ET AL.
3
Btwr
0
4
4 1
42
4 L0
4
4
4 0
4
4
4
4 0
34
4
4
4 0
4
4
4
4 1
4
4
4 0
5
0
0
6
7
7
07
7
7
7
07
7
7
R7
7
L0 7
74
7
07
7
7
7
07
7
7
07
8
(13)
1
This linearization technique yields only quasi-linear matrices, with Btwr depending on R. It
was decided to linearize about a constant cable length and ignore hoisting in this linearization
while keeping some of the dependence of the dynamics on R. This method ignores dynamic
effects in R while allowing the instantaneous R to influence the swing angles. The resulting
quasi-linear system captures the cylindrical motion inherent in the system. For both the linear
and the nonlinear models, the payload position is given by
xpayload 3 [R 5 L sin 758] cos 7s8 5 [L sin 768 cos 758] sin 7s8
ypayload 3 [R 5 L sin 758] sin 7s8 2 [L sin 768 cos 758] cos 7s8 4
(14)
3.2. Model Verification
The tower crane used for experimental verification is shown in Figure 13. The crane is
approximately 2 m tall with a 1 m beam arm. The crane has three degrees of freedom
actuated by Siemens synchronous AC servo motors. The slewing motor controls the motion
about the vertical axis, which is capable of 340
rotation. The trolley moves radially via
a lead screw, and the hoisting motor controls the suspension cable length. In addition, a
Siemens digital camera is mounted onto the trolley and records the swing deflection of the
payload at a rate of 25 Hz. A Siemens PLC sends velocity setpoints to Siemens motor drives,
which use motor encoder signals to provide PI velocity feedback control (Lawrence et al.,
2006).
As the tower crane exhibits noticeable nonlinear behavior for nearly all moves, realistic
moves were performed and compared with the simulated responses. Figures 14 and 15 show
the responses for a combined slew and radial move. As can be seen, the nonlinear simulations
in Figure 14 predict crane behavior fairly well, while the linear model ignores all coupling
between radial and tangential motion. The deflection angles are also similar for the nonlinear
model and experimental data, as can be seen in Figures 16 and 17. Figure 16 shows that the
crane exhibits measurable damping in the radial direction. This is because the payload cable
runs through several pulleys in the radial direction. In order to achieve better agreement
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

16.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 15
Figure 13. Picture of portable tower crane.
Figure 14. Experimental and nonlinearly simulated payload trajectories.
with the experimental data, a small amount of viscous damping was added to the original
models.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

17.

16 D. BLACKBURN ET AL.
Figure 15. Experimental and linearly simulated payload trajectories.
Figure 16. Experimental and simulated radial swing angle (5 ).
Figure 17. Experimental and simulated tangential swing angle (6 ).
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

18.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 17
Figure 18. Unshaped slew of tower crane.
Figure 19. Swing angles during unshaped slew.
3.3. Input Shapers for Tower Crane Slewing
In order to improve the performance of input shaping on tower cranes, we endeavor to design
an input shaper to deal with the specific nonlinearities associated with slewing motions of
tower cranes. As the boom rotates, the payload tends to swing outward in the radial direction
owing to a lack of centripetal force provided by the suspension cables. When the move is
completed, the payload will then oscillate in the radial direction. Also, from equation 10, we
see that there are inherent interactions that cause the rotational and radial velocities to affect
both swing angles.
To investigate these effects, we simulated a move with a trapezoidal slewing velocity
profile that drives the crane through a circular rest-to-rest motion. Figure 18 shows an overhead view of the move, and Figure 19 shows the radial and tangential swing angles during
the move.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

19.

18 D. BLACKBURN ET AL.
Figure 20. Vector representation of traditional ZV shaping.
The swing angles show two dominant frequencies: the 0.5 Hz natural frequency corresponding to classical pendulum motion and another arising from the angular velocity, , of
the boom rotation. The low-frequency envelope that bounds the radial vibration amplitude is
very nearly 90
out of phase with the envelope that bounds the tangential swing angle. We
conclude that this is due to the transfer of momentum from the radial to tangential direction
as the payload moves through 90
of rotation. That is, once the boom has rotated 90
, the
original orientations of the radial and tangential directions have now exactly switched: the
radial direction is now in the original tangential direction, and vice versa. This indicates that
a conservation of linear momentum effect is more dominant than nonlinear interactions in
the equations of motion.
A traditional ZV shaper convolved with a slewing profile will yield two accelerations
in the tangential direction, as represented by the vectors in Figure 20. However, owing to
the rotational nature of the tower crane, these accelerations are not in the same direction1
the second acceleration has been rotated through an angle of

20.

s. This effect degrades the
performance of traditional input shapers because they rely on the second acceleration to
cancel the vibration induced by the first acceleration.
The importance of momentum effects leads us to consider the multi-axis input shaper
illustrated in Figure 21. This input shaper is designed for a pure rotational move. In order
to better cancel the vibration induced by the first impulse, we would like the second impulse
to act in the same direction as the first impulse. This leads us to add radial components to
the slewing motion to achieve the same resultant direction for both accelerations, as seen in
Figure 21. By setting
A2 3 cos 7

21.

s8
B2 3 sin 7

22.

s8
(15)
we obtain a resultant vector, V2 , that acts in the same direction as the first impulse, allowing
more of the vibration to be cancelled. This vector alignment approach is the general design
method for the improved slewing shaper developed in this paper.
In order to justify this vector approach, it is necessary to determine whether or not induced vibration is influenced by slewing motion of the crane. To do this, two moves were
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

23.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 19
Figure 21. Vector representation of slewing input shaper.
Figure 22. Effect of slew on initial vibration.
performed and compared. The crane was moved through a slew both with and without initial swing of the payload. The zero initial conditions response was then subtracted from the
full response to determine the effect of the move on the initial vibration. As can be seen in
Figure 22, the orientation of the original vibration remains nearly unchanged.
There are several challenges to implementing this advanced shaper. The most significant
is the fact that adding a single impulse in the radial direction causes a nonzero radial velocity
following the second acceleration. By ignoring this effect, we are able to suppress the swing
angles, but it leads to significant radial drift for large angular rotations, as seen in Figure 23.
Therefore, this approach can be improved by applying a radially inward impulse during
the first acceleration, followed by an equal magnitude outward impulse during the second
acceleration. This approach is illustrated in Figure 24. The resulting motion will have no
radial velocity during the constant-velocity portion of the slew.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

24.

20 D. BLACKBURN ET AL.
Figure 23. Slew of tower crane with nonlinear slewing shaper.
Figure 24. Improved slewing shaper.
The shaper consists of two sets of impulses, one for angular motions, and one for radial
motions. This is represented as:
Ai
ti
Bi
ti
3
3
1
0
2 1
0
2
T 32
1
T 32
(16)
where Ai are the impulse amplitudes in the slewing direction, Bi are those
in the radial
direction, and ti are the impulse times. Setting V1 3 V2 and constraining
Ai 3 1 yields:
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

25.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 21
Figure 25. Simulated unshaped and shaped residual vibration (s4 3 120
s22 , tr 3 045 s).
1 5 2 3 19 1 3 1 R0
1 s4 tr
2 R0 2
7T 2 tr 8 3 1 R0
2
(17)
where R0 is the starting radial position of the trolley, s4 is the acceleration of a baseline
trapezoidal velocity profile with rise time, tr T 32, and
3
1
[1 5 cos 7

26.

s8] cot 7

27.

s8 5 sin 7

28.

s8
3

29.

s 3
1 5 cos 7

30.

s8
sin 7

31.

s8
1 s4 tr
7T 2 tr 8 4
2
(18)
Equations 17 and 18 can be solved for the three unknowns, 1 , 2 and 1 , using a standard
nonlinear solver. This process is an easy numerical operation and only depends on three
crane parameters, s4 , tr and R0 . Once the shapers are determined, they are both convolved
with the angular velocity profile to obtain shaped velocity profiles for the radial and slewing
directions. To avoid actuator saturation, it is important to check that 1 s4 does not exceed the
4
maximum acceleration in the radial direction, R.
To measure the effectiveness of this new command-shaping process, we compare the
final residual vibration for unshaped, ZV shaped and ZVD shaped moves against a move
created using the slewing shaper defined by equation 16. Figure 25 shows the performance
of the three shapers compared with the unshaped case for R0 3 0455 m, and L 0 3 1 m. It is
clearly evident that any form of input shaping is a vast improvement over the unshaped case
for nearly all move distances, even for very aggressive moves.
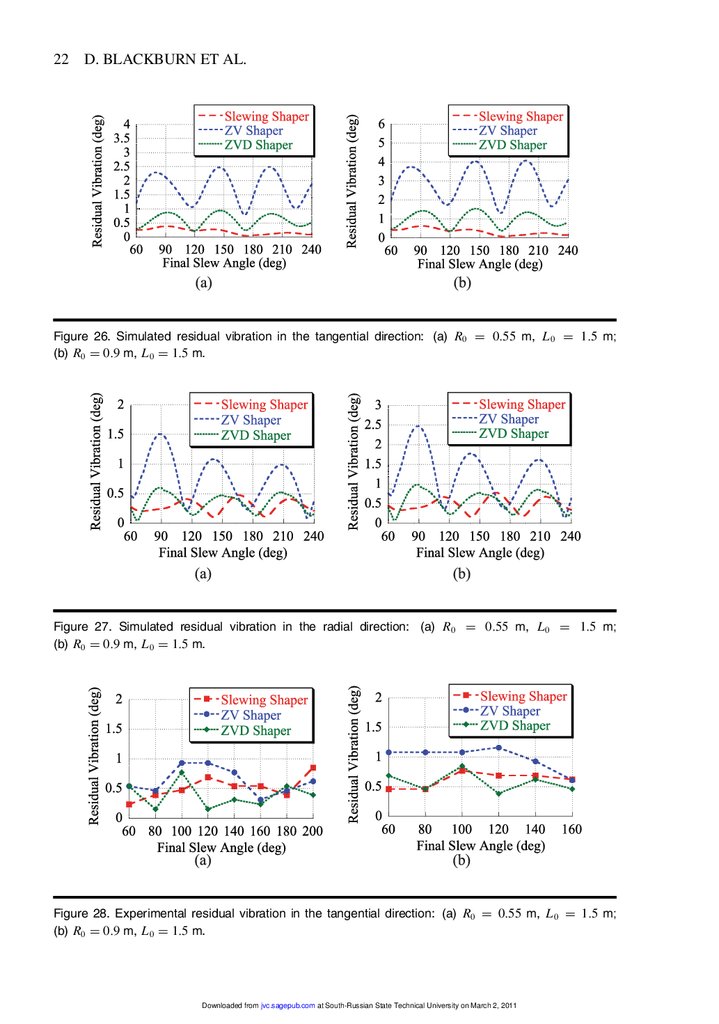
Figures 26 and 27 show simulated residual vibration in the tangential and radial directions for various rotation angles and system parameters. Figures 28 and 29 show the
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

32.

22 D. BLACKBURN ET AL.
Figure 26. Simulated residual vibration in the tangential direction: (a) R0 3 0455 m, L 0 3 145 m1
(b) R0 3 049 m, L 0 3 145 m.
Figure 27. Simulated residual vibration in the radial direction: (a) R0 3 0455 m, L 0 3 145 m1
(b) R0 3 049 m, L 0 3 145 m.
Figure 28. Experimental residual vibration in the tangential direction: (a) R0 3 0455 m, L 0 3 145 m1
(b) R0 3 049 m, L 0 3 145 m.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

33.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 23
Figure 29. Experimental residual vibration in the radial direction: (a) R0 3 0455 m, L 0 3 145 m1
(b) R0 3 049 m, L 0 3 145 m.
corresponding experimental results. The experimental results show similar trends to the simulations, but the slewing shaper does not perform as well as the theory predicts in the radial
direction. The increase in vibration is most likely due to the hardware being unable to track
the radial command precisely. The radial velocity profiles have very small magnitudes, magnifying the error signal with respect to the desired velocity. Typical velocity errors seen in
the experiments were 14%. To improve performance, the feedback gains used in the radial direction could have been optimized for slow velocities, but this modification was not
performed.
4. CONCLUSIONS
Nonlinear equations of motion were presented for bridge and tower crane payload motion and
verified experimentally. A novel command-shaping algorithm based on nonlinear directional
effects improved the performance of ZV shaping in tower crane slewing motions. This multiaxis shaper requires only minimal knowledge of the system parameters. It does not delay the
system any more than traditional ZV shaping and also provides a significant performance
increase. Experimental results verify that this command-shaping method is more effective
than traditional input shaping for reducing vibration in the direction of slewing motions. This
development advances the current state of input-shaping technology on nonlinear systems by
improving vibration reduction and offering a new perspective on the problem of rotational
motion. The vector-based algorithm represents a new approach to command shaper design
for tower cranes and could also be extended to boom cranes, as well as more robust input
shapers such as ZVD and EI.
Acknowledgements. The authors would like to thank Siemens Energy and Automation and the 21st Century Center of
Excellence in Robotics at the Tokyo Institute of Technology for their support of this work.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

34.

24 D. BLACKBURN ET AL.
REFERENCES
Abdel-Rahman, E. M., Nayfeh, A. H., and Masoud, Z. N., 2003, “Dynamics and control of cranes: A review,”
Journal of Vibration and Control 9(7), 863–908.
Banerjee, A. K., Pedreiro, N., and Singhose, W. E., 2001, “Vibration reduction for flexible spacecraft following
momentum dumping with/without slewing,” AIAA Journal of Guidance, Control, and Dynamics 24(3), 417–
427.
Blackburn, D., Singhose, W., Kitchen, J., Patrangenaru, V., Lawrence, J., Kamoi, T., and Taura, A., 2006, “Advanced input shaping algorithm for nonlinear tower crane dynamics,” in Proceedings 8th International Conference on Motion and Vibration Control, Daejeon, Korea, August 27–30, KAIST.
Hong, K.-T. and Hong, K.-S., 2004, “Input shaping and VSC of container cranes,” in IEEE International Conference
on Control Applications, Taipei, Taiwan, September 2–4, pp. 1570–1575.
Hu, Q. and Ma, G., 2005, “Vibration suppression of flexible spacecraft during attitude maneuvers,” AIAA Journal
of Guidance, Control, and Dynamics 28(2), 377–380.
Hyde, J. M. and Seering, W. P., 1991, “Using input command pre-shaping to suppress multiple mode vibration,”
in IEEE International Conference on Robotics and Automation, Sacramento, CA, April 9–11, Vol. 3, IEEE,
pp. 2604–2609.
Khalid, A., Huey, J., Singhose, W., Lawrence, J., and Frakes, D., 2006, “Human operator performance testing using
an input-shaped bridge crane,” Journal of Dynamic Systems, Measurement, and Control 128, 835–841.
Lawrence, J., Fatkin, B., Singhose, W., Weiss, R., Erb, A., and Glauser, U., 2006, “An Internet-driven tower crane
for dynamics and controls education,” in 7th IFAC Symposium on Advances in Control Education, Madrid,
Spain, June 21–23.
Lawrence, J. and Singhose, W., 2005, “Design of a minicrane for education and research,” in 6th International
Workshop on Research and Education in Mechatronics, Annecy, France, June 30–July 1, pp. 254–
259.
Masoud, Z. N., Nayfeh, A. H., and Al-Mousa, A., 2003, “Delayed position feedback controller for the reduction of
payload pendulations of rotary cranes,” Journal of Vibration and Control 9(1–2), 257–277.
Singer, N., Singhose, W., and Kriikku, E., 1997, “An input shaping controller enabling cranes to move without
sway,” in ANS 7th Topical Meeting on Robotics and Remote Systems, Augusta, GA, April 27–May 1, Vol. 1,
pp. 225–231.
Singer, N. C. and Seering, W. P., 1990, “Preshaping command inputs to reduce system vibration,” ASME Journal of
Dynamic Systems, Measurement, and Control 112, 76–82.
Singer, N. C. and Seering, W. P., “An extension of command shaping methods for controlling residual vibration
using frequency sampling,” in IEEE International Conference on Robotics and Automation, Nice, France,
May 12–14, Vol. 1, pp. 800–805.
Singhose, W., Banerjee, A. K., and Seering, W. E., 1997a, “Slewing flexible spacecraft with deflection limiting
input shaping,” AIAA Journal of Guidance, Control, and Dynamics 20(2), 291–298.
Singhose, W., Crain, E., and Seering, W., 1997b, “Convolved and simultaneous two-mode input shapers,” IEE
Proceedings—Control Theory Applications 144(6), 515–520.
Singhose, W., Kim, D., and Kenison, M., 2008, “Input shaping control of double-pendulum bridge crane oscillations,” ASME Journal of Dynamic Systems, Measurement, and Control 130, 034504.
Singhose, W., Seering, W., and Singer, N., 1994, “Residual vibration reduction using vector diagrams to generate
shaped inputs,” ASME Journal of Mechanical Design 116(2), 654–659.
Singhose, W. E., Seering, W. P., and Singer, N. C., 1996, “Input shaping for vibration reduction with specified
insensitivity to modeling errors,” in Japan-USA Symposium on Flexible Automation, Boston, MA, July 7–
10.
Smith, O. J. M., 1958, Feedback Control Systems, McGraw-Hill, New York, pp. 331–345.
Smith, R., Starr, G. P., Lumia, R., and Wood, J., 2004, “Preshaped trajectories for residual vibration suppression in
payloads suspended from multiple robot manipulators,” in IEEE International Conference on Robotics and
Automation, New Orleans, LA, April 26–May 1, pp. 1599–1603.
Sorensen, K., Singhose, W., and Dickerson, S., 2007, “A controller enabling precise positioning and sway reduction
in bridge and gantry cranes,” Control Engineering Practice 15(7), 825–837.
Sorensen, K. L., Danielson, J., and Singhose, W. E., 2008, “Anti-sway and positioning control for an industrial
bridge crane with multi-mode dynamics,” in ASME International Symposium on Flexible Automation, Atlanta, GA, June 23–26.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011

35.

COMMAND SHAPING FOR NONLINEAR CRANE DYNAMICS 25
Starr, G. P., 1985, “Swing-free transport of suspended objects with a path-controlled robot manipulator,” Journal of
Dynamic Systems, Measurement, and Control 107, 97–100.
Tallman, G. H. and Smith, O. J. M., 1958, “Analog study of dead-beat posicast control,” IRE Transactions on
Automatic Control 4(1), 14–21.
Watanabe, T., Makida, T., Fujii, H. A., Kojima, H., and Singhose, W., 2004, “An application of input shaping for
electroynamic tether system,” in AIAA/AAS Astrodynamics Specialists Conference, Providence, RI, February
8–12.
Downloaded from jvc.sagepub.com at South-Russian State Technical University on March 2, 2011