Дифракция света

1.

Лекция 9
ДИФРАКЦИЯ
СВЕТА
Вопросы:
1. Принцип Гюйгенса-Френеля.
Метод зон Френеля.
2. Виды дифракции света. Дифракция
на простейших преградах.
3. Дифракционная решетка.

2.

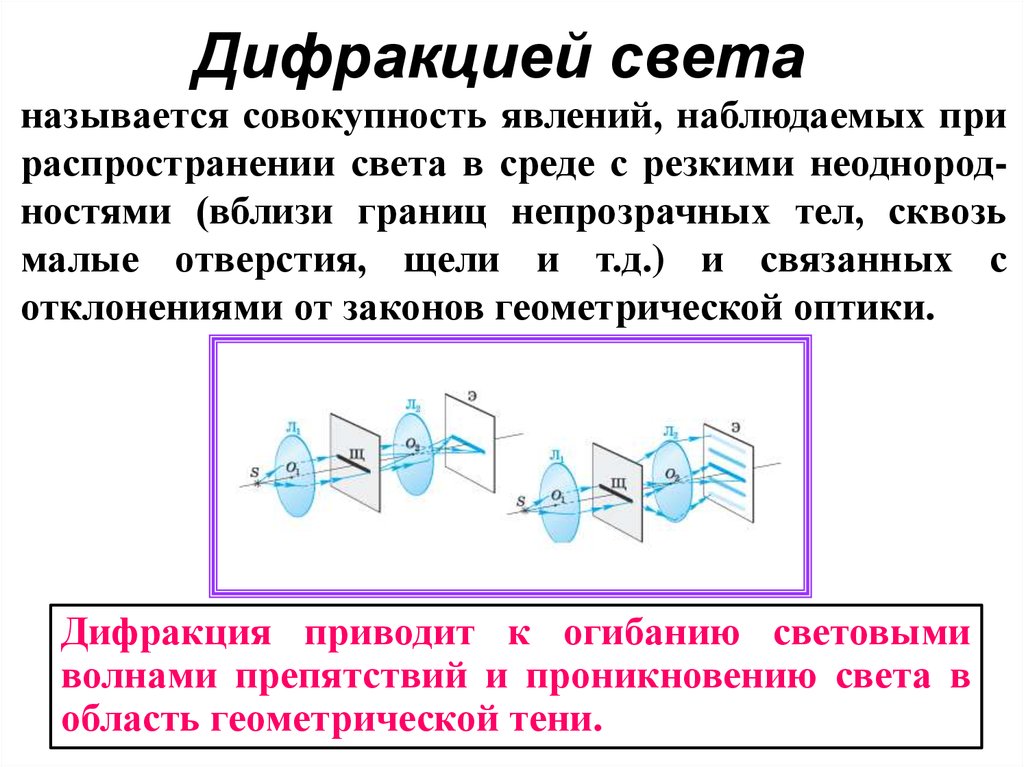
Дифракцией света
называется совокупность явлений, наблюдаемых при
распространении света в среде с резкими неоднородностями (вблизи границ непрозрачных тел, сквозь
малые отверстия, щели и т.д.) и связанных с
отклонениями от законов геометрической оптики.
Дифракция приводит к огибанию световыми
волнами препятствий и проникновению света в
область геометрической тени.

3.

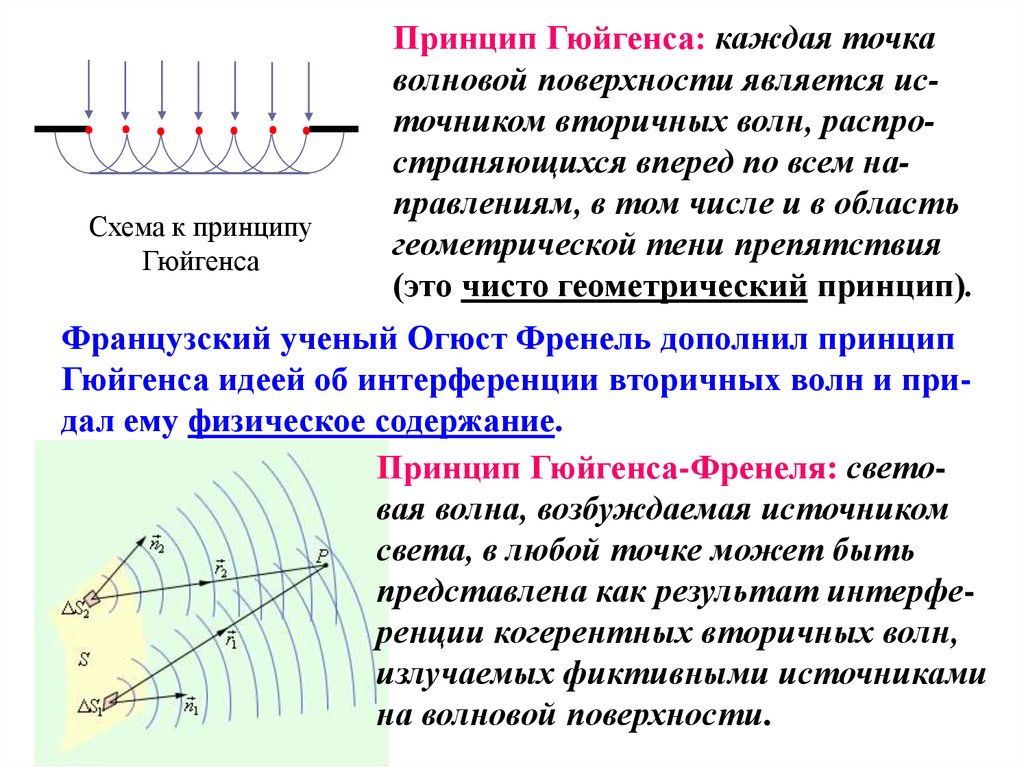
Схема к принципу
Гюйгенса
Принцип Гюйгенса: каждая точка
волновой поверхности является источником вторичных волн, распространяющихся вперед по всем направлениям, в том числе и в область
геометрической тени препятствия
(это чисто геометрический принцип).
Французский ученый Огюст Френель дополнил принцип
Гюйгенса идеей об интерференции вторичных волн и придал ему физическое содержание.
Принцип Гюйгенса-Френеля: световая волна, возбуждаемая источником
света, в любой точке может быть
представлена как результат интерференции когерентных вторичных волн,
излучаемых фиктивными источниками
на волновой поверхности.

4.

P3
п
m
P2
Метод зон Френеля
b
b+ /2
b+2 /2
Волновая поверхность разбивается на кольцевые зоны, являющиеся источниками когерентных вторичных световых
волн, которые действуют в
противофазе друг с другом.
P1
S0
P0
P
b+4 /2
b+3 /2
Ф
Схема формирования
зон Френеля
Р1Р Р0Р = Р2Р P1P =… = /2
А = А1 А2 + А3 А4 + …
– амплитуда результирующего
светового колебания в точке Р.
Таким образом, действие сферической световой волны от
точечного источника S0 заменяется действием фиктивных
источников когерентных вторичных волн.

5.

п
m
C
r a a hm
2
m
a
rm
2
2
b m
2
a; b
hm
S0
P0
D
P
b
Ф
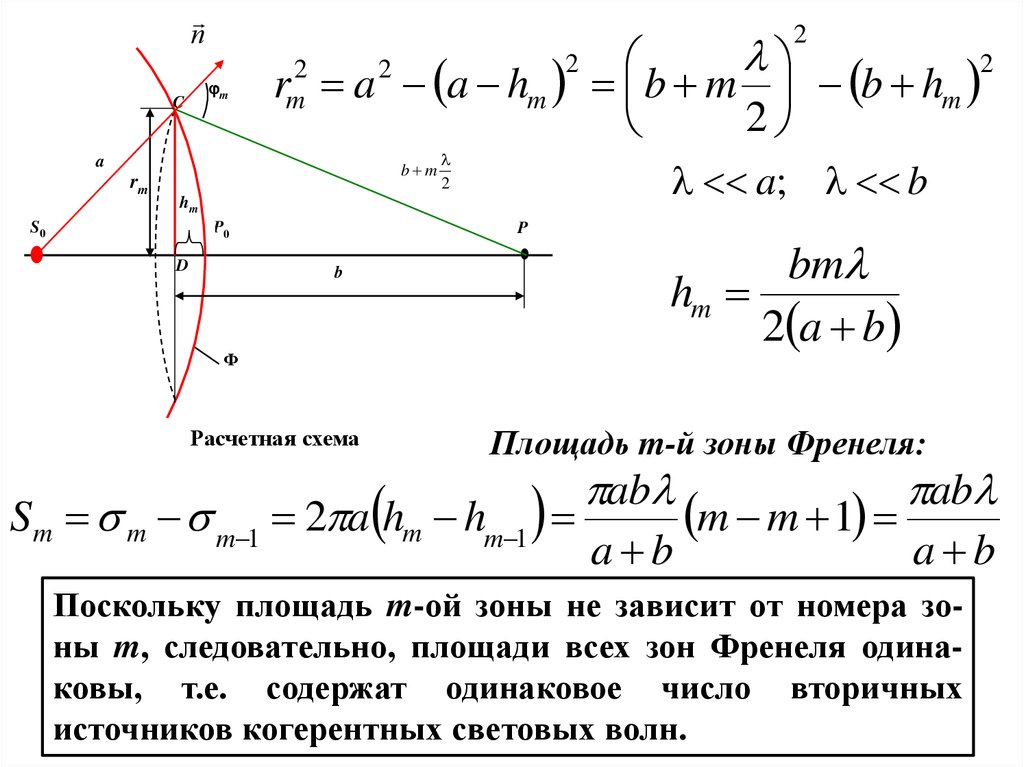
Расчетная схема
2
b m b hm
2
2
bm
hm
2 a b
Площадь m-й зоны Френеля:
Sm m m 1 2 a hm hm 1
ab
a b
m m 1
ab
a b
Поскольку площадь m-ой зоны не зависит от номера зоны m, следовательно, площади всех зон Френеля одинаковы, т.е. содержат одинаковое число вторичных
источников когерентных световых волн.

6.

Оценка общего числа зон Френеля и радиуса m-ой зоны:
a b 10 см 0,1 м; 0,5 мкм;
2
2
2 a
2 a
2a a b
a b
N
8 105
Sm
ab
b
A A
,
Поскольку А А А ... A ... и A
2
A A
A
A
то: A A A A ...
2 2
2
.
A
A
A
A ...
2
2
2
m 1
1
2
3
m
m
1
1
2
1
3
3
m 1
3
2
5
1
4
Вывод: колебания, вызываемые в точке Р полностью открытой сферической волновой поверхностью, имеют такую же
амплитуду, как если бы действовала только половина центральной зоны Френеля.

7.

ab
r
m 0,158 мм (m 1)
a b
m
Следовательно, свет от источника S0 в точку Р распространяется в пределах очень узкого прямого канала, т.е. прямолинейно.
Справедливость метода зон Френеля
подтверждается действием зонных
пластинок – круглых пластинок, состоящих из чередующихся прозрачных и непрозрачных колец, оставляющих открытыми только несколько нечетных (или четных) зон.
Зонные пластинки резко усиливают интенсивность проходящего света, напр., если открыты 1-я, 3-я и 5-я зоны, то I≈36I0.

8.

Критерий дифракции света
Характерные размеры задачи:
d – характерный линейный размер препятствия;
b – расстояние до точки наблюдения;
λ – длина волны света.
2
d
b
– критерий дифракции (по порядку величины
равен числу зон Френеля, укладывающихся
на препятствии, для точки, лежащей против
середины препятствия).

9.

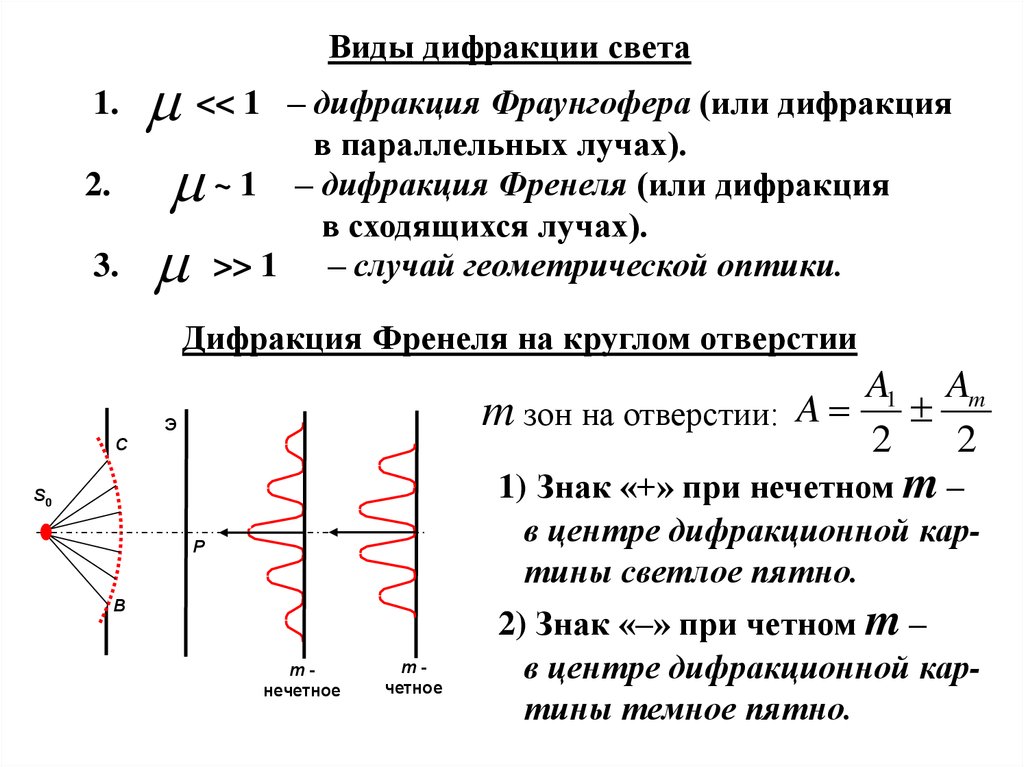
Виды дифракции света
1.
2.
3.
<< 1 – дифракция Фраунгофера (или дифракция
в параллельных лучах).
~ 1 – дифракция Френеля (или дифракция
в сходящихся лучах).
>> 1 – случай геометрической оптики.
Дифракция Френеля на круглом отверстии
A1 Am
m зон на отверстии: A
2
2
Э
C
1) Знак «+» при нечетном m –
в центре дифракционной картины светлое пятно.
S0
P
B
mнечетное
mчетное
2) Знак «–» при четном m –
в центре дифракционной картины темное пятно.

10.

Дифракция Френеля на диске
C
Диск закрывает m зон Френеля:
Э
A
A
A
A
A
...
2 2
2
m 1
S0
m 1
m 3
m 2
P
B
Am 1
A
2
В центре картины (точка Р ) при
любом (как четном, так и нечетном)
m наблюдается светлое пятно.
Опыт по дифракции на диске, продемонстрированный на заседании
Парижской Академии наук в 1818 г. и
доказавший наличие светлого пятна
в центре тени, отбрасываемой
диском, принес всеобщее признание
волновой теории света.

11.

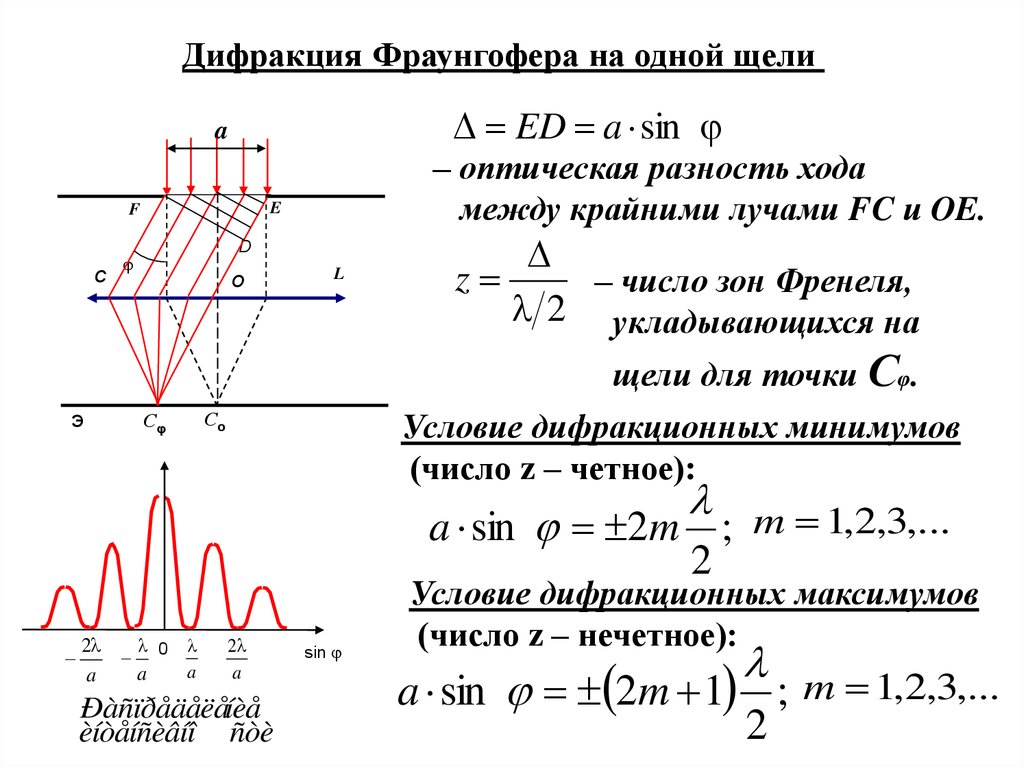
Дифракция Фраунгофера на одной щели
ED a sin
a
E
F
С
– оптическая разность хода
между крайними лучами FC и OE.
D
О
L
z
– число зон Френеля,
2 укладывающихся на
щели для точки Сφ.
Э
С
Условие дифракционных минимумов
(число z – четное):
Со
m 1,2,3,...
a sin 2m ;
2
λ
2λ
2λ λ 0 λ
a
a
a
a
a
2λ
a
Ðàñïðåäåëåíèå
èíòåíñèâíî ñòè
sin
Условие дифракционных максимумов
(число z – нечетное):
m 1,2,3,...
a sin 2m 1 ;
2

12.

Дифракционная решетка
Дифракционная решетка – это
периодическая структура, состоящая из параллельных щелей
равной ширины, лежащих в одной плоскости и разделенных
равными по ширине непрозрачными промежутками.
x
E
C
F
D
a b
d
L2
Э
C
Co
Схема дифракции
Фраунгофера на решетке
d a b
– период решетки.
У современных решеток приходится
до (1/d) = 2000 штрихов на миллиметр.
В решетке осуществляется
многолучевая интерференция
когерентных дифрагированных
пучков света от всех щелей.

13.

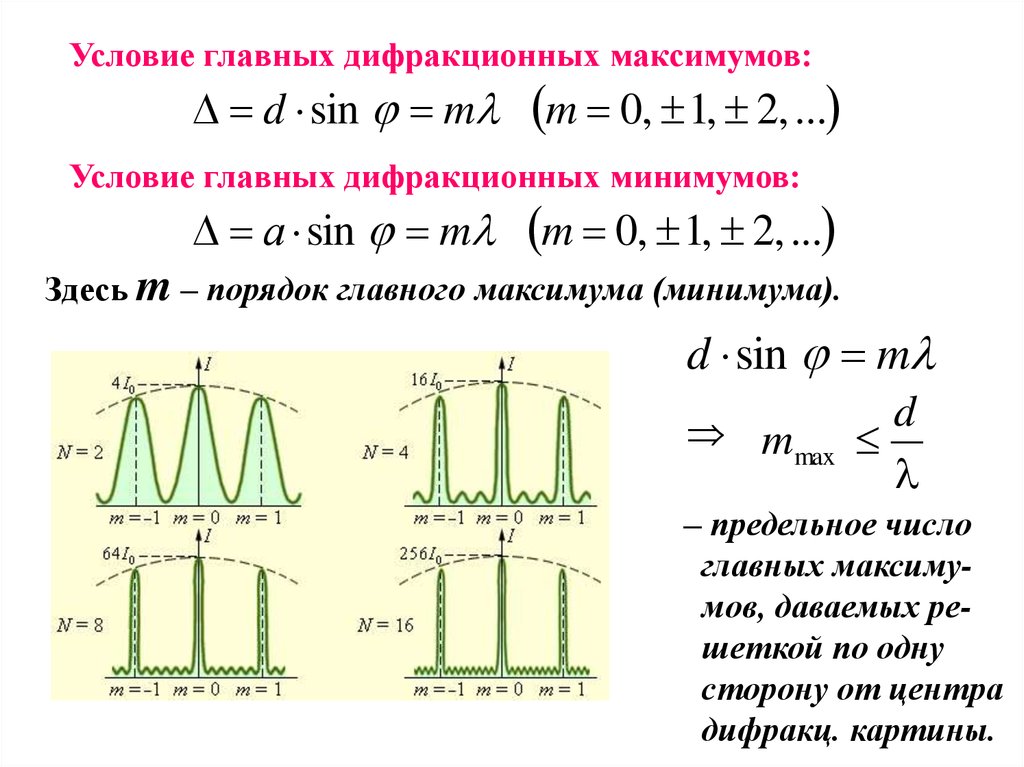
Условие главных дифракционных максимумов:
d sin m
m 0, 1, 2, ...
Условие главных дифракционных минимумов:
а sin m
m 0, 1, 2, ...
Здесь m – порядок главного максимума (минимума).
d sin m
m
max
d
– предельное число
главных максимумов, даваемых решеткой по одну
сторону от центра
дифракц. картины.

14.

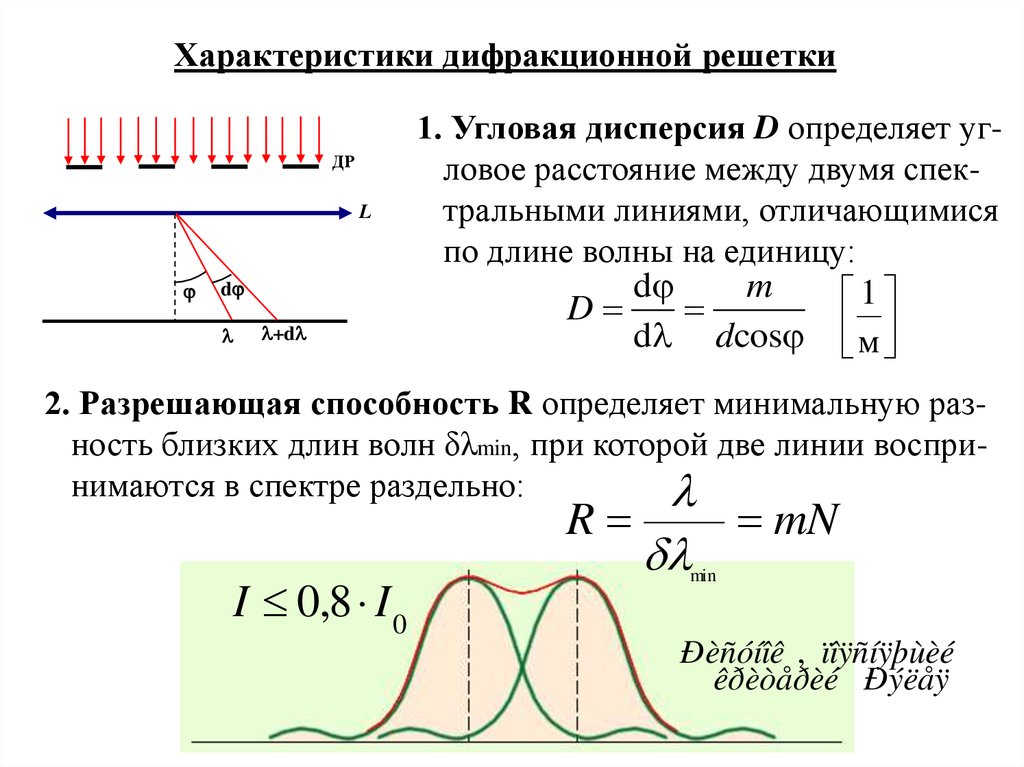
Характеристики дифракционной решетки
ДР
L
d
+d
1. Угловая дисперсия D определяет угловое расстояние между двумя спектральными линиями, отличающимися
по длине волны на единицу:
d
m
1
D
d dcos м
2. Разрешающая способность R определяет минимальную разность близких длин волн δλmin, при которой две линии воспринимаются в спектре раздельно:
R
I 0,8 I 0
mN
min
Ðèñóíîê , ïîÿñíÿþùèé
êðèòåðèé Ðýëåÿ