Похожие презентации:
Дифракция света
1.
ДИФРАКЦИЯ СВЕТА1
2.
Дифракцией света называетсясовокупность явлений наблюдаемых при
распространении света в средах,
включающих в себя неоднородности, из-за
наличия которых наблюдается отклонение
в распространении от законов
геометрической оптики. Частным случаем
проявления дифракции света является
огибание световыми волнами препятствий
и проникновение света в область
геометрической тени.
2
3.
34.
Наблюдение дифракции осуществляетсяпо следующей схеме: На пути световой
волны, распространяющейся от
некоторого источника, помещается
непрозрачная преграда, закрывающая
часть волновой поверхности световой
волны. За преградой располагается экран,
на котором возникает дифракционная
картина.
4
5.
Различают два вида дифракции. Еслиисточник света S и точка наблюдения P
расположены от препятствия настолько
далеко, что лучи падающие на
препятствие, и лучи идущие в точку P
образуют практически параллельные
пучки, говорят о дифракции в
параллельных лучах или о дифракции
Фраунгофера. В противном случае говорят
о дифракции Френеля.
5
6.
Критерий вида дифракции:1
2
r
1
b
1
- дифракция Фраунгофера
- дифракция Френеля
- геометрическая оптика
r – линейный размер препятствия,
b – расстояние от препятствия до экрана
6
7.
Впервые объяснения по распространениюсвета и дифракционным явлениям
попытался дать Гюйгенс и Френель.
Френель Огюст Жан
Фраунгофер Йозеф
(1788 - 1827)
французский физик, член
Парижской академии наук.
(1787- 1826)
немецкий физик, профессор
Мюнхенского университета.7
8.
Принцип Гюйгенса - ФренеляКаждая точка фронта
волны является источником
вторичных волн, огибающая
которых образует новый
фронт волны.
Принцип Гюйгенса развил
далее Френель, введя поло -
жение о когерентности и интерференции
этих вторичных волн.
8
9.
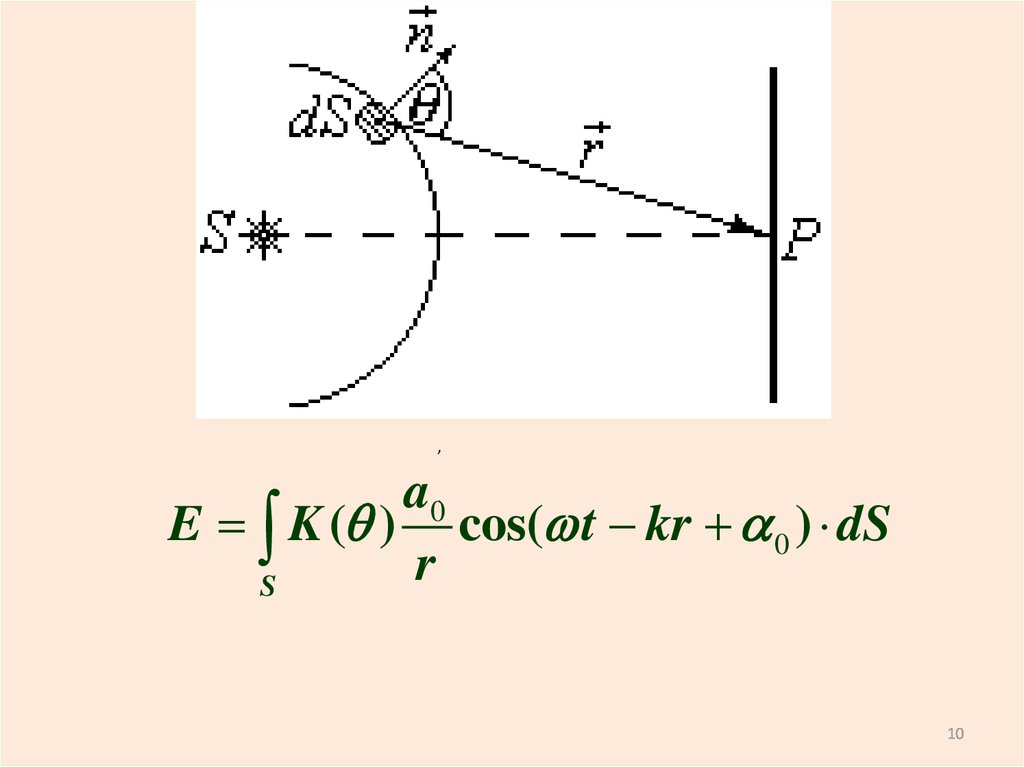
от каждого участка dS волновой поверхности в точкунаблюдения P, лежащую перед этой
поверхностью приходит колебание
a0dS
dE K
cos( t kr 0 )
r
,
.
а0 - определя-
ется амплитудой светового колебания в том
месте, где находится dS. При q = 0 K —
максимален, при q
2
— K = 0.
9
10.
,a0
E K (q ) cos( t kr 0 ) dS
r
S
.
10
11.
Зоны Френелякак показал Френель, волновую
поверхность надо разбивать не
произвольно, а по зонам, что упрощает
расчет амплитуды результирующего
колебания. Поверхность разбивается на
кольцевые зоны Френеля.
11
12.
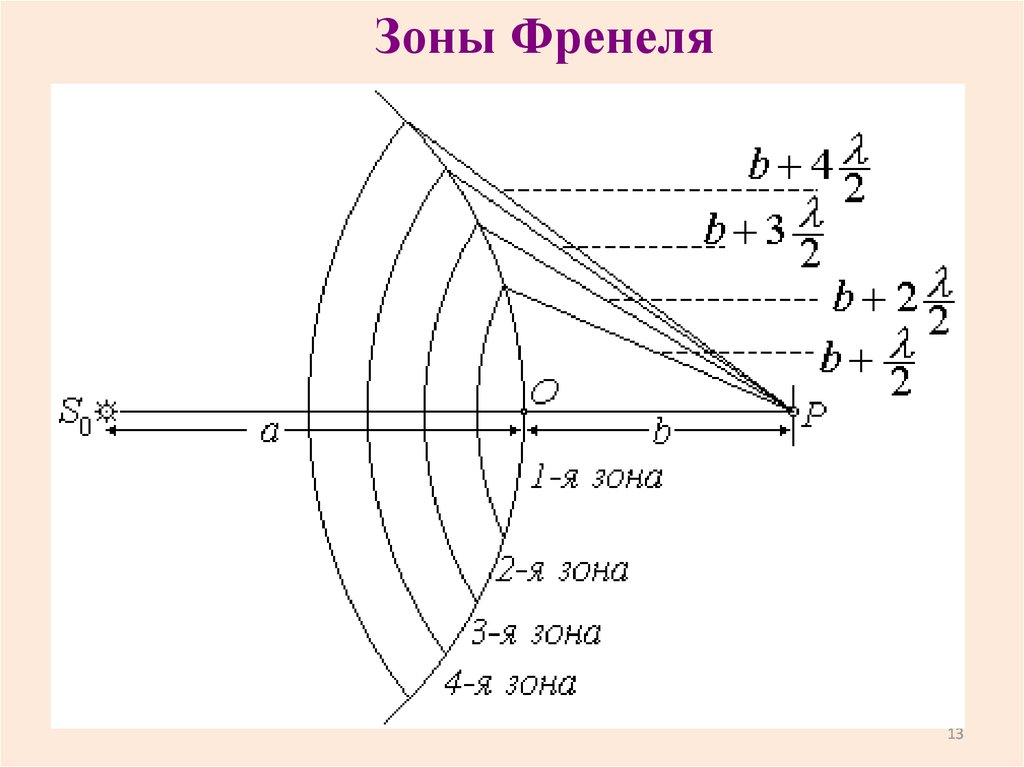
Зоны ФренеляДля построения зон проводятся сферы
радиусами , b m
(m = 1, 2, 3 …). В этом
2
случае, колебания, возбуждаемые в точке
P двумя соседними зонами,
противоположны по фазе, так как
разность хода от сходственных точек этих
зон до точки P равна
и эти колебания
2
будут гасить друг друга.
12
13.
Зоны Френеля13
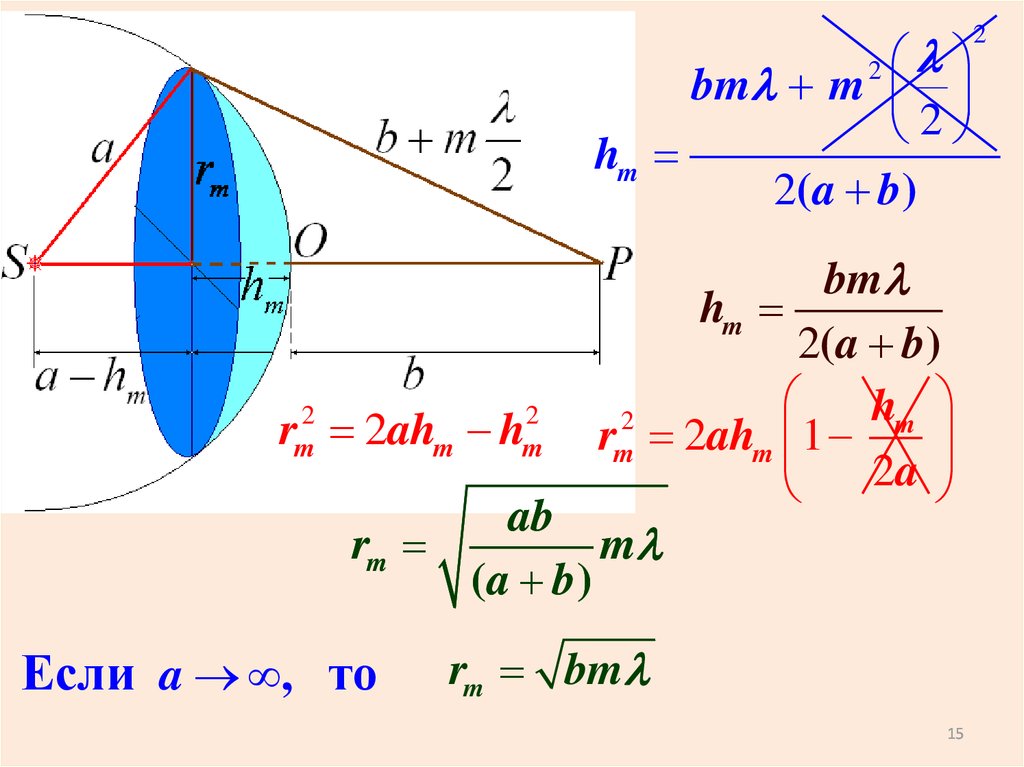
14.
Найдем радиусы иплощади зон
Френеля
rm2 a 2 (a hm )2
rm2 2ahm hm2
2
r b m b hm
2 2
2
2
rm bm m 2bhm hm2
2
2
m
2
2ahm h bm m 2bhm hm2
2
2
m
2
2
14
15.
bm m2
hm
2(a b )
2
bm
hm
2(a b )
hm
2
2
2
rm 2ahm hm rm 2ahm 1
2a
ab
rm
m
(a b)
Если a , то
rm bm
15
2
16.
bmhm
2(a b )
Площадь
сегмента
S 2 Rh
abm
Sm
a b
Площадь m-ой зоны DSm
DSm Sm Sm 1
DSm
ab
a b
Площади зон одинаковы
16
17.
S1- ая зона
2- ая зона
3- ая зона
4- ая зона
Для нахождения амплитуды результирующего
P колебания в
точке P
воспользуемся методом
векторных
диаграмм.
Для этого каждую зону Френеля разобьём еще на
более мелкие кольцевые участки, в пределах
каждого из которых фазу колебаний считают
постоянной, а при переходе от одного участка к
другому считают, что фаза изменяется
скачком.
17
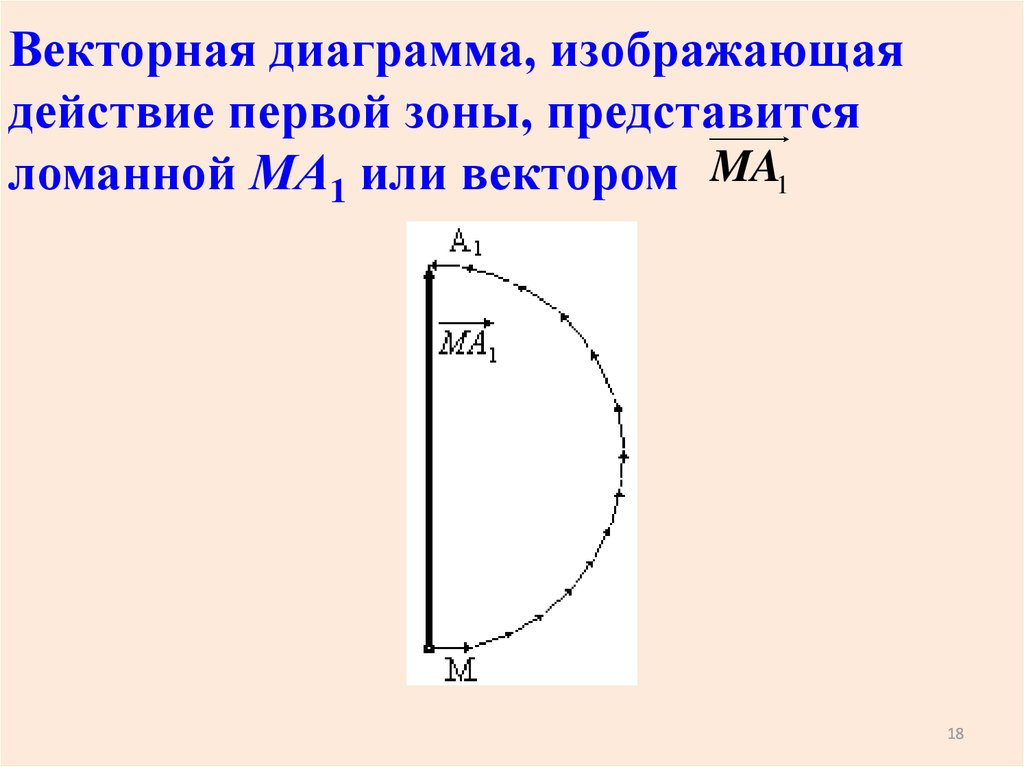
18.
Векторная диаграмма, изображающаядействие первой зоны, представится
ломанной МА1 или вектором MA1
18
19.
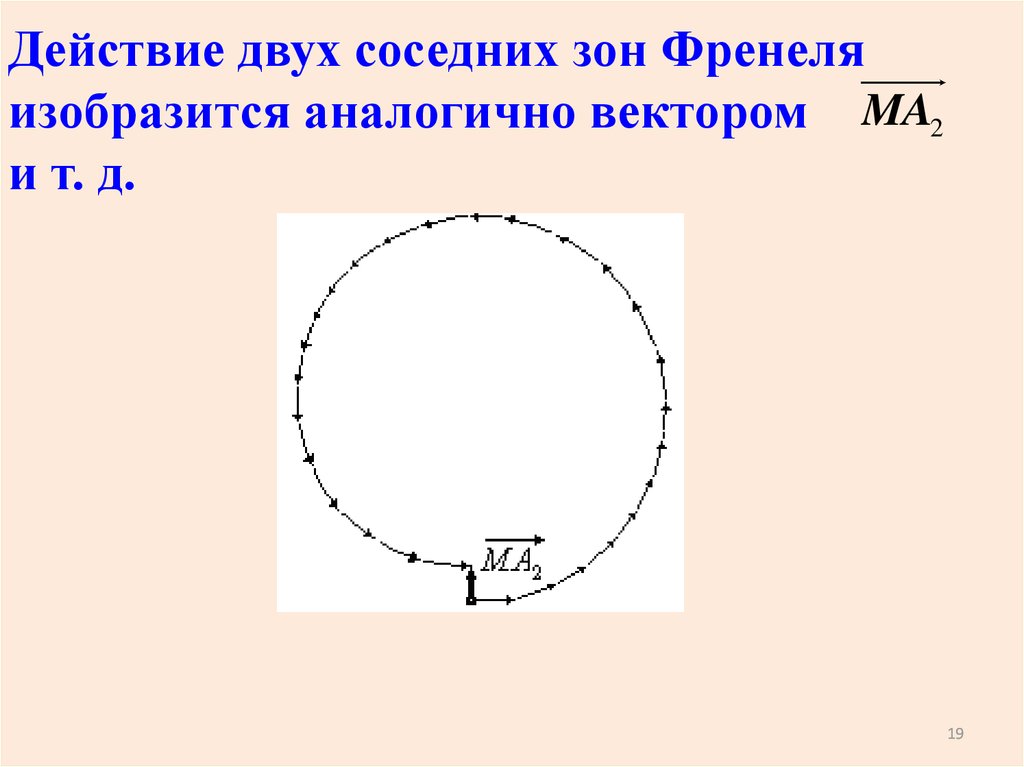
Действие двух соседних зон Френеляизобразится аналогично вектором MA2
и т. д.
19
20.
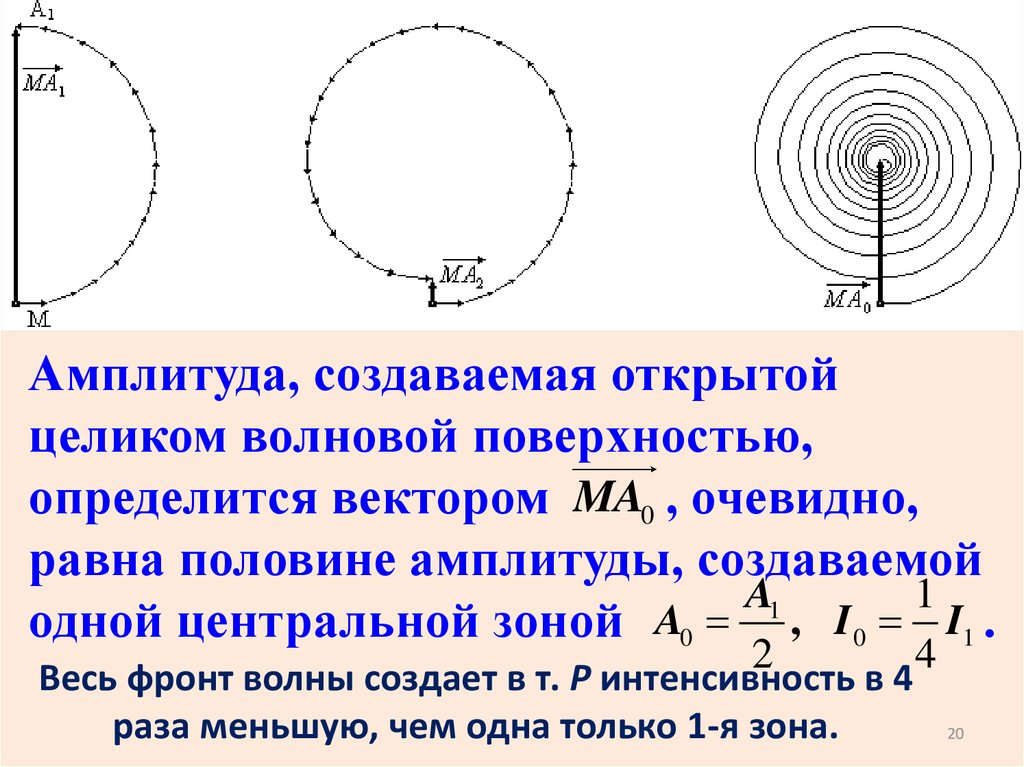
Амплитуда, создаваемая открытойцеликом волновой поверхностью,
определится вектором MA0 , очевидно,
равна половине амплитуды, создаваемой
A1
1
одной центральной зоной A0 , I 0 I1 .
2
Весь фронт волны создает в т. Р интенсивность в 4
раза меньшую, чем одна только 1-я зона.
4
20
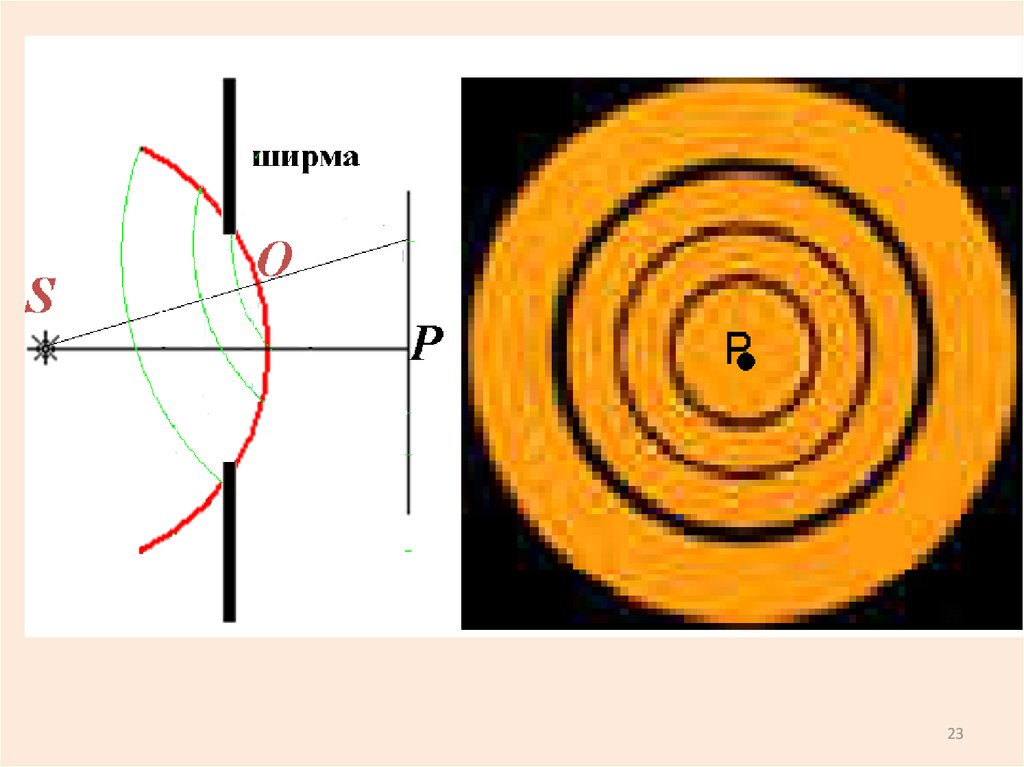
21.
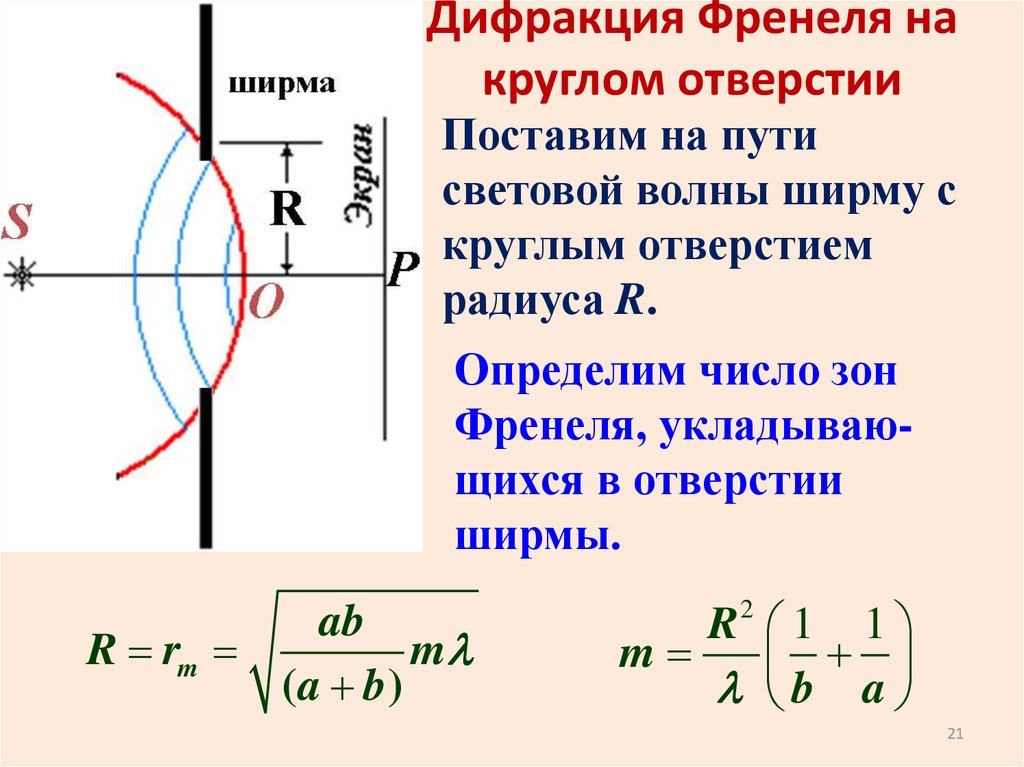
Дифракция Френеля накруглом отверстии
Поставим на пути
световой волны ширму с
круглым отверстием
радиуса R.
Определим число зон
Френеля, укладывающихся в отверстии
ширмы.
ab
R rm
m
(a b)
R 1 1
m
b a
2
21
22.
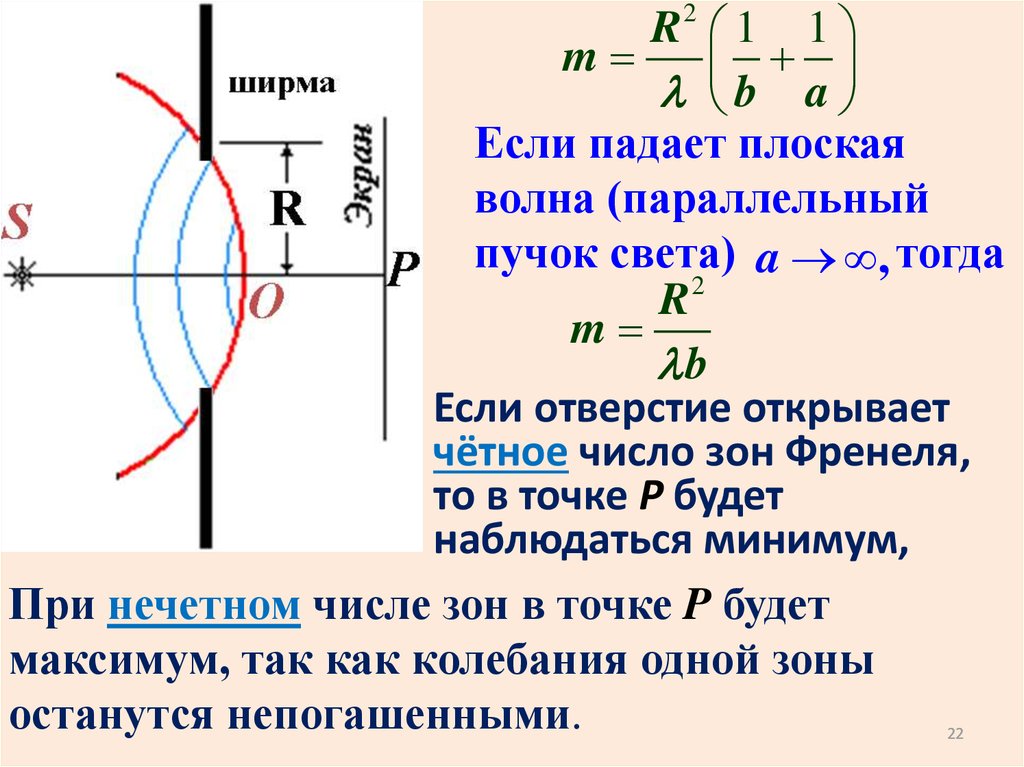
R2 1 1m
b a
Если падает плоская
волна (параллельный
пучок света) a , тогда
2
R
m
b
Если отверстие открывает
чётное число зон Френеля,
то в точке P будет
наблюдаться минимум,
При нечетном числе зон в точке P будет
максимум, так как колебания одной зоны
останутся непогашенными.
22
23.
2324. Дифракция на отверстии
Видеоклип «Дифракция на круглом отверстии»24
25. Дифракция света на прямоугольном и круглом отверстиях.
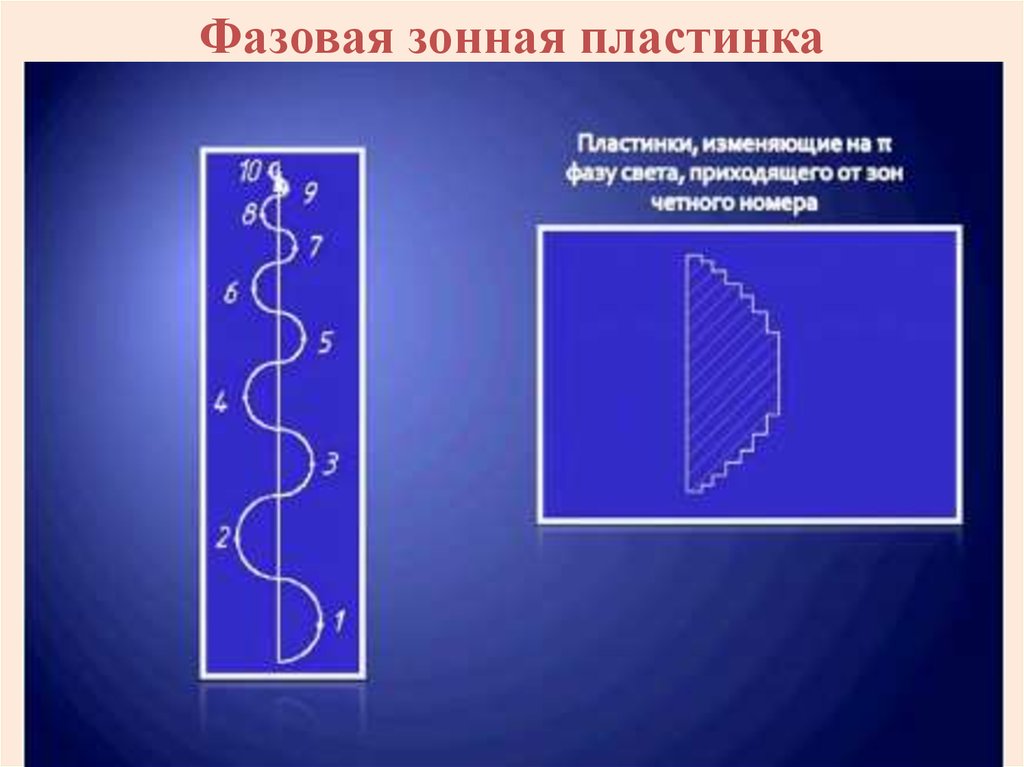
Зонные пластинкиЕсли на пути
световых волн
поставить
пластинку,
которая
перекрывает
все четные
зоны, то интенсивность света в точке P
резко возрастает. Амплитуда в этой точке
равна сумме амплитуд от нечетных зон:
A=A1+A3+A5+... Такая пластинка называется
зонной.
26
26.
Фазовая зонная пластинка27
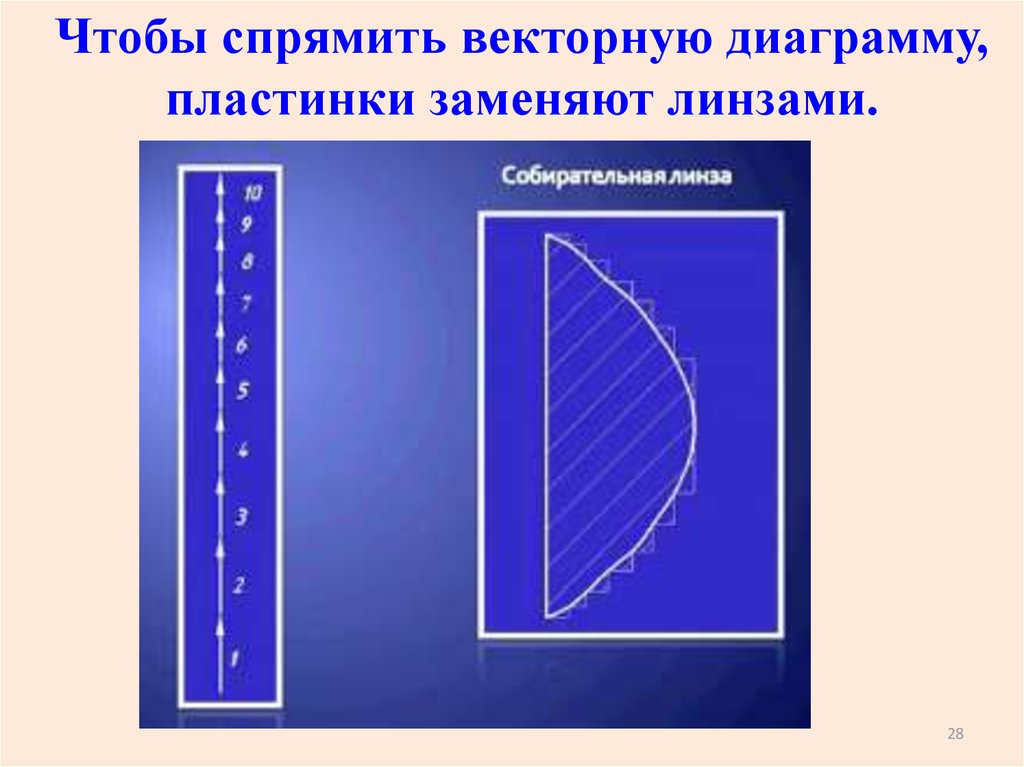
27.
Чтобы спрямить векторную диаграмму,пластинки заменяют линзами.
28
28.
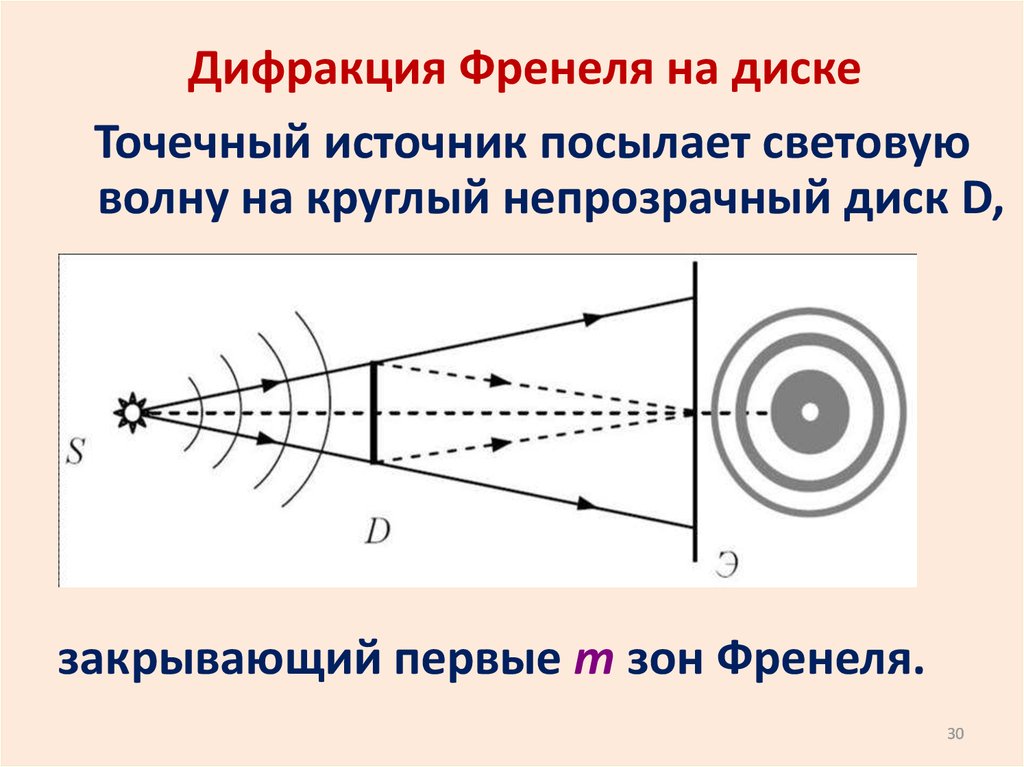
2929.
Дифракция Френеля на дискеТочечный источник посылает световую
волну на круглый непрозрачный диск D,
закрывающий первые m зон Френеля.
30
30. Дифракция Френеля на диске
Если закрыть m первых зон Френеля, тоAm 1
A
.
2
В центре экрана всегда будет
светлое пятно от m+1-й, m+2-ой,
и. т. д. зон.
Это пятно называют
пятном Пуассона.
31
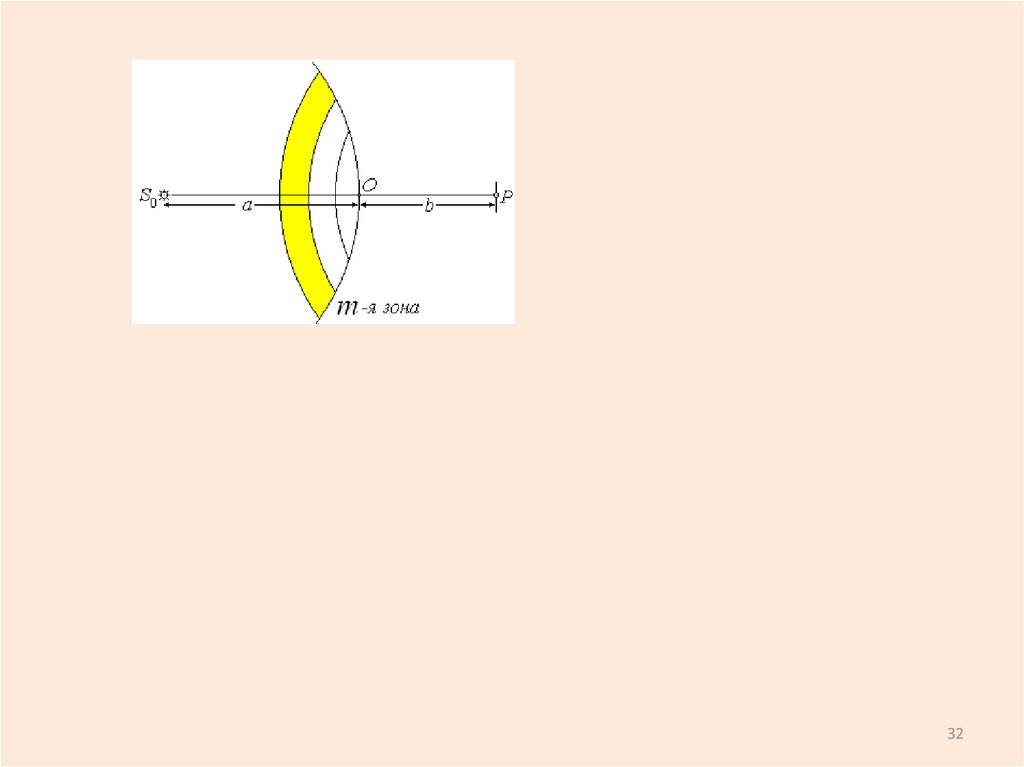
31. Если закрыть m первых зон Френеля, то
3232.
Дифр33
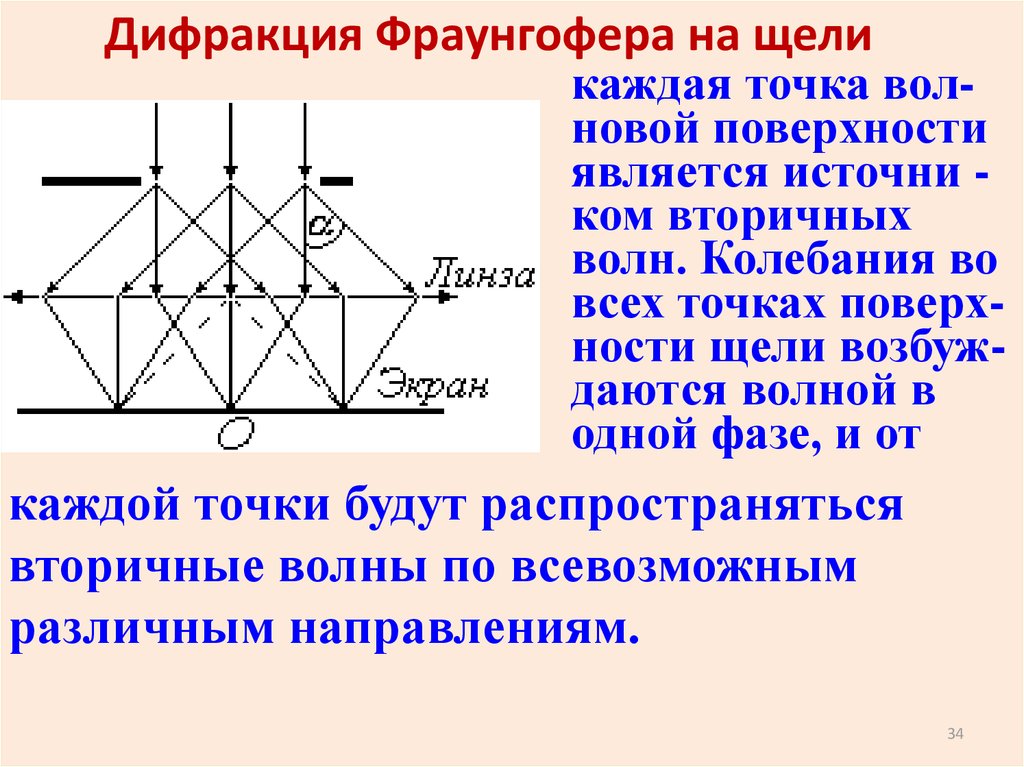
33.
Дифракция Фраунгофера на щеликаждая точка волновой поверхности
является источни ком вторичных
волн. Колебания во
всех точках поверхности щели возбуждаются волной в
одной фазе, и от
каждой точки будут распространяться
вторичные волны по всевозможным
различным направлениям.
34
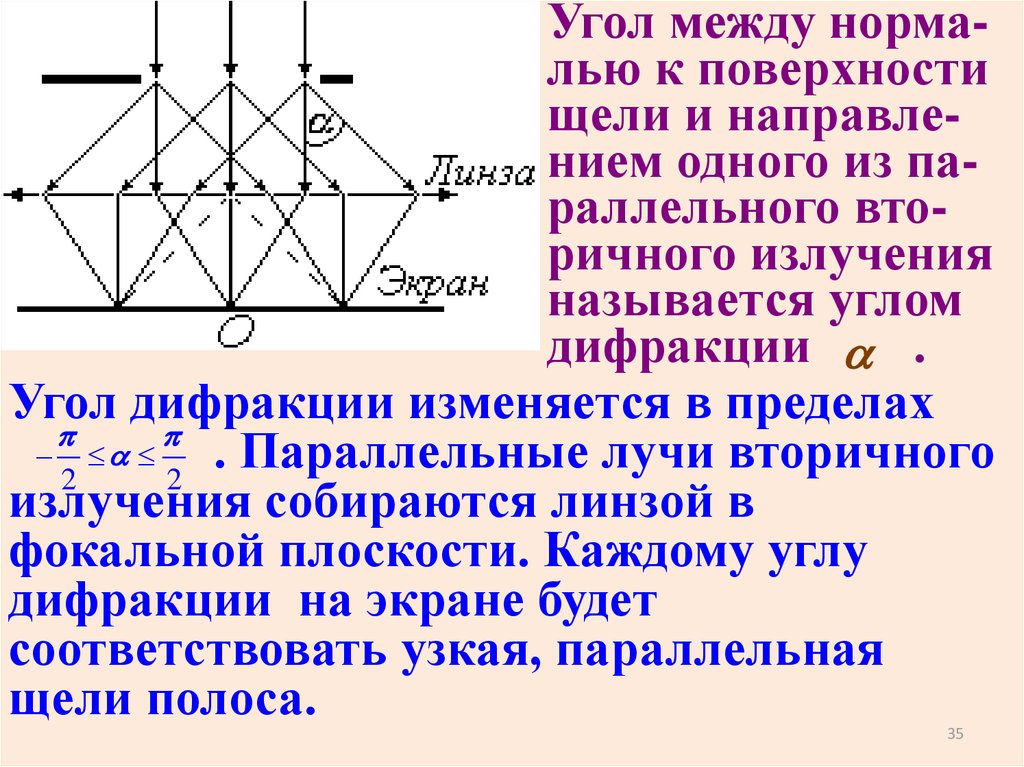
34.
Угол между нормалью к поверхностищели и направлением одного из параллельного вторичного излучения
называется углом
дифракции .
Угол дифракции изменяется в пределах
.
Параллельные
лучи
вторичного
2
2
излучения собираются линзой в
фокальной плоскости. Каждому углу
дифракции на экране будет
соответствовать узкая, параллельная
щели полоса.
35
35.
Щель разбивается на очень большое числоодинаковых, узких полосок параллельных
ребру щели, так чтобы колебания в точке
P, вызываемые вторичными волнами от
всех точек одной полоски, имели почти
одинаковую фазу.
36
36.
D b sinИз тр-ка
D
b sin
D
D
b sin ;
ОСВ
2
D
A
D
A 2 R sin
R sin
;
2
2
2
2
2
37
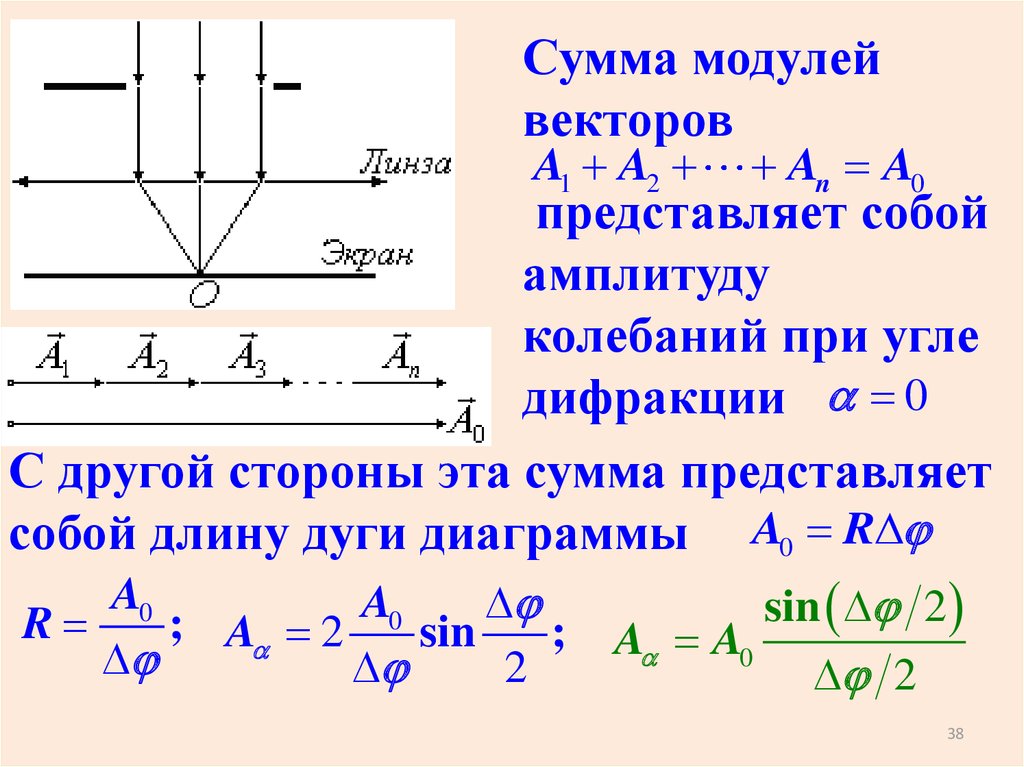
37.
Сумма модулейвекторов
A1 A2
An A0
представляет собой
амплитуду
колебаний при угле
дифракции 0
С другой стороны эта сумма представляет
собой длину дуги диаграммы A0 RD
A0
A
D
0
R
; A 2
sin
;
D
D
2
A A0
sin D 2
D 2
38
38.
A A0I I 0
sin D 2
D 2
2
sin ( D 2)
D 2
2
Учитывая, что I
A2
D
b sin , то
Так как
2
sin b sin
I I 0
2
b sin
2
39
39.
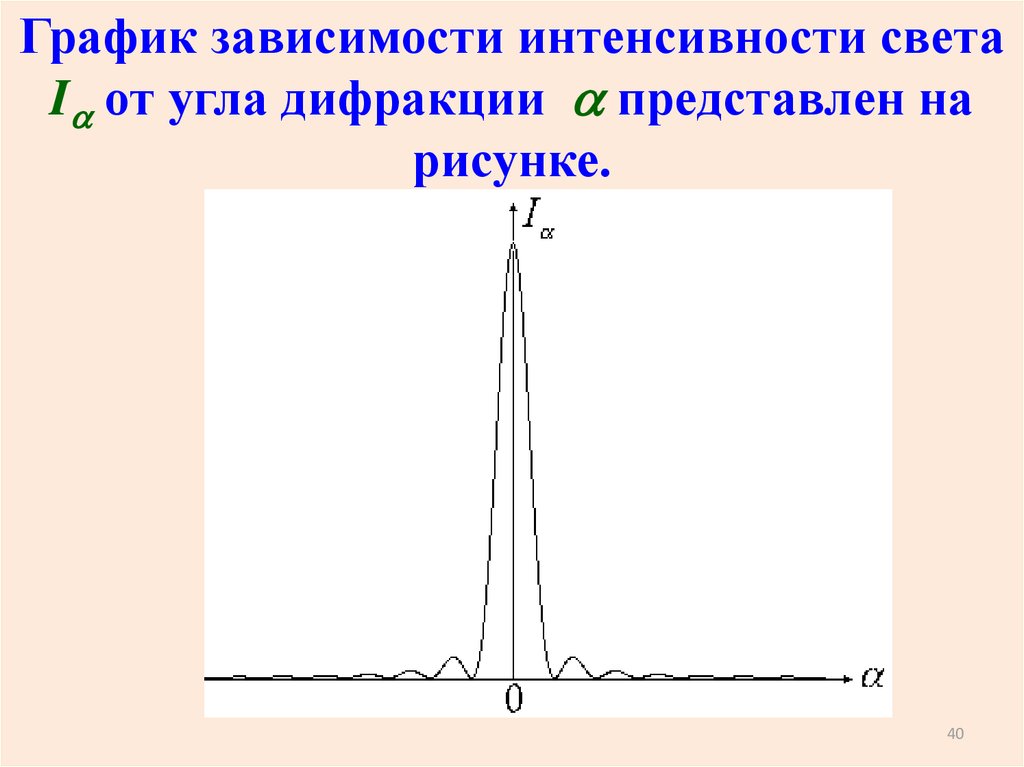
График зависимости интенсивности светаI от угла дифракции представлен на
рисунке.
40
40.
Углы дифракции, которым соответствуютминимумы, и максимумы интенсивности
sin D 2
sin D 2 0
A A0
I 0, если
D 2
D 2 0
То есть когда D 2 m , где m = 1, 2, 3…
D
Учитывая, что
b sin , получим
2
b sin m ;
Условие минимума
b sin m ,
где m = 1, 2, 3…
Если m = 0 возникает центральный
максимум при угле дифракции = 0.
41
41.
Другие максимумы возникают привыполнении условия
D 2 ( 2m 1) , где m = 1, 2, 3…
2
D
b sin , тогда
b sin ( 2m 1)
2
2
То есть другие максимумы возникают
при выполнении условия
b sin ( 2m 1) ,
2
где m = 1, 2, 3…
42
42.
Разобьем щель на зоны Френеля.Разность хода лучей, идущих от краев
каждой зоны равна /2. Тогда
b sin k
2
43
43.
• При четном числе зон (k=2m)онипопарно гасят друг друга. Получим
условие минимума:
b sin m , m 1, 2, 3...
• При нечетном k = 2m - 1 колебания
одной из зон не будут погашены,
получим условие максимума:
b sin (2m 1)
2
, m 1, 2, 3...
44
44.
Дифракционная решёткаВеличина
d a b
называется
постоянной,
или периодом
дифракцион ной решётки,
где a—щирина непрозрачного
промежутка, b — ширина щели
45
45.
При углах дифракции соответствующимнулевым интенсивностям при дифракции
на одной щели наблюдаются главные
минимумы дифракционной решётки. .
b sin m ,
где m = 1, 2, 3…
46
46.
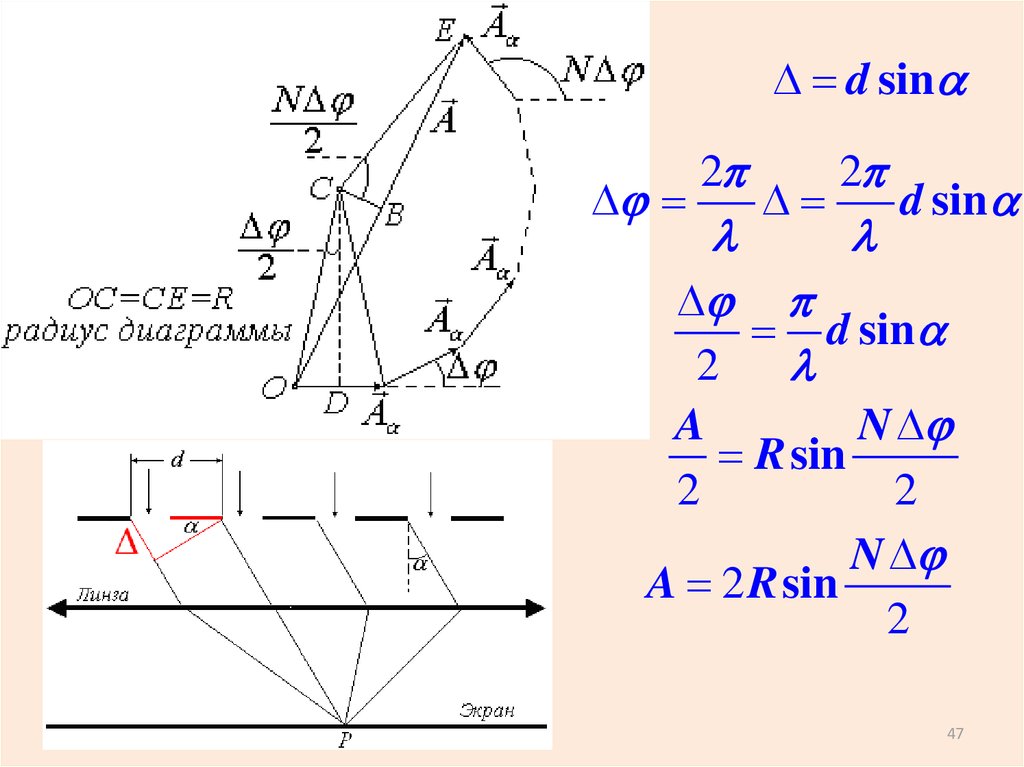
D d sinD
2
D
D
2
d sin
d sin
2
A
N D
R sin
2
2
N D
A 2 R sin
2
47
47.
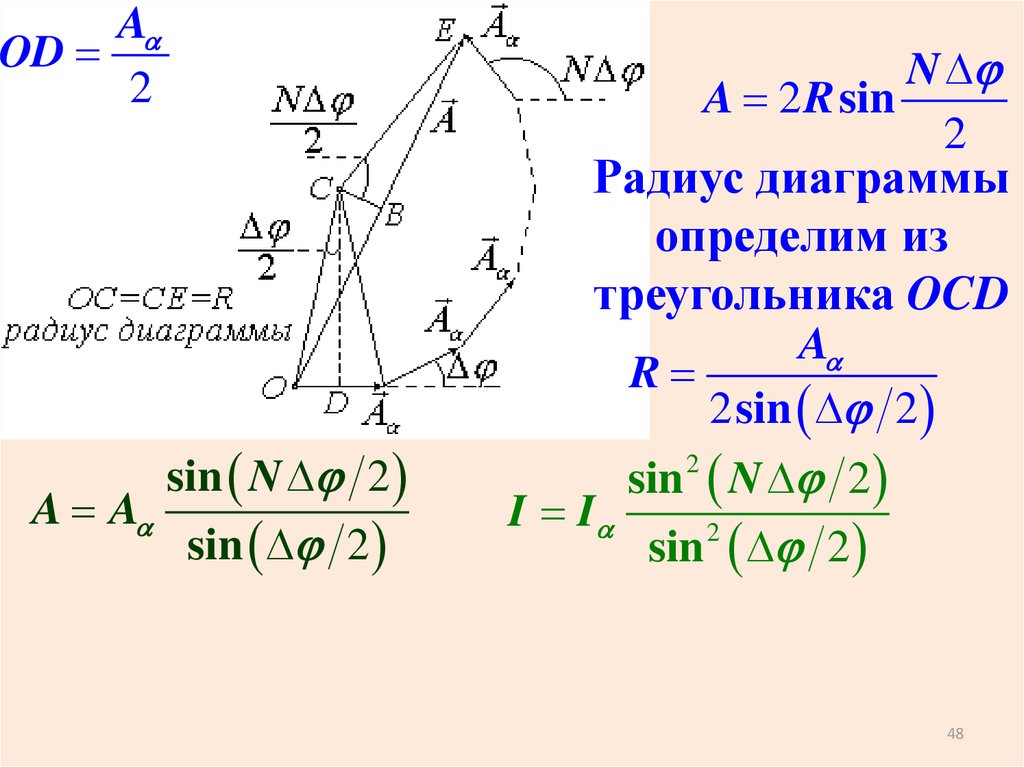
AOD
2
N D
A 2 R sin
2
Радиус диаграммы
определим из
треугольника OCD
A A
sin N D 2
sin D 2
A
R
2 sin D 2
sin N D 2
2
I I
sin 2 D 2
48
48.
sin N D 22
I I
sin D 2
2
sin b sin
,
I
I
Учитывая, что
0
2
b sin
D
получим
d sin ,
2
2
2
sin b sin sin N d sin
I I0
2
2
sin
d
sin
b
sin
2
49
49.
Приведем график интенсивности I от угладифракции для дифракционной решётки,
состоящей из 4-х щелей.
50
50.
Для анализа максимумов и минимумовиспользуем соотношение
I I
sin 2 N D 2
sin D 2
2
Когда D 2 m
интенсивность принимает максимальное
значение I NI , D 2m ( колебания
от всех щелей приходят в одной фазе)
D
d sin , и D 2 m
Учитывая, что
2
Получим условия максимумов
d sin m ,
d sin m ,
где m = 0, 1, 2, 3…
51
51.
Между главными максимумами находятсяN-1 дополнительных минимумов и N-2
дополнительных максимумов — малой
интенсивности.
sin N D 2
2
I I
sin D 2
2
построим графики числителя sin N D 2
и знаменателя sin 2 D 2 интенсивности в
зависимости от величины D 2
.
2
52
52.
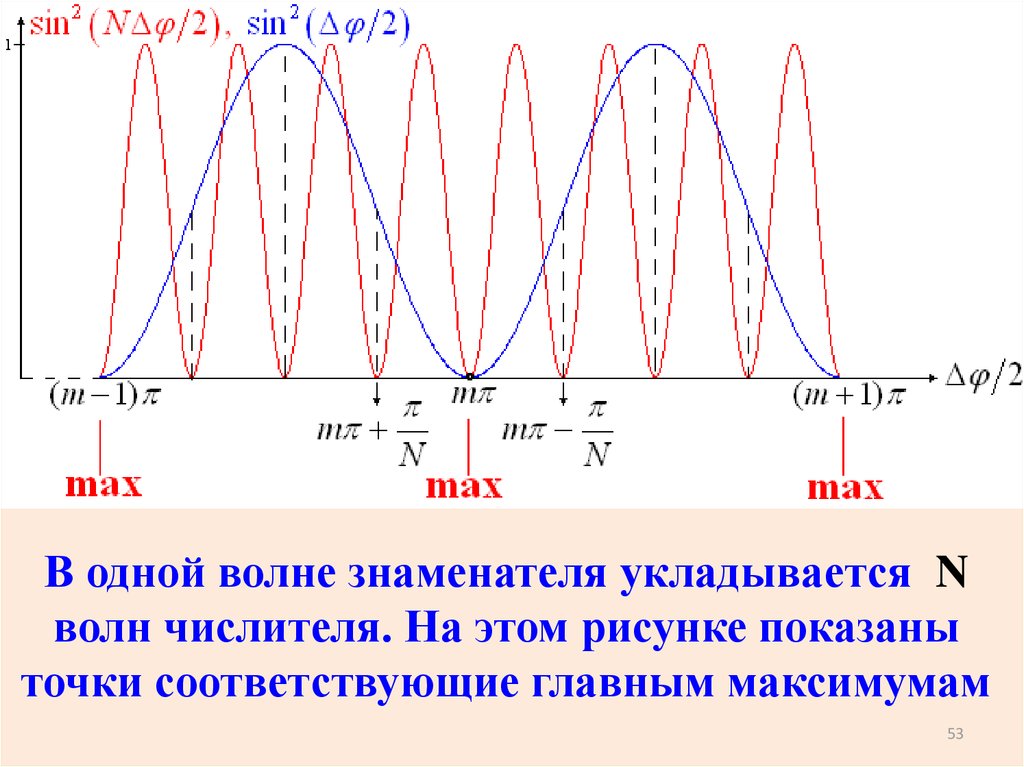
В одной волне знаменателя укладывается Nволн числителя. На этом рисунке показаны
точки соответствующие главным максимумам
53
53.
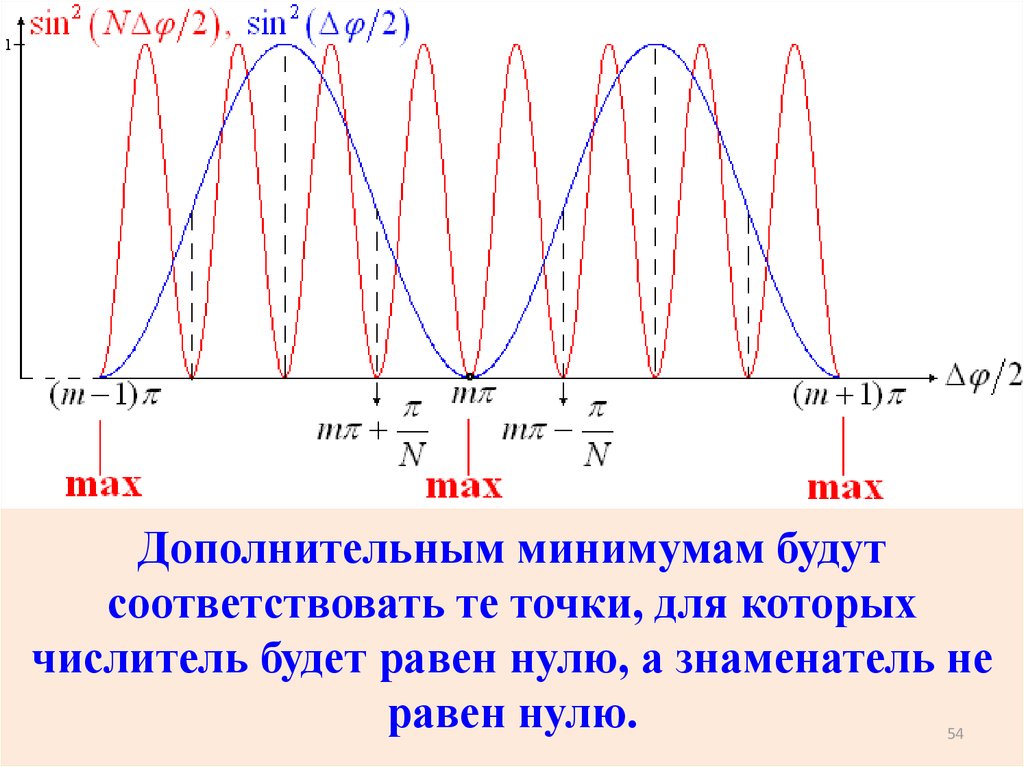
Дополнительным минимумам будутсоответствовать те точки, для которых
числитель будет равен нулю, а знаменатель не
равен нулю.
54
54.
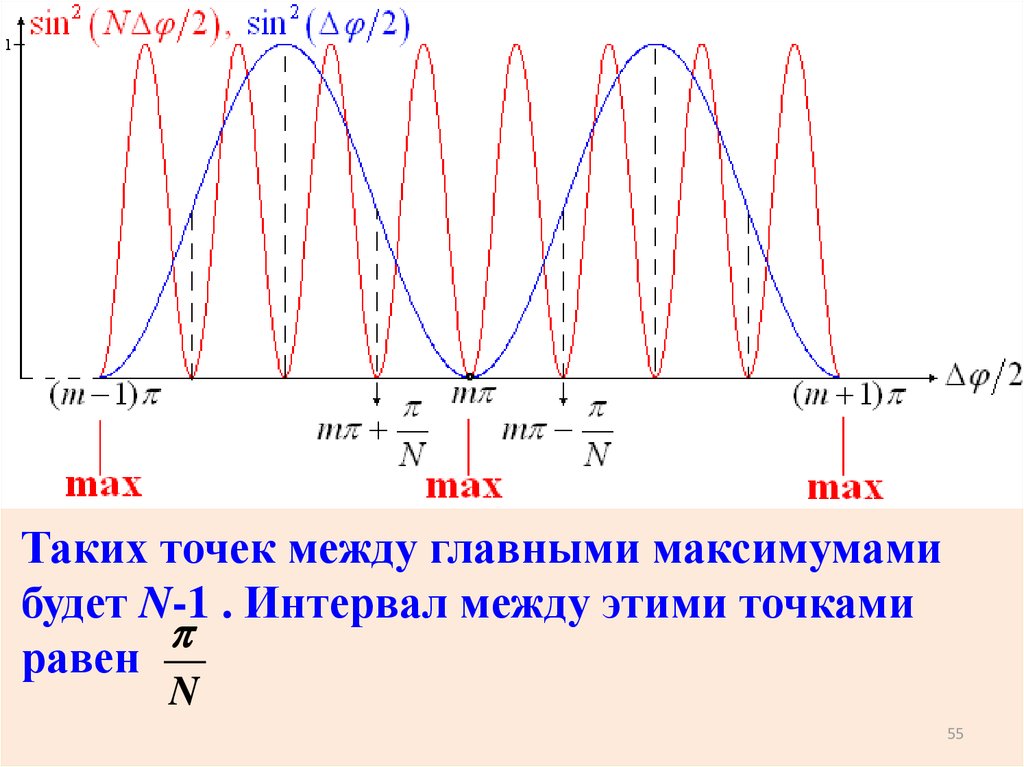
Таких точек между главными максимумамибудет N-1 . Интервал между этими точками
равен
N
55
55.
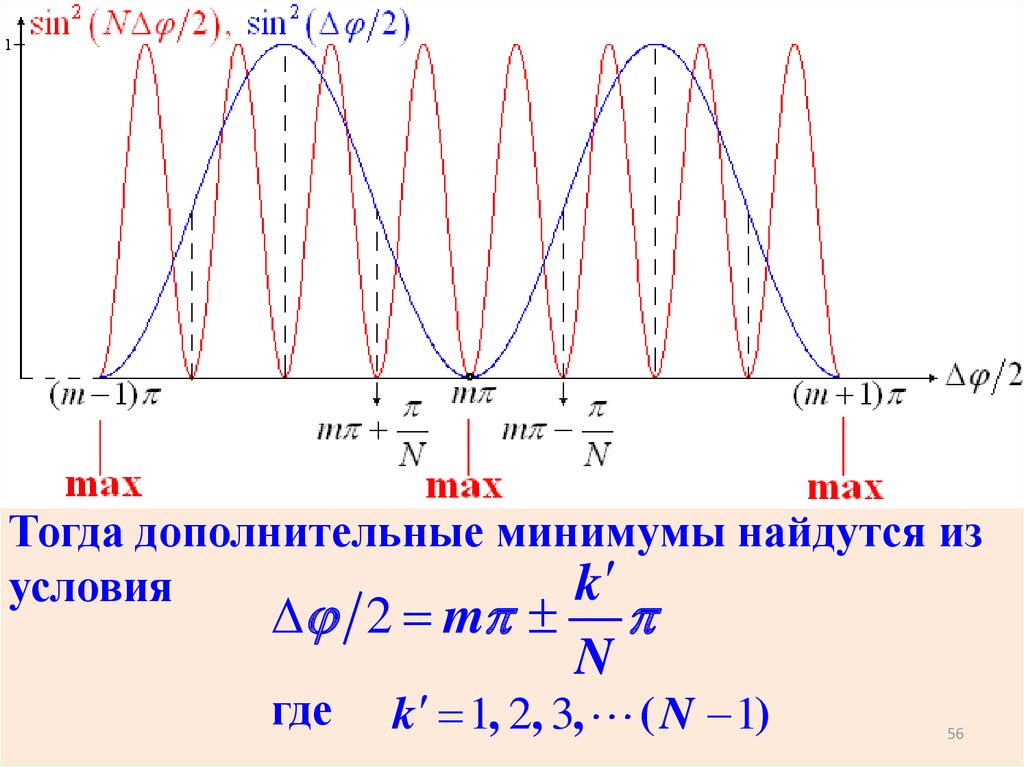
Тогда дополнительные минимумы найдутся изk
условия
D 2 m
где
N
k 1, 2, 3,
( N 1)
56
56.
kD 2 m
N
Учитывая, что D d sin найдём углы
2
дифракции соответствующие дополнительным
,
минимумам дифракционной решётки
k
d sin m
N
, или
k
d sin m где k 1, 2, 3,
N
( N 1)
57
57.
Параметры дифракционной решётки.Угловой дисперсией называется величина
D
где — угловое расстояние между
спектральными линиями, отличающимся
по длинне волны на
продифференцируем
d sin m
m
D
Тогда
d cos m
d cos
,
58
58.
Линейной дисперсией называют величинуDлин
где l — линейное расстояние на экране
между спектральными линиями,
отличающимся по длине волны на .
При небольших углах можно положить
F
Тогда
Dлин FD
59
59.
Разрешающей силой спектральногоприбора называют безразмерную величину
R
где l — минимальная разность длин волн
двух спектральных линий, при которой
эти линии воспринимаются раздельно.
Разрешающая сила дифракционной
решётки пропорциональна порядку
спектра m и числу щелей N, т. е.
R mN
60
60.
Разрешающая способностьобъектива:
R
1
min
D
1, 22
D диаметр объектива
min минимальное угловое
расстояние между двумя точками,
которые видны раздельно
61
61.
Глаз действует как объектив. Роль Dиграет диаметр зрачка глаза dзр.
Полагая dзр = 3 мм, λ = 550 нм, получим
предельное угловое разрешение глаза:
min 1, 22
d зр
47 1
"
'
62
62. Глаз действует как объектив. Роль D играет диаметр зрачка глаза dзр. Полагая dзр = 3 мм, λ = 550 нм, получим предельное угловое
Дифракция рентгеновских лучейРоль дифракционной решетки
могут играть кристаллы.
Дифракцию на кристаллах
наблюдают в рентгеновских
лучах, т.к. нужна маленькая .
63
63.
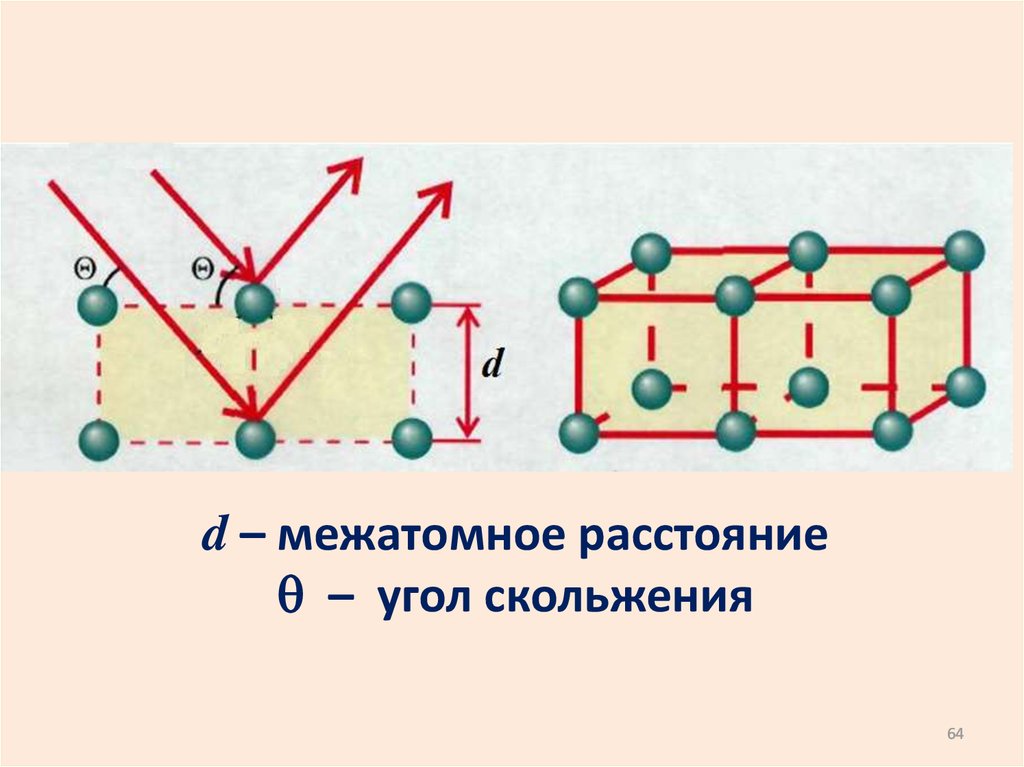
d – межатомное расстояниеq – угол скольжения
64
64.
из треугольникаOAB
D AB BC 2 AB
D 2d sinq
условие максимума
2d sinq m , m 1, 2, ...
получили формулу Вульфа – Брэга.
65
65.
Применение рентгеновской дифракции:1)Рентгеноструктурный анализ.
По известным и q находят межатомные
расстояния и определяют кристаллическую
структуру.
2)Рентгеновская спектроскопия.
По известным d и q находят длину волны.
3)Электронография и нейтронография.
Последняя позволяет определить
магнитную структуру вещества.
66
66.
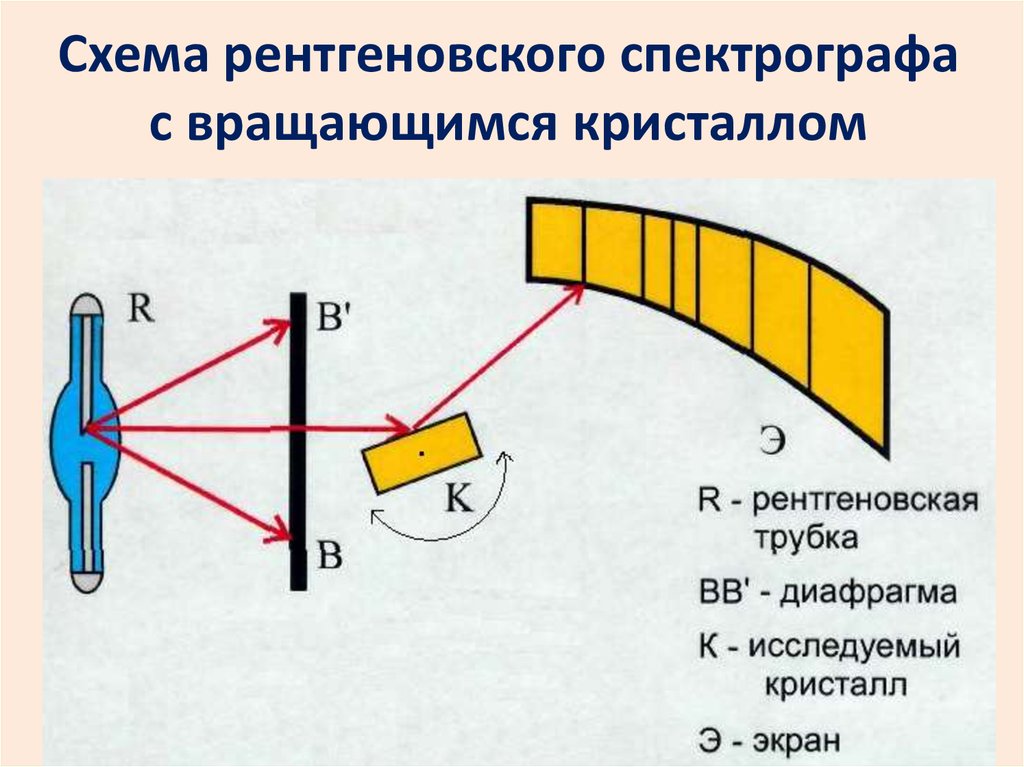
Схема рентгеновского спектрографас вращающимся кристаллом
Дифракция
67
67
67. Схема рентгеновского спектрографа с вращающимся кристаллом
ГолографияПозволяет по дифракционной
картине голограммы
полностью восстановить
объемное изображение
предмета.
68




























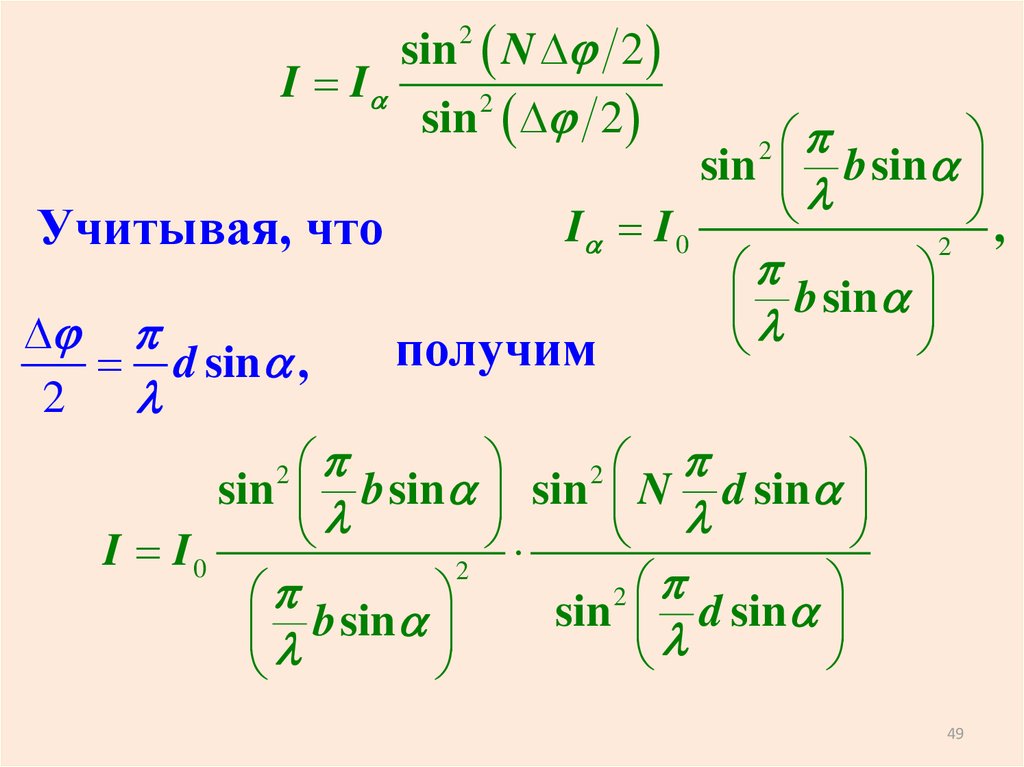













 Физика
Физика








