Линейная алгебра Матрицы. Основные понятия. Действия над матрицами

1. Линейная алгебра

Матрицы. Основные понятия.
Действия над матрицами
Метод обратной матрицы решения систем
линейных уравнений
Метод Гаусса решения систем линейных
уравнений
Ранг матрицы
1

2. Матрицы. Основные понятия

Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a 21
A
a
m1
a12
a 22
am 2
a1n
... a 2n
... amn
...
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов
2

3. Матрицы. Основные понятия

Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Любое число (скаляр) можно представить как матрицу первого
порядка, размерностью 1 1 .
Матрица типа 1 n называется матрица-строка:
a
11
a12 a13 ... a1n
Матрица типа m 1 называется матрица-столбец:
3
a11
a 21
...
a
m1

4. Матрицы. Основные понятия

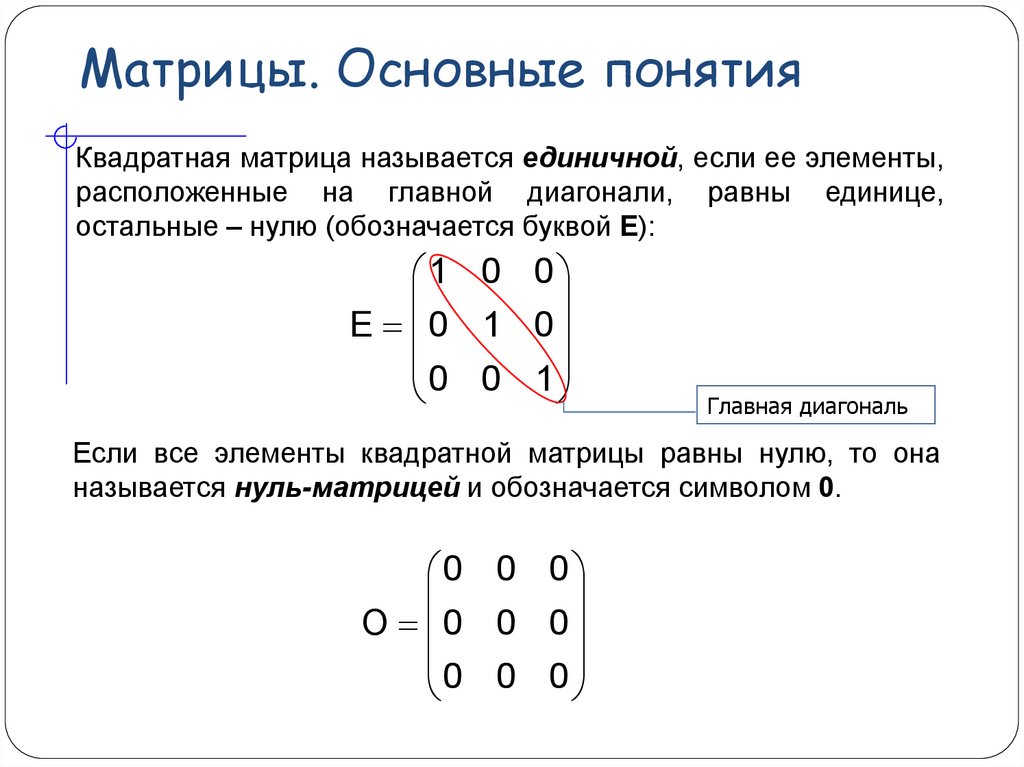
Квадратная матрица называется единичной, если ее элементы,
расположенные на главной диагонали, равны единице,
остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Главная диагональ
Если все элементы квадратной матрицы равны нулю, то она
называется нуль-матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0
4

5. Матрицы. Основные понятия

Для каждой квадратной матрицы n - ного порядка существует
определитель n - ного порядка, элементы которого равны
соответствующим элементам матрицы.
a11 a12
A a 21 a 22
a
31 a 32
a13
a 23
a 33
a11
a12
a13
det A a 21 a 22
a 23
a 31
a 32
a 33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то
называется вырожденной, в противном случае
невырожденная.
матрица
матрица
5

6. Действия над матрицами

Равенство матриц
Матрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dimB;
aij bij
Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
C A B
dim A dimB dimC
c ij aij bij
6

7. Действия над матрицами

Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dimB; bij aij k
Найти значение выражения: C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14
7

8. Действия над матрицами

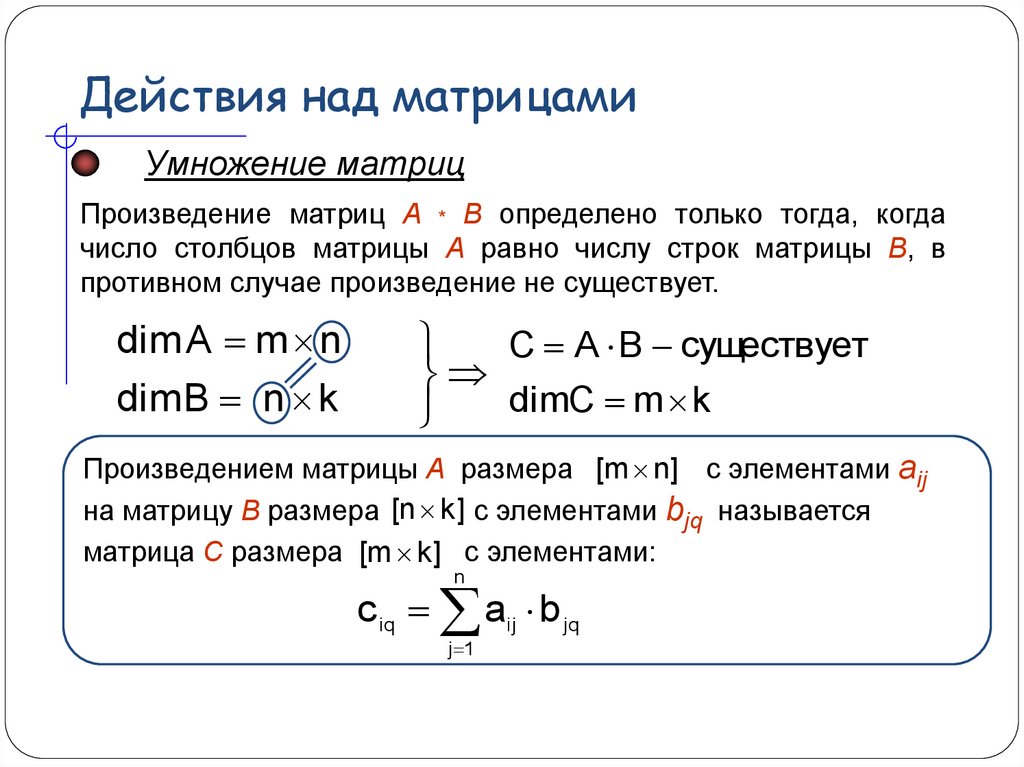
Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij
на матрицу B размера [n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1
8

9. Действия над матрицами

1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
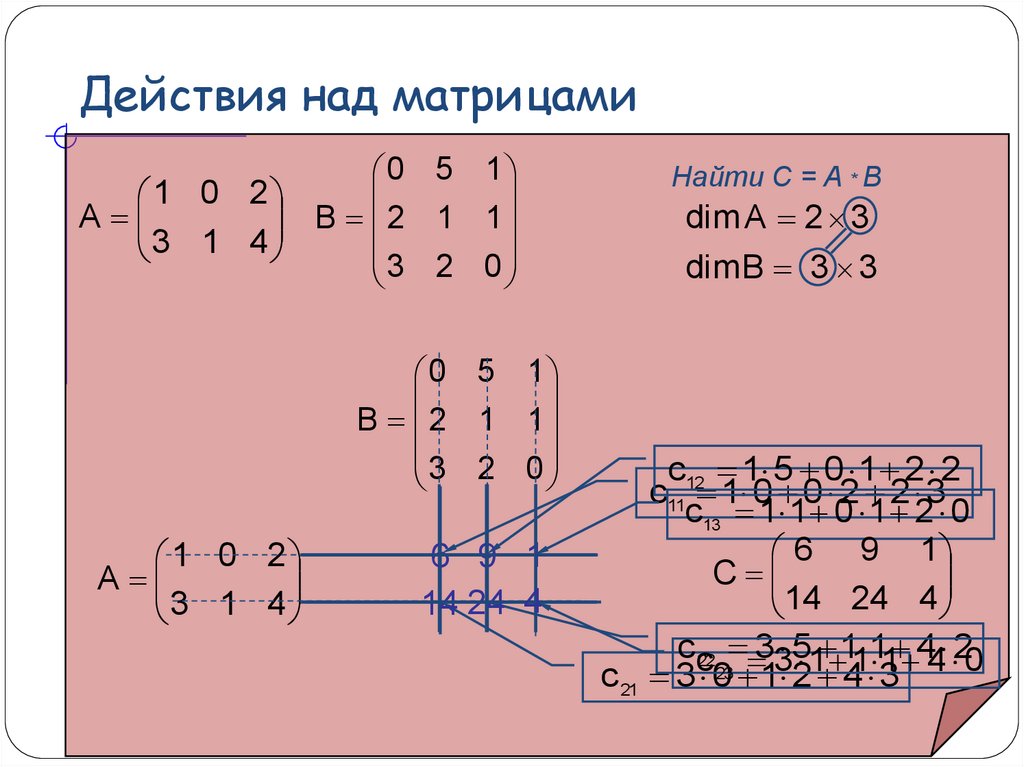
Найти С = A * B
dim A 2 3
dimB 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3
9

10. Действия над матрицами

Свойства операции произведения матриц:
A BC AB C ;
2) AB A B ;
3) A B C AC BC ;
1)
4) В общем случае для произведения матриц не действует
переместительный закон: A B B A
иногда АВ существует, а ВА не имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются коммутативными.
5) Единичная матрица является коммутативной для любой
квадратной матрицы того же порядка:
EA AE A
6) Для двух квадратных матриц А и В одного порядка произведение
определителей равно определителю произведения .
det A det B det AB
10

11. Действия над матрицами

Нахождение обратной матрицы
Обратной матрицей по отношению к данной невырожденной
квадратной матрице A n - ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
11
столбцами

12. Действия над матрицами

0 3 1
0 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2
T
A 2
A 3 4 строки
2 вычтем
строку
1 1 первую
0
-4
2 -1
Разложим
-2 2 определитель
по элементам
3 столбца
6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
0
A
2
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5
11) 1 62 1
12 101 (21
31 22
A
(
1
)
6
3 2
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6
12

13. Метод обратной матрицы решения систем линейных уравнений

Метод обратной матрицы рассмотрим на примере
решения квадратной системы 3 порядка.
a11 x1 a12 x 2 a13 x 3 b1
a 21 x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
32 2
33 3
3
31 1
Запишем эту систему в матричном виде. Обозначим:
a11 a12
A a 21 a 22
a
31 a 32
a13
a 23
a 33
x1
X x2
x3
b1
B b2
b3
Основная матрица
Матрица - столбецМатрица - столбец
системы свободных членов
неизвестных
13

14. Метод обратной матрицы решения систем линейных уравнений

Тогда систему можно записать так:
a11 a12
A X a 21 a 22
a
31 a 32
a13 x1 a11 x1 a12 x 2 a13 x 3 b1
a 23 x 2 a 21 x 1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
a 33 x 3 31 1
3
32 2
33 3
A X B
Найдем решение системы в матричном виде.
Предположим, что det A отличен от нуля и, следовательно,
существует обратная матрица А-1.
Умножим слева матричную запись системы на обратную матрицу:
A 1 A X A 1 B
E X A 1 B X A 1 B
Метод обратной матрицы применим для решения квадратных
14
систем с невырожденной основной матрицей.

15. Метод обратной матрицы решения систем линейных уравнений

Решить систему методом обратной матрицы.
3 x 2 x 3 1
2x1 4 x 2 x 3 2
2x 2x 3
2
1
X A 1 B
1 0 .5
1
1
A 1 1
1
2
3
3
0 3 1
A 2 4 1
2 2 0
x1
X x2
x3
1
B 2
3
1
B 2
3
-0,5
2
-5
0 .5
X 2
5
15

16. Линейная алгебра

Определители второго порядка
Системы из двух линейных уравнений с двумя
неизвестными
Определители n – ого порядка
Методы вычисления определителей
16

17. Определители 2 порядка

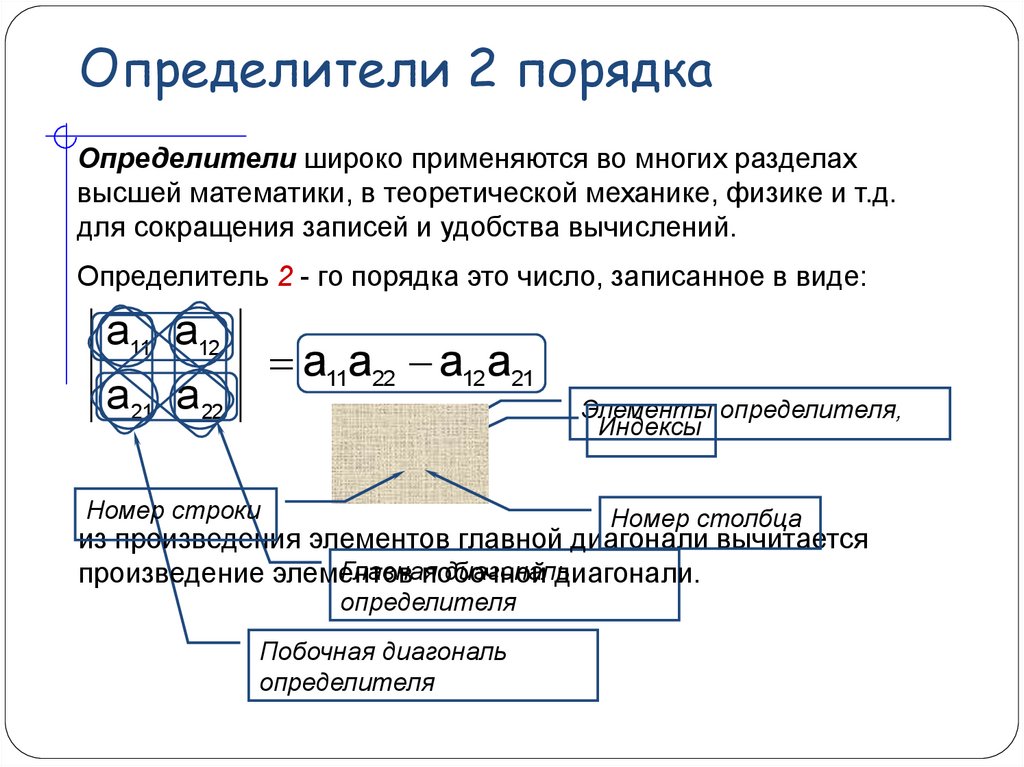
Определители широко применяются во многих разделах
высшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12 a21
a21 a22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя
17

18. Системы из двух линейных уравнений с двумя неизвестными

Центральная задача линейной алгебры - это решение систем
линейных уравнений.
Наиболее простым, является случай, когда число неизвестных n
равно числу уравнений n. Пусть n = 2:
a11x1 a12 x 2 b1
a21x1 a22 x 2 b2
ai j - коэффициенты при неизвестных.
Номер неизвестного,
Номер уравнения
Свободные члены уравнения
Решение данной системы - это пара чисел х1 и х2, которая при
подстановке обращает оба этих уравнения в тождества.
18

19. Системы из двух линейных уравнений с двумя неизвестными

a11x1 a12 x 2 b1
a21x1 a22 x 2 b2
a11 a22 x1 a12 a22 x 2 b1 a22
a12 a21 x1 a12 a22 x 2 a12 b2
a
11
a22 a12 a21 x1 a22 b1 a12 b2
Обозначим:
1
b1 a12
b2 a22
a11 a12
a21 a22
a11 a22 a12 a21
b1 a22 a12 b2
x1 1
19

20. Системы из двух линейных уравнений с двумя неизвестными

Аналогично получим:
обозначив:
2
x 2 2
a11 b1
a21 b2
a11 b2 a21 b1
Система уравнений будет иметь вид:
Если
0
1
x1
;
x1 1
x 2 2
, то решение системы находится по формулам:
2
x2
Вспомогательные
определители системы
Главный определитель
системы
Формулы Крамера
20

21. Системы из двух линейных уравнений с двумя неизвестными

Решить систему методом Крамера:
2x1 x 2 5
3x1 2x 2 3
Вычислим главный и вспомогательные определители системы:
2
21
3 2
2 2 3 1 1
2 5
3 3
1
5 1
3 2
5 2 3 1 7
2 3 3 5 9
Найдем решение системы по формулам Крамера:
7
x 1 7;
1
9
x2
9
1
21

22. Определители n – ого порядка

Определителем n – ого порядка называется число:
a11
a12
a1n
a 21
a 22
a 2n
an1 an 2 ann
Методы вычисления определителей n – ого порядка рассмотрим
на примере вычисления определителей третьего порядка.
22

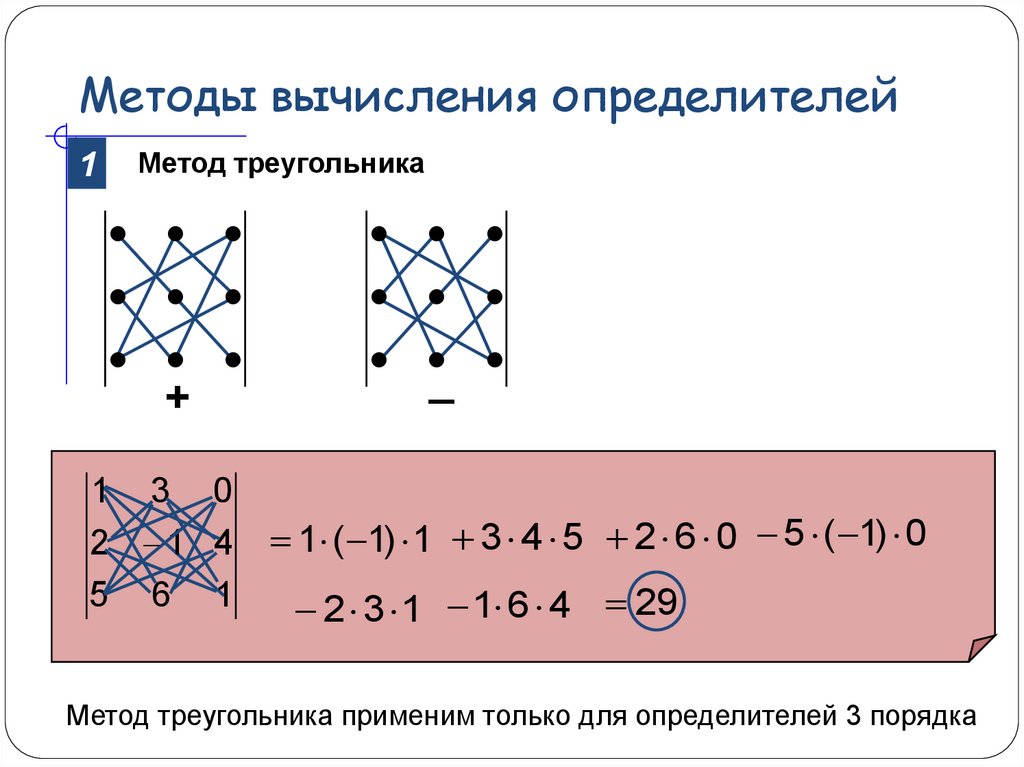
23. Методы вычисления определителей

Метод треугольника
1
+
1
3
0
2 1 4
5
6
1
_
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей233 порядка

24. Методы вычисления определителей

2
Метод разложения определителя по элементам строки
(столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания i - й строки и j - го столбца, т.е.
строки и столбца, на пересечении которых стоит элемент
называется минором элемента и обозначается
Алгебраическим дополнением элемента
Ai j Mi j ( 1)i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
ai j
ai j
Mi j
называется
aa2211 aa2312
MM1123
aa3231 aa3332
1 1 2 3
A
M
(
M
A11 23 M11 23( 1) 1) M
24 23
11

25. Методы вычисления определителей

Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
3 1
0 1
0 3 1 2
( 1)
( 1) 1
2 1
5
1
2 5 1
1 1
1 2
0
0 3
2 5
2 (3 1 5 1) 1 (0 1 2 1) 2
25
( 1)1 3

26. Методы вычисления определителей

3
Использование свойств определителя
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
a21 a22
0 a22 0 a21 0
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0
26

27. Методы вычисления определителей

меняет знак, если поменять местами строки (столбцы):
a11 a12
a21 a22
a11 a22 a12 a21 a12 a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22
27

28. Методы вычисления определителей

не меняется, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a 21 ka11 a 22 ka12
a11a 22 a 21a12
a11a 22 a11ka12 a 21a12 ka11a12
a11 a12
a 21 a 22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a 22 a 23 a11a 22 a 33
0 0 a 33
28

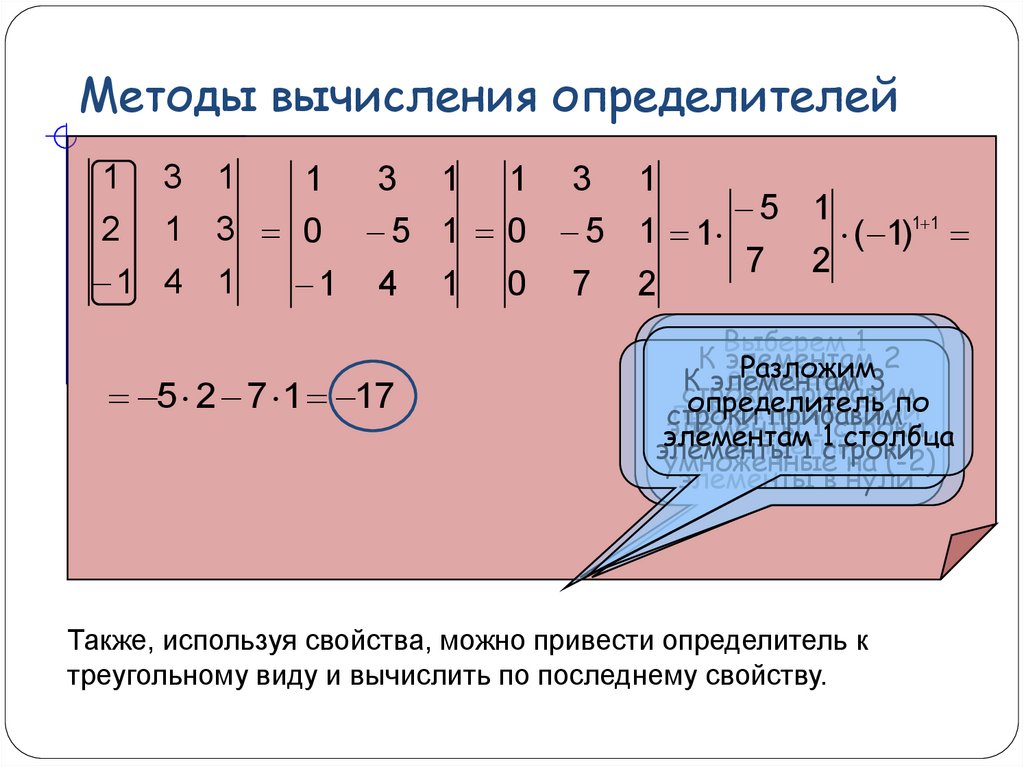
29. Методы вычисления определителей

1
3 1
1
3
1
1
3
1
5 1
1 3 0 5 1 0 5 1 1
7
1 4 1
1 4 1 0 7 2
2
5 2 7 1 17
2
( 1)1 1
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.
29

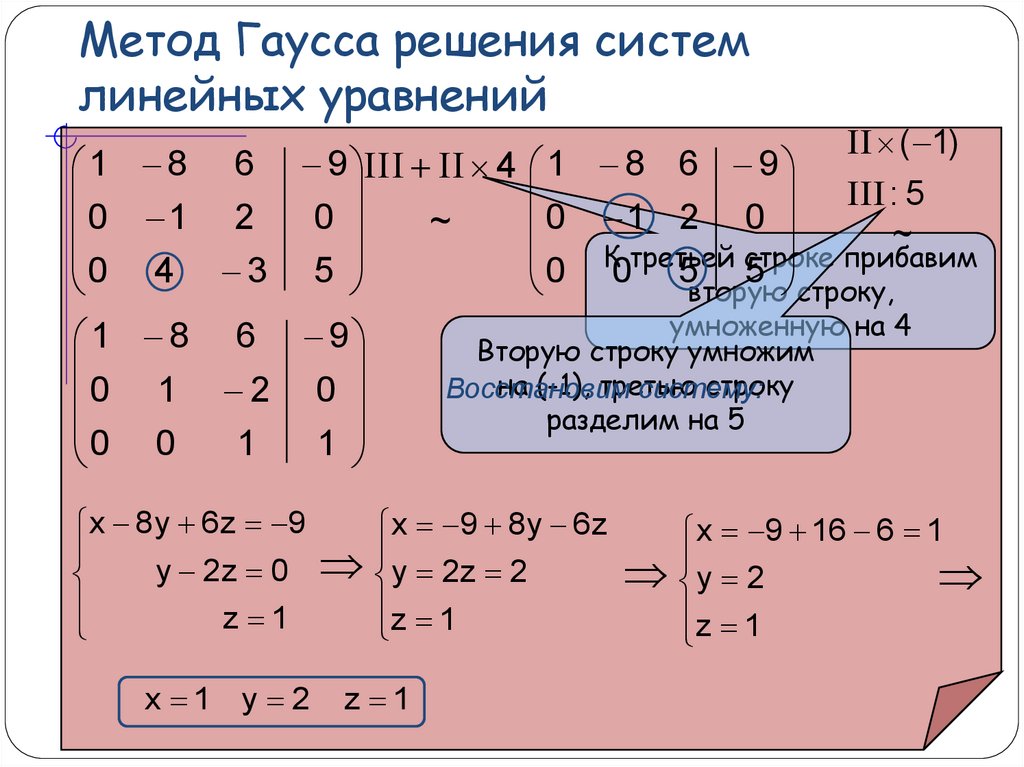
30. Метод Гаусса решения систем линейных уравнений

Рассмотрим задачу решения системы линейных уравнений
размерностью (m x n). Запишем систему в матричном виде: A X B
a11 a12 a13 a1n x1 b1
a 21 a 22 a 23 a 2n x 2 b 2
a a a a x b
mn n
m
m1 m 2 m 3
b1
a11 a12 a13 a1n
a21 a22 a23 a2 n b2
B A B
a a a a b
m
mn
m1 m 2 m 3
Если закрепить раз и
навсегда нумерацию
неизвестных, то можно
опустить неизвестные в
записи системы и
записать ее в виде
матрицы, отделяя
столбец свободных
членов вертикальной
чертой.
Расширенная матрица
системы
30

31. Метод Гаусса решения систем линейных уравнений

Следующие действия над расширенной матрицей системы
называются элементарными преобразованиями.
Умножение или деление элементов строк на одно и то же
число, не равное нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
Конечной целью элементарных преобразований является
получение верхнетреугольной матрицы, у которой все элементы,
стоящие под главной диагональю равны нулю. Преобразования
стараются производить так, чтобы на главной диагонали
появлялись единицы.
a11 a12
a 21 a 22
a
31 a 32
a13
a 23
a 33
b1
b2
b 3
1 c 12
0 1
0 0
c 13
c 23
1
d1
d2
d3
31

32. Метод Гаусса решения систем линейных уравнений

5 x 2y 4z 5
2x 3 y z 7
3 x y 2z 3
Ко второй строке
Запишем
прибавим третью строку,
расширенную
умноженную на (-5)
матрицу системы
( 2)
5 2 4 5 ( 2) 1 8 6 9 ( 3)
~
1 строке
7 прибавим
2 К3первой
~
2 3 1 7
строку,
3 1 вторую
3 1 2 3
2
3
на (-2)
умноженную
6
9 1Ко второй
8
6строке
9 ( 5)
1 8
прибавим
первую
строку,
вычтем
Из третьей строки
0 19 13на (-2),
25
~
0 19 13 25 ~ умноженную
вторую строку
строке
0 23 16 30
0 К третьей
4 первую
3 строку,
5
прибавим
умноженную на (-3).
32

33. Метод Гаусса решения систем линейных уравнений

1 8 6 9 4
0
~
0 1 2
0 4 3 5
x 1 y 2
1 8 6 9
: 5
0 1 2 0
~
строке
0 К0третьей
прибавим
5
5
вторую строку,
умноженную на 4
Вторую строку умножим
на (-1), третью
строку
Восстановим
систему:
разделим на 5
1 8 6 9
0 1 2 0
0 0
1
1
x 8 y 6 z 9
y 2z 0
z 1
( 1)
x 9 8 y 6 z
y 2z 2
z 1
x 9 16 6 1
y 2
z 1
z 1
33

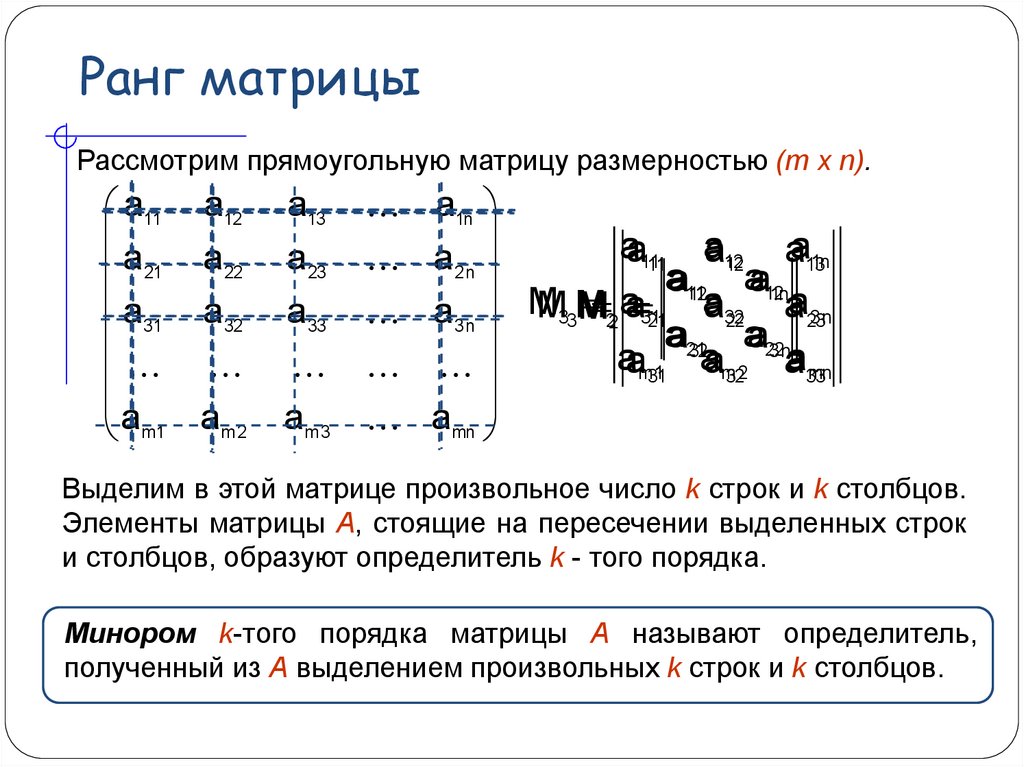
34. Ранг матрицы

Рассмотрим прямоугольную матрицу размерностью (m x n).
a11 a12
a 21 a 22
a
a 32
31
am1 am 2
a13
a 23
a 33
am3
a1n
aa1111 a12 aa131n
a 2n
a1112 aa121n
22aa 3121 a 3222 aa233n
M33M
a3n M
a2132 aa223n
aam311 aam322 a 33mn
amn
Выделим в этой матрице произвольное число k строк и k столбцов.
Элементы матрицы А, стоящие на пересечении выделенных строк
и столбцов, образуют определитель k - того порядка.
Минором k-того порядка матрицы А называют определитель,
полученный из А выделением произвольных k строк и k столбцов.
34

35. Ранг матрицы

Рангом матрицы называется наибольший порядок отличного от
нуля минора этой матрицы.
2 3 4 5
A 0 2 3 1
0 2 2 4
2
18 миноров 2 - го порядка, например:
3
0 2
4
0 2 3 20
Матрица А имеет 4 минора 3 - его порядка,
например:
2
3
0
2
2
4
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r ( A ) 3
35

36. Ранг матрицы

Определитель, порядок которого равен рангу матрицы, называется
базисным минором. Он может быть не единственным.
Можно показать, что эквивалентные преобразования не меняют
ранга матрицы. Поэтому, когда требуется вычислить ранг матрицы,
ее приводят к треугольному виду.
Ранг матрицы равен числу ненулевых строк матрицы,
приведенной к треугольному виду
1 3 2
A 0 5 4 ~
1 7 6
1 3 2 ( 2)
0 5 4
~
0 10 8
r( A ) 2
1 3 2
0 5 4
0 0 0
36

37. Векторная алгебра

Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
37

38. Скалярное произведение векторов

Пусть постоянная сила F действует на прямолинейно
перемещающуюся точку М под углом φ к направлению движения
Как известно из физики, работа силы F по
перемещению точки М определяется по
формуле:
A F S cos
F
М
S
Таким образом, двум векторам: силе и перемещению оказался
сопоставлен скаляр – работа.
Этот скаляр А и называется скалярным произведением силы
перемещение S
F на
Скалярным произведением двух векторов называется
произведение модулей этих векторов на косинус угла между ними..
38

39. Скалярное произведение векторов

Скалярное произведение двух векторов
a и b обозначатся:
a b a b cos
Если векторы
a и b не нулевые:
a b 0
ПР
cos
a a b
a b a bПР
cos
b b aПР
b
a
a a a a cos 0o
a a
2
2
a b
ПРb a
Скалярный квадрат
вектора
равен
квадрату его модуля:
Законы скалярного произведения
1) a b b a
2)
(a b ) c a c b c
3) (a b ) ( a ) b a ( b )
39

40. Скалярное произведение векторов

Для координатных ортов декартовой системы координат
справедливо:
i i j j k k 1
i j i k j k 0
Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
Найдем скалярное произведение:
a b x1 i y1 j z1 k x2 i y 2 j z2 k
k0 i y z 0j k z z k1
x1x2 i12 y1x2 i0 j z1x2 i 0 k x1y 2 j0 i y1y 2 j12
z1y 2 0
j k x1z2
2
1 2
1 2
a b x1 x2 y1 y 2 z1 z2
40

41. Скалярное произведение векторов

Из формулы скалярного произведения векторов следует формула
для нахождения угла между векторами:
a b
cos
a b
x1 x 2 y 1 y 2 z1 z2
x12 y 12 z12 x 22 y 22 z22
Найти косинус угола между векторами:
a b 1 6 2 4 3 2 8
a i 2 j 3k
b 6i 4 j 2k
a 12 22 3 2 14
b 62 42 2 56 2 14
8
2
cos
14 2 14 7
2
41

42. Векторное произведение векторов

левой
Тройка некомпланарных векторов a; b; c называется правой
если наименьший поворот с конца третьего вектора c от первого
вектора a ко второму вектору b виден против
часовой стрелки
по
c
c
b
a
a
c
b
a b
Векторным произведением вектора a на вектор b называется
вектор c , определяемый следующим образом:
c a b sin( a ; b ) .
c a; c b
Вектор
c направлен так, что тройка векторов a; b ; c42- правая.

43. Векторное произведение векторов

Модуль вектороного произведения равен площади
параллелограмма, построенного на перемножаемых векторах
S c a b sin
c
b
a
a b 0
a II b
Законы векторного произведения
1) a b b a
2)
a b c a b a c
3) (a b ) ( a ) b a ( b )
4)
a a 0 - векторный квадрат равен нулю для любого
43 вектора

44. Векторное произведение векторов

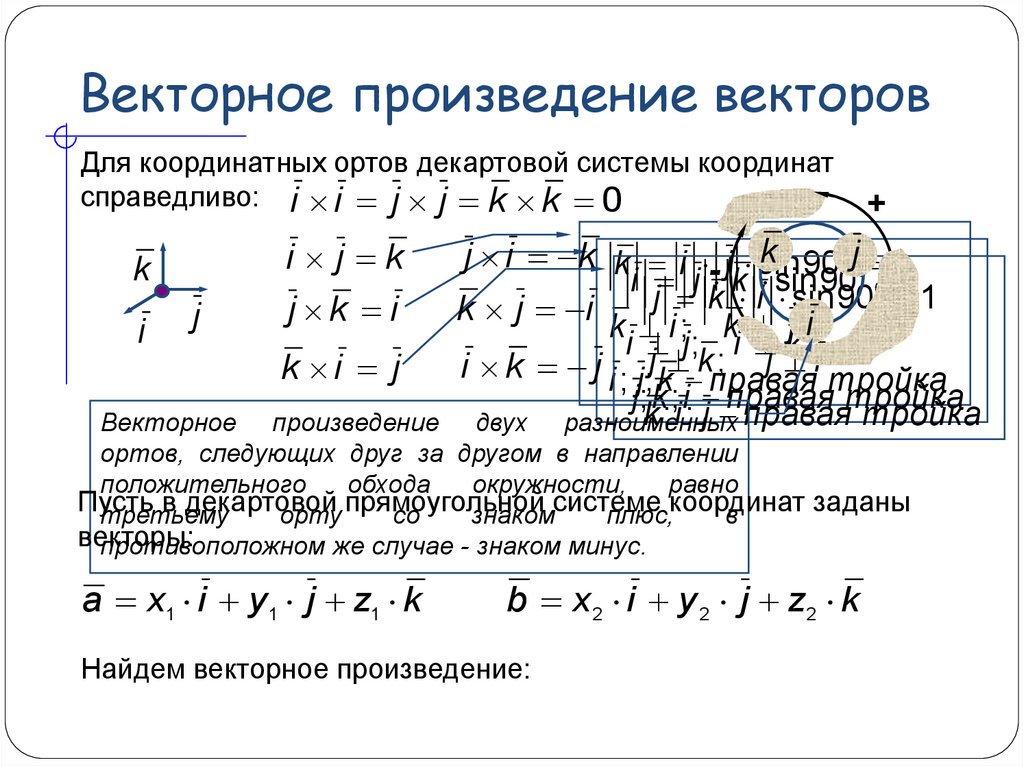
Для координатных ортов декартовой системы координат
справедливо: i i j j k k 0
i j k
k
i
j
j k i
k i j
+
k 90 0 j0 1
j i k k i - j sin
i j k sin 90 0 1
i sin 90 1
k j i k j i ; kk
ji
i j; i k
; j i
i k j i ; j ;jk kправая
тройка
j ; k ; i правая тройка
k ; i ; j правая тройка
двух разноименных
Векторное произведение
ортов, следующих друг за другом в направлении
положительного
обхода
окружности,
равно
Пусть
в
декартовой
прямоугольной
системе
заданы
третьему
орту
со
знаком
плюс,координат
в
векторы:
противоположном же случае - знаком минус.
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
Найдем векторное произведение:
44

45. Векторное произведение векторов

x x i 0 i y x
j ki z x k j i x y i
k j
y y j0 j z y k i j x z i jk
y z ji k z z 0k k
a b x1 i y1 j z1 k x2 i y 2 j z2 k
1
1
2
1
2
1
1
2
2
1
2
1
1
2
1
2
2
2
y1x2 k z1x2 j x1y 2 k z1y 2 i x1z2 j y1z2 i
y1
z1
x1
z1
x1
y1
y2
z2
x2
z2
x2
y2
y1z2 z1y 2 i x1z2 z1x2 j x1y 2 y1x2 k
i
j
k
a b x1 y 1 z1
x 2 y 2 z2
45

46. Векторное произведение векторов

Найти векторное произведение векторов:
a 2i 3 j k
i
j
b 3i j 4k
k
a b 2 3 1
3 1 4
3
1
1 4
i
2
1
3
4
j
2
3
3
1
k
12 1 i 8 3 j 2 9 k 11i 5 j 7k
46

47. Векторное произведение векторов

Найти площадь треугольника с вершинами:
A 2; 3; 1
B 5; 6; 3
C 7; 1; 10
В
Найдем координаты векторов:
AB 5 2; 6 3; 3 1 3; 3; 2
AC 7 2; 1 3; 10 1 5; 2; 9
S
А
С
1
a b
2
i
a b 3
j
k
3
2 31i 17 j 21k
5 2 9
1
1
2
2
2
1691 20.6
S
31 ( 17) ( 21)
2
2
47

48. Смешанное произведение векторов

Векторно - скалярным или смешанным произведением трех
векторов a; b; c называется произведение, которое получается
скалярным умножением векторного произведения двух векторов
на третий вектор, т.е. произведение вида:
a b c
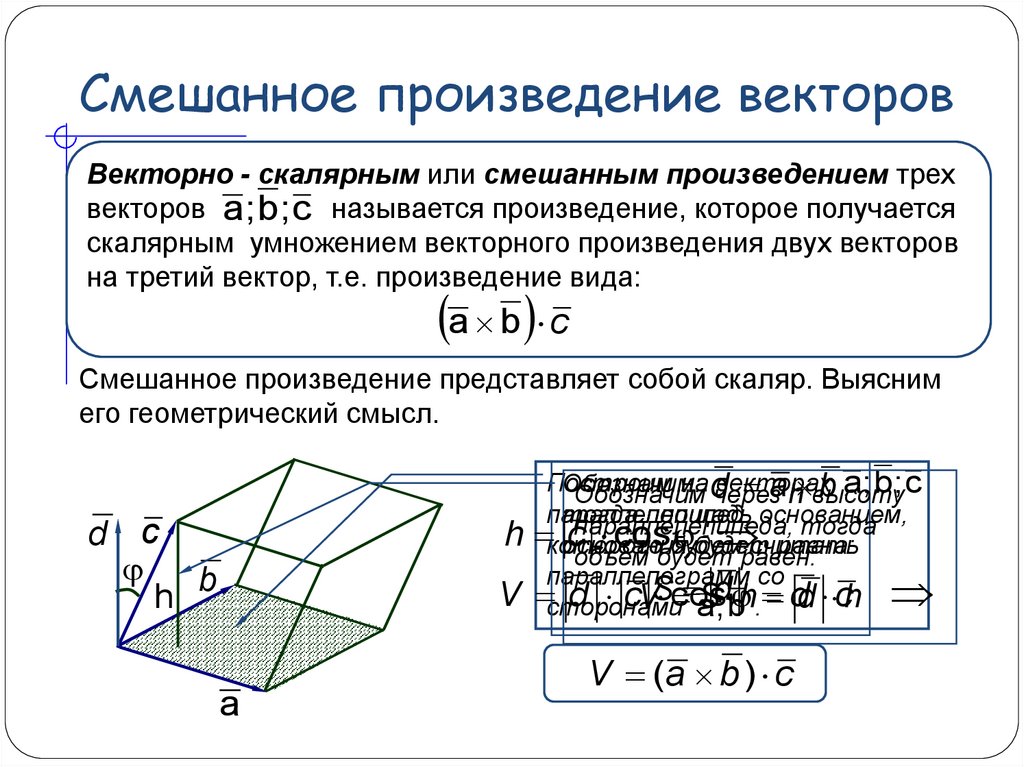
Смешанное произведение представляет собой скаляр. Выясним
его геометрический смысл.
d c
h b
h
V
a
Построим
на d
векторах
Обозначим:
, ; b; c
a h высоту
ba
Обозначим
через
параллелепипед,
тогда
площадь основанием,
параллелепипеда,
тогда
которого
c
cos
будем
считать
основания
будет
равна:
объем будет
равен:
параллелограмм со
сторонами
d cVS cos
a
Sd; b h. dd ch
V (a b ) c
48

49. Смешанное произведение векторов

Смешанное произведение трех векторов равно объему
параллелепипеда, построенного на этих векторах в том случае,
если векторы a; b; c образуют правую тройку векторов (как в
предыдущем примере).
В случае, если векторы образуют левую тройку, то смешанное
произведение равно объему параллелепипеда, взятому со знаком
«-»:
a b c V
Таким образом, объем параллелепипеда, построенного на трех
векторах, всегда равен абсолютной величине их смешанного
произведения:
V a b c
49

50. Смешанное произведение векторов

Законы смешанного произведения
1) Сочетательный закон следует из геометрического
смысла смешанного произведения:
a b c a (b c )
V a (b c )
V a b c
Учитывая сочетательный закон, смешанное произведение
обозначают: (a ; b ; c ) или a b c .
2) Закон круговой переместительности:
a b c b c a c a b a c b c b a b a c
c
b
a
При перестановке множителей не нарушающей их кругового
порядка, смешанное произведение не меняется, при
перестановке же множителей, нарушающей круговой
порядок, смешанное произведение меняет свой знак 50

51. Смешанное произведение векторов

3) Распределительный закон
a
1
a2 b c a1b c a2b c
abc 0
a ; b ; c компланарны
В частности, смешанное произведение равно нулю, если в нем
два множителя одинаковы: a a c 0
Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
c x3 i y 3 j z3 k
51

52. Смешанное произведение векторов

i
j
k
y2
b c x 2 y 2 z2
y3
x3 y 3 z3
a (b c )
y2
z2
y3
z3
x1
z2
z3
i
x2
z2
x3
z3
x2
z2
x3
z3
y1
j
x2
y2
x3
y3
x2
y2
x3
y3
z1
x1 y 1 z1
a b c x 2 y 2 z2
x 3 y 3 z3
52
k

53. Смешанное произведение векторов

Найти объем треугольной пирамиды с вершинами:
A 2; 2; 2 B 4; 3; 3 C 4; 5; 4 D 5; 5; 6
А
Найдем координаты векторов:
AB 4 2; 3 2; 3 2 2; 1; 1
D
AC 4 2; 5 2; 4 2 2; 3; 2
AD 5 2; 5 2; 6 2 3; 3; 4
2 1 1
0
0 1
AB AC AD 2 3 2 2
3 3 4
1
V abc
6
1
2
5 1 4
В
С
2
1
5 1
7
Объем треугольной
7 пирамиды
равен 1/6 части
V параллелепипеда,
6
построенного на векторах
a; b ; c
53