Помехоустойчивое кодирование. Декодирование циклических кодов

1. Помехоустойчивое кодирование

Декодирование циклических
кодов

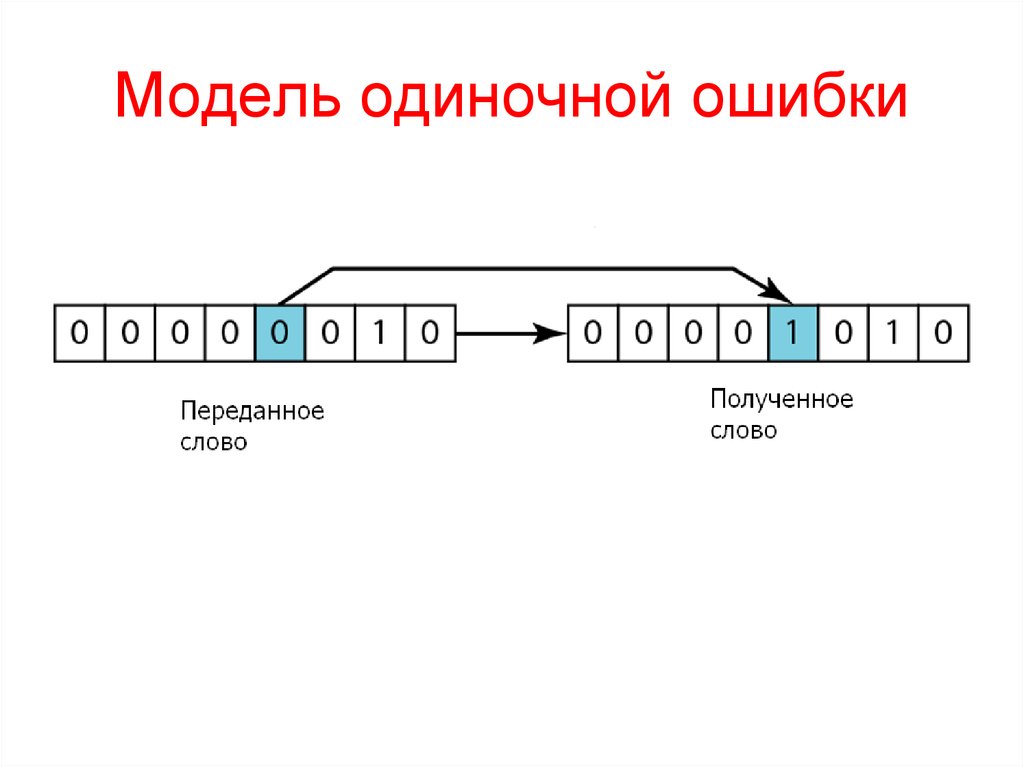
2. Модель одиночной ошибки

3. Модель ошибки

• Пусть c(x) – передаваемый по каналу
многочлен.
• Тогда полученный ошибочный
многочлен
c ( x) c( x) e( x),
e( x) многочлен ошибки

4. Модель ошибки

• Если e(x)=0, то полученный многочлен
без остатка делится на порождающий
многочлен.
• В противном случае
c ( x) b( x) g ( x) s ( x),
s ( x) синдром, deg s ( x) n k

5. Связь между многочленом ошибок и синдромом

с( x) a ( x) g ( x)
с ( x) с( x) e( x)

6. Связь между многочленом ошибок и синдромом

с ( x) с( x) e( x)
с( x) a ( x) g ( x)
с ( x) b( x) g ( x) s( x)
e( x) с ( x) c( x)
b( x ) g ( x ) s ( x ) a ( x ) g ( x )
(a( x) b( x)) g ( x) s( x)

7. Связь между многочленом ошибок и синдромом

• Синдром принятого многочлена равен
остатку от деления многочлена
ошибки на порождающий многочлен.

8. Свойства синдрома циклического кода

• Теорема (Меггитт). Пусть s (x ) - синдром
принятого из канала многочлена с (x ).
Обозначим синдром циклического сдвига x с (x ).
принятого многочлена s (1) ( x) . Тогда
s ( x) x s( x)(mod g ( x))
(1)

9. Алгоритм Меггитта

Получаем остаток от деления е(х), соответствующего ошибке в
старшем разряде [1000000000], на порождающий полином g(x):
r0 ( x) e( x) q( x) g ( x)
Делим полученный полином c(х) на g(x) и получаем текущий
остаток r(x).
Сравниваем r0 ( x) c r ( x)
–
–
Если они равны, то ошибка произошла в старшем разряде.
Если нет, то увеличиваем степень принятого полинома на x и снова
проводим деления: x·c(x) на g(x), остаток опять обозначим r(x)
Опять сравниваем полученный остаток с r0 ( x)
–
–
Если они равны, то ошибки во втором по старшинству разряде.
Если нет, то берем х · х ·c(х) · и повторяем эти операции до тех пор,
пока r(x) не будет равен r ( x)
0