Тепломассообмен. Сложный теплообмен -2

1. ТЕПЛОМАССООБМЕН

Сложный теплообмен
Лекция № 4.1
2017 год

2. План

• 1. Теплопередача.
• 2. Передача теплоты через однослойную плоскую стенку
при граничных условиях III–го рода.
• 3. Передача теплоты через многослойную плоскую стенку
при граничных условиях III–го рода.
• 4. Передача теплоты через однослойную цилиндрическую
стенку при граничных условиях III–го рода.
• 5.
Передача
теплоты
через
многослойную
цилиндрическую стенку при граничных условиях III–го
рода.
• 6. Передача теплоты через шаровую стенку при
граничных условиях III–го рода.

3. 1. Теплопередача

Теплоотдачей называется процесс теплообмена между
поверхностью тела (или стенкой) и обтекающей эту
поверхность жидкой или газообразной средой.
Перенос теплоты от одной подвижной среды (горячей)
к другой (холодной) через однослойную или
многослойную твердую стенку любой формы
называется теплопередачей.

4. Примеры теплопередачи

Передача теплоты от горячей воды к воздуху
помещения через стенки нагревательных батарей
центрального отопления.
Передача теплоты от дымовых газов к воде через
стенки кипятильных туб в паровых котлах.
Передача теплоты от конденсирующего пара к воде
через стенки труб конденсатора.

5. Примеры теплопередачи

Передача теплоты от нагретых газов к воде через
стенку цилиндра двигателя внутреннего сгорания.
Во всех рассматриваемых случаях стенка служит
проводником теплоты и изготавливается из
материалов с высокой теплопроводностью.
Когда требуется уменьшить потери теплоты, стенка
должна быть изолятором и изготавливается из
материала
с
хорошими
теплоизоляционными
свойствами.

6.

• Стенки бывают самой разнообразной формы:
в виде плоских или ребристых листов;
в виде пучка цилиндрических, ребристых или
игольчатых труб;
в виде шаровых поверхностей и т. п.

7.

• Теплопередача – это очень сложный процесс,
в котором теплота передается всеми
способами:
теплопроводностью;
конвекцией;
излучением.

8.

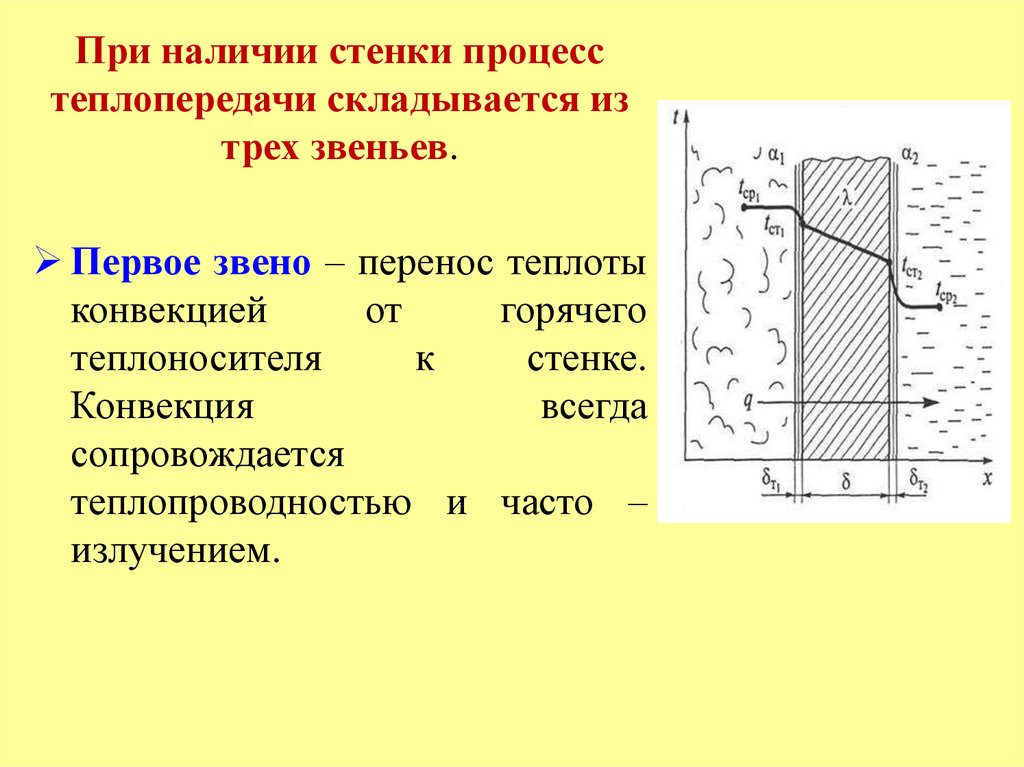
При наличии стенки процесс
теплопередачи складывается из
трех звеньев.
Первое звено – перенос теплоты
конвекцией
от
горячего
теплоносителя
к
стенке.
Конвекция
всегда
сопровождается
теплопроводностью и часто –
излучением.

9.

При наличии стенки процесс
теплопередачи складывается из
трех звеньев.
Второе звено – перенос теплоты
теплопроводностью через стенку.
При распространении теплоты в
пористых
телах
теплопроводность
связана
с
конвекцией и излучением в
порах.

10.

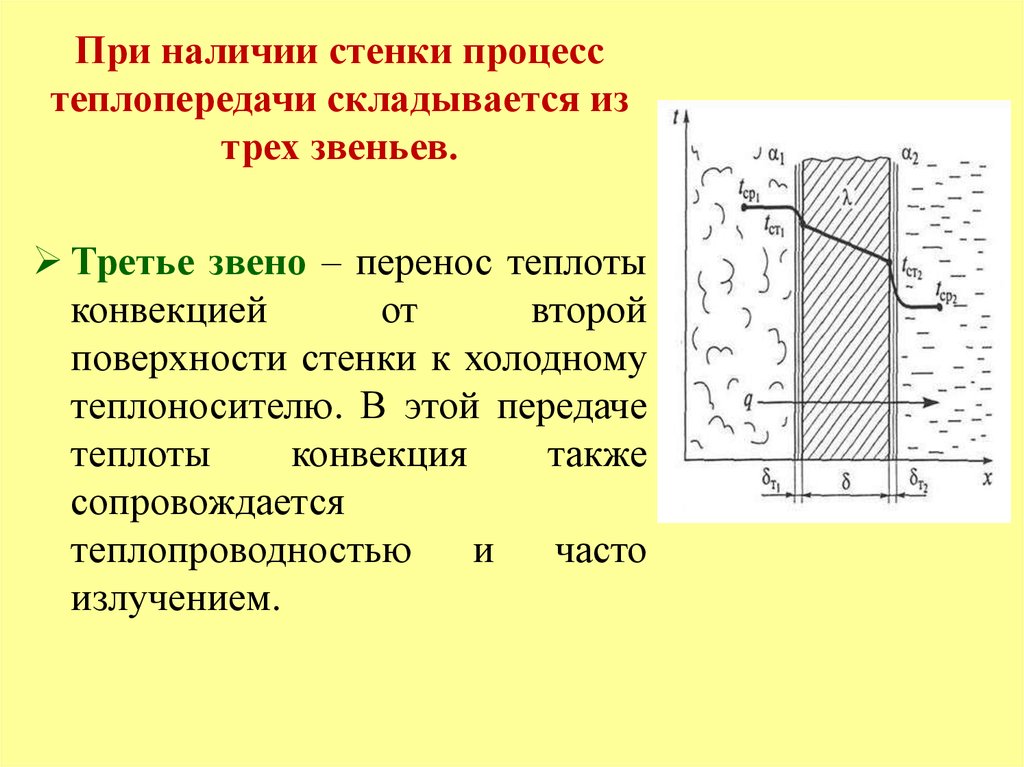
При наличии стенки процесс
теплопередачи складывается из
трех звеньев.
Третье звено – перенос теплоты
конвекцией
от
второй
поверхности стенки к холодному
теплоносителю. В этой передаче
теплоты
конвекция
также
сопровождается
теплопроводностью
и
часто
излучением.

11.

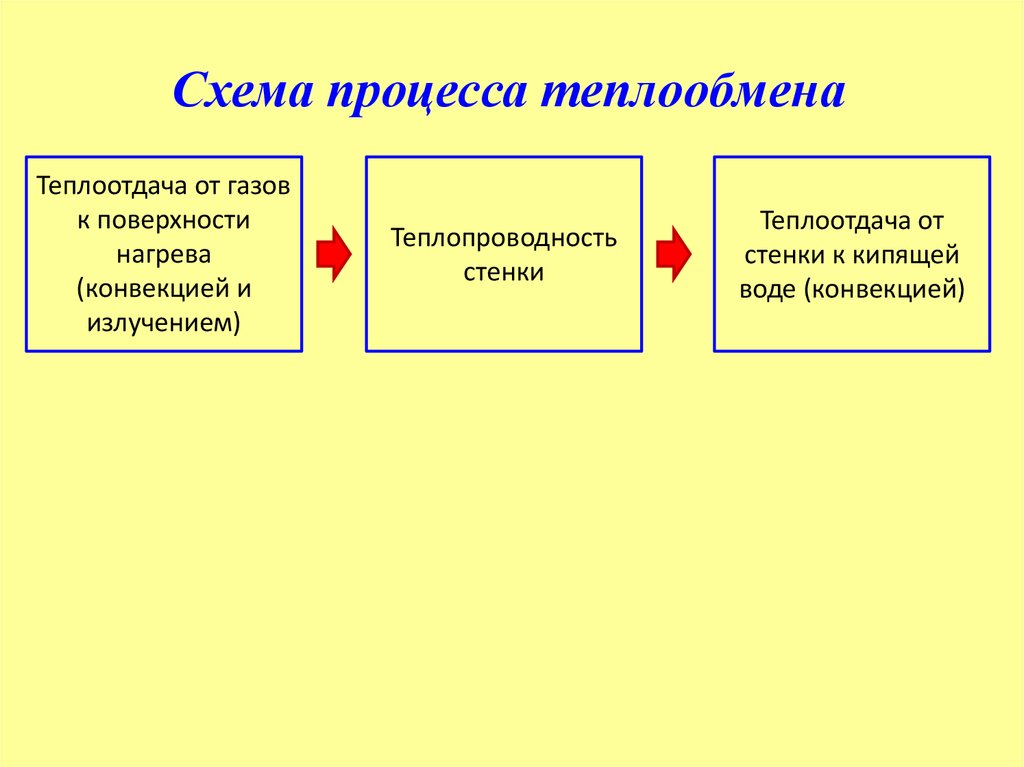
Схема процесса теплообмена
Теплоотдача от газов
к поверхности
нагрева
(конвекцией и
излучением)
Теплопроводность
стенки
Теплоотдача от
стенки к кипящей
воде (конвекцией)

12. 2. Передача теплоты через однослойную плоскую стенку при граничных условиях III–го рода

13.

Тепловой
поток,
переданной
горячим теплоносителем стенке
путем конвективного теплообмена,
определяется
по
уравнению
Ньютона – Рихмана:
Q 1F (tж1 tст1 ),
где α1 – коэффициент теплоотдачи от
горячего теплоносителя с постоянной
температурой tж1 к поверхности
стенки, учитывающий все виды
теплообмена;
F – площадь поверхности плоской
стенки.

14.

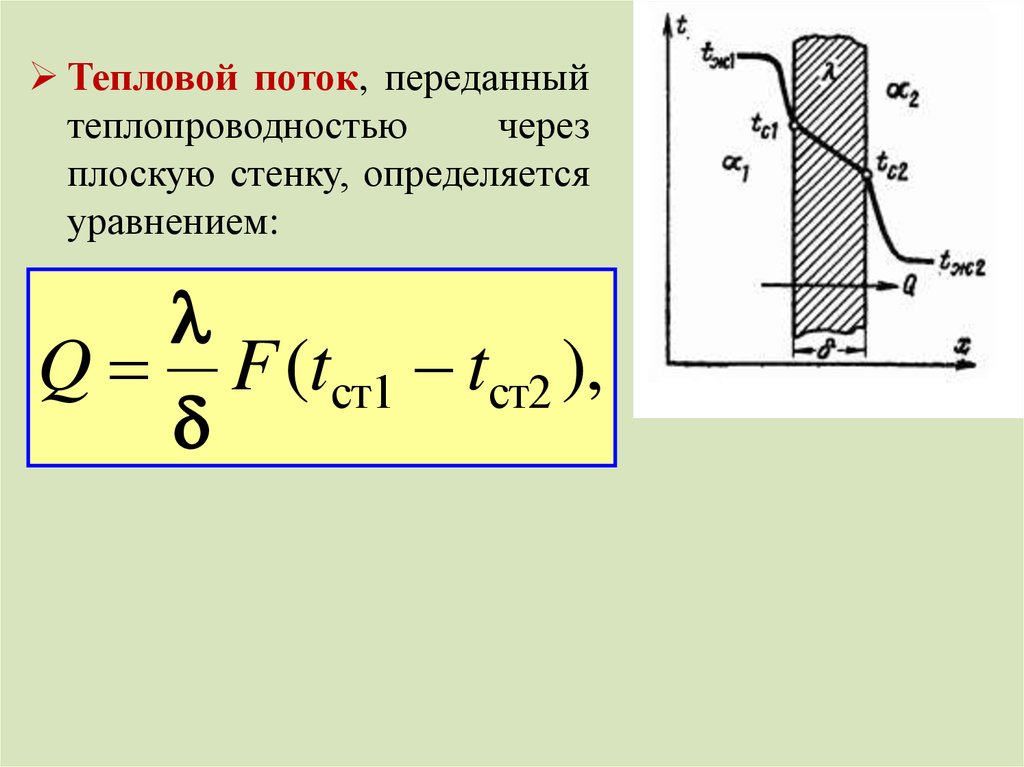
Тепловой поток, переданный
теплопроводностью
через
плоскую стенку, определяется
уравнением:
Q F (tст1 tст2 ),

15.

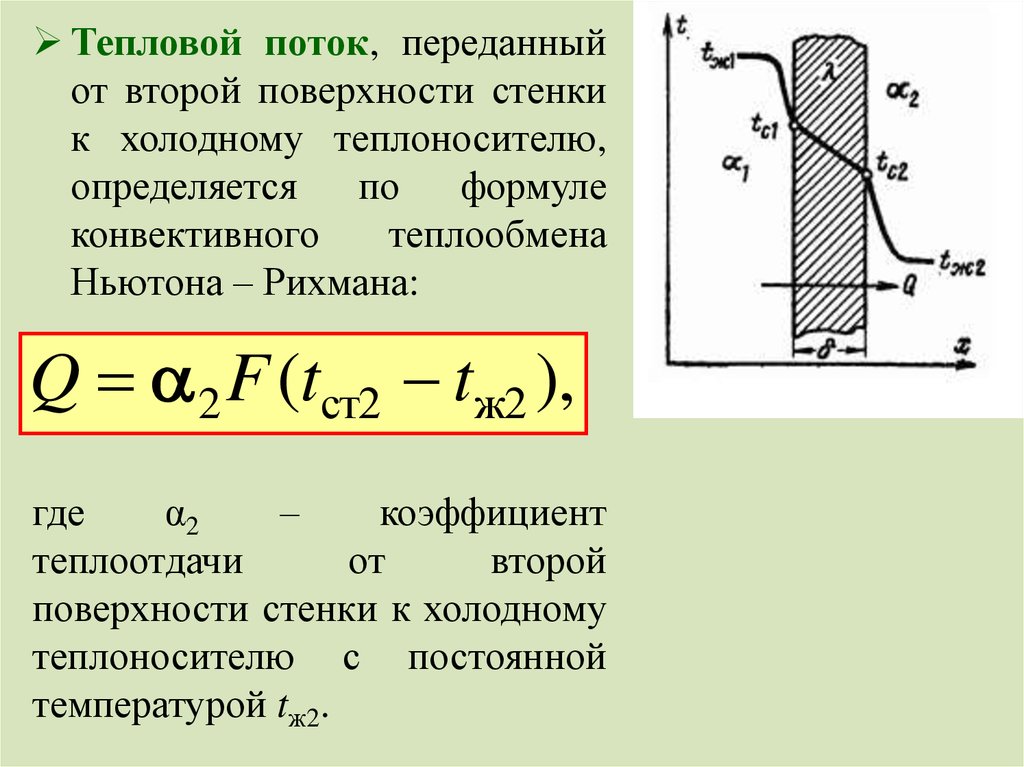
Тепловой поток, переданный
от второй поверхности стенки
к холодному теплоносителю,
определяется
по
формуле
конвективного
теплообмена
Ньютона – Рихмана:
Q 2 F (tст2 tж2 ),
где
α2
–
коэффициент
теплоотдачи
от
второй
поверхности стенки к холодному
теплоносителю с постоянной
температурой tж2.

16.

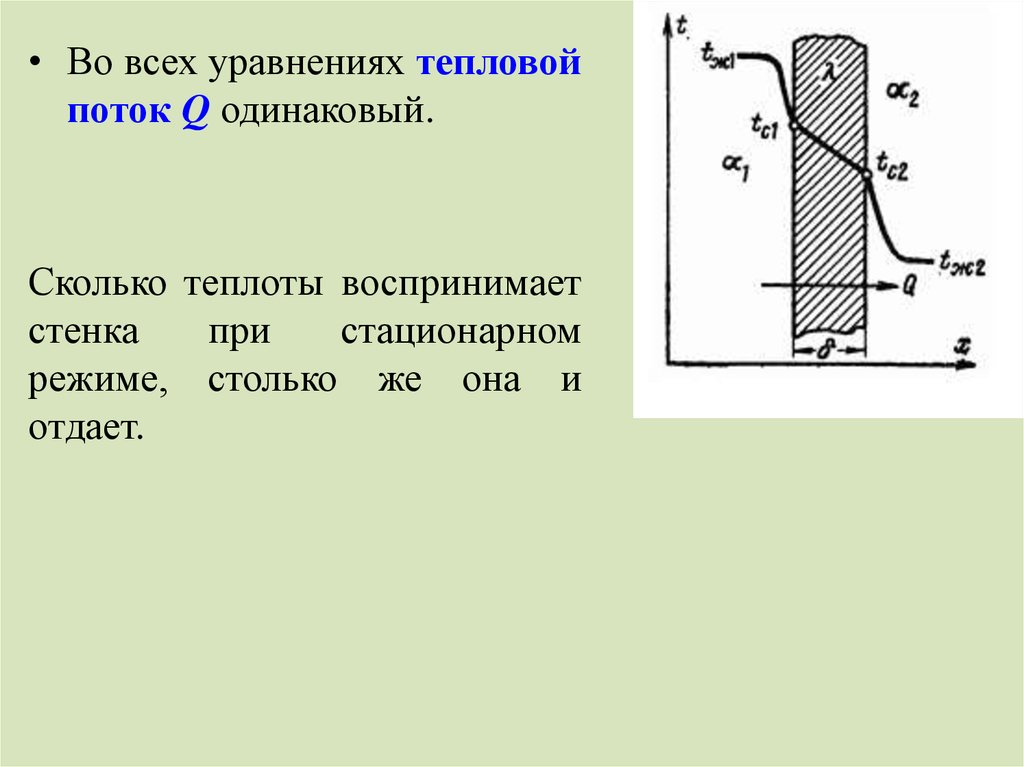
• Во всех уравнениях тепловой
поток Q одинаковый.
Сколько теплоты воспринимает
стенка
при
стационарном
режиме, столько же она и
отдает.

17. Коэффициент теплопередачи. Термическое сопротивление

18.

• Решая три уравнения переноса теплоты относительно
разности температур, имеем:
Q
t
t
,
ж1
ст1
1F
Q
tст1 tст2 ,
F
Q
t
t
.
ст2
ж2
F
2

19.

• Складывая полученные равенства, для теплового
потока получим
F t1 t2
Q
.
1 1
1 2

20.

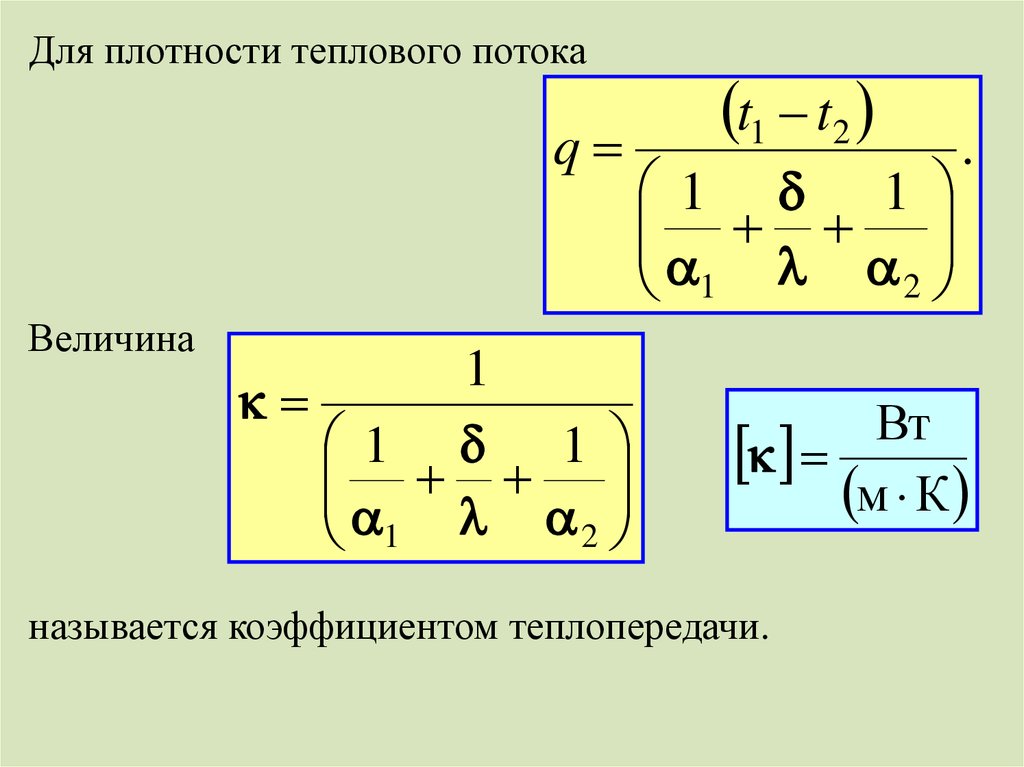
Для плотности теплового потока
q
Величина
1
1 1
1 2
t1 t2
1 1
1 2
.
Вт
м К
называется коэффициентом теплопередачи.

21.

Q F t1 t2 ,
q t1 t2 .
тепловой поток
Удельный тепловой поток
Вт
м К
Числовое значение коэффициента теплопередачи
выражает количество теплоты, проходящей через
единицу поверхности стенки в единицу времени от
горячего к холодному теплоносителю при разности
температур между ними в 1°.

22.

Уравнение
q t1 t2
называют уравнением теплопередачи.
• Для
определения
коэффициента
теплопередачи κ требуется предварительное
определение коэффициентов теплоотдачи α1
и α2, которые в большинстве случаев являются
величинами сложными.

23.

• Коэффициенты теплоотдачи учитывают передачи
теплоты конвекцией и излучением:
кон изл .
• Значение коэффициента теплопередачи κ всегда
меньше наименьшего коэффициента теплоотдачи
α.
• Величина, обратная коэффициенту теплопередачи
называется общим термическим сопротивлением R.

24.

• Общее
термическое
сопротивление
через
однослойную стенку определяется по формуле:
1 1 1
R .
1 2
1
1
и
1
2
м К
R 1
.
Вт
2
– внешние термические сопротивления.
– внутреннее термическое сопротивление стенки.

25. 3. Передача теплоты через многослойную плоскую стенку при граничных условиях III–го рода

26.

• В случае передачи теплоты через многослойную плоскую
стенку в знаменателе нужно учитывать сумму всех
термических сопротивлений слоев:
F tж1 tж 2
Q
,
1 i n i
1
1 i 1 i 2
Q
tж1 tж 2
q
.
F 1 i n i 1
1 i 1 i 2

27.

• Коэффициент теплопередачи через многослойную
плоскую стенку
1
.
1 i n i
1
1 i 1 i 2
• Общее
термическое
многослойную стенку
сопротивление
1 1
i
1
R
.
1 i 1 i 2
i n
через

28.

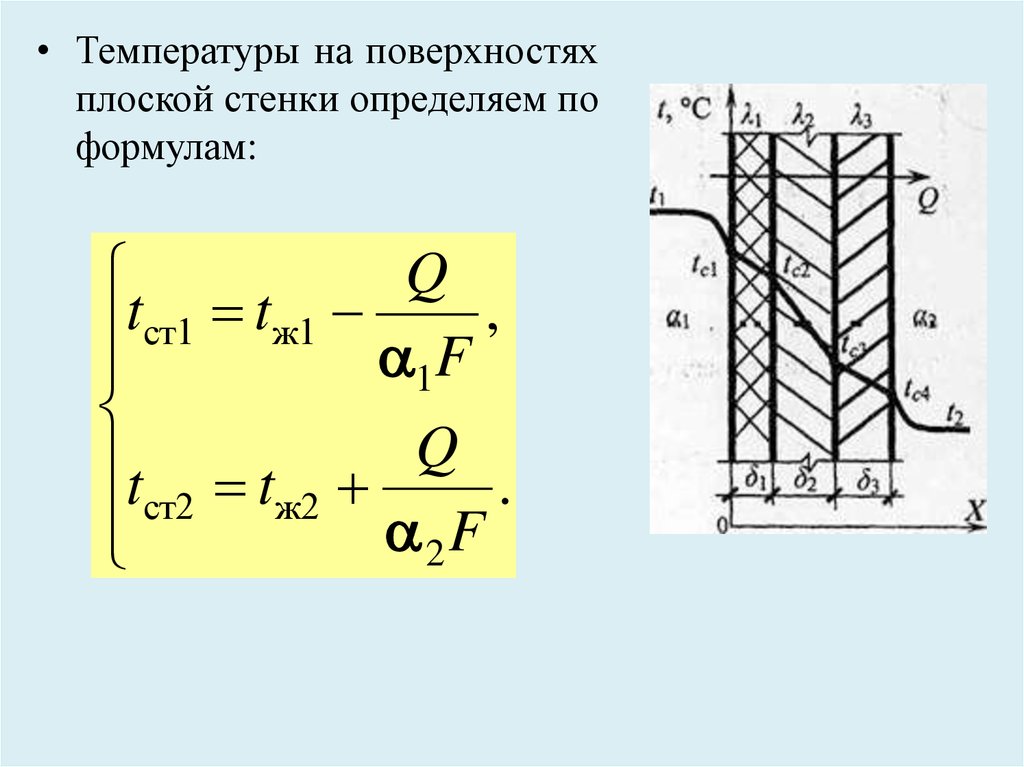
• Температуры на поверхностях
плоской стенки определяем по
формулам:
Q
t
t
,
ст1
ж1
1F
t t Q .
ст2
ж2
2 F

29.

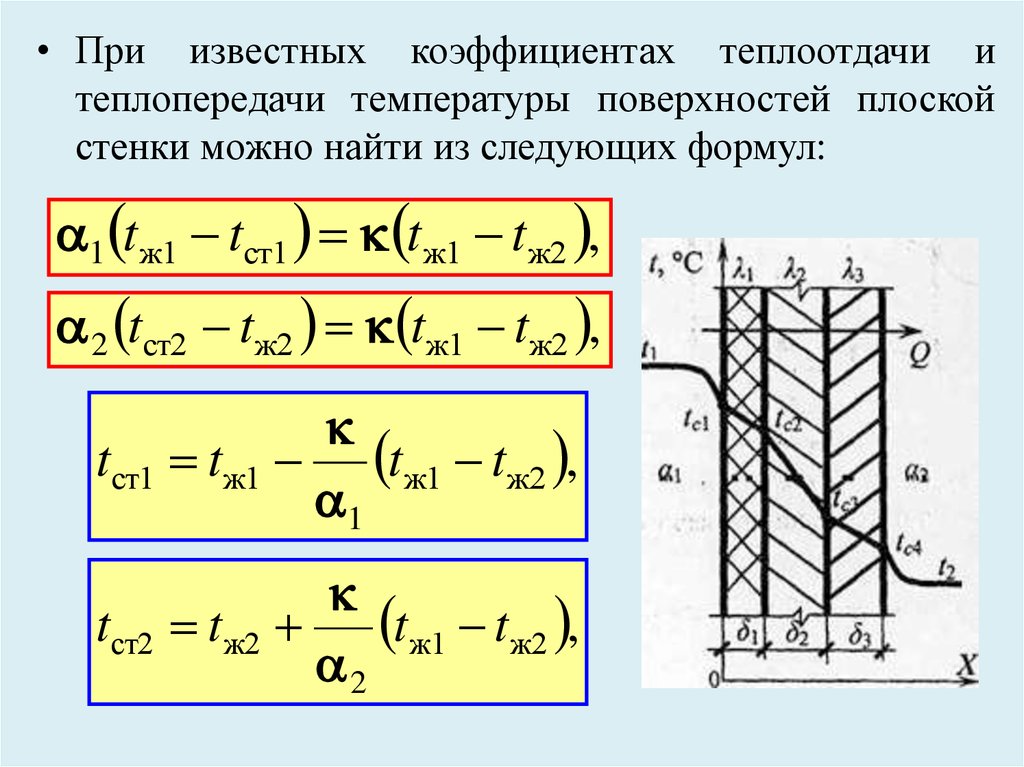
• При известных коэффициентах теплоотдачи и
теплопередачи температуры поверхностей плоской
стенки можно найти из следующих формул:
1 tж1 tст1 tж1 tж2 ,
2 tст2 tж2 tж1 tж2 ,
tст1 tж1 tж1 tж2 ,
1
tст2
tж1 tж2 ,
tж2
2

30. 4. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях III–го рода

Через
цилиндрическую
однородную
стенку
переносится теплота при стационарном режиме от
горячего теплоносителя с постоянной температурой tж1
и коэффициентом теплоотдачи α1 к холодному
теплоносителю с постоянной температурой tж2 и
коэффициентом теплоотдачи α2.

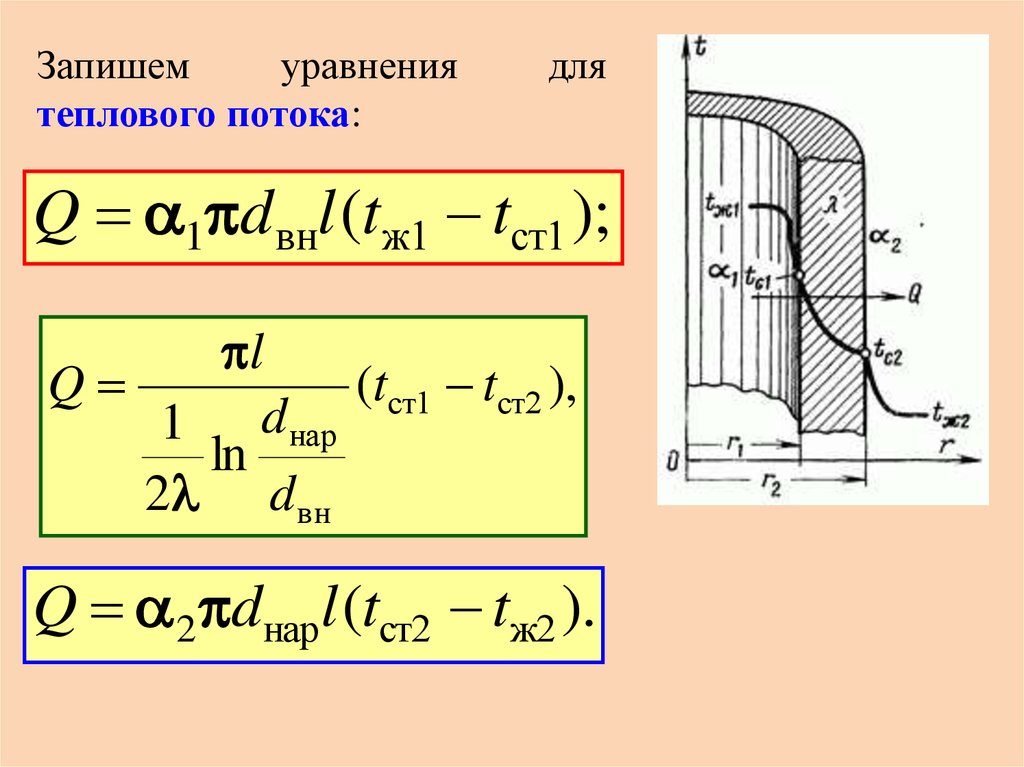
31.

Запишем
уравнения
теплового потока:
для
Q 1 dвнl (tж1 tст1 );
l
Q
(tст1 tст2 ),
1 d нар
ln
2 d вн
Q 2 dнар l (tст2 tж2 ).

32. Линейный коэффициент теплопередачи

Решая эти уравнения относительно
температур и складывая их, получим:
Q
1
d
1 вн
разности
l tж1 tж 2
,
1 d нар
1
ln
2 d вн 2 d нар

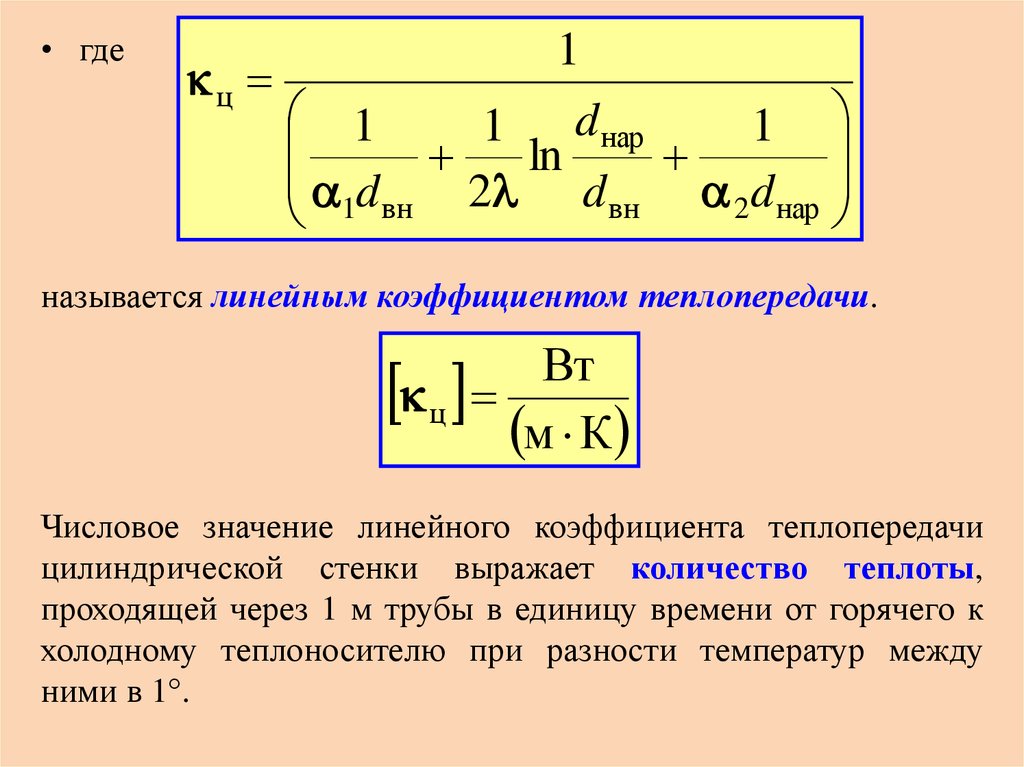
33.

• где
ц
1
d
1 вн
1
1 d нар
1
ln
2 d вн 2 d нар
называется линейным коэффициентом теплопередачи.
Вт
ц
м К
Числовое значение линейного коэффициента теплопередачи
цилиндрической стенки выражает количество теплоты,
проходящей через 1 м трубы в единицу времени от горячего к
холодному теплоносителю при разности температур между
ними в 1°.

34.

• Плотность теплового
проходящего
цилиндрическую стенку,
потока,
через
Q
qц ц tж1 tж 2 .
l
• Для теплового потока можно
записать уравнение в следующем
виде:
Q ц l tж1 tж 2 .

35. 5. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях III–го рода

36.

• Тепловой поток при переносе
теплоты через многослойную
цилиндрическую
стенку,
имеющую n слоев определяется
по формуле:
Q
l t1 t2
i n
1
1
d
1
i 1
ln
d
2
d
d
i
2 нар
1 вн i 1
.

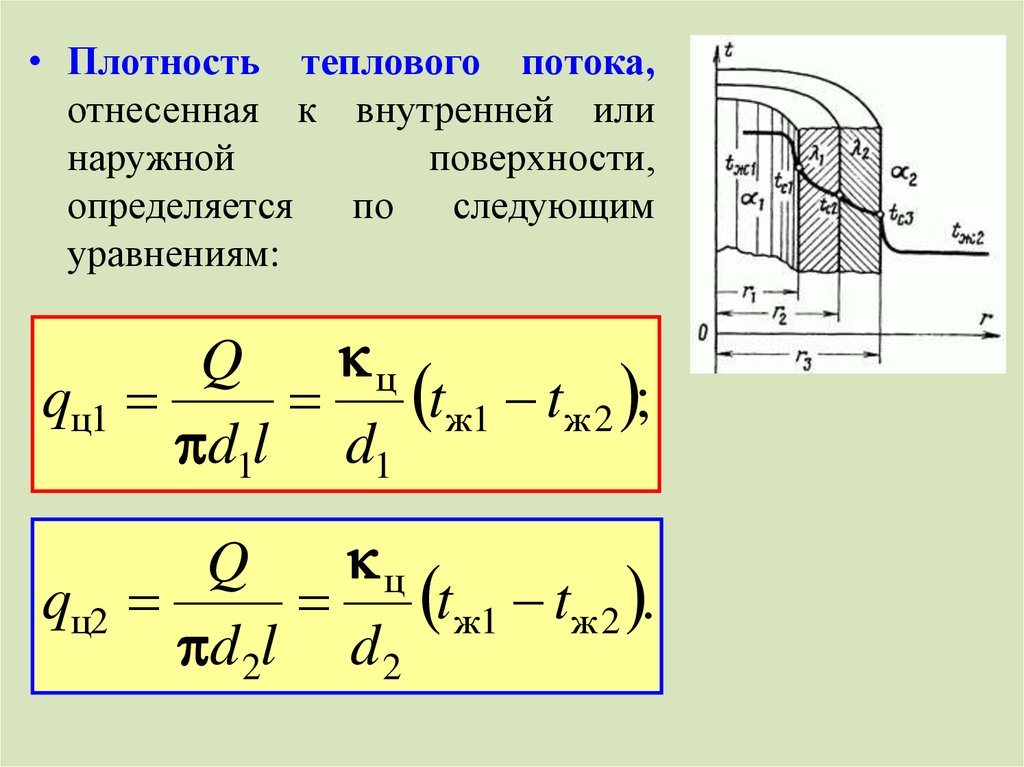
37.

• Плотность теплового потока,
отнесенная к внутренней или
наружной
поверхности,
определяется по следующим
уравнениям:
ц
Q
tж1 tж 2 ;
qц1
d1l d1
ц
Q
tж1 tж 2 .
qц2
d 2l d 2

38.

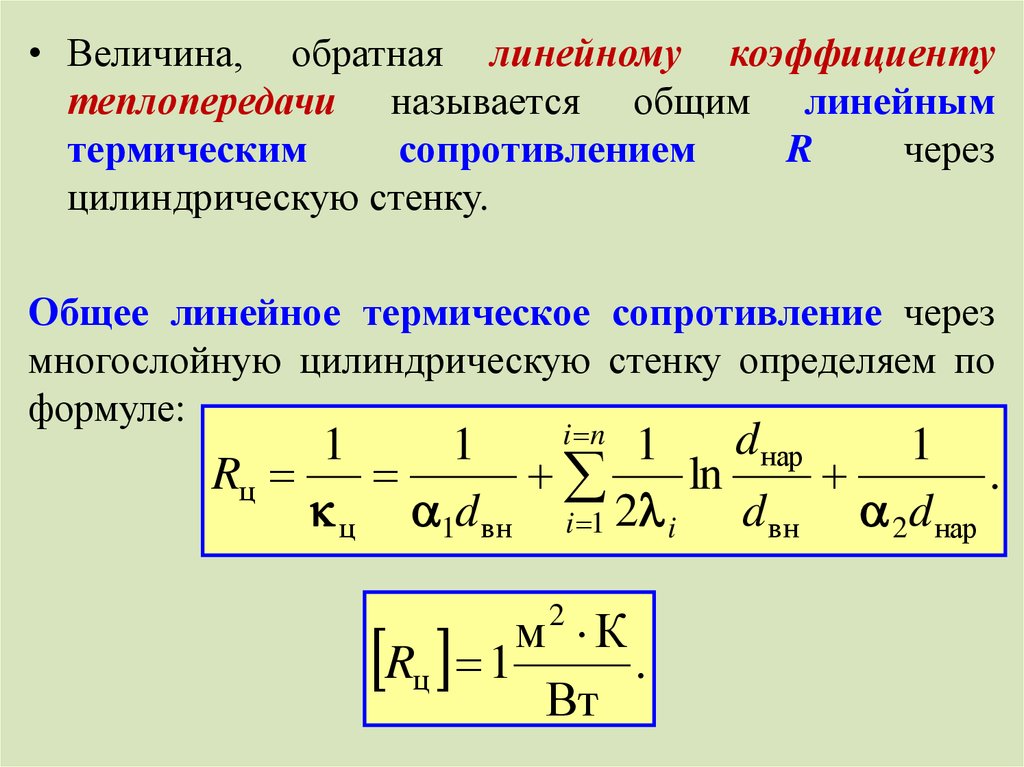
• Величина, обратная линейному коэффициенту
теплопередачи называется общим линейным
термическим
сопротивлением
R
через
цилиндрическую стенку.
Общее линейное термическое сопротивление через
многослойную цилиндрическую стенку определяем по
формуле:
i n 1
d нар
1
1
1
Rц
ln
.
ц 1dвн i 1 2 i d вн 2 d нар
м К
Rц 1
.
Вт
2

39.

1
1
и
– внешние термические
2dнар
1d вн
сопротивления.
i n
1
di 1
2 ln d
i 1
i
i
– внутреннее термическое
сопротивление стенки.

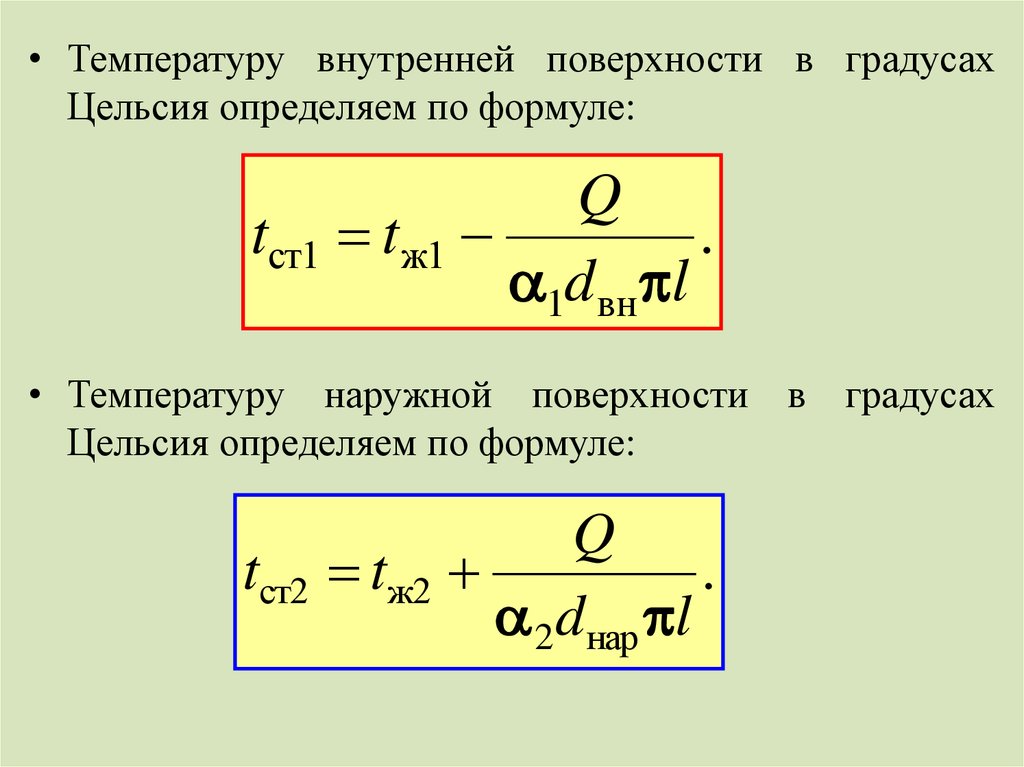
40.

• Температуру внутренней поверхности в градусах
Цельсия определяем по формуле:
Q
tст1 tж1
.
1dвн l
• Температуру наружной поверхности в градусах
Цельсия определяем по формуле:
tст2
Q
tж2
.
2dнар l

41. 6. Передача теплоты через шаровую стенку при граничных условиях III–го рода

42.

• При граничных условиях третьего рода для полого
шара известны:
внутренний d1 и внешний d2 диаметры;
температура горячего теплоносителя внутри шара t1 и
температура холодного теплоносителя t2;
коэффициент теплоотдачи от горячей жидкости к
внутренней поверхности шара α1 и коэффициент
теплоотдачи от наружной поверхности шара к
окружающей среде α2.

43.

• При стационарном режиме для всех изотермических
поверхностей тепловой поток постоянный:
Q
2
1 d1 (t1
tст1 );
2
Q
(tст1 tст2 ),
1 1
d1 d 2
Q
2
2 d 2 (tст2
t2 ).

44.

• Решая три уравнения относительно разности
температур и складывая их, находим тепловой поток:
t1 t2
Q
,
1
1 1 1
1
2
2
1d1 2 d1 d 2 2d 2
• или
Q ш t1 t2 .

45.

• Из уравнения для теплового потока определяем
коэффициент теплопередачи для шаровой стенки:
1
ш
1
1 1 1
1
2
2
1d1 2 d1 d 2 2 d 2
Вт
ш
К

46.

• Обратную величину коэффициенту теплопередачи
для шаровой стенки называют общим термическим
сопротивлением шаровой стенки.
1
1
1 1 1
1
Rш
.
2
2
ш 1d1 2 d1 d 2 2 d 2