Похожие презентации:
Теплопередача или теплообмен
1.
2.
• Теплопередача или теплообмен — учение осамопроизвольных необратимых процессах
распространения теплоты в пространстве.
• Тепловым потоком называется поток
внутренней энергии, самопроизвольно
возникающий в вещественной среде с
неоднородным температурным полем. В
простейшем случае, когда нет физикохимических превращений, взаимной
диффузии разнородных веществ, больших
скоростей течения и т. п., тепловой поток
направлен из области с более высокой
температурой в область с низкой
температурой.
3. Различают три процесса переноса теплоты:
•ТепловоеТеплопроводность
(кондукция)—процесс
излучение —
процесс распространения
распространения
энергии
только вследствие
теплоты
с
помощью
электромагнитных
волн,
взаимодействия структурных частиц вещества
обусловленный
только
температурой
оптическими
(молекул, ионов,
атомов,
свободныхиэлектронов),
свойствами
обусловленный
излучающего
переменностью
тела; притемпературы
этом внутренняя
в
рассматриваемом
В чистом виде
энергия
тела (среды)пространстве.
переходит в энергию
теплопроводность
имеет
место
в
твердых
телах
и
излучения.
Процесс
превращения
внутренней
неподвижных
слоях
жидкости и газа;
энергии
вещества
в
энергию
излучения,
переноса
• Конвекция (перемешивание) возможна только в
излучения
и его поглощения
веществом
называется
текучей среде
(жидкостях, газах,
сыпучих
средах,
теплообменом
плазме). Под излучением.
конвекцией теплоты понимают
процесстеплообменом
ее переноса приназываются
перемещении
объемов
Сложным
процессы
жидкости
или газа
в пространстве
из области с
переноса
теплоты
одновременно
несколькими
одной температурой в область с другой
способами—теплопроводностью,
конвекцией
температурой. При этом перенос
теплоты и
тепловым
неразрывно
излучением.
связан с переносом самой среды
4.
• Совместный процесс переноса теплоты конвекцией итеплопроводностью называется конвективным теплообменом.
• Процессы конвективного теплообмена всегда связаны с
теплопроводностью внутри перемещающихся значительных
(молярных) элементов потока вещества.
• Теплообмен, обусловленный совместным переносом теплоты
излучением и теплопроводностью, называют радиационнокондуктивным теплообменом.
• Если перенос теплоты осуществляется дополнительно и
конвекцией, то такой процесс называют радиационноконвективным теплообменом.
5.
• Теплоотдачей называется процесстеплообмена (теплопереноса) между
средами, разделенными отчетливой
границей (твердая стенка—текучая среда,
поверхность раздела газ — жидкость или
двух несмешивающихся жидкостей)
• Теплопередачей называется процесс
теплообмена между средами,
разделенными некоторой перегородкой.
6.
• Часто процессы переноса теплоты сопровождаются переносомвещества. Совместный молекулярный и конвективный перенос
массы называют конвективным массообменом. При наличии
массообмена процесс теплообмена усложняется. Теплота
дополнительно может переноситься вместе с массой
диффундирующих веществ.
• При теоретическом исследовании теплообмена считается, что
рассматриваемые газы, жидкости и твердые тела считаются
сплошной средой, т. е. средой, при рассмотрении которой допустимо
пренебречь ее дискретным строением.
• Различают однородные и неоднородные сплошные среды. В
однородных средах физические свойства в различных точках
одинаковы при одинаковых температуре и давлении, в
неоднородных средах различны.
• Различают изотропные и анизотропные сплошные среды. В любой
точке изотропной среды ее физические свойства не зависят от
выбранного направления,и наоборот, в анизотропной среде
некоторые свойства в данной точке могут быть функцией
направления.
• Сплошная среда может быть однофазной и многофазной. В
однофазной среде, состоящей из чистого вещества или из смеси
веществ, свойства изменяются в пространстве непрерывно. В
многофазной среде, состоящей из ряда однофазных частей, на
границах раздела свойства изменяются скачками.
7. Дифференциальное уравнение теплопроводности
Граничные условия8.
dQx q x dy dz d подведенноетепло
dQx dx q x dx dy dz d отведенное тепло
Разность между ними
dQx q x dy dz d q x dx dy dz d
Z
dQz+dz
Разложивполученную функцию в ряд Тейлора получим
dQy
q xdV в
dQx1
dx
dy dz d
d
x
Аналогично можно найти все остальные подведенные теплоты
dQх
q x q y q z
dx dy dz d
dQ1
y
z
x
dQ2 q vdv d
dQх+dx
dQy+dy
dz
dQ находим в зависимости dQz
от характера термодинам
.процесса
Так при изохорном процессе dQ dU
dx
dt
dU c v Y d dv
d
dy
X
9. Подставив все полученные выражения, получим дифференциальное уравнение энергии для изохорного процесса переноса теплоты
q x q y q zt
q v
cv
y
z
x
Получим дифференциальное уравнение энергии для
изобарного процесса переноса теплоты
dQ1 dQ2 dH
h
dH d dv
q x q y q z
h
q v
y
z
x
10. В твердых телах перенос теплоты осуществляется по закону Фурье
q x t / xq y t / y
q z t / z
Разность
примем
между с v c p c мала
с без индекса
Дифференциальное уравнение
теплопроводности
t
1 t t t q v
c x x y y z z c
11. Если принять теплофизические характеристики постоянными, то уравнение примет вид
t2 t 2 t 2 t q v
2
2
2
c x
y
z c
2
2
2
t
t
t
2
a; 2 2 2
c
y
z
x
t
qv
2
Получим a t
c
12.
• Коэффициент пропорциональности a, м2/с, называетсякоэффициентом температуропроводности и является
физическим параметром вещества.
• Он существен для нестационарных тепловых процессов и
характеризует скорость изменения температуры.
• Коэффициент температуропроводности является мерой
теплоинерционных свойств тела.
• Изменение температуры во времени dtld для любой точки
пространства пропорционально величине а. Скорость
изменения температуры в любой точке тела будет тем
больше, чем больше коэффициент
температуропроводности а.
• При прочих равных условиях выравнивание температур во
всех точках пространства будет происходить быстрее в
том теле, которое обладает большим коэффициентом
температуропроводности.
• Коэффициент а зависит от природы вещества. Жидкости и
газы обладают малым коэффициентом
температуропроводности. Металлы обладают малой
тепловой инерционностью и имеют большой коэффициент
температуропроводности.
13. Если система тел не содержит внутренних источников теплоты (qv = 0),то диф.уравнение теплопроводности получит вид уравнения Фурье
При стационарной теплопроводности иЕсли система тел не содержит внутренних
отсутствии внутренних источников теплоты
источников теплоты (qv = 0),то диф.уравнение
диф.уравнение принимает вид уравнения
теплопроводности получит вид уравнения
Лапласса
Фурье
t 2 2
a t
t t t
0
x 2 y 2 z 2
2
2
Если система тел имеет внутренние источники теплоты
но температурное поле соответствует стационарному
состоянию, т. е. t = t (х, у, z), то диф. уравнение
теплопроводности превращается в уравнение Пуассона
t t t qv
0
x 2 y 2 z 2
2
2
2
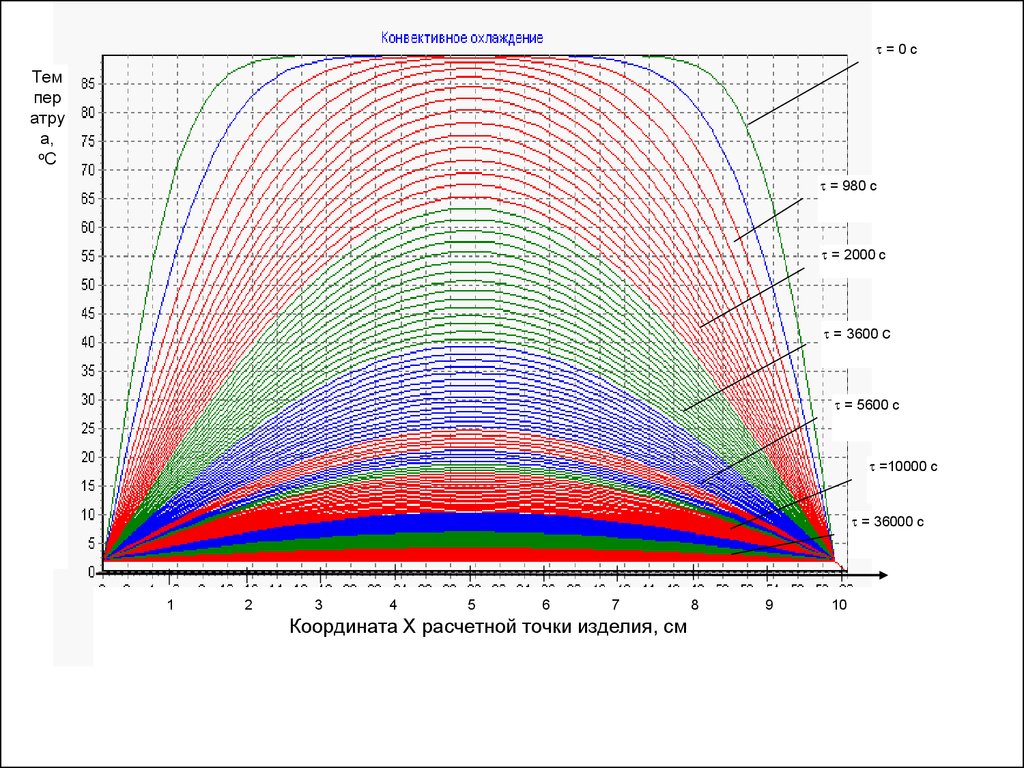
14.
=0сТем
пер
атру
а,
оС
= 980 с
= 2000 с
= 3600 с
= 5600 с
=10000 с
= 36000 с
1
2
3
4
5
6
7
Координата Х расчетной точки изделия, см
8
9
10
15. УСЛОВИЯ ОДНОЗНАЧНОСТИ
• Чтобы выделить конкретно рассматриваемый процесс и дать егополное математическое описание, к диф.уравнению необходимо
присоединить математическое описание всех частных особенностей
рассматриваемого процесса. Эти частные особенности называются
условиями однозначности или краевыми условиями.
• Условия однозначности включают в себя:
• геометрические условия, характеризующие форму и размеры тела, в
которых протекает процесс; они определяют форму и линейные
размеры тела.
• физические условия, характеризующие физические свойства среды и
тела; задаются физическими параметрами тела и может быть задан,
закон распределения внутренних источников теплоты.
• временные (начальные) условия, характеризующие распределение
температур в изучаемом теле в начальный момент времени;
необходимы при рассмотрении нестационарных процессов и состоят в
задании закона распределения температуры внутри тела в начальный
момент времени. Начальное условие аналитически может быть
записано при = 0
t = f(x, у, z). При равномерном распределении
температуры в теле начальное условие упрощается (при = 0) t= to =
const.
• граничные условия, характеризующие взаимодействие
рассматриваемого тела с окружающей средой. Граничные условия
могут быть заданы несколькими способами
16. Граничные условия
• Граничные условия первого рода.Задается распределение температуры на поверхности тела для
каждого момента времени: tz = f(x, у, z, ),
где tz — температура на поверхности тела; х, у, z — координаты
поверхности тела.
• Граничные условия второго рода.
Задаются значения теплового потока для каждой точки поверхности
тела и любого момента времени : qp=f(x,y,z, )
• где— qp плотность теплового потока на поверхности тела; х, у, z —
координаты на поверхности тела.
• Граничные условия третьего рода.
• Задаются температура окружающей среды tc и закон теплообмена
между поверхностью тела и окружающей средой в процессе
охлаждения или нагревания тела.
• Для описания процесса теплообмена между поверхностью тела и
средой используется закон Ньютона—Рихмана- количество теплоты,
отдаваемое единицей поверхности тела в единицу времени,
пропорционально разности температур поверхности тела tz и
окружающей среды tc
• q= (tc-tz)
17.
где — коэффициент пропорциональности, называемыйкоэффициентом теплоотдачи, Вт/(м2-К), характеризует
интенсивность теплообмена между поверхностью тела и
окружающей средой. Численно он равен количеству
теплоты, отдаваемому (или воспринимаемому) единицей
поверхности в единицу времени при разности температур
между поверхностью тела и окружающей средой, равной
одному градусу.
18.
• Согласно закону сохранения энергииколичество теплоты, которое отводится
с единицы поверхности в единицу
времени вследствие теплоотдачи,
должно равняться количеству теплоты,
подводимому к единице поверхности в
единицу времени вследствие
теплопроводности из внутренних
объемов тела, т. е.
где n — нормаль к
поверхности тела;
индекс „с" указывает на то,
что температура и градиент
относятся к поверхности
тела (при n = 0).
19.
• Дифференциальное уравнениеt
qv
2
a t
c
с заданными условиями однозначности дает
полную математическую формулировку
краевой задачи теплопроводности.
Поставленная таким образом задача
разрешается аналитическим, численным или
экспериментальным методом.
20. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
• Пристационарном
тепловом
режиме
температура
тела во времени
остается
постоянной, т. е.
dt/d = 0.
qv
a t
0
c
qv
2
t
0
2
или
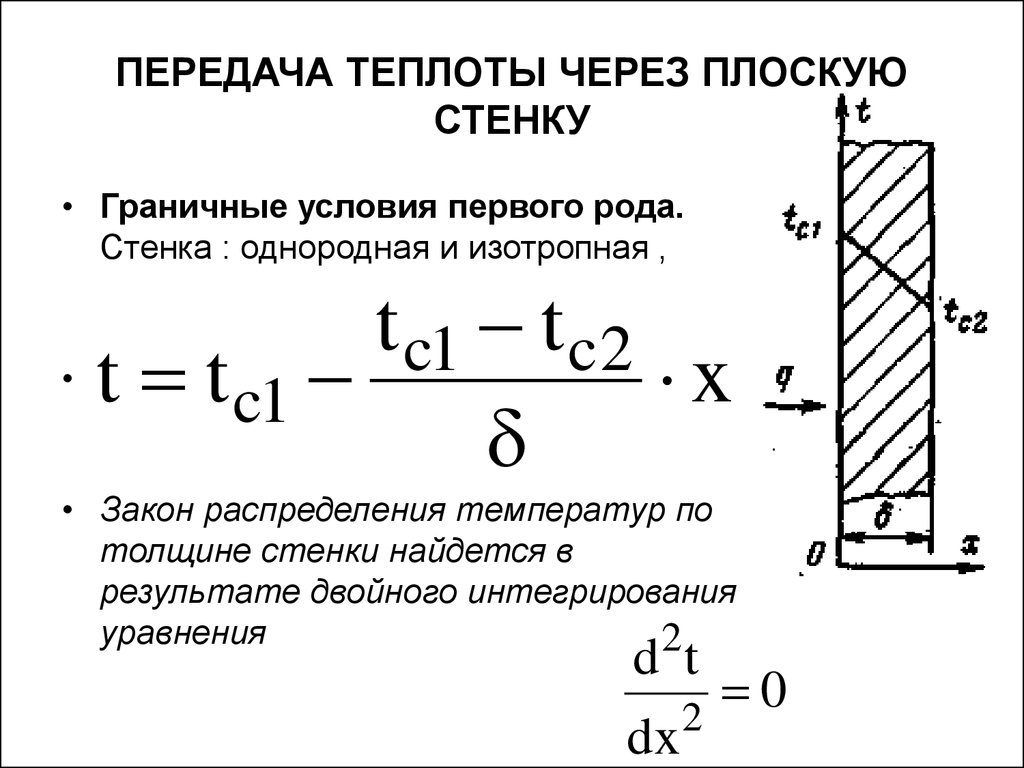
21. ПЕРЕДАЧА ТЕПЛОТЫ ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ
• Граничные условия первого рода.Стенка : однородная и изотропная ,
толщина с постоянным коэффициентом
теплопроводности .
• На наружных поверхностях стенки
поддерживают постоянными
температуры tс1 и tc2.
• Закон распределения температур по
толщине стенки найдется в
результате двойного интегрирования
уравнения
2
t c1 t c 2
t t c1
x
d t
dx
2
0
22. Граничные условия второго рода:
• ГраничныеКоличество
теплоты,
через
условия
второгопроходящее
рода:
единицу поверхности стенки в единицу времени,
Для определения количества теплоты, проходящего
прямо
пропорционально коэффициенту
через единицу поверхности стенки в единицу времени в
теплопроводности
температур
направлении оси ,
Ох,разности
воспользуемся
закономна
Фурье,
наружных
поверхностях стенки и обратно
согласно которому
пропорционально толщине стенки.
Тепловой поток определяется не
абсолютным
получим
значением температур, а их разностью которую
принято называть температурным напором.
Отношение / (Вт/(м2-К)), называется
c
1
c
2
тепловой проводимостью стенки, а обратная
величина подставив
/ (м2· К/Вт) — тепловым или
термическим, сопротивлением стенки и
представляетcсобой
падение
температуры в стенке
1
c
2
на единицу плотности теплового потока.
t
q
x
t
( t t ) /
x
q (t t )
23. Общее количество теплоты
Q q F ( t c1 t c 2 )F (Дж)Где q – плотность теплового потока, Вт/м2;
F – площадь теплопередающей поверхности, м2;
- время воздействия теплового потока, с.
t c1 t c 2
t c1 t c 2 q
x
подставив в выражение t t c1
Получим
q
t t c1 x
При прочих равных условиях
температура в стенке убывает
тем быстрее, чем больше
плотность теплового потока
24.
• Если коэффициент теплопроводностизависит от температуры, то q можно
вычислять в предположении, что = const,
принимая для него среднее значение в
интервале температур от tcl до tc2.
• Это же определение относится ко всем
теплофизическим значениям параметров
системы.
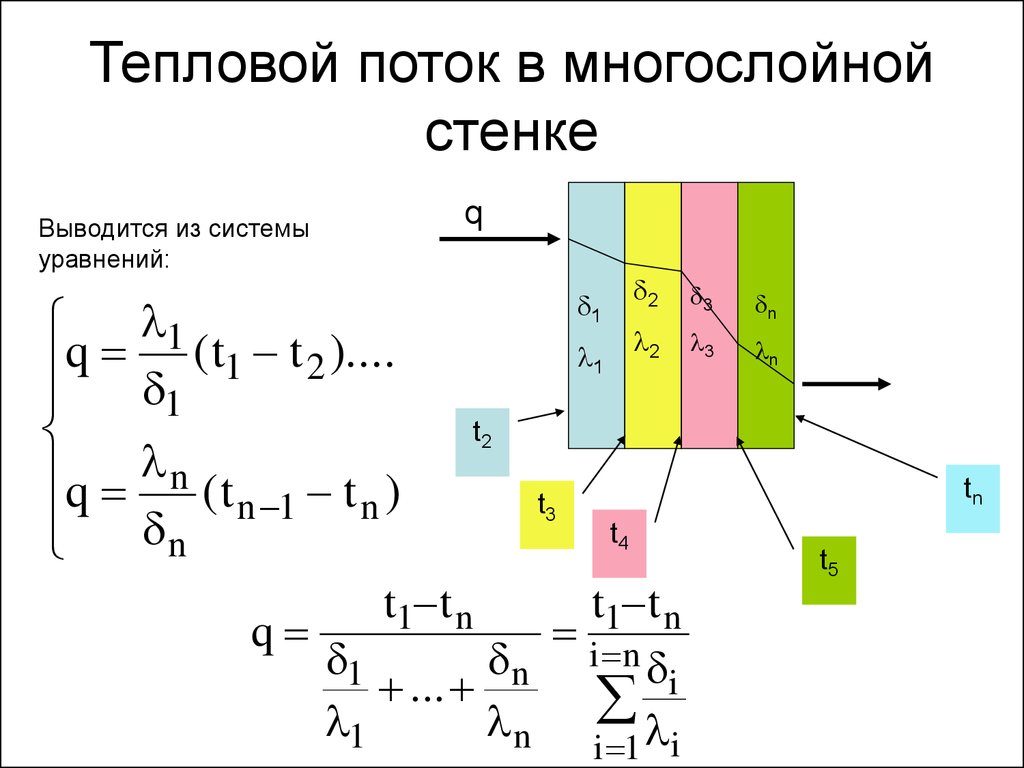
25. Тепловой поток в многослойной стенке
qВыводится из системы
уравнений:
1
q
(
t
t
)....
1
2
1
q n ( t
n 1 t n )
n
1
1
2
3
2
n
3
n
t2
t1 t n
t3
tn
t4
t1 t n
q
i n
1
n
i
...
1
n i
i 1
t5
26.
Внутри каждого изслоев температура
изменяется
прямолинейно , а
для многослойной
стенки в целом
температурная
кривая
представляет
ломаную линию
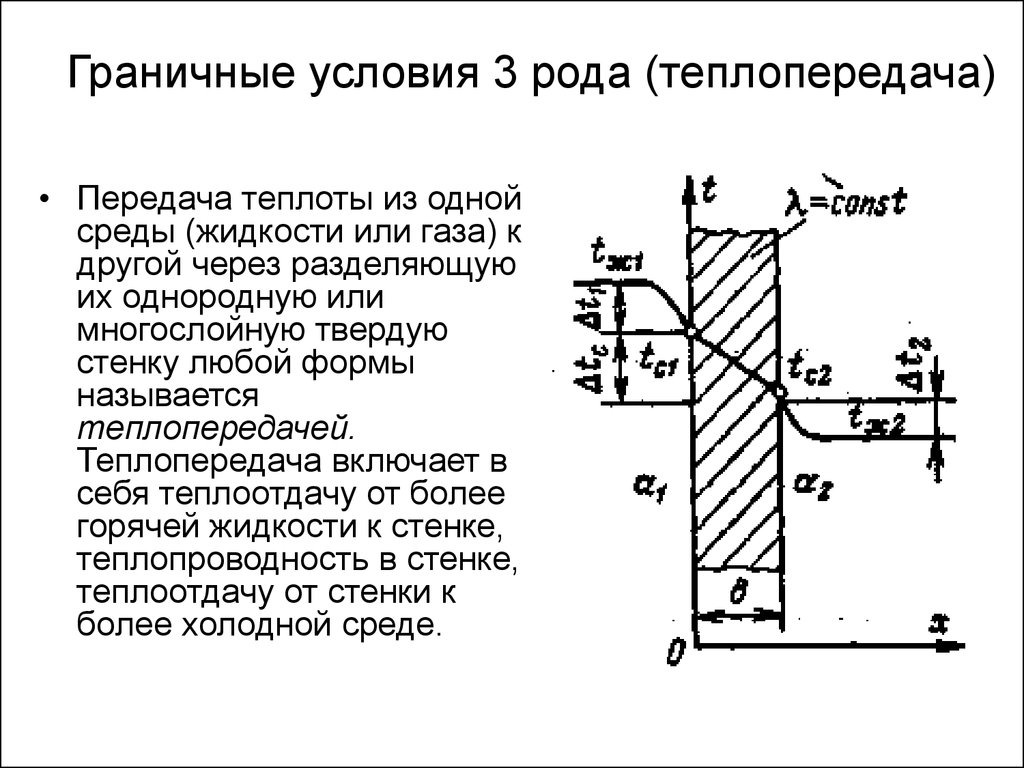
27. Граничные условия 3 рода (теплопередача)
• Передача теплоты из однойсреды (жидкости или газа) к
другой через разделяющую
их однородную или
многослойную твердую
стенку любой формы
называется
теплопередачей.
Теплопередача включает в
себя теплоотдачу от более
горячей жидкости к стенке,
теплопроводность в стенке,
теплоотдачу от стенки к
более холодной среде.
28. Выводим уравнение теплопередачи
q 1( t ж1 t c1)q ( t c1 t c 2 )
q 2 (t c2 t ж 2 )
Получим
1 1
q( ) t ж1 t ж 2
1 2
Если
1
k
1 1
(
)
1 2
1
q ( t ж1 t c1)
1
q ( t c1 t c 2 )
1
q
(t c2 t ж 2 )
2
С
л
о
ж
и
т
ь
t ж1 t ж 2
q
1 1
( )
1 2
q k ( t ж1 t ж 2 )
29.
• Величина k имеет ту же размерность, что и ,и называется коэффициетом теплопередачи.
• Коэффициент теплопередачи k характеризует
интенсивность передачи теплоты от одной
жидкости к другой через разделяющую их
стенку и численно равен количеству теплоты,
которое передается через единицу
поверхности стенки в единицу времени при
разности температур между жидкостями в
один градус.
• Величина, обратная коэффициенту
теплопередачи, называется полным
термическим сопротивлением
теплопередачи
1 1
R
1 2
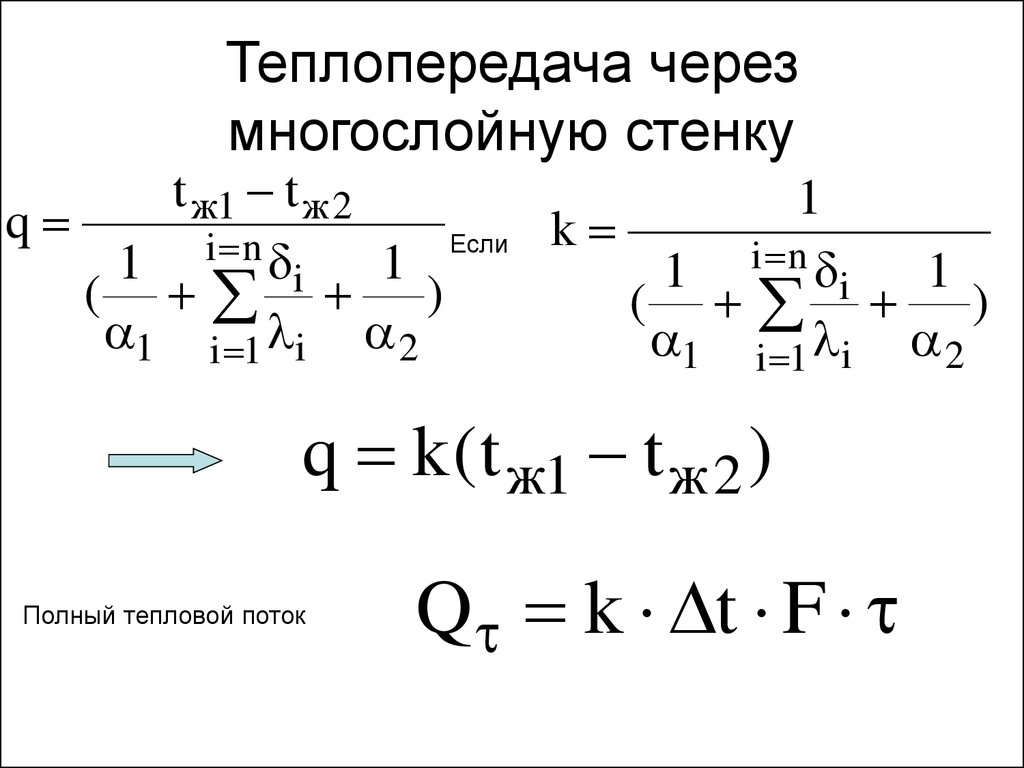
30. Теплопередача через многослойную стенку
t ж1 t ж 21
q
k
Если
i
n
i n
1
i
1
1
1
i
( )
( )
1 i 1 i 2
1 i 1 i 2
q k ( t ж1 t ж 2 )
Полный тепловой поток
Q k t F
31.
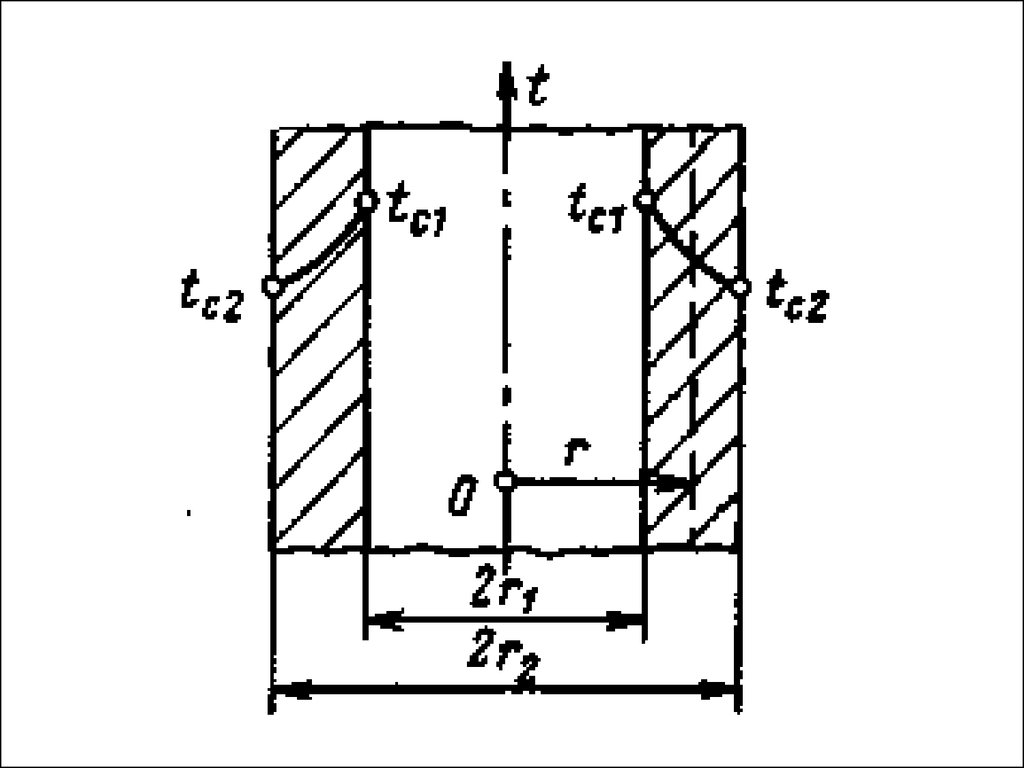
32. Теплопередача через цилиндрическую стенку
Полный тепловой потоктолько через стенку
Линейная
плотность
теплового потока
через
стенку(отнесенна
я к единице
длины трубы)
Линейные плотности
теплового потока при
теплопередаче
2 ( t c1 t c2 )
Q
d2
ln
2 ( t c1 t c2 )
d1
q
d2
d1 ln
d1
q 1 d1( t ж1 t c1)
( t c1 t c 2 )
q
1 d2
ln
2 d1
q 2 d 2 ( t c 2 t ж 2 )
33.
k1
1
1 d2
1
(
ln
)
1d1 2 d1 2d 2
q k ( t ж1 t ж 2 )
34. Многослойная цилиндрическая стенка
• при =const. Используяпринцип сложения
сопротивлений, получим
выражение для теплового
потока Q через многослойную
цилиндрическую стенку .
• где - теплопроводность i-го
слоя; Т - полный перепад
температур на внутренней и
внешней поверхностях
многослойной цилиндрической
стенки; Ri, Ri+1 - внутренний,
наружный радиусы i-гo слоя.
2 T
Q n
1
R i 1
ln R
i
1
w1
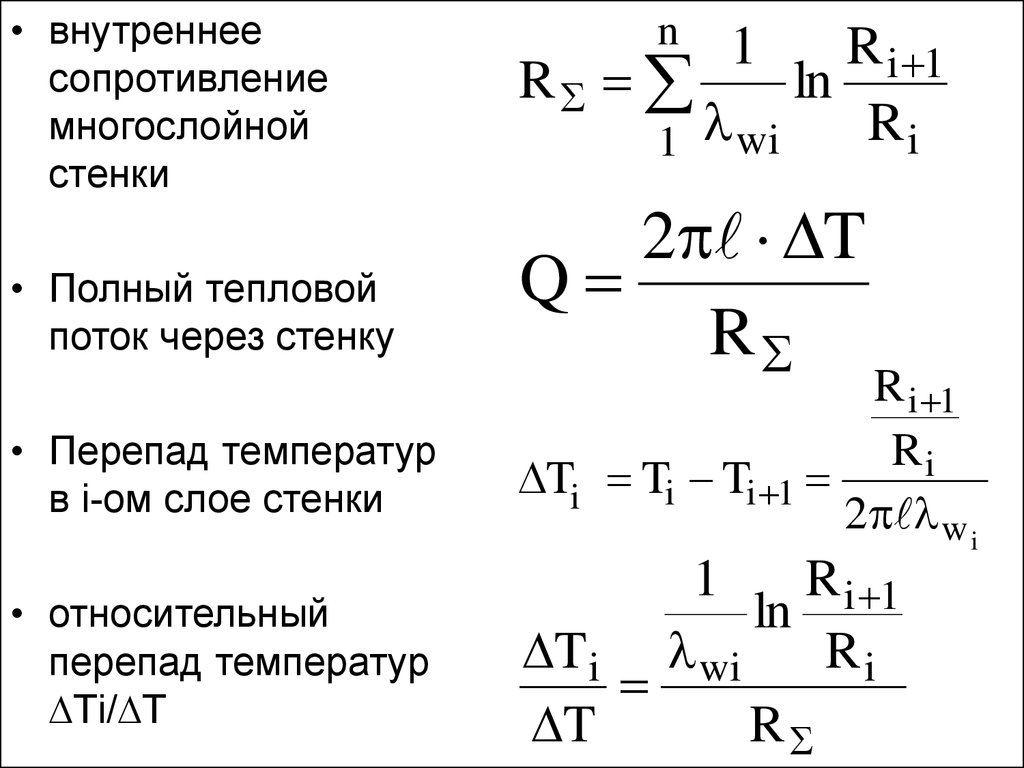
35.
• внутреннеесопротивление
многослойной
стенки
• Полный тепловой
поток через стенку
n
1
R i 1
R
ln
Ri
1 wi
2 T
Q
R
• Перепад температур
в i-ом слое стенки
R i 1
Ri
Ti Ti Ti 1
2 w i
• относительный
перепад температур
Тi/ Т
1
R i 1
ln
Ti wi
Ri
T
R
36.
• Общее термическое сопротивлениемногослойной цилиндрической стенки
R
n 1
1
R i 1
1
ln
1R1 1 wi
Ri
2R n 1
• Полный тепловой поток через многослойную
цилиндрическую стенку
Q
2 (Tw1 Tw 2 )
R
37. КРИТИЧЕСКИЙ ДИАМЕТР ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
• Общее термическое сопротивлениецилиндрической стенки
1
1 d2
1
*
R
ln
1d1 2 d1 2 d 2
• зависит от внешнего диаметра трубы R2
неоднозначно.
• Исследуя величину R* на экстремум в
зависимости от R2 (npи прочих постоянных
величинах), получим
38.
• Экстремальное значение имеет место призначении d2=dкр которое найдем из условия
2 w
1
1
1
1
0
d кр
w 2R 2
w 2 R кр
2
• Значение dkp может соответствовать min или
max величины R в зависимости от знака 2-ой
производной
39.
• Подставляя R2=Rкр найдем знаквеличины в скобках
• Так как вторая производная больше
нуля, то значение dкр соответствует
минимуму термического сопротивления
и, соответственно максимуму тепловой
проводимости и теплового потока.
40.
• Критическийдиаметр
не потока
зависит
от
Зависимость
теплового
от
внешнего диаметра цилиндрической
размеров цилиндрической
трубы (R1,
стенки
R2), а определяется теплопроводностью
материала трубы ( w) и условиями
теплообмена на ее внешней
поверхности ( 2).
• В зависимости от соотношения dкр и d2
тепловой поток может соответствовать
максимально возможному (d2=dкр),
увеличиваться с ростом d2 (d2<dкр),
уменьшаться с ростом d2 (d2>dkp)
41. Критическая толщина изоляции
• Полученные соотношения позволяютвыбрать оптимальную толщину
изоляции и проанализировать влияние
ее параметров на величину теплового
потока. Если на внешней поверхности
трубы имеется изоляция толщиной из и
теплопроводностью из, то можно
записать соотношение
42.
• Условие «хорошей» изоляции• Изоляция считается эффективной, если
термическое сопротивление
изолированной трубы больше, чем
неизолированной
43.
• Диаметр эффективной изоляции dизопределим по соотношению
• Тепловой поток от неизолированной
внешней поверхности трубы
• Тепловой поток от изолированной
поверхности с толщиной изолированной
44.
• Их отношения равны• Выбрав какой-либо теплоизоляционный материал для
покрытия цилиндрической поверхности, прежде всего
нужно рассчитать критический диаметр для заданных из и
2.
• Если окажется, что значение dKp больше наружного
диаметра трубы d2, то применение выбранного материала в
качестве тепловой изоляции нецелесообразно. В области d2
< d3 < dKp. при увеличении толщины изоляции будет
наблюдаться увеличение теплопотерь.
• Только при d3 = d3 Эф тепловые потери вновь станут такими
же, как для первоначального, неизолированного
трубопровода. Следовательно, некоторый слой тепловой
изоляции не будет оправдывать своего назначения.
• Значит, для эффективной работы тепловой изоляции
необходимо, чтобы dкр.изоляции<d2
45.
46.
d кр2 w
2


























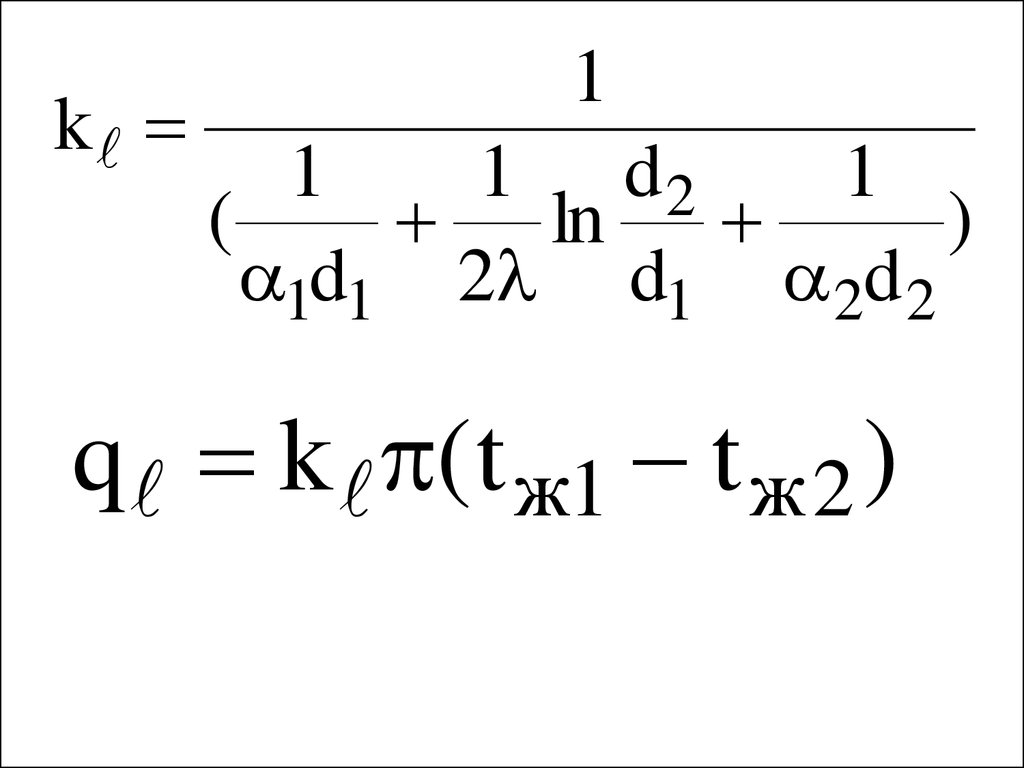













 Физика
Физика








