Игры с природой. Принятие решений в условиях неопределенности и риска

1. Игры с природой

Принятие решений в условиях неопределенности и риска

2. Теория принятия решений

• Теория принятия решений — аналитический подход к выбору
наилучшего действия (альтернативы) или последовательности
действий

3. Модели теории принятия решений

• выбор решений в условиях определенности, если относительно
каждого действия известно, что оно неизменно приводит к
некоторому конкретному исходу;
• выбор решения при риске, если каждое действие приводит к одному
из множества возможных частных исходов, причем каждый исход
имеет вычисляемую или экспертно оцениваемую вероятность
появления. Предполагается, что ЛПР эти вероятности известны или их
можно определить путем экспертных оценок;
• выбор решений при неопределенности, когда то или иное действие
или несколько действий имеют своим следствием множество частных
исходов, но их вероятности совершенно не известны или не имеют
смысла

4. Понятие риска

• Под риском принято понимать вероятность (угрозу) потери лицом
или организацией части своих ресурсов, недополучения доходов
или появления дополнительных расходов в результате
осуществления определенной производственной и финансовой
политики

5. Виды рисков

• производственный, связанный с возможностью невыполнения фирмой своих
обязательств перед заказчиком;
• кредитный, обусловленный возможностью невыполнения фирмой своих
финансовых обязательств перед инвестором;
• процентный, возникающий вследствие непредвиденного изменения
процентных ставок;
• риск ликвидности, обусловленный неожиданным изменением кредитных и
депозитных потоков;
• инвестиционный, вызванный возможным обесцениванием инвестиционнофинансового портфеля, состоящего из собственных и приобретенных ценных
бумаг;
• рыночный, связанный с вероятным колебанием рыночных процентных ставок
как собственной национальной денежной единицы, так и зарубежных курсов
валют

6. Динамический и статический риски

• Динамический риск связан с возникновением непредвиденных
изменений стоимости основного капитала вследствие принятия
управленческих решений, а также рыночных или политических
обстоятельств. Такие изменения могут привести как к потерям,
так и к дополнительным доходам.
• Статический риск обусловлен возможностью потерь реальных
активов вследствие нанесения ущерба собственности и потерь
дохода из-за недееспособности организации

7. Основное назначение анализа риска

• Обеспечение партнеров информацией, необходимой для принятия решений о целесообразности участия в некотором проекте, и
предусмотрение мер по защите от возможных финансовых
потерь

8. Условия или предположения при анализе риска

• потери от риска не зависят друг от друга;
• потери по одному из некоторого перечня рисков не обязательно
увеличивают вероятность потерь по другим;
• максимально возможный ущерб не должен превышать
финансовых возможностей участников проекта

9. Факторы, влияющие на рост степени риска в проекте

• Объективные факторы непосредственно не зависят от самой
фирмы: это инфляция, конкуренция, анархия, политические и
экономические кризисы, экология, налоги и т.д.
• Субъективные факторы непосредственно характеризуют данную
фирму: это производственный потенциал, техническое оснащение,
уровень производительности труда, проводимая финансовая,
техническая и производственная политика, в частности выбор типа
контракта между инвестором и заказчиком.

10. Мера риска

• Мерой риска некоторого коммерческого (финансового) решения
или операции следует считать среднее квадратичное отклонение
(положительный квадратный корень из дисперсии) значения
показателя эффективности этого решения или операции.
• Показателем эффективности финансового решения (операции)
служит прибыль

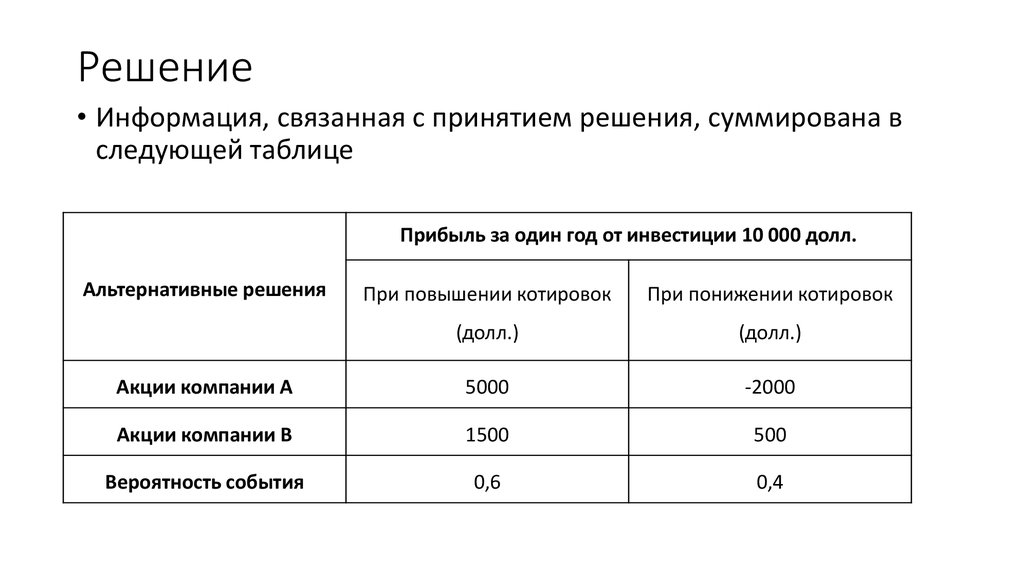
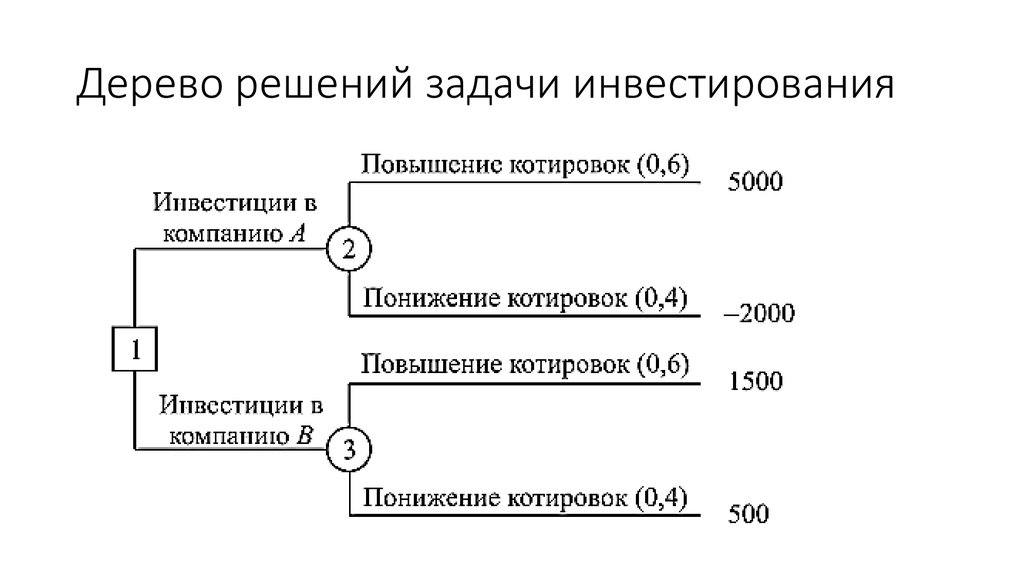
11. Пример

• Рассмотрим выбор некоторым лицом одного из двух вариантов
инвестиций в условиях риска. Пусть имеются два проекта А и В, в
которые указанное лицо может вложить средства. Проект А в
определенный момент в будущем обеспечивает случайную величину
прибыли. Предположим, что ее среднее ожидаемое значение,
2
m
математическое ожидание, равно A с дисперсией S A
• Для проекта В эти числовые характеристики прибыли как случайной
величины предполагаются равными соответственно mB и S B2
• Средние квадратичные отклонения равны соответственно S A и S B

12. Возможные случаи выбора проекта

a) тA = mB, SA < SB, следует выбрать проект А;
b) тA > mB, SA < SB, следует выбрать проект А;
c) тA > mB, SA = SB, следует выбрать проект А;
d) тA > mB, SA > SB;
e) тA < mB, SA < SB.
• В последних двух случаях решение о выборе проекта А или В
зависит от отношения к риску ЛПР

13. Пример выбора из более чем двух вариантов инвестиций

• Характеристики вариантов показаны точками
на плоскости (т, S), где т – средняя прибыль,
получаемая в результате инвестиции, а S –
среднее квадратичное отклонение прибыли
• Среди вариантов А, В и С наиболее
предпочтителен А.
• Из вариантов В, D и Н следовало бы выбрать
Н.
• Вариант Н лучше вариантов С и F.
• Сравнительная предпочтительность вариантов
А, D, F и G зависит от склонности ЛПР к риску

14. Неопределенность

• Лицу, принимающему решение известен лишь набор возможных
вариантов состояний внешней среды
• В условиях неопределенности вероятностное распределение,
соответствующее состояниям j ( j = 1, 2, ..., n) либо неизвестно,
либо не может быть определено
• Ситуация с полной неопределенностью характеризуется
отсутствием какой бы то ни было дополнительной информации

15. Матрица последствий

• Если будет принято i-e решение, а состояние внешней среды
соответствует j-й ситуации, то лицо, принимающее решение,
получит доход qij.
• Плата (или доход), связанная с решением Аi и состоянием
внешней среды sj, равна qij
• Матрица Q=(qij), i=1,2,…,m, j=1,2,…,n называется матрицей
последствий (платежной матрицей)

16. Матрица сожалений (рисков)

• Допустим, мы хотим оценить риск, который несет i-e решение. Нам
неизвестна реальная ситуация. Но если бы мы знали, что
осуществляется j-е состояние внешней среды, то выбрали бы
наилучшее решение, т. е. приносящее наибольший доход
qj = max(qkj), k=1,2,…,m
• Значит, принимая i-e решение, мы рискуем получить не qj, а только qij,
т. е. если мы примем i-е решение, а во внешней среде реализуется j-е
состояние, то мы будем сожалеть о недополученном доходе в размере
rij = qj – qij = max(qkj) – qij , k=1,2,…,m
• Матрица R= (rij ) называется матрицей сожалений (матрицей рисков)

17. Критерий Лапласа (критерий безразличия)

• Критерий Лапласа опирается на принцип недостаточного
основания, который гласит, что, поскольку распределение
вероятностей состояний Р(sj) неизвестно, нет причин считать
их различными. Следовательно, используется оптимистическое
предположение, что вероятности всех состояний природы равны
между собой, т.е.
P{s1} = P{s2} = ... = P{sn} = 1/n.
• Если при этом qij представляет получаемую прибыль, то
наилучшим решением является то, которое обеспечивает
max
1