Параллельность прямых в пространстве

1.

Параллельность
прямых в
пространстве.

2. Аксиомы группы С1

Какова бы ни была плоскость, существуют
точки, принадлежащие этой плоскости, и
точки, не принадлежащие ей.
А, С α
D
С
А
D, B, K α
К
B

3. Аксиомы группы С2

Если две различные плоскости имеют общую
точку, то они пересекаются по прямой,
проходящей через эту точку.
С
с

4. Аксиомы группы С3

Если две различные прямые имеют общую
точку, то через них можно провести
плоскость, и притом только одну.
С
a
b

5.

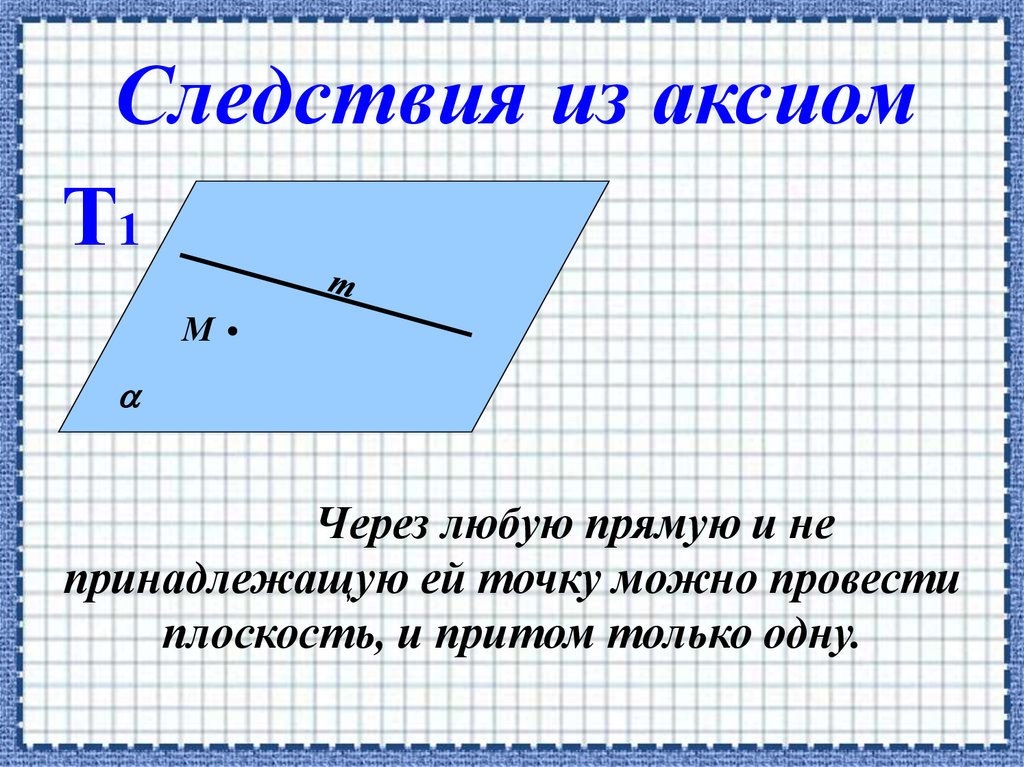
Следствия из аксиом
Т1
М
Через любую прямую и не
принадлежащую ей точку можно провести
плоскость, и притом только одну.

6.

Следствия из аксиом:
Т2
В
А
Если две точки прямой принадлежат
плоскости, то вся прямая принадлежит
плоскости

7.

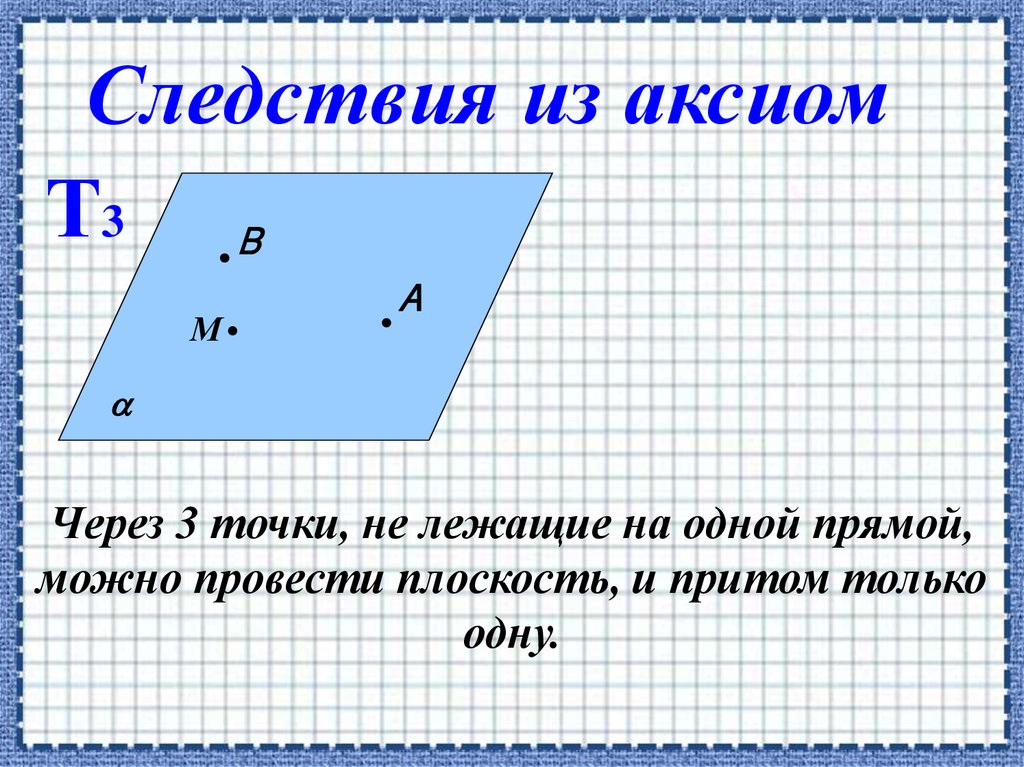
Следствия из аксиом
Т3 В
М
А
Через 3 точки, не лежащие на одной прямой,
можно провести плоскость, и притом только
одну.

8.

Следствие из Т
1
Через две ПАРАЛЛЕЛЬНЫЕ прямые
проходит плоскость, и притом только одна.

9.

Вывод
Как в пространстве можно однозначно
задать плоскость?
Способы задания плоскостей
1. По трем точкам
2. По прямой и не принадлежащей ей
точке.
3. По двум пересекающимся прямым.
4. По двум параллельным прямым.
Рисунок

10.

Решение задач
В
•С
Дано: АВСDпараллелограмм
А, В, С α
Доказать: D α
(самостоятельно)
А
А, В АВ, С,D СD,
•D
Доказательство:
АВ СD (по определению параллелограмма) АВ, СD α D α

11.

12.

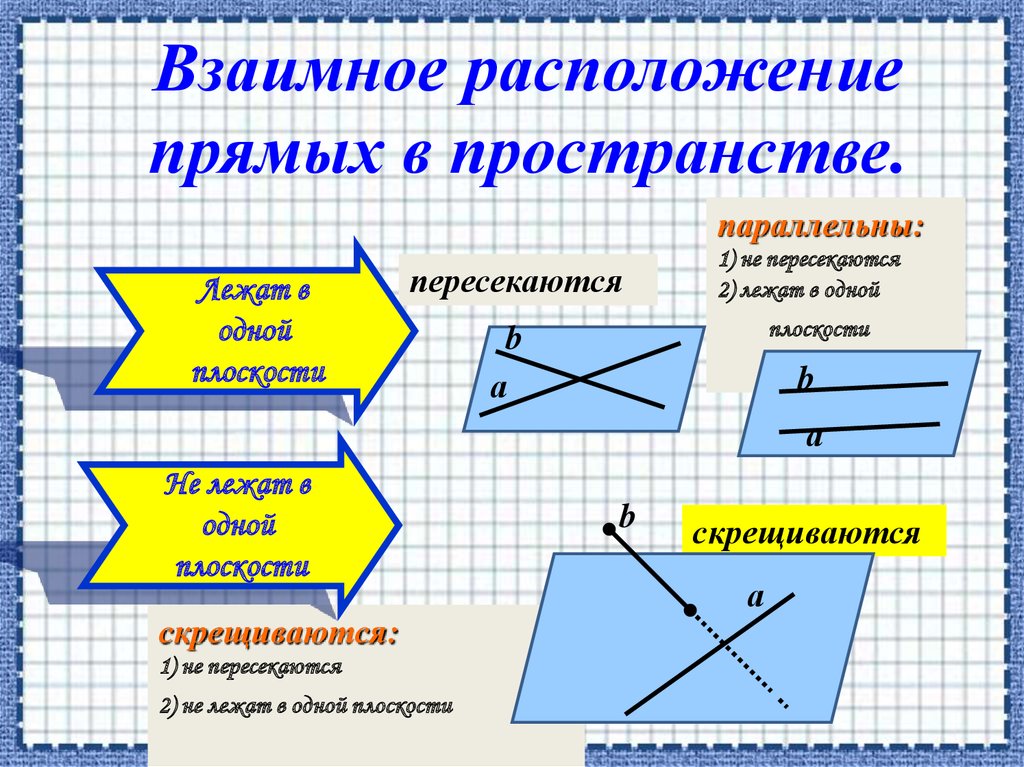
Взаимное расположение
прямых в пространстве.
параллельны:
Лежат в
одной
плоскости
пересекаются
1) не пересекаются
2) лежат в одной
плоскости
b
а
b
а
Не лежат в
одной
плоскости
скрещиваются:
1) не пересекаются
2) не лежат в одной плоскости
b
скрещиваются
а

13.

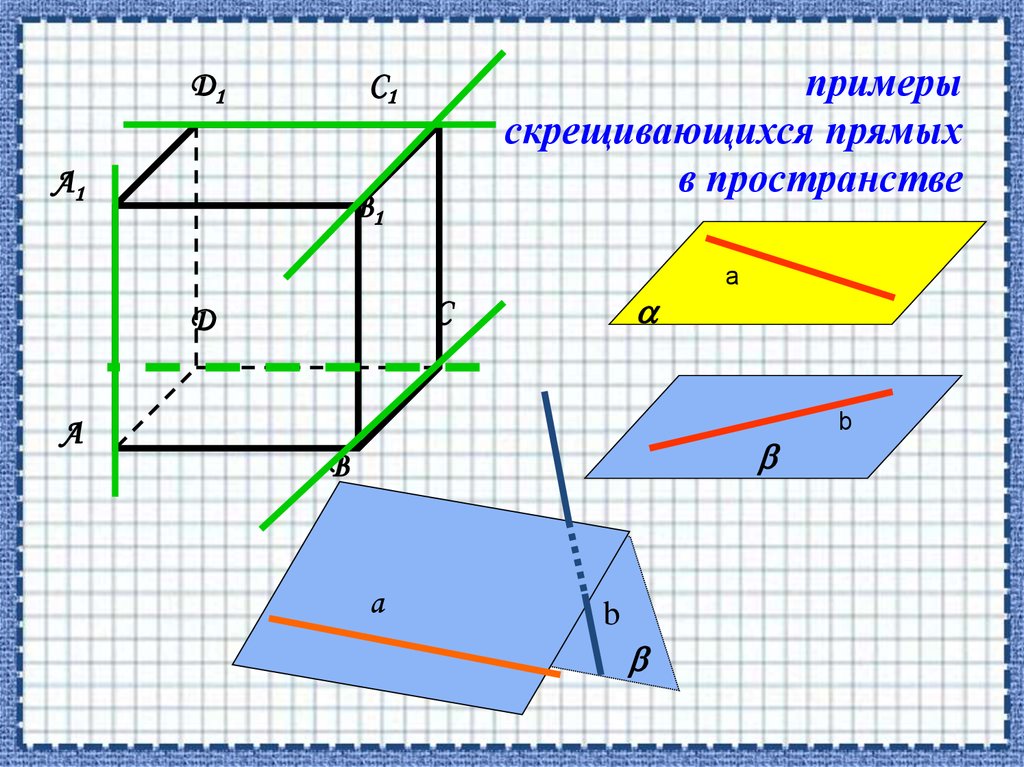
Д1
примеры
скрещивающихся прямых
в пространстве
С1
А1
В1
С
Д
А
В
а
а
b
b

14.

15.

16.

17.

18.

Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка
проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите
длину отрезка ВВ1, если
1) СС1=15 см, АС:ВС=2:3,
2) СС1=8,1 см, АВ:АС=11:9,
3) АВ=6 см, АС:СС1= 2:5,
4) АС=а, ВС=в, СС1=с.
Дано: АВ, А α, С АВ, СС1 ВВ1, С1,В1 α
Найти BB1