Функции y = tg x, y = ctg x, их свойства и графики

1.

y f (x)
у
х
Функции y = tg x, y = ctg x,
их свойства и графики.

2.

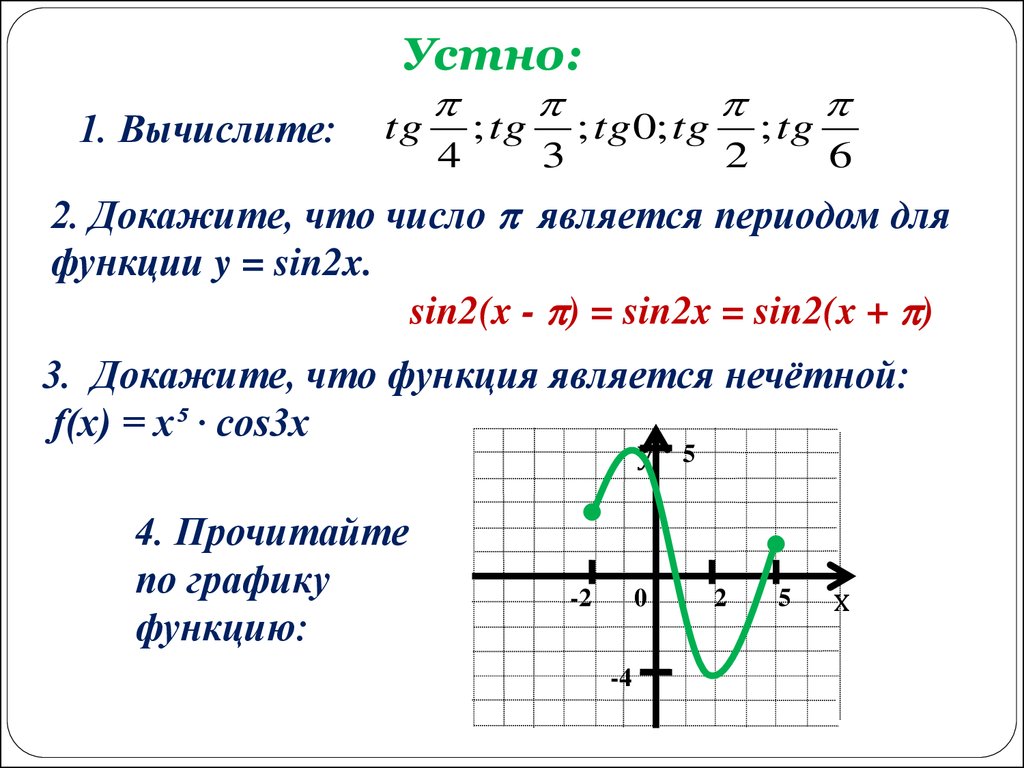
Устно:
1. Вычислите:
tg
4
; tg
3
; tg 0; tg
2
; tg
6
2. Докажите, что число является периодом для
функции y = sin2x.
sin2(x - ) = sin2x = sin2(x + )
3. Докажите, что функция является нечётной:
f(x) = x⁵ ∙ cos3x
у
4. Прочитайте
по графику
функцию:
-2
0
-4
5
2
5
х

3.

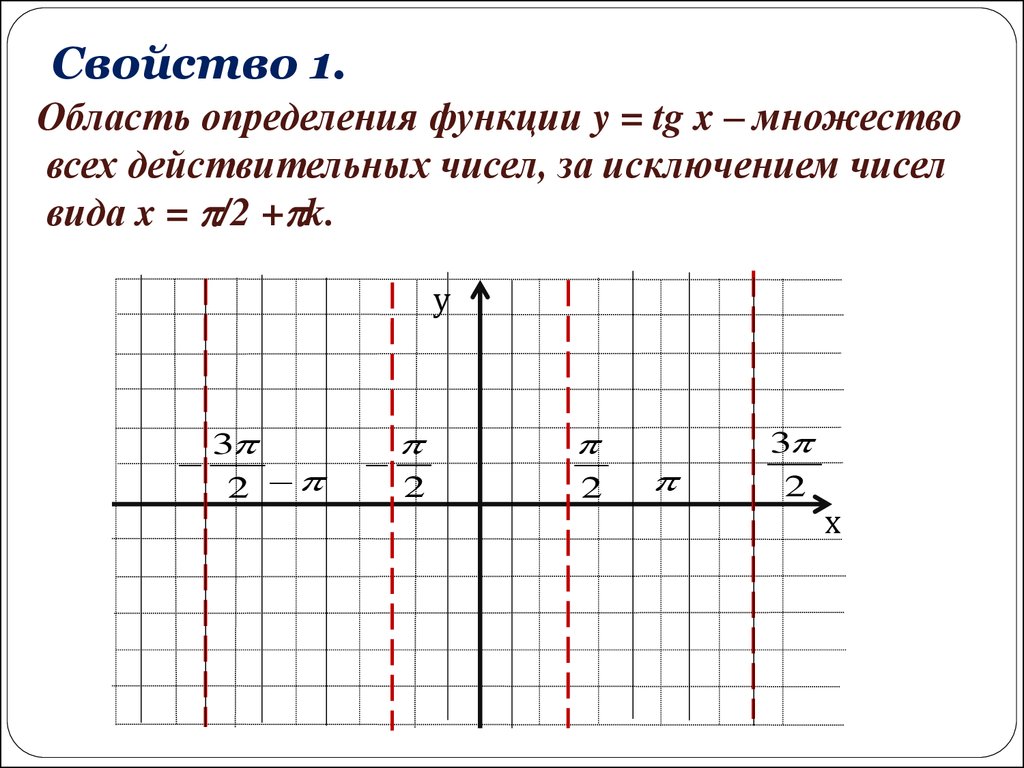
Свойство 1.
Область определения функции y = tg x – множество
всех действительных чисел, за исключением чисел
вида x = /2 + k.
у
3
2
2
2
3
2
х

4.

Свойство 2.
y = tg x – периодическая функция с
периодом .
tg(x - ) = tg x = tg(x + )
Свойство 3.
y = tg x – нечётная функция.
tg(- x) = - tg x
(График функции симметричен относительно
начала координат).

5.

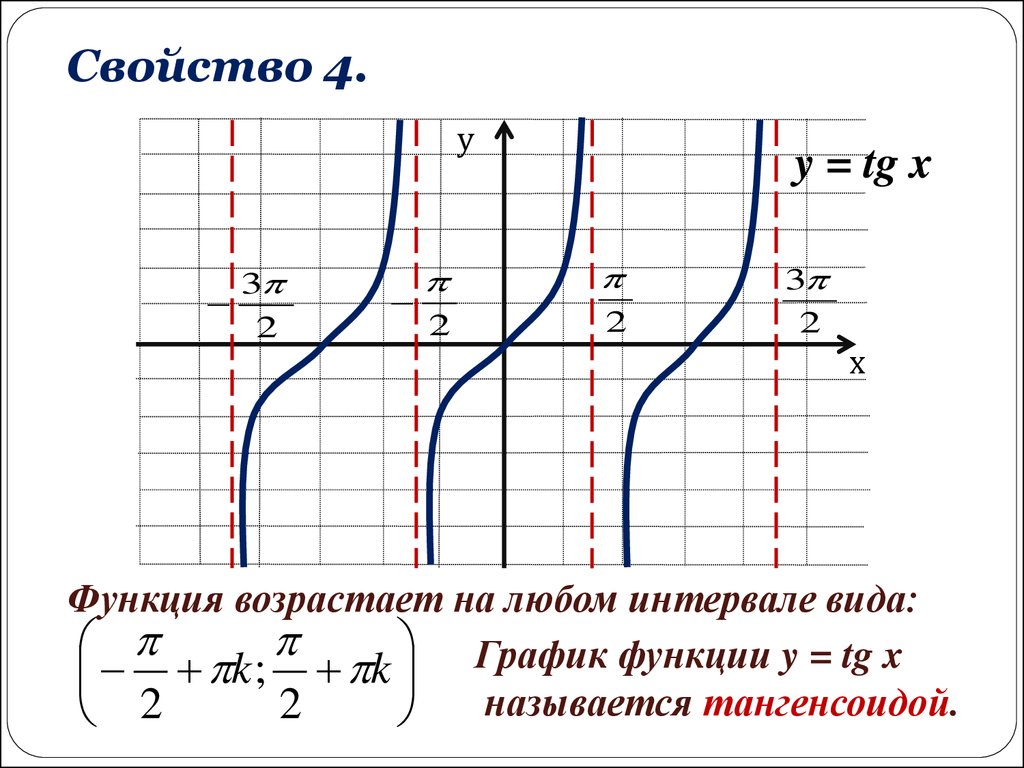
Свойство 4.
у
3
2
y = tg x
2
2
3
2
х
Функция возрастает на любом интервале вида:
График функции y = tg x
k ; k
называется тангенсоидой.
2
2

6.

Свойство 5.
Функция y = tg x не ограничена ни снизу, ни сверху.
Свойство 6.
У функции y = tg x нет ни наибольшего, ни
наименьшего значений.
Свойство 7.
Функция y = tg x непрерывна на любом интервале
вида
k ; k
2
2
Свойство 8.
E( f ) ;

7.

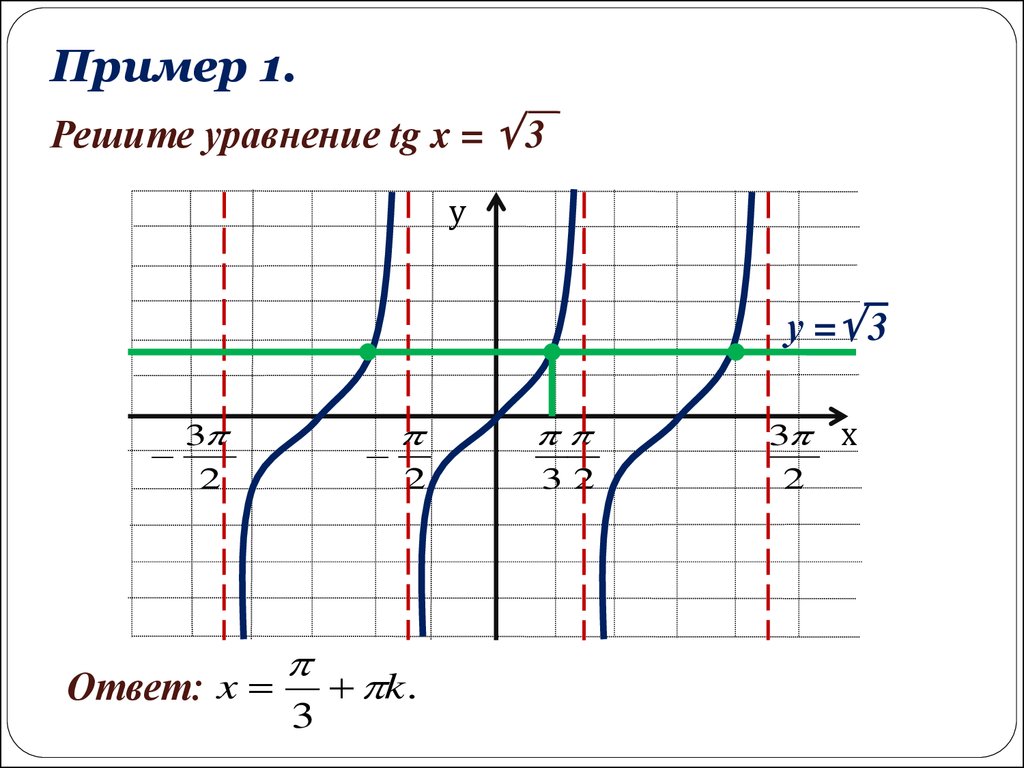
Пример 1.
Решите уравнение tg x = 3
у
у = 3
3
2
Ответ: x
3
2
32
k .
3 х
2

8.

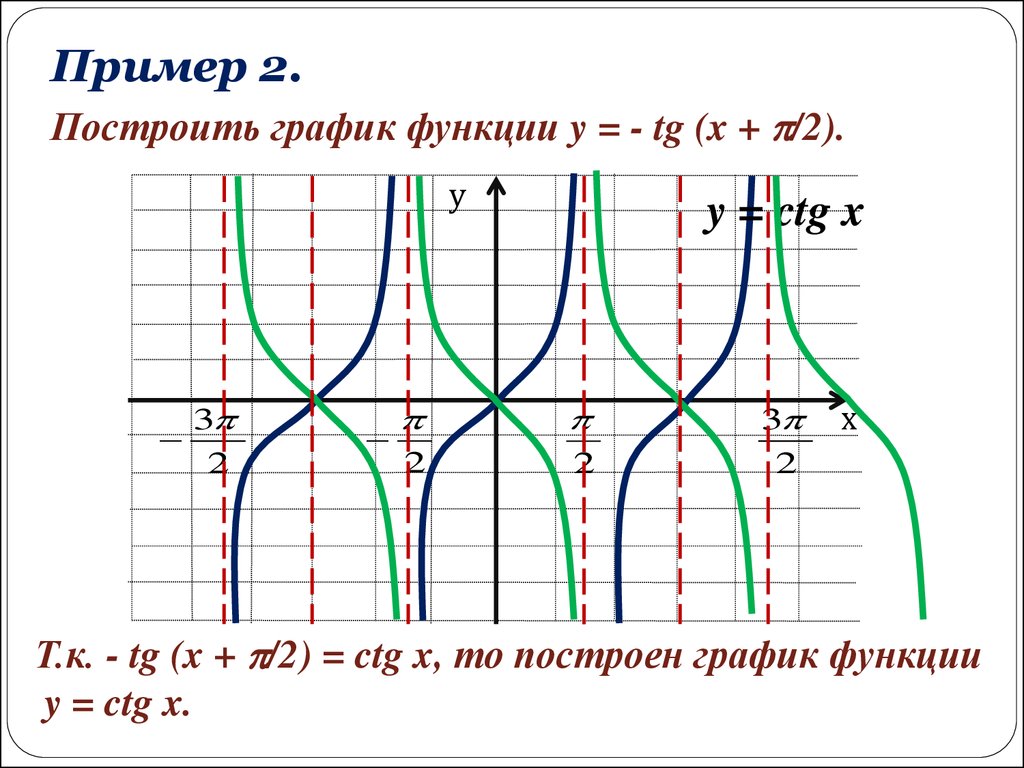
Пример 2.
Построить график функции y = - tg (x + /2).
у
3
2
y = ctg x
2
2
3
2
х
Т.к. - tg (x + /2) = ctg x, то построен график функции
y = ctg x.

9.

Опишите свойства функции y = ctgx.
1) D(f): множество всех действительных чисел, кроме чисел
вида x = k.
2) Периодическая с периодом .
3) Нечётная функция.
4) Функция убывает на любом интервале вида ( k; + k).
5) Функция не ограничена ни снизу, ни сверху.
6) Функция не имеет ни наибольшего, ни наименьшего
значений.
7) Функция непрерывна на любом интервале вида ( k; + k).
8) E(f) = (- ; + ).

10. Разберём примеры 1-3, с. 67-70

11. В классе:

№ 254
№ 255
№ 256 (а, б)
№ 259 (а, б)

12. Домашнее задание:

№ 256 (в, г)
№ 257
№ 259 (в, г)