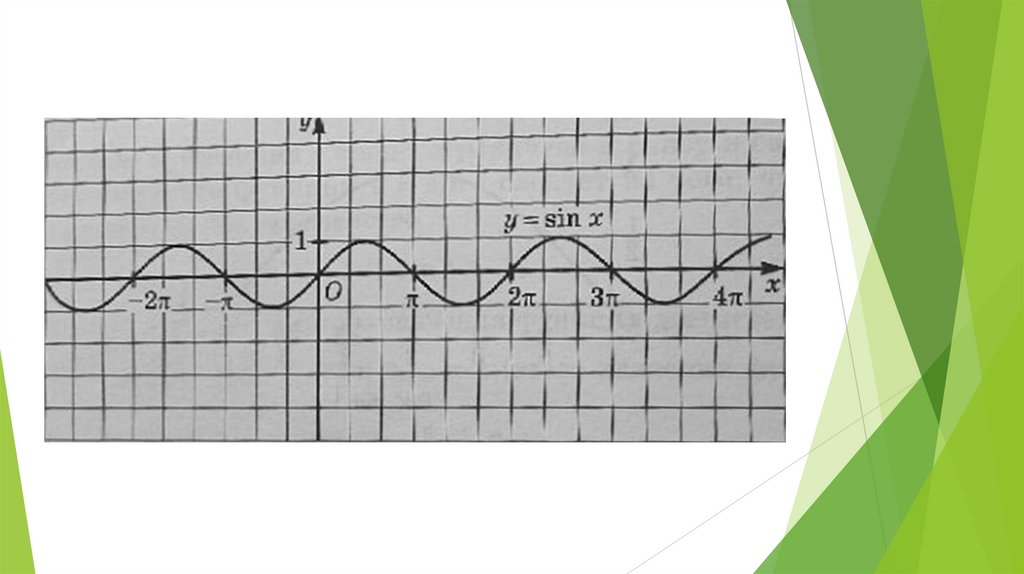
Функция y = sin x, ее свойства и график

1.

Функция y = sin x, ее свойства и график
Свойства функции y = sin t:
• Свойство 1: Область определения – множество R
действительных чисел
• Свойство 2: y = sin t – нечетная функция. График функции y =
sin t, как график любой нечетной функции, симметричен
относительно начала координат.Я

2.

Свойства функции y = sin t:
Свойство 3: Функция y = sin t – нечетная функция. [0;π/2] и
убывает на отрезке [π/2;π].
При движении точки по первой четверти числовой окружности (от 0
до π/2) ордината постепенно увеличивается (от 0 до 1), а при
движении по второй четверти числовой окружности (от π/2 до π)
ордината постепенно уменьшается (от 1 до 0)
Свойство 4: Функция s = sin t ограничена и снизу и сверху.
Ограниченность функции s = sin t следует из того, что для
любого t справедливо неравенство
-1 ⩽ sin t ⩽ 1.

3.

Свойства функции y = sin t:
Свойство 5: yнаим = -1 (этого значения функция достигает в
любой точке вида t = - π/2 + 2πk); sнаиб = 1 (этого значения
функция достигает в любой точке вида t = π/2 = 2πk).
Свойство 6: Функция y = sin x возрастает на любом отрезке
вида [-π/2 + 2πk; 3π/2 + 2πk], где k ∈ Z.

4.

Свойства функции y = sin t:
Свойство 7: y = sin x – непрерывная функция.
Непрерывность функции означает, что график функции сплошной, не имеет разрыва.
Свойство 8: Область значений функции – отрезок [-1; 1]

5.

6.

Функция y = cos x, ее свойства и график
Свойства функции y = cos x:
Свойство 1: D(f) = (-∞; ∞).
Свойство 2: y = cos x – четная функция.
Это следует из выведенной формулы cos (-t) = cos t.

7.

Свойства функции y = cos x:
Свойство 3: Функция убывает на отрезке [0;π], возрастает на
отрезке [π; 2π] и т.д.
Свойство 4: Функция ограничена и снизу и сверху

8.

Свойства функции y = cos x:
Свойство 5: yнаим = -1 (этого значения функция достигает в
любой точке вида x = π + 2 πk); yнаиб = 1 (этого значения
функция достигает в любой точке вида x = 2π).
Свойство 6: y = cos x – непрерывная функция.

9.

Свойства функции y = cos x:
Свойства 7. E(f) = [-1; -1].

10.

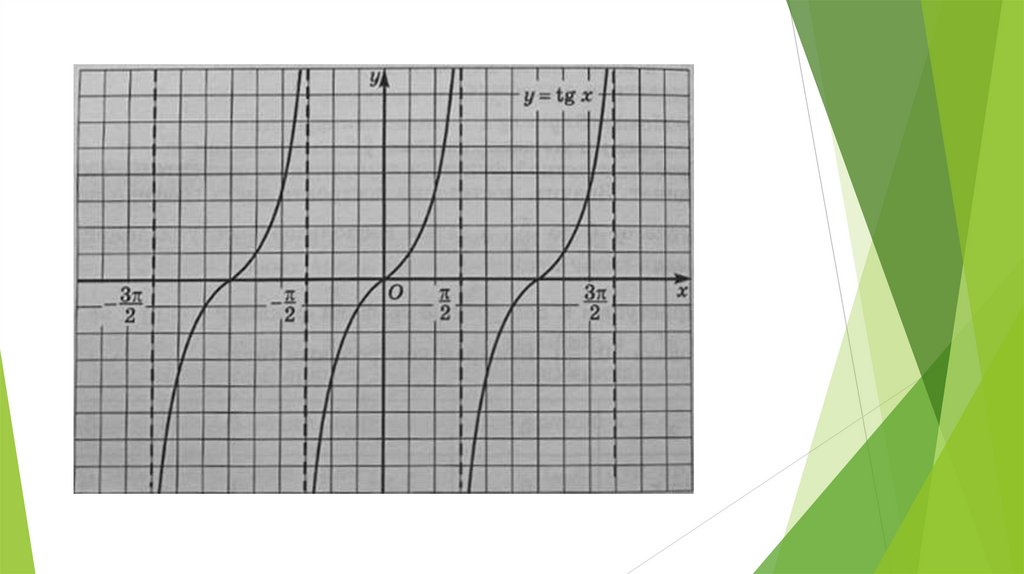
Функции y = tg x, их свойства и графики
• Свойство 1: Область определения функции y = tg x – множество
всех действительных чисел, за исключением чисел вида
X = π/2 + πk, k ∈ Z.
Это свойство означает, что на графике функции y = tg x нет точки, принадлежащей
прямой x = π/2, нет точки, принадлежащей прямой x = 3π/2
Свойство 2: y = tg x – периодическая функция с основным
периодом π.
То, что π – период, сделает из двойного равенства
tg(x-π) = tg x = tg(x+π),

11.

Функции y = tg x, их свойства и графики
• Свойство 3: y = tg x – нечетная функция
т.к. tg(-t) = -tg t.
• Свойство 4: Функция y = tg x возрастает на интервале (-π; π/2).
Вообще функция возрастает на любом интервале вида
(-π/2 + π/2 + πk); k ∈ Z.

12.

Функции y = tg x, их свойства и графики
• Свойство 5: Функция y = tg x не ограничена ни сверху, ни снизу
(это свойство иллюстрирует линия тангенсов).
• Свойство 6: У функции y = tg x нет ни наибольшего, ни
наименьших значений.

13.

Функции y = tg x, их свойства и графики
• Свойство 7: Функция y = tg x непрерывная на интервале вида (π/2; π/2).
Вообще функция непрерывная на любом интервале вида (- π/2 + π; π/2 + πk).
В точках x = π/2 + πk функция претерпевает разрыв. Каждая прямая вида x = π/2 + πk
служит вертикально асимптотой графика функции.
• Свойство 8: E(f) = (-∞; +∞).