Похожие презентации:
Понятие динамической системы станка. Динамическое качество станка. Основные задачи динамики станков
1. Динамика станков (лекции)
Молодцов В.В.Лекция № 1.
Понятие динамической системы станка.
Динамическое качество станка
Основные задачи динамики станков.
Статические и динамические характеристики элементов и систем.
Передаточная функция динамической системы станка.
2.
а)Рис. 1 Схема замкнутой динамической системы станка
б)
Рис. 2 Область неустойчивости при растачивании
3.
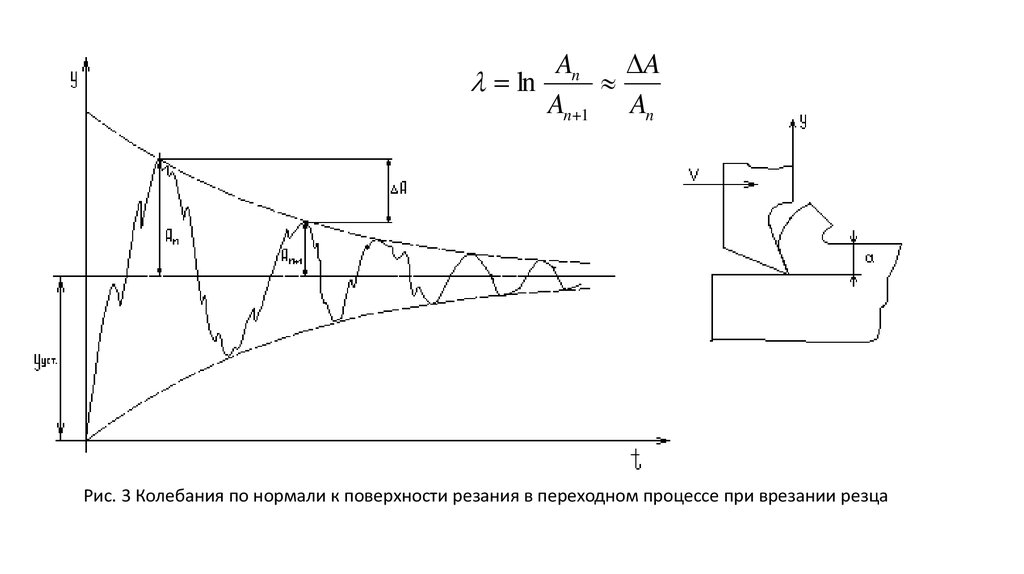
AnA
ln
An 1 An
Рис. 3 Колебания по нормали к поверхности резания в переходном процессе при врезании резца
4.
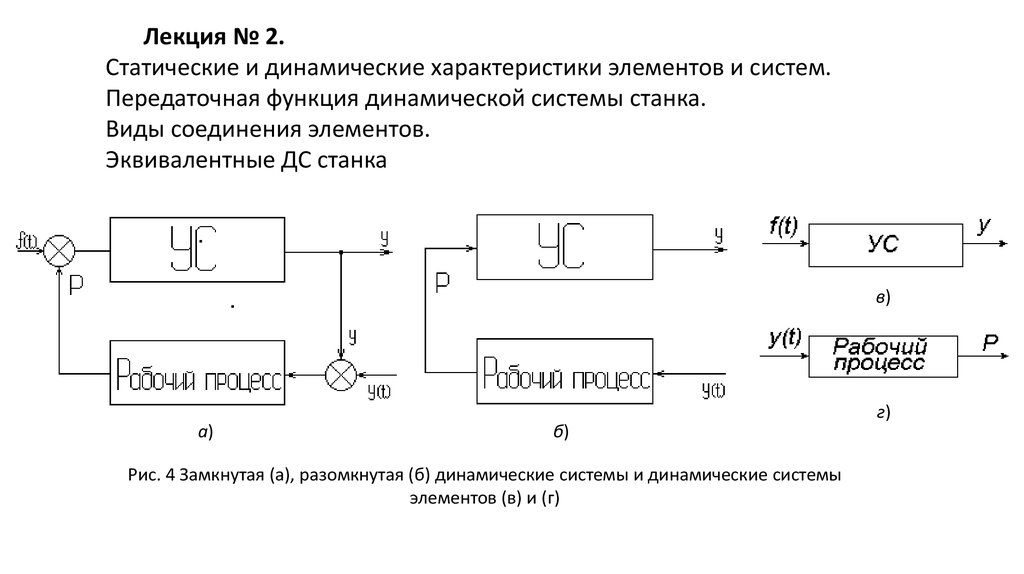
Лекция № 2.Статические и динамические характеристики элементов и систем.
Передаточная функция динамической системы станка.
Виды соединения элементов.
Эквивалентные ДС станка
в)
г)
а)
б)
Рис. 4 Замкнутая (а), разомкнутая (б) динамические системы и динамические системы
элементов (в) и (г)
5.
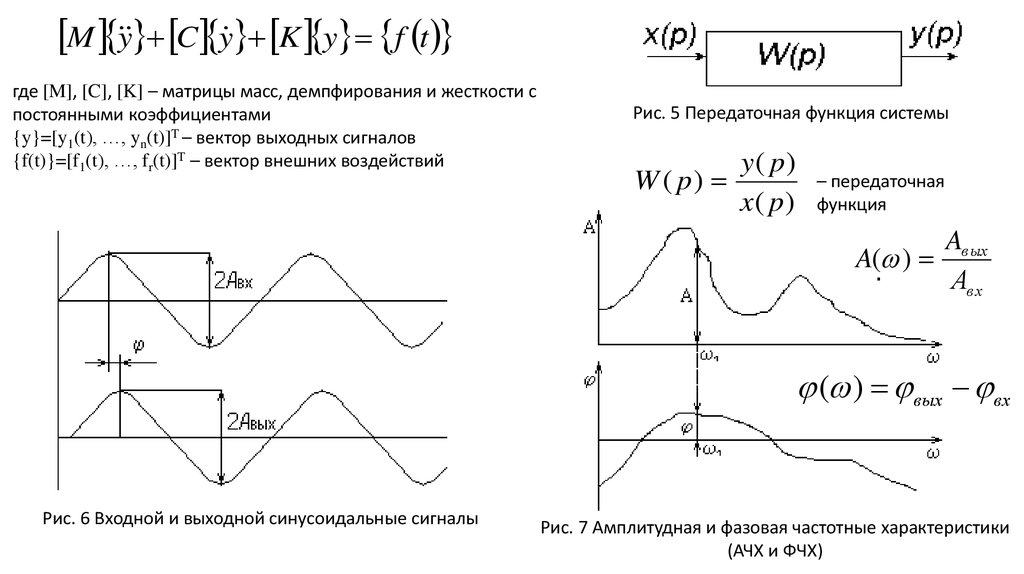
M y C y K y f tгде [M], [C], [K] – матрицы масс, демпфирования и жесткости с
постоянными коэффициентами
{y}=[y1(t), …, yn(t)]T – вектор выходных сигналов
{f(t)}=[f1(t), …, fr(t)]T – вектор внешних воздействий
Рис. 5 Передаточная функция системы
y( p)
W ( p)
x( p)
– передаточная
функция
Aвых
A( )
Авх
( ) вых вх
Рис. 6 Входной и выходной синусоидальные сигналы
Рис. 7 Амплитудная и фазовая частотные характеристики
(АЧХ и ФЧХ)
6.
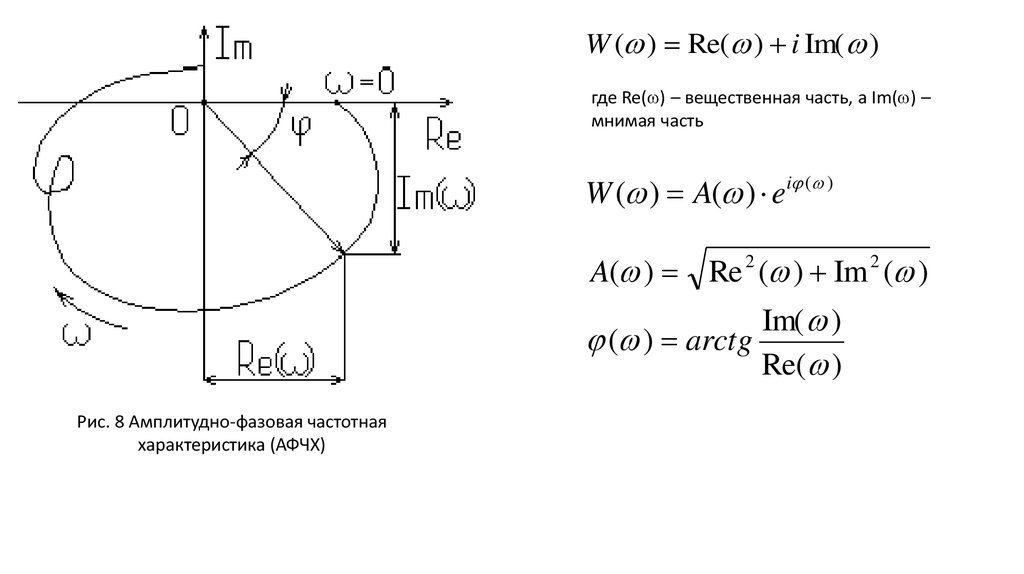
W ( ) Re( ) i Im( )где Re( ) – вещественная часть, а Im( ) –
мнимая часть
W ( ) A( ) ei ( )
A( ) Re ( ) Im ( )
2
Im( )
( ) arctg
Re( )
Рис. 8 Амплитудно-фазовая частотная
характеристика (АФЧХ)
2
7.
y ( )W
W1 ( ) W2 ( )
x( )
Рис. 9 Последовательное соединение звеньев
W W1 ( ) W2 ( )
а)
y ( ) y1 ( ) y2 ( )
W W1 ( ) W2 ( )
б)
Рис. 10 Параллельное соединение звеньев
y ( ) y1 ( ) y2 ( )
8.
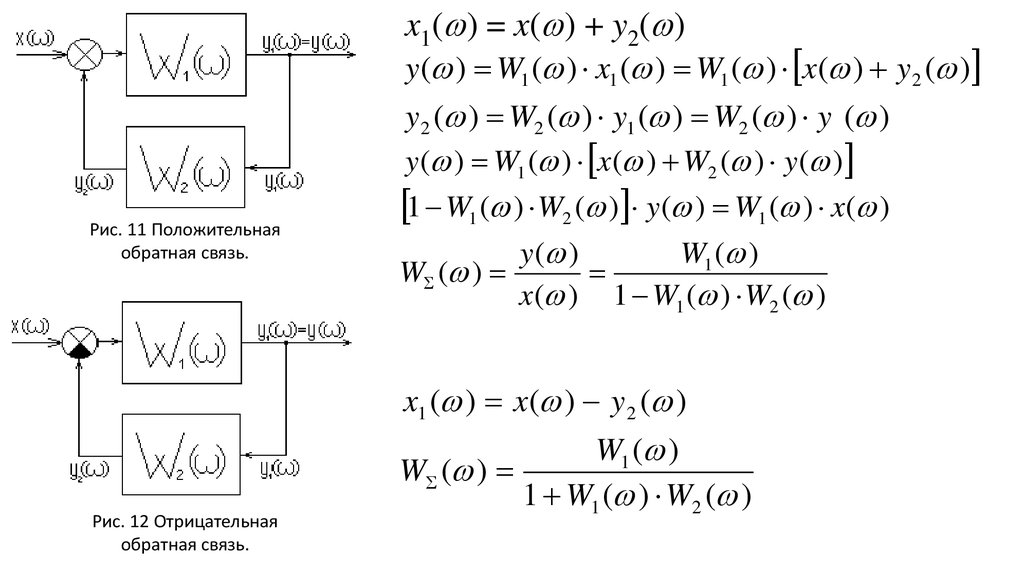
x1( ) = x( ) + y2( )y ( ) W1 ( ) x1 ( ) W1 ( ) x( ) y2 ( )
y2 ( ) W2 ( ) y1 ( ) W2 ( ) y ( )
y ( ) W1 ( ) x ( ) W2 ( ) y ( )
Рис. 11 Положительная
обратная связь.
1 W1 ( ) W2 ( ) y ( ) W1 ( ) x( )
y ( )
W1 ( )
W ( )
x( ) 1 W1 ( ) W2 ( )
x1 ( ) x ( ) y 2 ( )
Рис. 12 Отрицательная
обратная связь.
W1 ( )
W ( )
1 W1 ( ) W2 ( )
9.
Wдс. рез W ус ( ) W р ( )Рис. 13 Передаточные функции
динамической системы
Рис. 14 Механическая система
Wдс. f ( )
W ус ( )
W ус ( )
y ( )
f ( ) 1 W ус ( ) W р ( ) 1 Wдс. рез ( )
Wдс.t ( )
W ус ( ) W р ( )
Wдс. рез ( )
y ( )
t ( ) 1 W ус ( ) W р ( ) 1 Wдс. рез ( )
10.
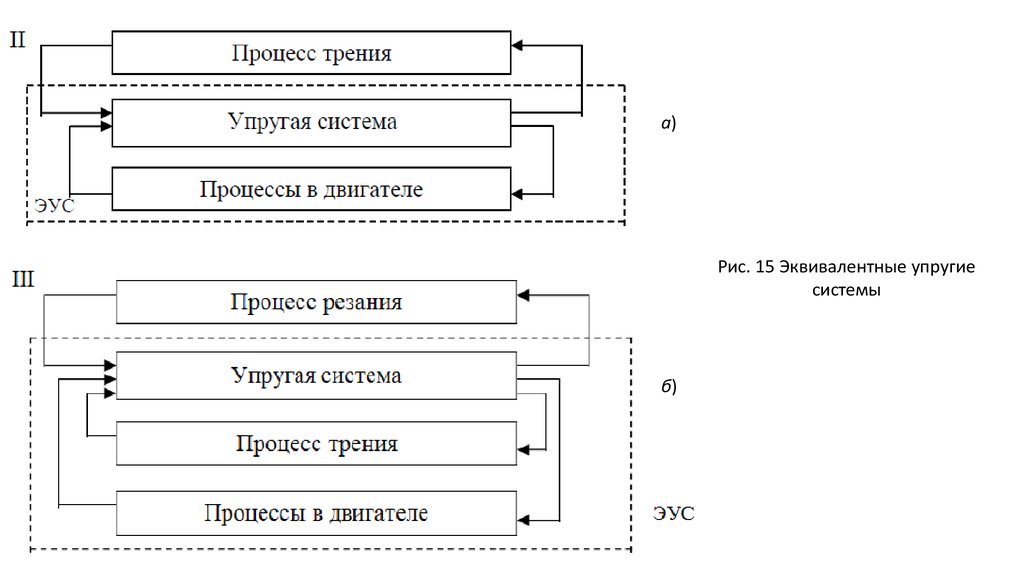
а)Рис. 15 Эквивалентные упругие
системы
б)
11.
Лекция № 3.Упругая система станка
,
Динамическая
податливость
Линеаризация
Wэус
y
[мм/Н], [мкм/Н]
P
1
P
y k эус y , где eэус и kэус – податливость
eэус
и жесткость системы
m y cy ky f (t )
e yc
e yc
y ( )
Wус ( )
2 2
f ( ) T1 p T2 p 1 T12 2 iT2 1
где р=i ; eyc=1/k – приведенная податливость системы (мм/Н или мкм/Н);
T1
Рис. 16 Простейшая УС с одной
степенью свободы
T2
m
1
– инерционная постоянная времени (сек);
k c
c
T1 – постоянная времени демпфирования (сек);
k
– логарифмический декремент;
с=2 fс – собственная круговая частота колебаний;
fс – собственная частота колебаний (Гц).
12.
Wyc ( ) Re yc ( ) i Im yc ( )Re yc ( )
Ayc ( ) Re ( ) Im ( )
2
yc
e yc (1 T )
2
1
2 2
2
(1 T12 ) T22 2
Im yc ( )
e ycT2
(1 T ) T
2
1
2 2
2
2
2
yc ( ) arctg
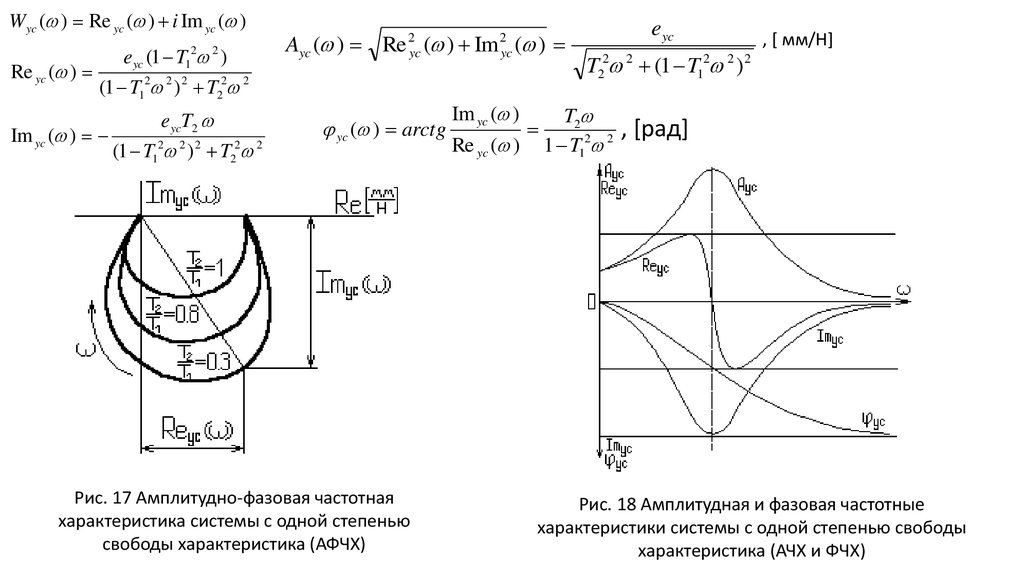
Рис. 17 Амплитудно-фазовая частотная
характеристика системы с одной степенью
свободы характеристика (АФЧХ)
2
yc
Im yc ( )
Re yc ( )
e yc
T22 2 (1 T12 2 ) 2
T2
1 T12 2
, [ мм/Н]
, [рад]
Рис. 18 Амплитудная и фазовая частотные
характеристики системы с одной степенью свободы
характеристика (АЧХ и ФЧХ)
13.
Линеаризацияр=с m, где – контактное перемещение, р – давление,
с и m – коэффициент и показатель степени
1
1
1
m
1 m ( p 0 p ) p0 m
c
1
( p0 p ) m p0
1
1
m
p0 m 1
p ...
m
1 1m
0
p mp
справедливо при р р0
c m k0
1
Рис. 19 Случай нагружения плоского стыка двух абсолютно жестких деталей
центрально приложенной, сосредоточенной силой Р и моментом М
bc m
P
( 0 L / 2) m 1 ( 0 L / 2) m 1 ,
( m 1)
bc m ( 0 L / 2) m 2 ( 0 L / 2) m 2 0 (( 0 L / 2) m 1 ( 0 L / 2) m 1 )
M 2
( m 2)
( m 1)
14.
mbL3c m 0m 1M
12
(m 1)( m 2) L2 2 (m 1)( m 2)( m 3)( m 4) L4 4
...
1
2
4
40 0
4480 0
L/2
P cb
m
x dx
0 /
L/2
M cb
m
x xdx
0 /
При
bc m
P
( 0 L / 2) m 1
( m 1)
bc m ( 0 L / 2) m 1
M
(( m 1) L / 2 0 )
2
( m 2)( m 1)
2(1 u) 0 / L , где u – безразмерная
неотрицательная переменная
bc m 0m L2
M
f (u )
4(m 2)( m 1)
Lk L/2+ 0/
Рис. 20 Случай работы стыка с частичным
раскрыванием ( 0 L/2 )
(2 u) m 1 (( m 1)u m)
f (u )
(1 u) 2
f (u)
500,0000
m=1
400,0000
m=1,5
300,0000
m=2
200,0000
Рис. 21 Графики f(u) для 100,0000
разных значений m
0,0000
u
0
2
4
6
8
10
15.
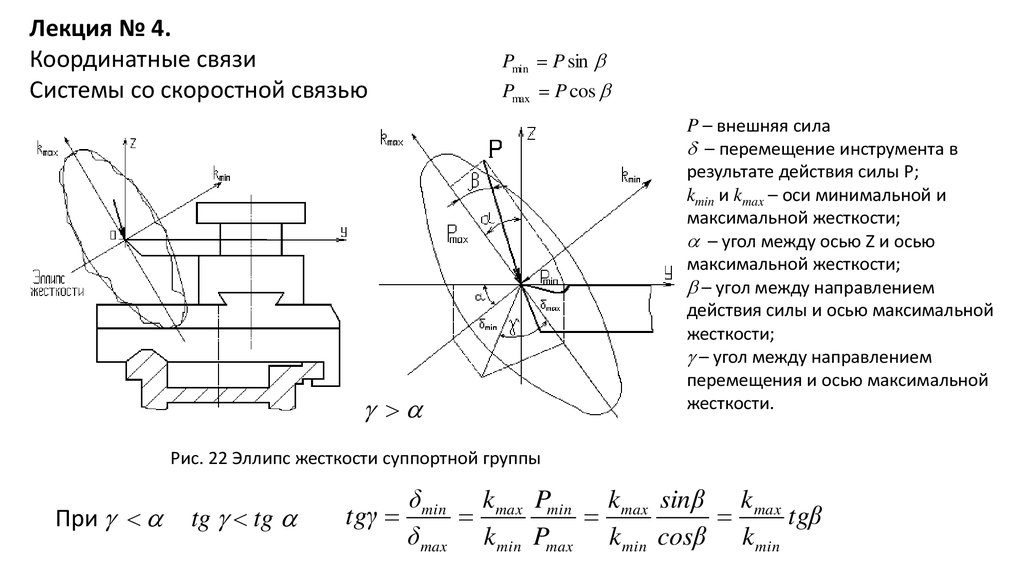
Лекция № 4.Координатные связи
Системы со скоростной связью
Pmin P sin
Pmax P cos
g a
P – внешняя сила
– перемещение инструмента в
результате действия силы P;
kmin и kmax – оси минимальной и
максимальной жесткости;
a – угол между осью Z и осью
максимальной жесткости;
– угол между направлением
действия силы и осью максимальной
жесткости;
g – угол между направлением
перемещения и осью максимальной
жесткости.
Рис. 22 Эллипс жесткости суппортной группы
При g a
tg g tg a
tgγ
δmin k max Pmin k max sinβ k max
tgβ
δmax k min Pmax k min cosβ k min
16.
ε1cosβ sinα sinβ cosα
Pmin
Pmax
ε2
P
P
cosα
sinα
y δmax sinα δmincosα
kmin
kmin
kmax
kmax kmin
kmax
ε1 cosβ sinα
ε2 sinβ cosα
eэус
y
ε
ε
1 2 0
P k max k min
m1q 1 c1q 1 k1q1 P cos
m2 q 2 c2 q 2 k 2 q2 P sin
где m1 и m2 – приведенные массы системы,
c1 и c2 – коэффициенты сил демпфирования,
k1=kmax и k2=kmin – главные жесткости системы
P
Τ p Τ 2 p 1 q1 cosβ
k1
2
1
2
Τ 1 2 p 2 Τ 2 p 1)q2
Рис. 23 Модель УС суппорта
Wэус
y q1 sin a q2 cosa
P
sinβ
κ2
y
ε1
ε2
2 2
P k1 T1 p T2 p 1 k 2 T1'2 p 2 T2' p 2 1
17.
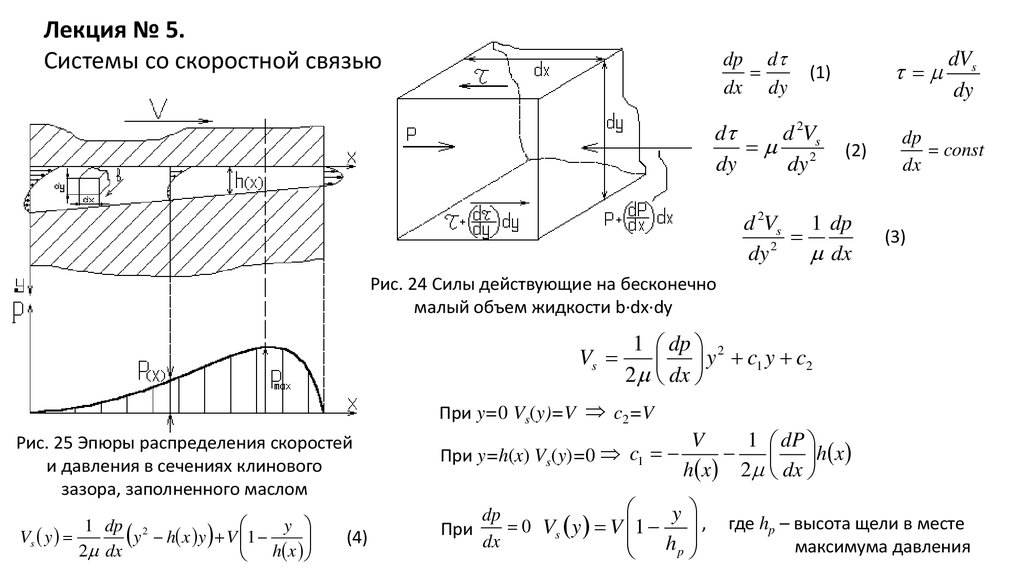
Лекция № 5.Системы со скоростной связью
dp d
dx dy
(1)
d 2Vs
d
dy
dy 2
(2)
d 2Vs 1 dp
2
dy
dx
dVs
dy
dp
const
dx
(3)
Рис. 24 Силы действующие на бесконечно
малый объем жидкости b·dx·dy
Vs
1 dp 2
y c1 y c2
2 dx
При y=0 Vs(y)=V c2=V
Рис. 25 Эпюры распределения скоростей
и давления в сечениях клинового
зазора, заполненного маслом
Vs y
1 dp 2
y h x y V 1 y
2 dx
h x
(4)
При y=h(x) Vs(y)=0 c1
V
1 dP
h x
h x 2 dx
y
dp
,
0 Vs y V 1
При
dx
hp
где hp – высота щели в месте
максимума давления
18.
6 Vl 2bF
K F F K ГV
h02
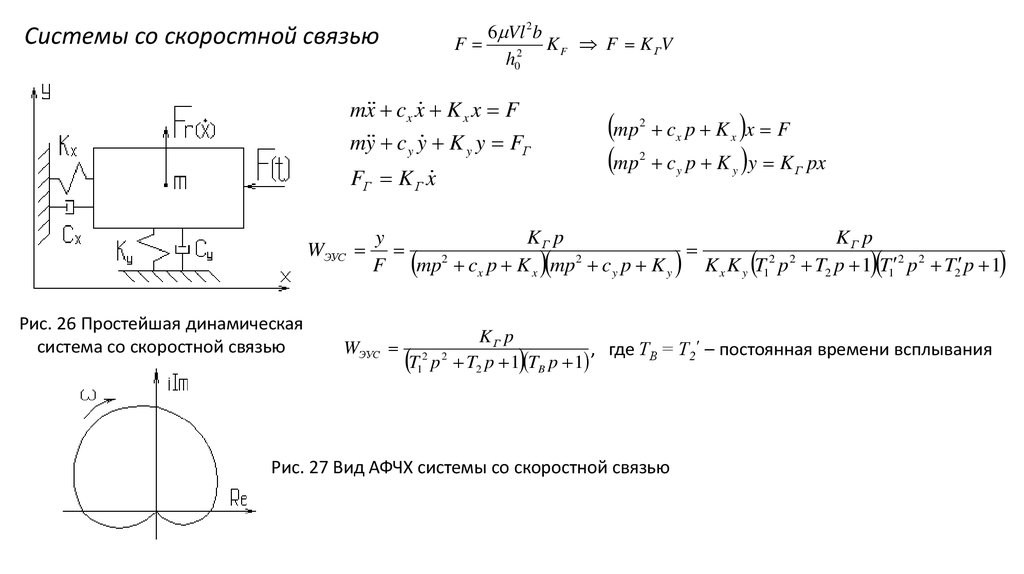
Системы со скоростной связью
m x cx x K x x F
m y c y y K y y FГ
FГ K Г x
WЭУС
Рис. 26 Простейшая динамическая
система со скоростной связью
mp
mp
2
2
cx p K x x F
c y p K y y K Г px
y
KГ p
KГ p
F mp2 cx p K x mp2 c y p K y K x K y T12 p 2 T2 p 1 T1 2 p 2 T2 p 1
WЭУС
KГ p
, где ТВ = Т2ꞌ – постоянная времени всплывания
2 2
T1 p T2 p 1 TB p 1
Рис. 27 Вид АФЧХ системы со скоростной связью
19.
Лекция № 6.Инерционная связь
Рабочие процессы
Процесс трения
Fж Fg FИН F
Fж K x x0
FИН m x c m x 0 mh 0
Fg cx x 0
M ж M g M ИН 0
xc x0 h 0
M ж K 0
M g c 0
M ИН J c 0 FИН h J c 0 mh x 0 h 0 J c mh2 0 mh x 0 J 0 0 mh x 0
Рис. 28 Простейшая динамическая
система с инерционной связью
m x 0 mh 0 cx x 0 K x x0 F (t )
(1)
J 0 0 mh x 0 c 0 K 0 0
(2)
m p cx p K x x0 p mhp2 0 p F p
J 0 p 2 c p K 0 p mhp2 x0 p 0
0 p
mh0
KF p2
,
где
K
WЭУС p
F
4
2 2
2 2
K x K
F p K F mh0 p T1 p T2 p 1 T1 p T2 p 1
Рис. 29 Вид АФЧХ системы с
инерционной связью
20.
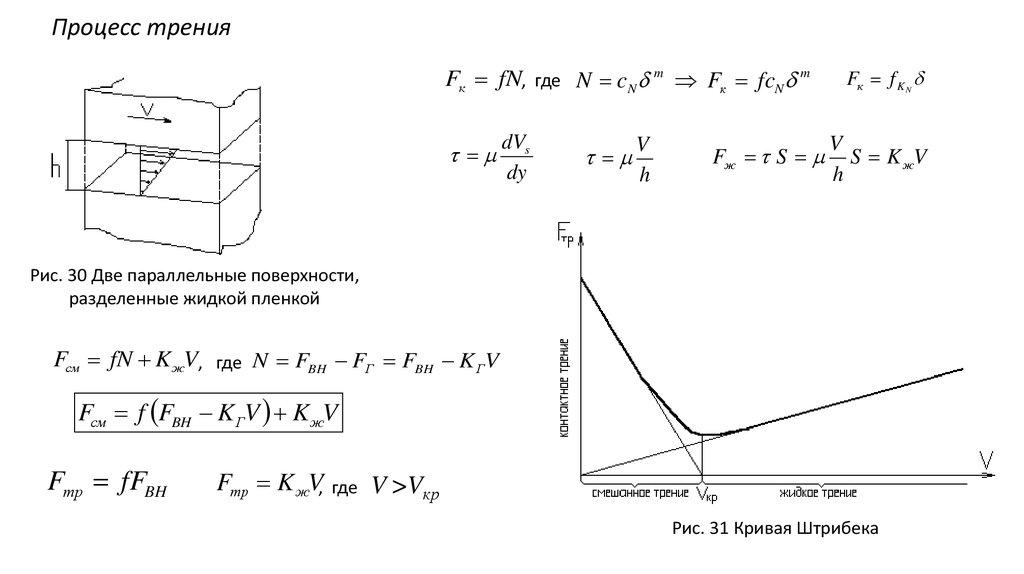
Процесс тренияFк fN, где N c N m Fк fcN m
dVs
dy
V
h
Fж S
Fк f K N
V
S K жV
h
Рис. 30 Две параллельные поверхности,
разделенные жидкой пленкой
Fсм fN K жV, где N FBH FГ FBH K ГV
Fсм f FBH K ГV KжV
Fтр fFBH
Fтр K жV,
где
V >Vкр
Рис. 31 Кривая Штрибека
21.
T2
1
p 2 T2 p 1 x
Fтр
1
2
Fтр Fтр
Fтр
fKN y K ж x
Kx
T1 2 p 2 T2 p 1 y K Г px
Ky
F(Тр1) fKN y КT y
Fтр
T1 2 p 2 T2 p 1
px , где
KT K Г
Ky
F p
WT p
px p TB p 1
tg CT
ст
Рис. 32 Геометрический смысл
постоянной
Практическое воздействие на процесс трения осуществляется следующими
путями:
• Подбором материалов трущихся тел;
• Введением новых видов смазки;
• Изменением геометрии профилей контактирующих поверхностей;
• Изменением нормальной нагрузки к поверхности.
Лекция № 7.
Процесс резания
Устойчивость перемещения узлов станка
Устойчивость динамической системы станка
при резании
22.
Процесс резанияP
Kp
1 Tp p
y
K p k в b0
a
Tp k
U
а)
б)
Рис. 33 Вид стружки и колебания силы резания:
а) - при образовании стружки надлома; б) - при
формировании периодически срывающегося
нароста
Рис. 34 Усадка стружки
Kр
Kр
K рTр
P p
WP p
i
y p 1 iT р 1 Tр2 2
1 Tр2 2
Рис. 35 АФЧХ процесса резания
a1
a
23.
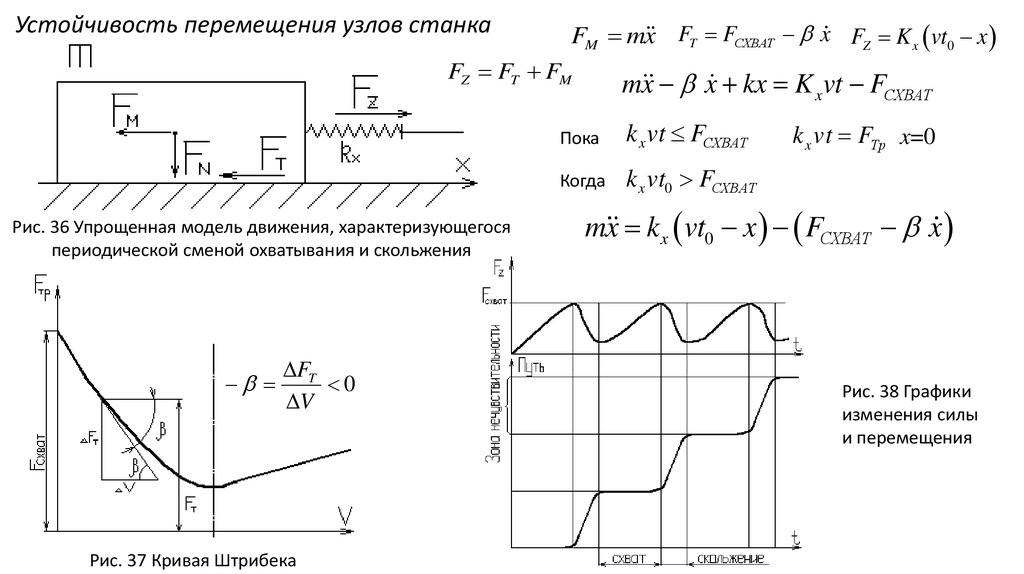
Устойчивость перемещения узлов станкаFM m x FT FСХВАТ x FZ K x vt0 x
FZ FT FM
Рис. 36 Упрощенная модель движения, характеризующегося
периодической сменой охватывания и скольжения
FT
0
V
Рис. 37 Кривая Штрибека
mx x kx K xvt FСХВАТ
Пока
k x vt FСХВАТ
Когда
k x vt0 FСХВАТ
k x vt FТр x=0
mx kx vt0 x FСХВАТ x
Рис. 38 Графики
изменения силы
и перемещения
24.
Устойчивость динамической системы станка при резании.Pполн kP a0 y kP a0 kP y PCT P
Wэус W1 W2
P k P y – динамическая составляющая
силы резания
m1q1 c1q1 k1q1 P cos k P y cos
m2q2 c2q2 k2q2 P sin k P y sin
kP y
T
p
T
p
1
q
cos
1 c
2
1
k
y
T1 2 p 2 T2 p 1 q2 cP sin
2
2
2
2
W1
y1
cos sin a
P
C1 T12 p 2 T2 p 1
W2
y2
sin cos a
P C2 T1 2 p 2 T p 1
Рис. 39 УС с двумя степенями свободы
с координатной связью
y q2 cosa q1 sin a y2 y1
z q1 cosa q2 sin a
Рис. 40 Структурная схема,
полученной динамической системы
25.
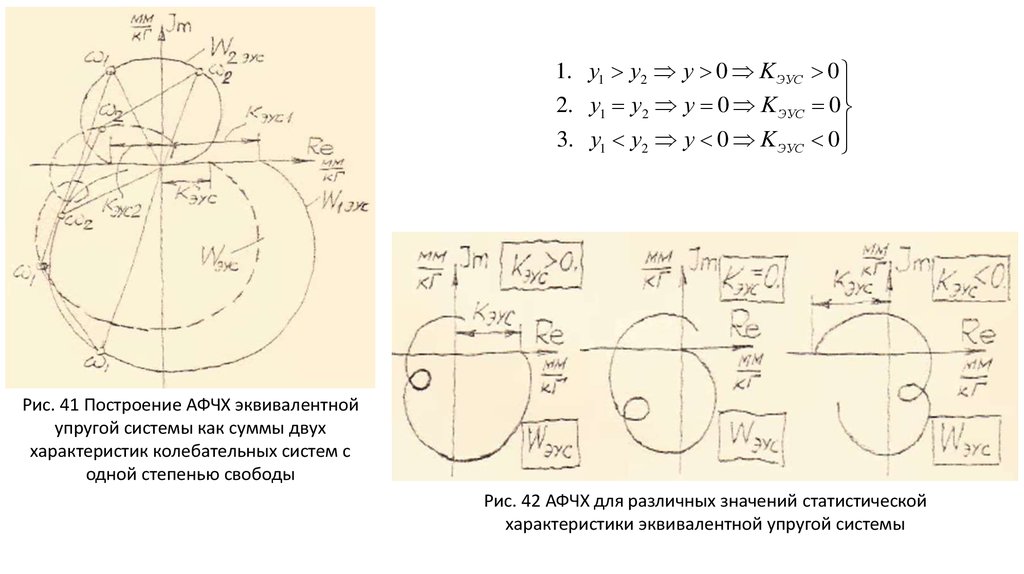
1. у1 у2 y 0 K ЭУС 02. у1 у2 y 0 K ЭУС 0
3. у1 у2 y 0 K ЭУС 0
Рис. 41 Построение АФЧХ эквивалентной
упругой системы как суммы двух
характеристик колебательных систем с
одной степенью свободы
Рис. 42 АФЧХ для различных значений статистической
характеристики эквивалентной упругой системы
26.
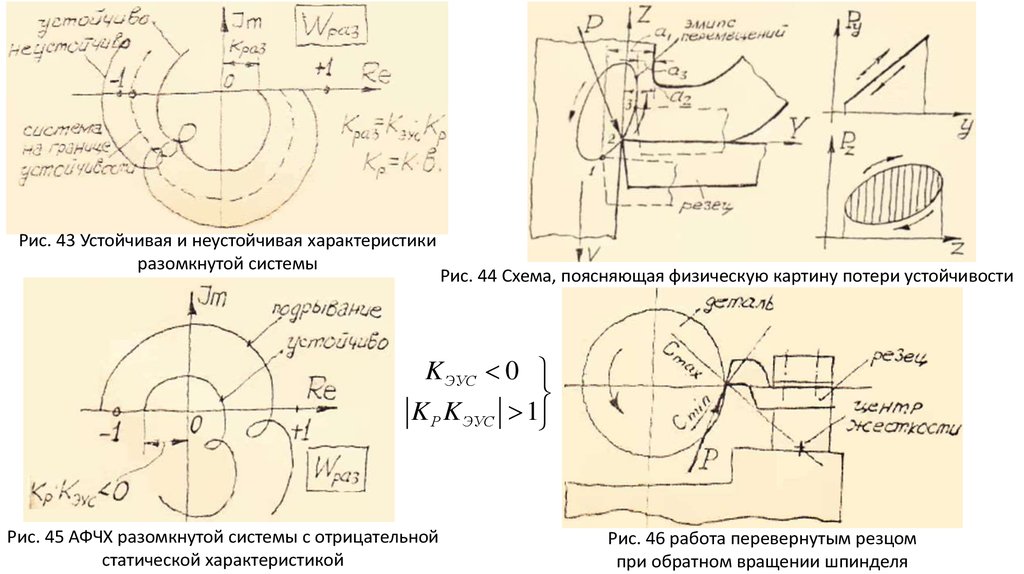
Рис. 43 Устойчивая и неустойчивая характеристикиразомкнутой системы
Рис. 44 Схема, поясняющая физическую картину потери устойчивости
K ЭУС 0
K Р K ЭУС 1
Рис. 45 АФЧХ разомкнутой системы с отрицательной
статической характеристикой
Рис. 46 работа перевернутым резцом
при обратном вращении шпинделя
27. Влияние динамической характеристики резания на поведение системы
Рис. 47 Зависимость силы резания отизменения толщины срезаемого слоя
Рис. 48 АФЧХ эквивалентной
упругой системы и процесса
резания
Рис. 49 Примеры АФЧХ устойчивой и
неустойчивой динамических систем
Wраз WЭУС WР AЭУС AР e
i ЭУС Р
28. Устойчивость динамической системы станка при резании «по следу»
Рис. 51 Схема эквивалентной динамической системы срезанием при обработке «по следу»: а) – замкнутая,
б) – разомкнутая.
Рис. 50 Схема резания широким
резцом с поперечной подачей.
Wy
Wраз
1 Wраз
W e i
29.
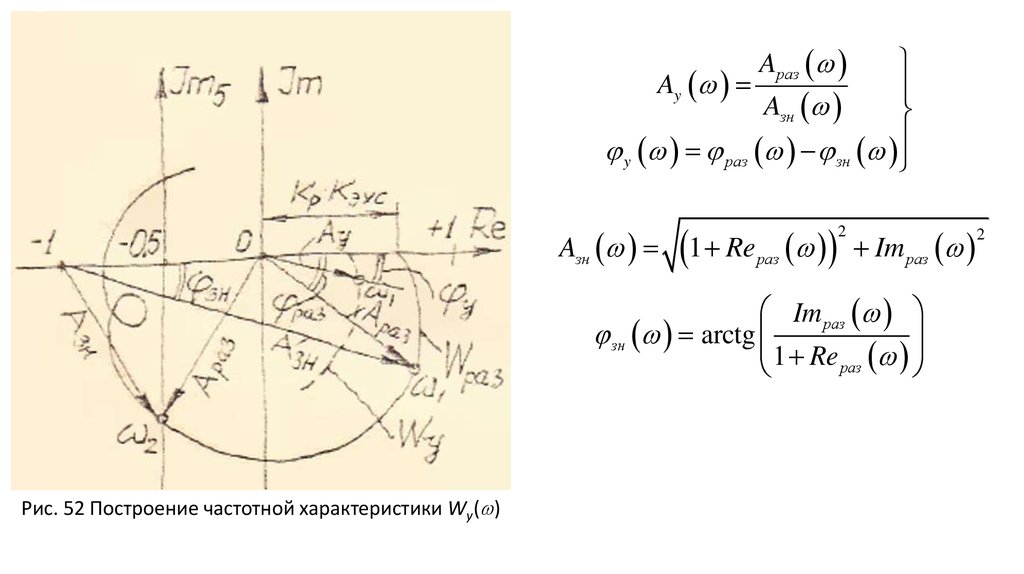
AразAy
Aзн
y раз зн
Aзн
1 Re
раз
2
Im раз
Im раз
зн arctg
1 Re
раз
Рис. 52 Построение частотной характеристики Wу ( )
2
30.
WразWy W
Если
Рис. 53 Построение характеристики
разомкнутой системы с запаздыванием.
60
nz
Ay 1 то Aраз Aзн
Рис. 54 Примеры характеристик систем, устойчивых и
неустойчивых при обработке «по следу».
31. Автоколебания при неустойчивом процессе стружкообразования
Рис.56 Простейшая модельдинамической системы при
резании на режимах
образования нароста
Рис. 55 Изменение температуры в
поверхностном слое стружки,
примыкающем к резцу, и в зоне сдвига
Рис. 57 Схема динамической
системы станка с учетом
наростообразования
Режим I – K p K ЭУС
Kp
Режим II – K p K ЭУС
Kp
Cy
Cy
1
1
32. Отклонения системы при внешних воздействиях
б)а)
Рис. 58 Схема замкнутой эквивалентной динамической системы
станка при внешних воздействиях: а) – на эквивалентную
упругую систему станка – f(t), б) – на процесс резания – y(t).
W fЭУС p
W fЭУС p
y p
Wf p
ft p 1 Wраз p Wзн p
W раз p
W раз p
y p
Wy p
y y p 1 W раз p Wзн p
W fЭУС p
y * p
ft p
Рис. 59 Получение характеристики
знаменателя выражений – Wзн(p)
Aзн
1 Reраз Imраз
2
Im раз
зн arctg
1 Re
раз
2
33.
Статические отклоненияРис. 61 Соответствующая ей схема
замкнутой системы (характеристика
1 – при положительном,
характеристика – 2 при
отрицательном коэффициенте)
Рис. 60 Схема обработки при
врезной подаче
y 0 yt 0 Wy 0
Здесь yt(0) =a0 является настройкой системы, а y(0) деформацией –
отклонением системы в направлении оси Y
y 0 a0 0 Wy 0 a0
K ЭУС K Р
1 K ЭУС K Р
34.
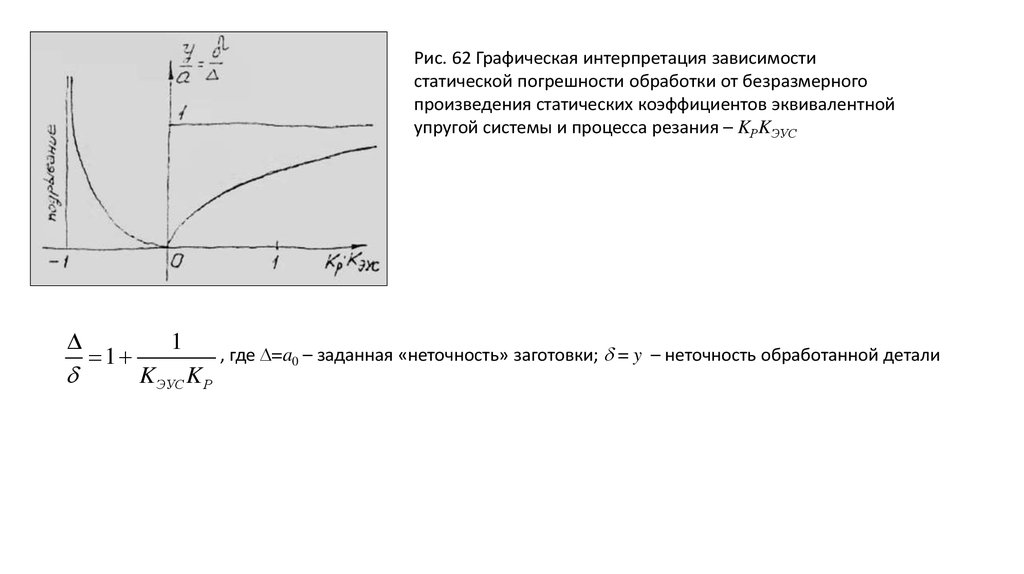
Рис. 62 Графическая интерпретация зависимостистатической погрешности обработки от безразмерного
произведения статических коэффициентов эквивалентной
упругой системы и процесса резания – KРKЭУС
1
1
K ЭУС K Р
, где =a0 – заданная «неточность» заготовки; = y – неточность обработанной детали
35.
q1 Q1cos t 1q2 Q2 cos t 2
1 2 0
1 2
2
1 2
q1 Q1 cos t
Pds ( P dy P dz )
q2 Q2 cos t
y
L
q1 Q1cos t
q2 Q2 cos t Q2 sin t
2
q1 Q1cos t
2 q2 Q2cos t Q2 sin t
2
L
q1 Q1cos 1
q2 Q2 cos 1
Z
36.
y Q1sin a cos 1 Q2 cosa cos 2z Q1cosa cos 1 Q2 sin a cos 2
dy Q1sin a sin 1 d Q2 cosa sin 2 d
dz Q1cosa sin 1 d Q2 sin a sin 2 d
Py k P sin a y k P sin a Q1sin a cos 1
k P sin a Q2 cosa cos 2
Pz k P cos a y k P cos a Q1sin a cos 1
k P cos a Q2 cosα cos 2
P dy P dz k
y
L
Q1sinα
z
2π
P
sin α β Q1sinα cos 1 Q2 cosα cos 2
0
2π
sin 1 Q2 cosα sin 2 d k P cos α β Q1sinα cos 1
0
Q2 cosα cos 2 Q1cosα sin 1 Q2 sinα sin 2 d
0 πk P Q1Q2 cos α β sin 1 2
APY 0
APZ πk P Q1Q2 cos α β sin 1 2


















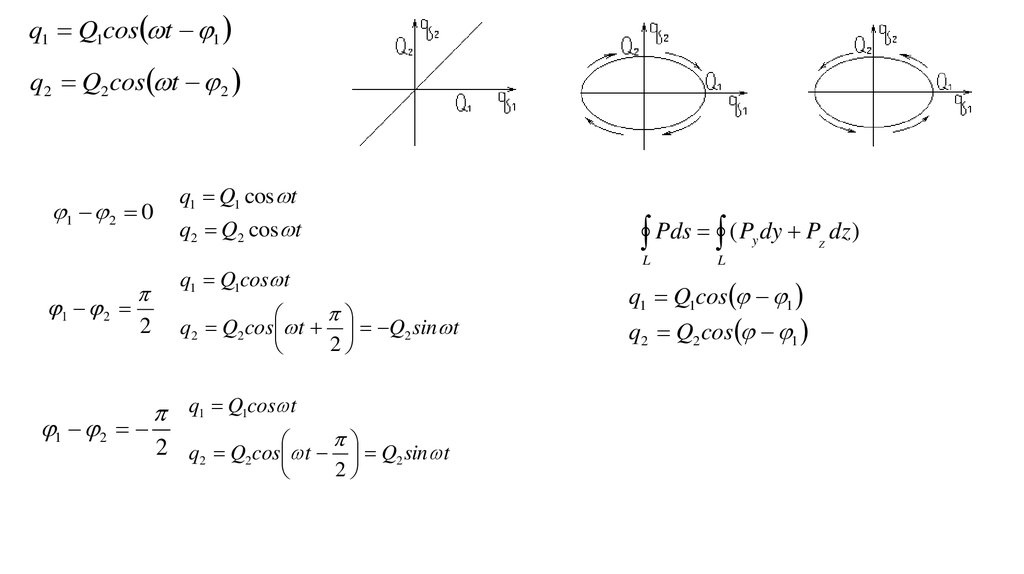

 Промышленность
Промышленность








