Похожие презентации:
Проекции. Центральные и параллельные проекции
1. Проекции
В общем случае проекции преобразуютточки, заданные в системе координат
размерностью n, в системы координат
размерностью меньше чем n.
Проекция трехмерного объекта строится
при помощи прямых проекционных
лучей, которые называются
проекторами и которые проходят
через каждую точку объекта и,
пересекая картинную плоскость,
образуют проекцию.
2. Центральные и параллельные проекции
картиннаяплоскость
проекторы
А
центр
проекции
В
А
А
В
A
центр
проекции в
бесконечности
В
А
В
A
3. Классификация
проекциипараллельные
центральные
одноточечная
ортогогональные
косоугольные
вид спереди
вид сбоку
вид сверху
аксонометрические
двухточечная
изометрическая
Кабине
трехточечная
диметрическая
Кавалье
4. Определения
Ортогональные проекции – это проекции, которыестроятся проекционными лучами падающими
перпендикулярно к КП (направление проецирования
совпадает с нормалью к КП).
Аксонометрическая проекция - предмет с системой
координат, проецируют на КП таким образом, чтобы эта
плоскость не совпадала с его координатной плоскостью.
Косоугольные проекции – направление
проецирования
и нормаль к КП не совпадают.
картинная
плоскость
Направление
проецирования
Направление
проецирования
проекция
проекция
ортографические проекции
косоугольные проекции
5. Изометрическая проекция
yz
x
Изометрическая проекция – нормаль к КП, (а
следовательно и направление проецирования) составляет
равные углы с каждой из главных координатных осей.
Изометрическая проекция обладает следующим свойством:
все 3 главные координатные оси одинаково укорачиваются.
Поэтому можно проводить измерения вдоль направления осей
с одним и тем же масштабом.
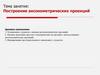
6. Диметрия
Диметрическаяпроекция — это
аксонометрическая
проекция, у которой
коэффициент искажения
по двум осям имеет
равное значение,
искажение по третьей оси
может принимать иное, не
равное значение.
Триметрическая
проекция — это
аксонометрическая
проекция, у которой
коэффициент искажения
7. Косоугольные проекции
Нормаль к КП и направление проецирования несовпадают. КП перпендикулярна главной
координатной оси, поэтому сторона объекта,
параллельная этой плоскости, проецируется так,
что можно измерить углы и расстояния.
Проецирование других сторон объекта также
допускает проведение линейных измерений (но не
Y
Кавальевдоль главных
угловых)
осей.
Y
Кабине
l
l
l
z
z
45
x
l/2
26,5
x
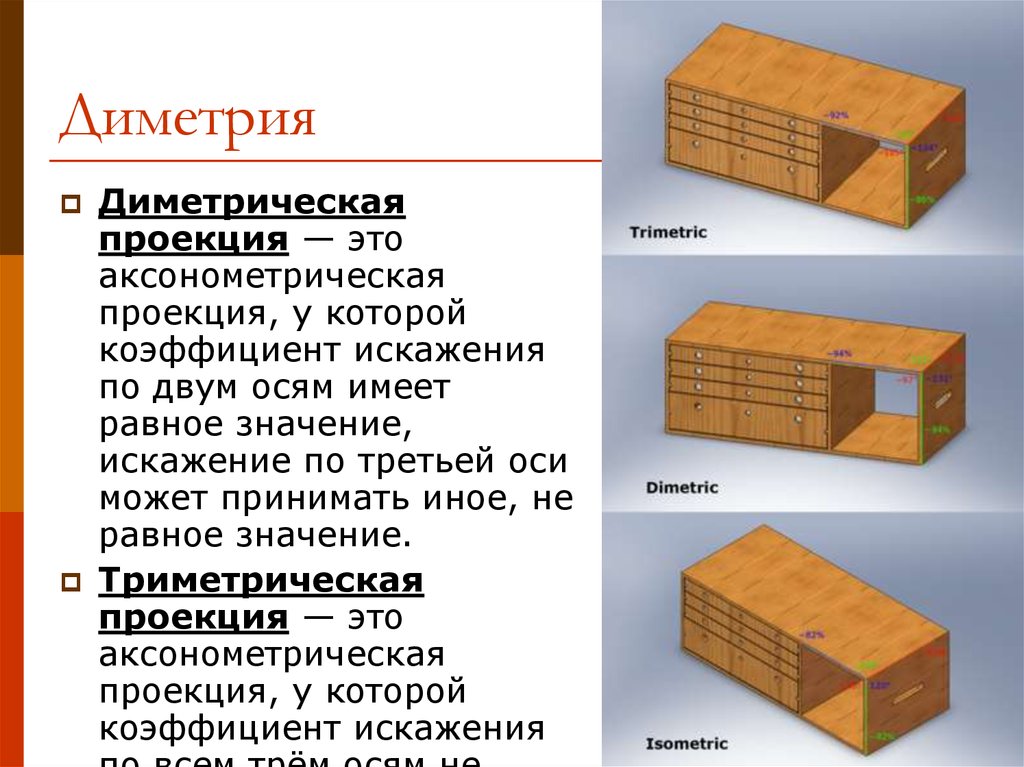
8. Точки схода
Центральная проекция любой совокупностипараллельных прямых, которые не
параллельны проекционной плоскости, будет
сходиться в точке схода. Точек схода
бесконечно много. Если совокупность прямых
параллельна одной из главных координатных
осей, то их точка схода называется главной
точкой схода.
9. Классификация центральных проекций
Центральные проекцииклассифицируются в зависимости от
числа главных точек схода, которыми
они обладают, а следовательно и от
числа координатных осей, которые
пересекают проекционную плоскость.
Существуют следующие перспективные
проекции:
Одноточечные
Двухточечные
Трехточечные
10. Пример перспективных проекций
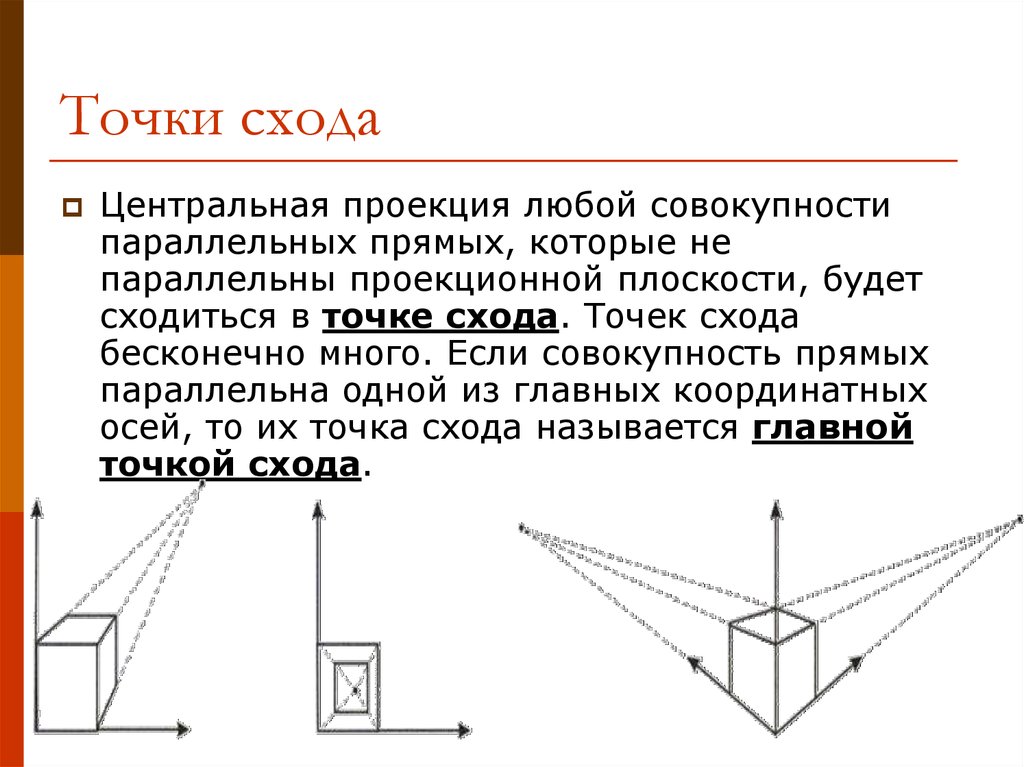
11. Примеры
12. Получение перспективной проекции
КП перпендикулярна оси Z и совпадаетс плоскостью Z = 1/r = d. Центр
проекции находится в центре координат.
1
0
M центральное1
0
0
0 0 0
1 0 0
0 1 r
0 0 0
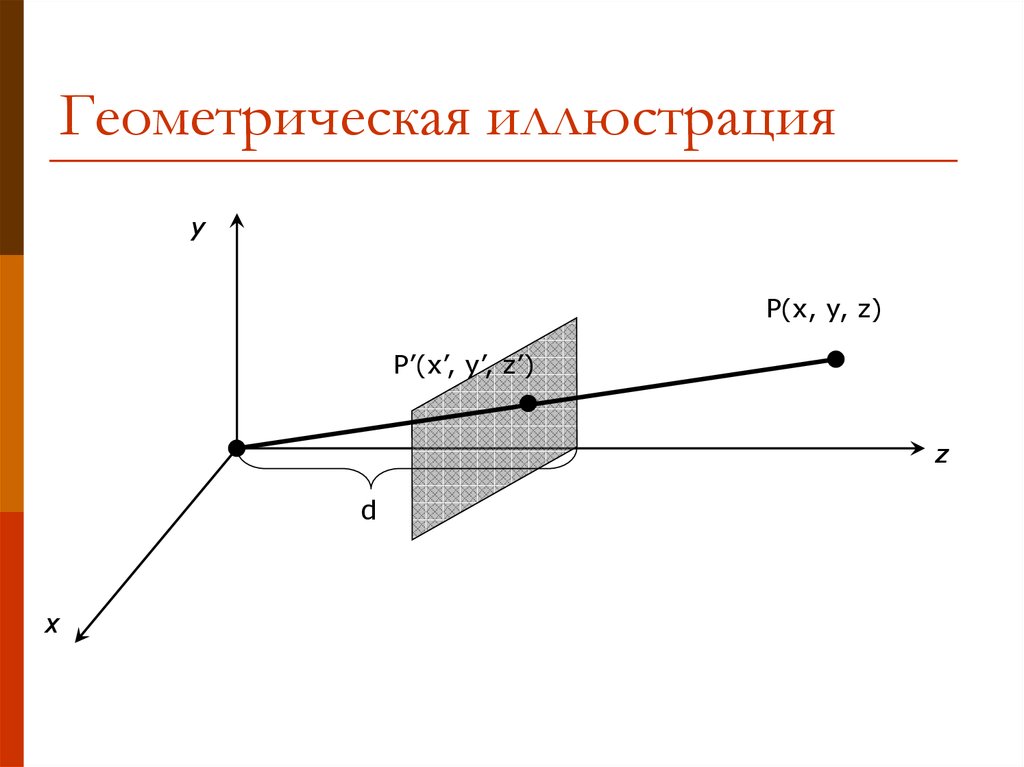
13. Геометрическая иллюстрация
yP(x, y, z)
P’(x’, y’, z’)
z
d
x
14. Вывод для первого варианта (r=1/d)
z=dВывод для первого варианта (r=1/d)
Из подобия треуг-ов:
x x
d z
d x
x
x
z
zd
P’(x’, y’, d)
x
x’
z
x
d
z
z=d
y
y y
d
z
P (x, y, z)
d y
y
y
z
z d
P (x, y, z)
P’(x’, y’, d)
y
y’
z
d
z
15. Проверка
10
( x, y , z,1)
0
0
0
1 0 0
z
( x, y , z , )
0 1 1d
d
0 0 0
0 0
x
y
x
y
(
,
, d ,1) (
,
, d ,1)
zd zd
r z r z
16. Получение перспективной проекции (2-й вариант)
КП Z = 0. Центр проекции лежит на осиz в точке (0, 0, -d)
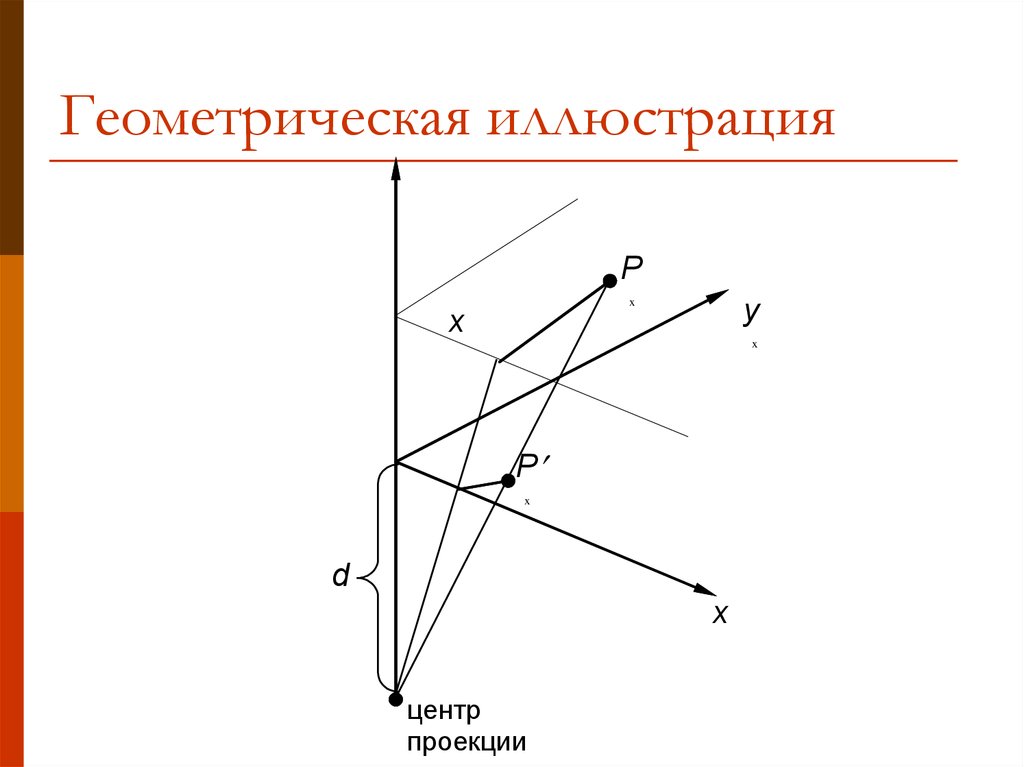
17. Геометрическая иллюстрация
Py
x
x
x
P
x
d
x
центр
проекции
18. Двухточечная угловая перспектива
Для получения двухточечной перспективы вобщей матрице преобразования устанавливают
коэффициенты p и q:
1
0
(x', y', z', 1) = (x, y, z, 1)
0
0
(x', y', z', 1) =
0 0
1 0
0 0
0 0
p
q
= [x, y, 0, (px+qu+1)];
0
1
x
y
,
,0,1
px qy 1 px qy 1
Такое преобразование приводит к двум точкам
схода. Одна расположена на оси X в точке (1/p, 0, 0,
1), другая на оси Y в точке (0, 1/q, 0 ,1)
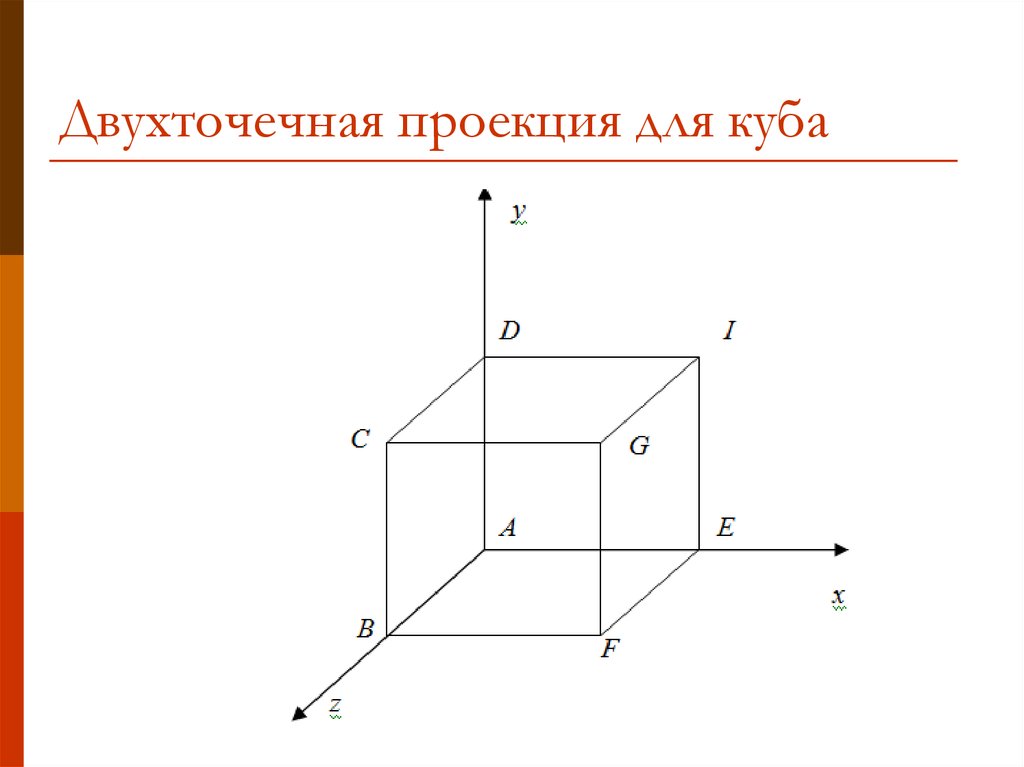
19. Двухточечная проекция для куба
20. Двухточечная проекция для куба (2)
A 0B 0
C 0
D 0
E 1
F 1
G 1
I 1
0 0 1
0 1 1
1 1 1 1
1 0 1 0
0 0 1 0
0 1 1 0
1 1 1
1 0 1
0 0
1 0
0 0
0 0
0
0
0,1 0
0,1 0
1
0
1 1
1
1
0 0
0 0
1 0
1 0
0 0
0 0
1 0
1 0
1 0
1 0
1,1 0
1,1 0
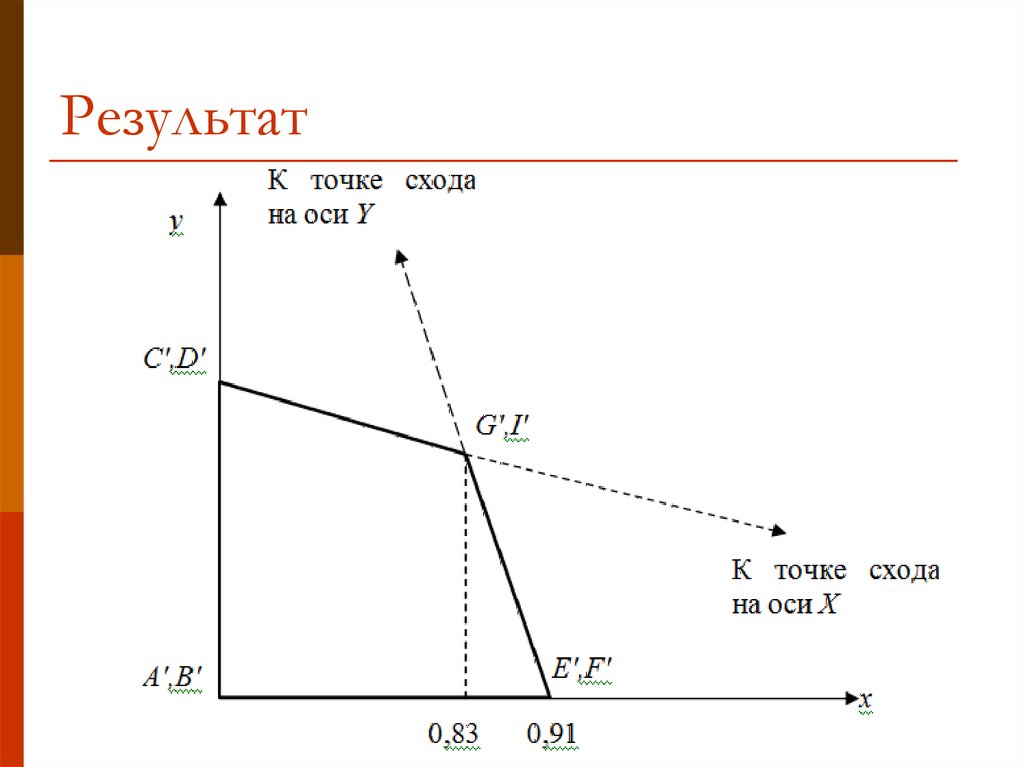
0,91
1,1
1,1 0,91
1,2 0,83
1,2 0,83
0
0
0,91
0,91
0
0
0,83
0,83
0 1 A'
0 1 B'
0 1 C '
0 1 D'
0 1 E '
0 1 F '
0 1 G '
0 1 I '
21. Результат
22. Трехточечная (косая) перспектива
10
0
0
p
1 0 q
0 1 r
0 0 1
0 0
23. Получение косоугольных проекций
10
Мкос=
l cos
0
0
1
l sin
0
0 0
0 0
0 0
0 1

















 Инженерная графика
Инженерная графика