Развертки поверхностей

1.

РАЗВЕРТКИ
ПОВЕРХНОСТЕЙ

2.

Тентовые сооружения
http://www.verteco.ru/projects/?tag=1&val=2008
http://www.prodayslona.ru/catalog/adds/element/82871/
http://www.breezair.ucoz.ru/photo/1-0-114-3
http://www.vip-express.ru/gallery/angar_galery.html

3.

Резервуары
воздуховоды
шаровый
http://www.ua.allbiz.info/buy/goods/?group=1000551&cid=210891
каплевидный
http://www.ua.allbiz.info/regions/index.php?fuseaction=adm_en
terprises.catalogProducts&rgn_id=14&cs=50&
page=3
http://www.tctena.ru/catalog.php?comp_id=10

4.

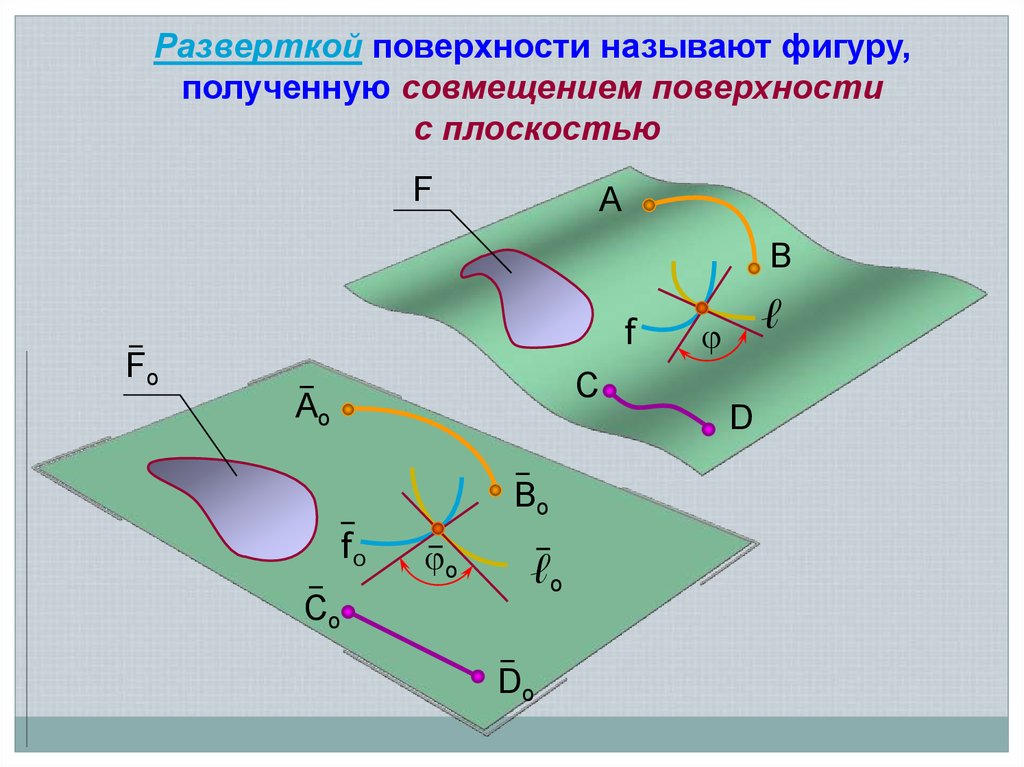
Разверткой поверхности называют фигуру,
полученную совмещением поверхности
с плоскостью
F
A
B
f
Fо
ℓ
C
Ao
D
Bo
fo
Co
о
ℓo
Do

5.

Основные свойства разверток
1. Длины линий на поверхности и на развертке
одинаковы
2. Углы между обыкновенными линиями
на поверхности равны соответствующим
углам на развертке
Углом между линиями называют угол,
образованный их касательными,
проведенными в точке пересечения линий
Преобразование, в котором сохраняется
равенство углов называется конформным
Поэтому поверхность и развертка конформны

6.

3. Прямые, параллельные на поверхности,
остаются параллельными и на развертке
Это вытекает из второго свойства
4. Площади, ограниченные замкнутой линией
на поверхности и на развертке равны
Преобразование, в котором сохраняется
равенство площадей, называют
эквиареальным

7.

5. Прямая линия на поверхности переходит
в прямую линию на развертке
6. Прямая линия между двумя точками на развертке
соответствует кратчайшему расстоянию между
этими точками на поверхности
Эти линии на поверхности называют
геодезическими линиями
Поверхности, для которых сохраняются
указанные свойства на развертке, называют
развертывающимися

8.

К числу развертывающихся
поверхностей относятся
многогранные поверхности;
из линейчатых –
цилиндрические, конические,
торсовые

9.

По возможностям и способам
построения различают развертки
точные, приближенные и условные
Точными называют развертки, построенные
с применением математического аппарата,
и развертки многогранных поверхностей
Приближенными – развертки, построенные
способом вписанных или описанных
многогранных поверхностей
Условные развертки неразвертывающихся
поверхностей строят способом цилиндров и конусов

10.

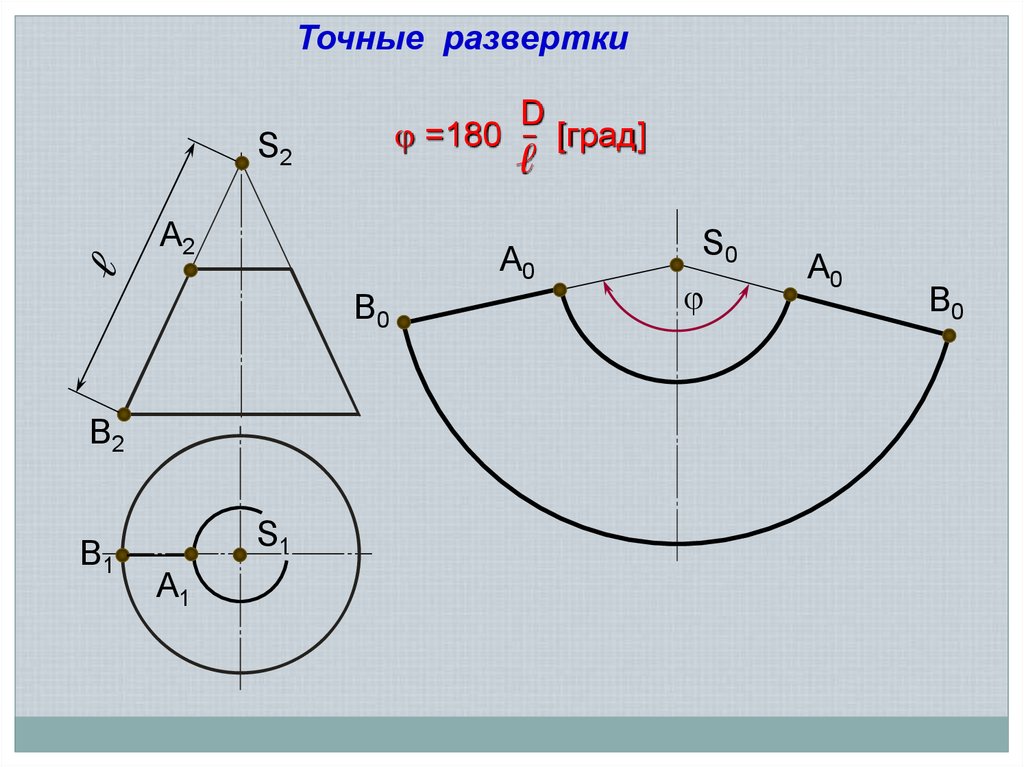
Точные развертки
D
=180 – [град]
ℓ
S2
A2
A0
B0
B2
B1
S1
A1
S0
A0
B0

11.

Развертка многогранных поверхностей
Способ нормального сечения
используется для построения разверток призм, боковые ребра
которых являются линиями уровня
15
G I2
12 FI2
22
35
0
10
G I0
30
10
20
K0
x
z
G0
G I1
K1
F1
F I0
KI2
F2 K2
G1
KI0
GI
32
11
G I0
<
2
G2
25
F0
G0
KI1
31
21
G0
F I1

12.

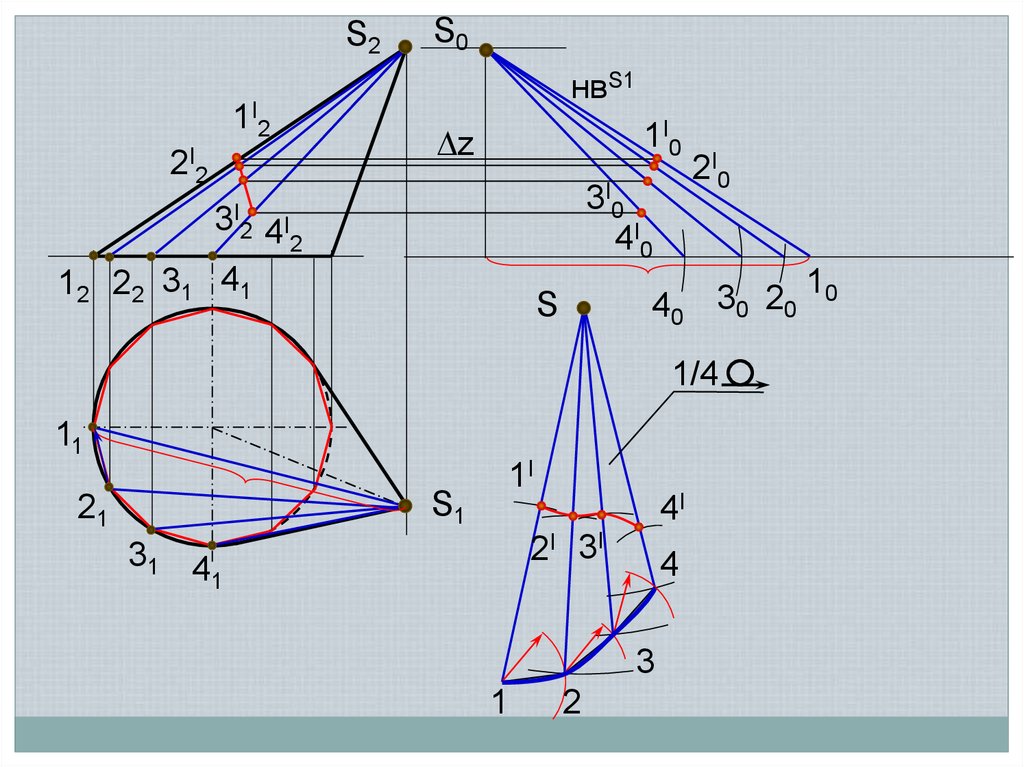
Приближенные развертки
Способ треугольников
(триангуляции)
Сущность способа заключается в том, что
кривую линейчатую поверхность заменяют
вписанной в нее многогранной
поверхностью с треугольными гранями,
нахождению натурального вида
многогранной поверхности
и последовательному построению
на чертеже

13.

S2
1I2
2I2
3I
2
S0
нвS1
1I0
z
3I0
4I0
4I2
12 22 31 41
S
40
2I0
30 20 10
1/4
11
S1
21
1I
4I
2I 3I
31 4
1
4
3
1
2

14.

Условная развертка на основе
аппроксимации
цилиндрическими или
коническими поверхностями

15.

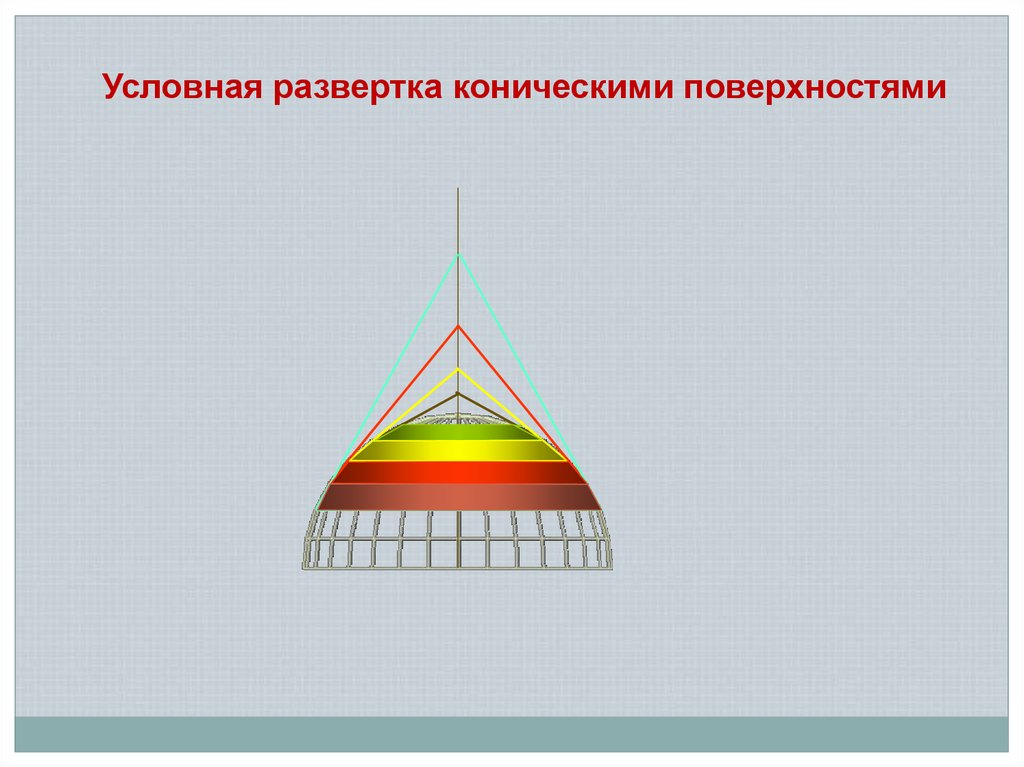
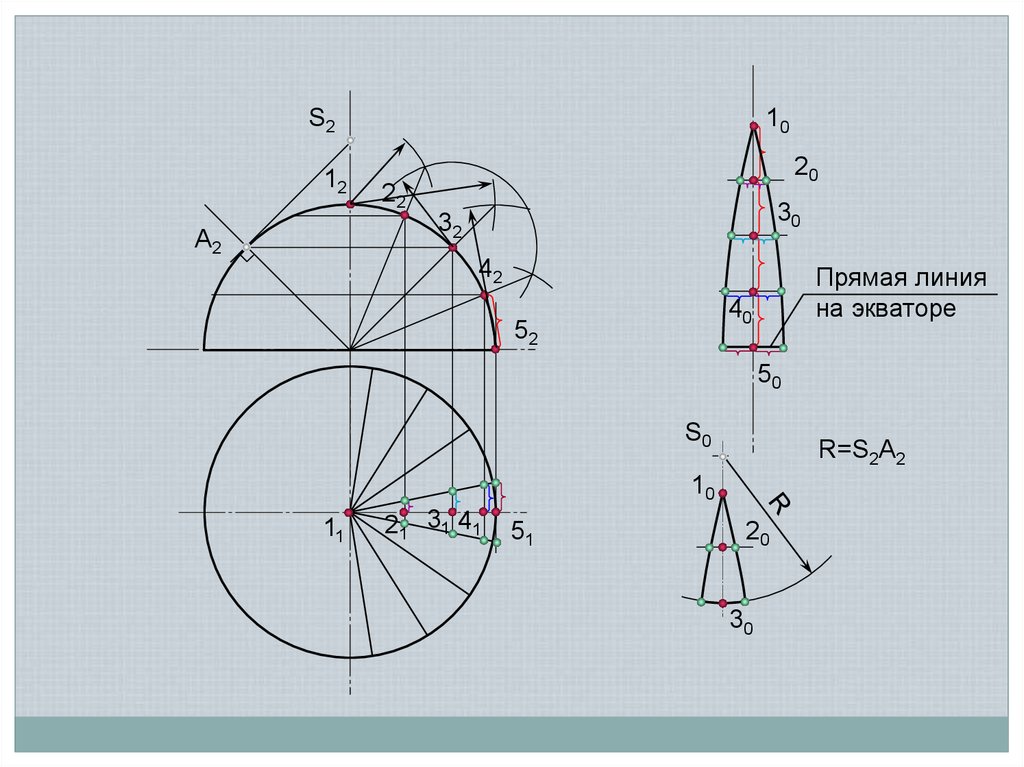
Условная развертка коническими поверхностями

16.

Условная развертка цилиндрическими поверхностями

17.

S2
12
10
20
22
30
32
A2
42
Прямая линия
на экваторе
40
52
50
S0
R=S2A2
10
11
21 31 41
51
20
30