Похожие презентации:
Электрические цепи в режиме постоянного тока и гармонических воздействий
1. Электрические цепи в режиме постоянного тока и гармонических воздействий
1. Электрические цепи врежиме постоянного тока
и гармонических
воздействий
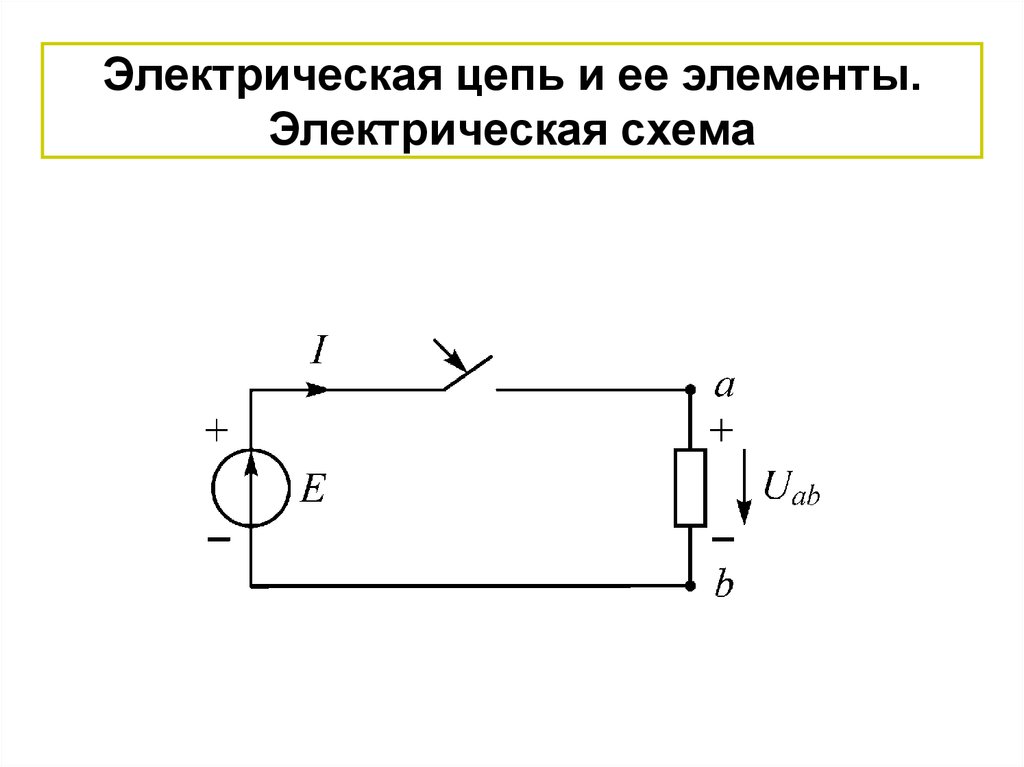
2. Электрическая цепь и ее элементы. Электрическая схема
3.
ЭДС E [B].Ток I [A].
Электрический ток – упорядоченное движение
зарядов под действием электрического поля.
U ab U a U b [В].
Напряжение – энергия, необходимая для перемещения единицы заряда из одной точки в другую.
4.
Независимые источники электрическойэнергии
Идеальный источник напряжения
Rг 0
Uг E
ВАХ
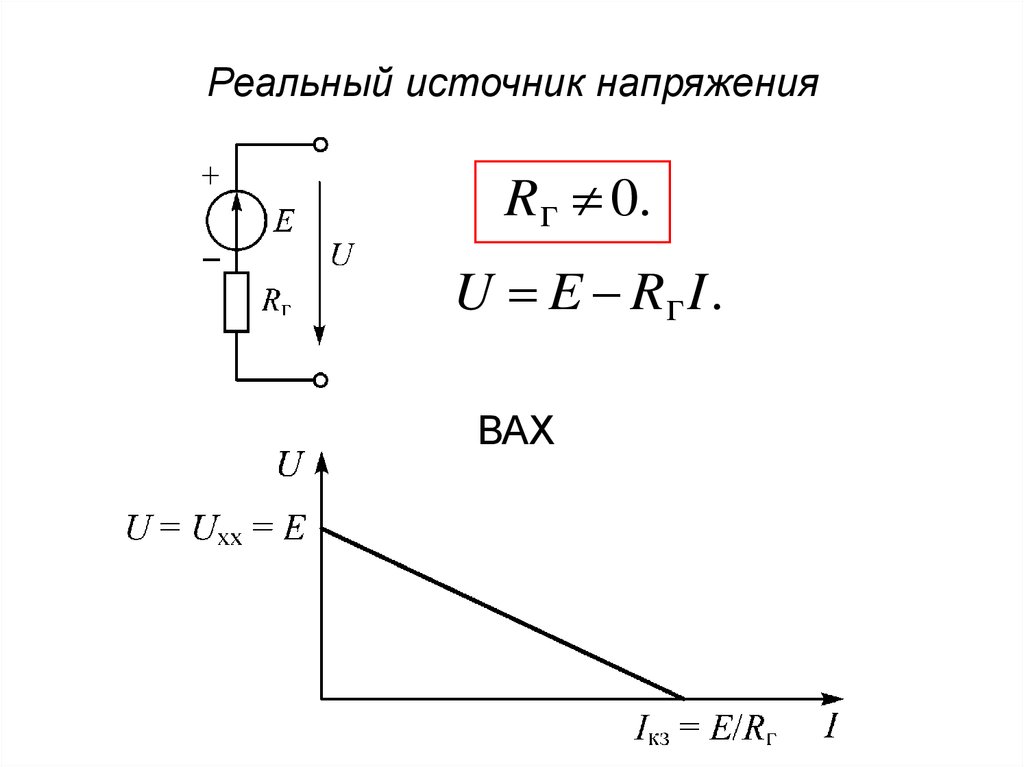
5.
Реальный источник напряженияRг 0.
U E Rг I .
ВАХ
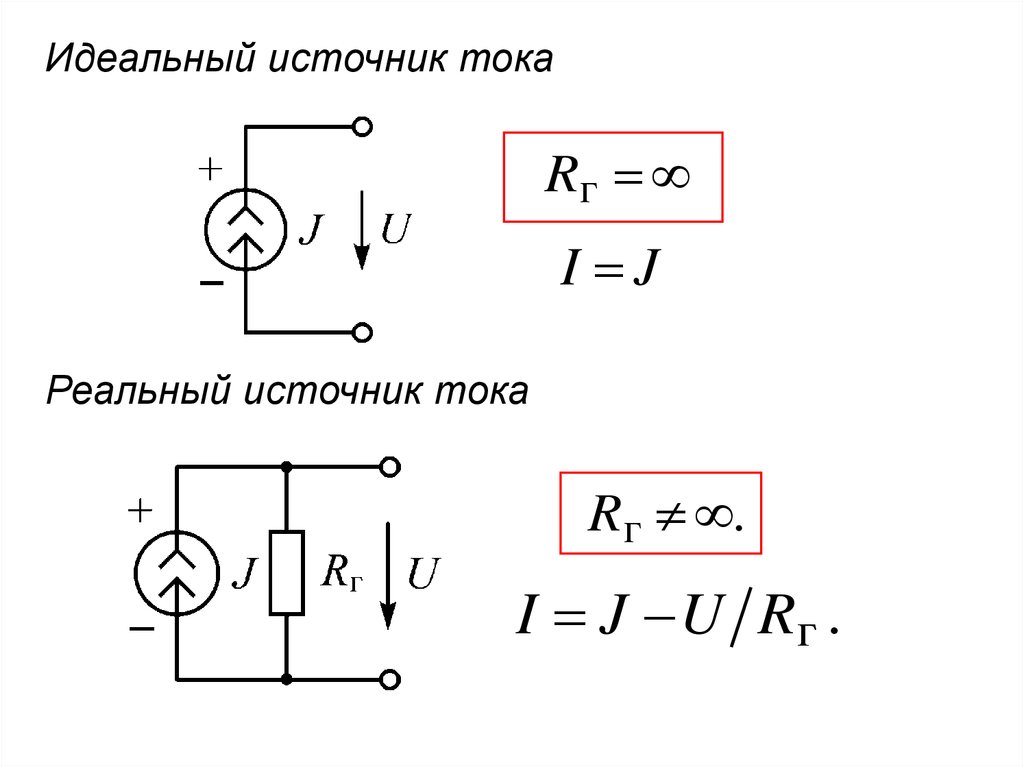
6.
Идеальный источник токаRг
I J
Реальный источник тока
Rг .
I J U Rг .
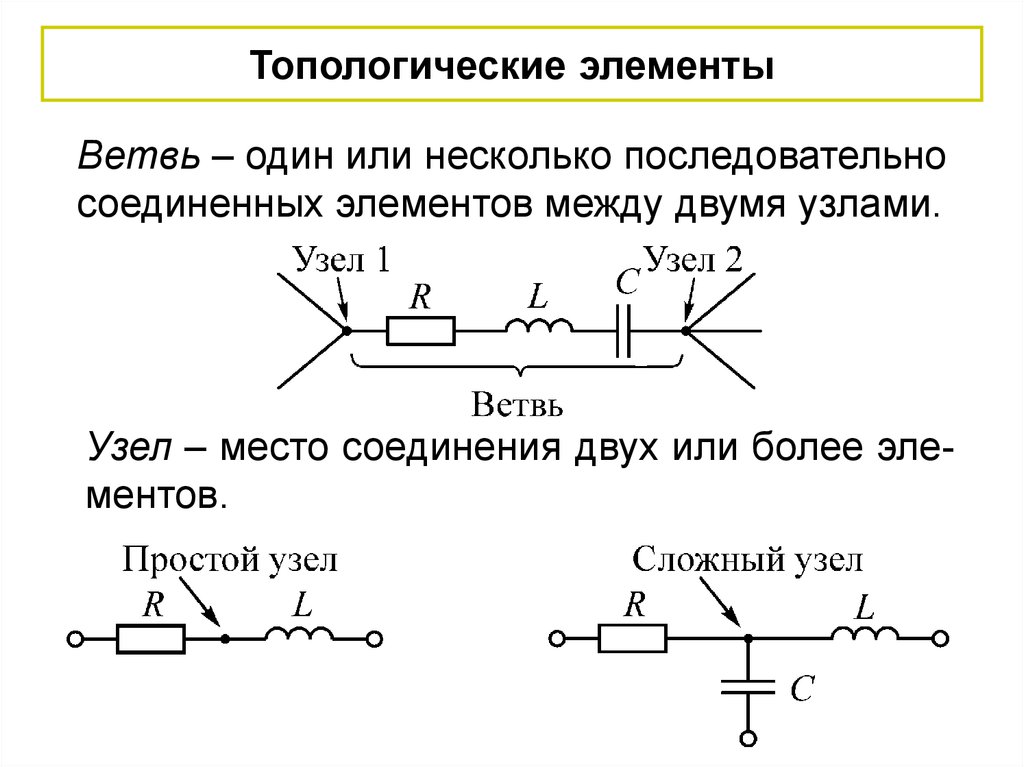
7.
Топологические элементыВетвь – один или несколько последовательно
соединенных элементов между двумя узлами.
Узел – место соединения двух или более элементов.
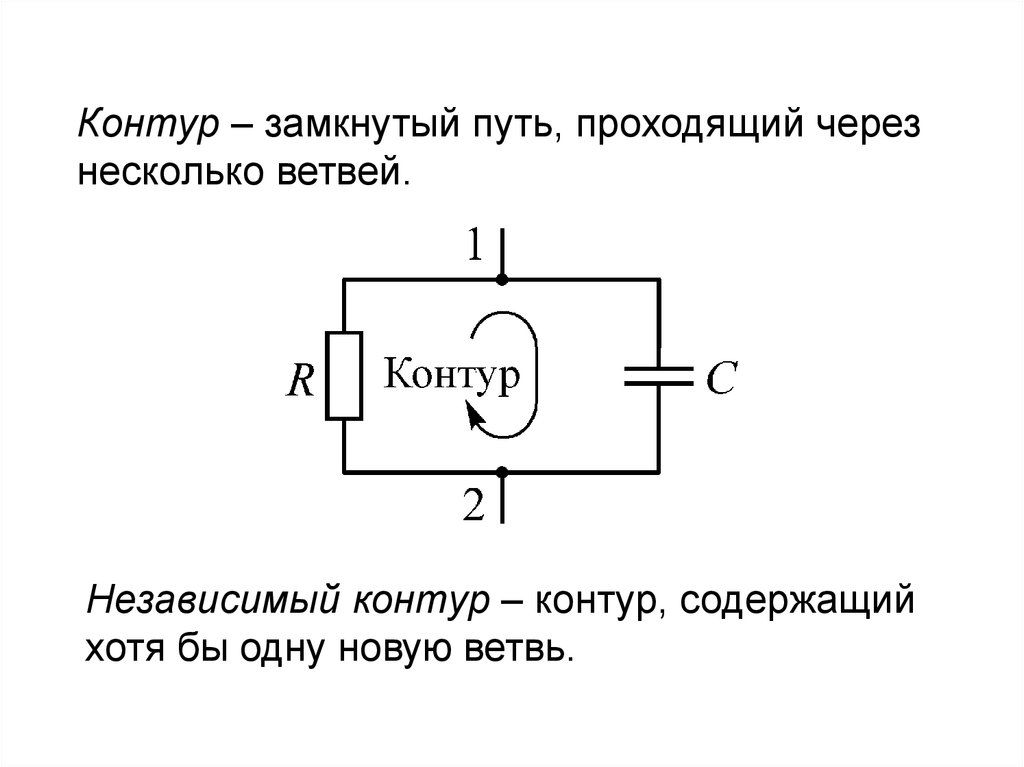
8.
Контур – замкнутый путь, проходящий черезнесколько ветвей.
Независимый контур – контур, содержащий
хотя бы одну новую ветвь.
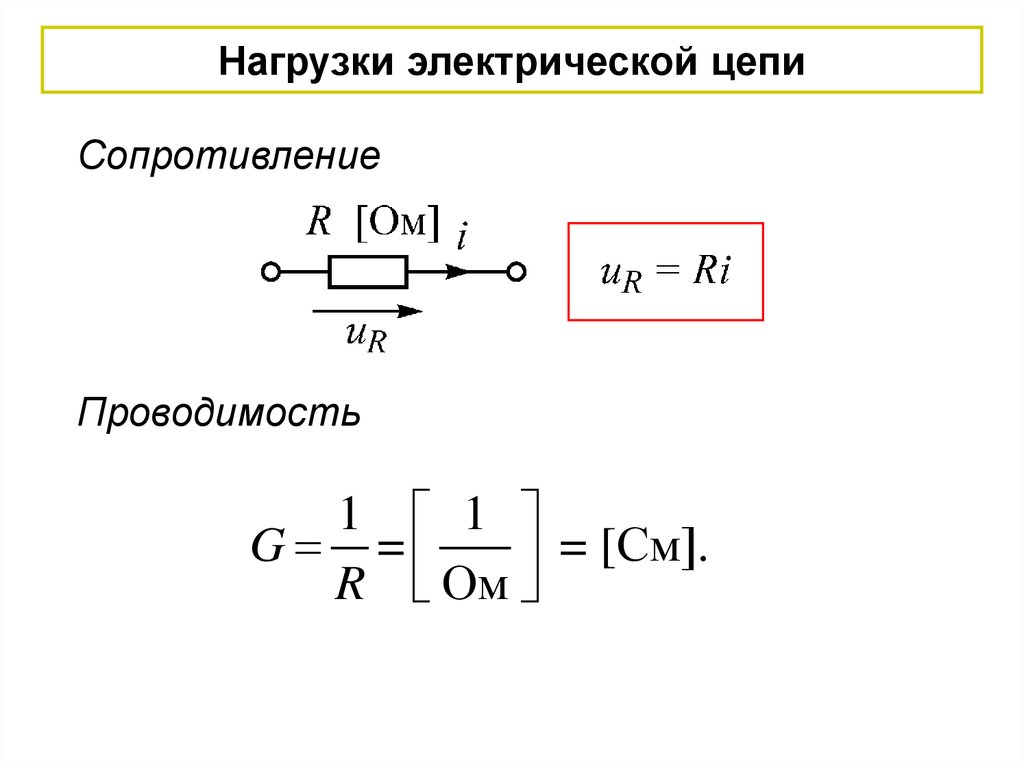
9.
Нагрузки электрической цепиСопротивление
Проводимость
1 1
G =
=
[См].
R Ом
10.
Индуктивный элементЕмкостной элемент
11.
Способы соединения нагрузока) Последовательное соединение элементов
R экв R1 R 2
n
R n Ri .
U 12
I
.
Rэкв
i 1
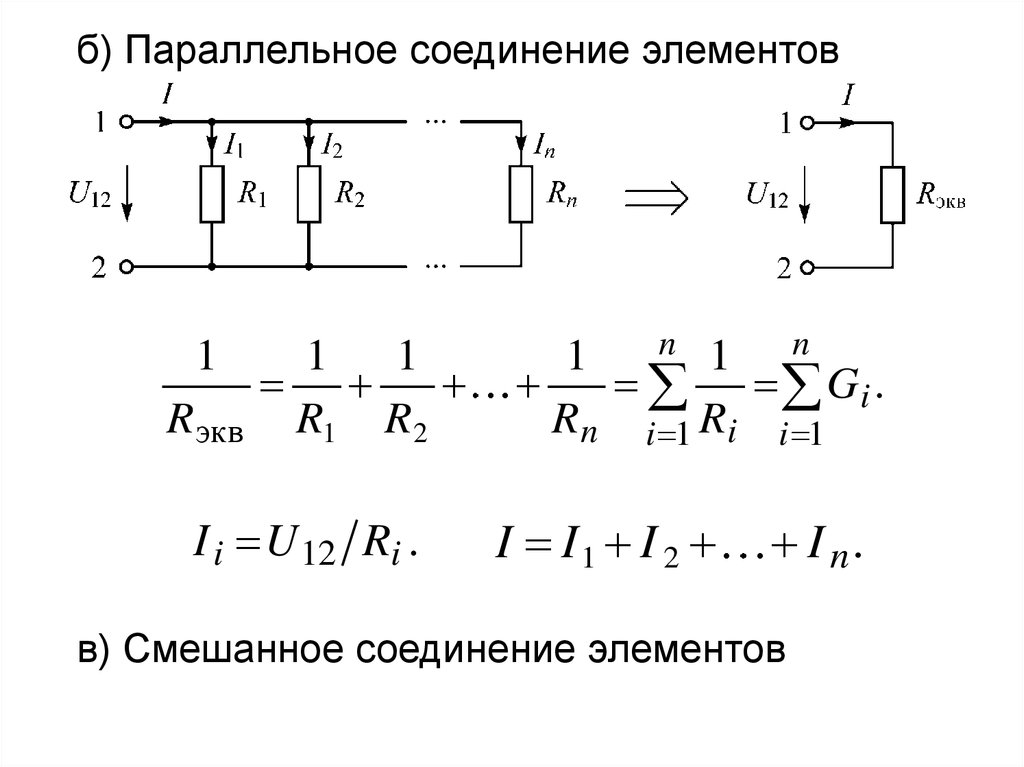
12.
б) Параллельное соединение элементов1
R экв
1
1
R1 R 2
I i U 12 Ri .
n 1
n
1
Gi .
R n i 1 Ri i 1
I I1 I 2
I n.
в) Смешанное соединение элементов
13.
Способы представления гармоническихколебаний
1. Временное представление
u t u U m sin t u
i t i I m sin t i
u t , i t – мгновенные или текущие значения
гармонического напряжения и тока;
U m , I m – амплитуды (максимальные значения
переменного напряжения и тока);
t u , t i – текущие фазы напряжения
и тока;
14.
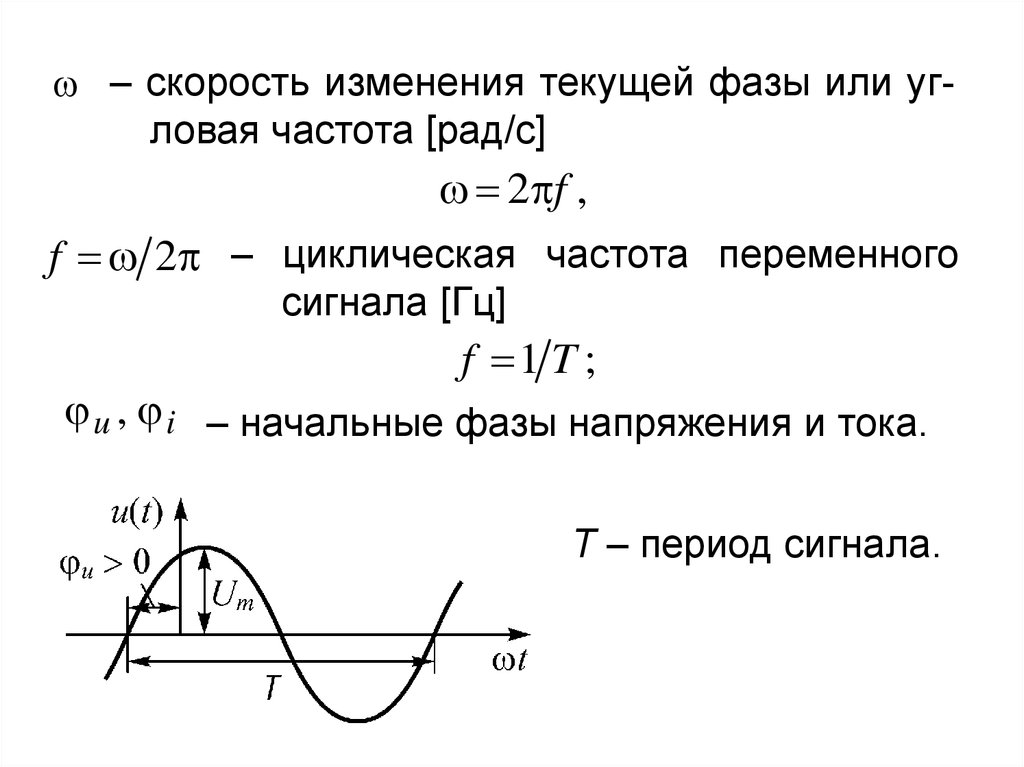
– скорость изменения текущей фазы или угловая частота [рад/с]2 f ,
f 2 – циклическая частота переменного
сигнала [Гц]
f 1 T ;
u , i – начальные фазы напряжения и тока.
Т – период сигнала.
15.
2. Векторное (классическое) представление3. Символическое (комплексное) представление
1 j
j 1
2
16.
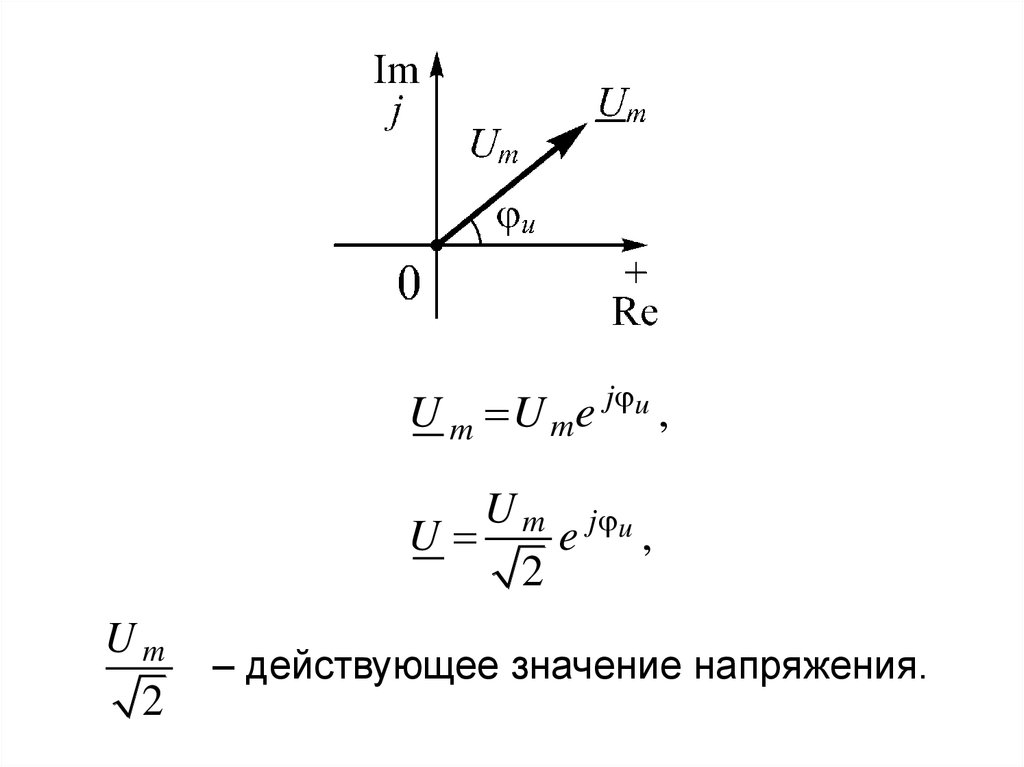
U m U mej u
,
U m j u
U
e ,
2
Um
2
– действующее значение напряжения.
17.
Символический метод расчетаU Ue j u ,
Z R R,
I Ie j i ,
U R I Z R,
Z L jX L j L,
1
1
Z C jX C j
,
C j C
U L I Z L,
U C I Z C ,
Z R , Z L , Z C – комплексные сопротивления резистора, индуктивности и емкости.
1
– реактивные сопротивлеX L L, X C
C
ния индуктивности и
емкости.
18.
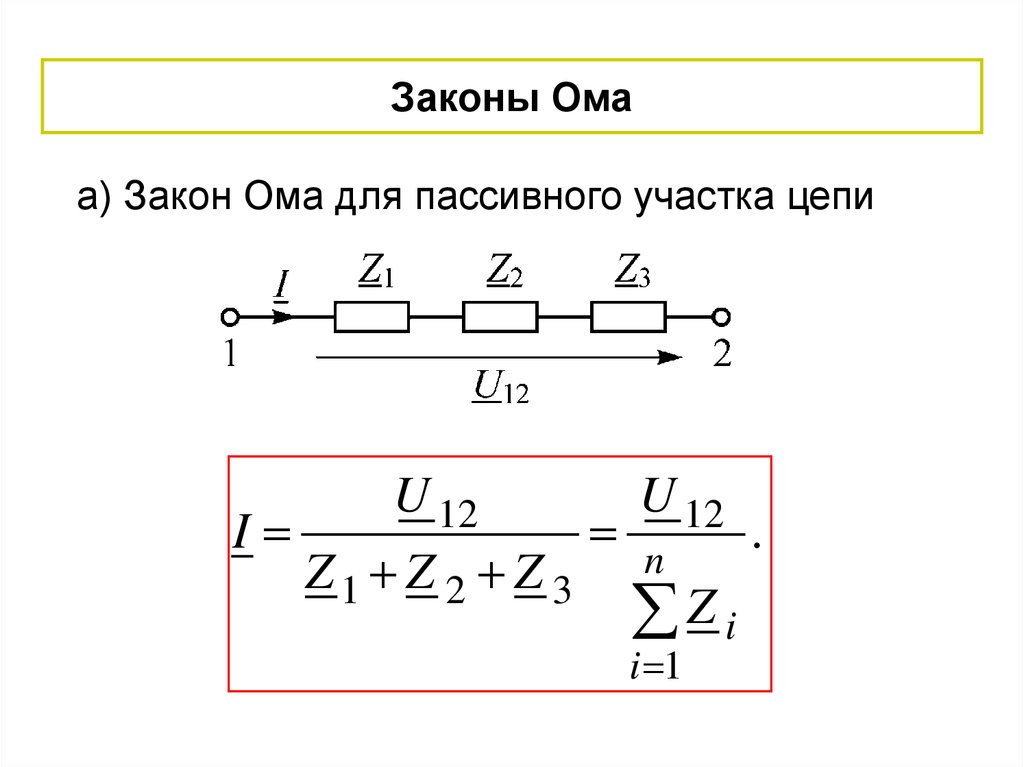
Законы Омаа) Закон Ома для пассивного участка цепи
U 12
U 12
I
n
.
Z1 Z 2 Z 3
Zi
i 1
19.
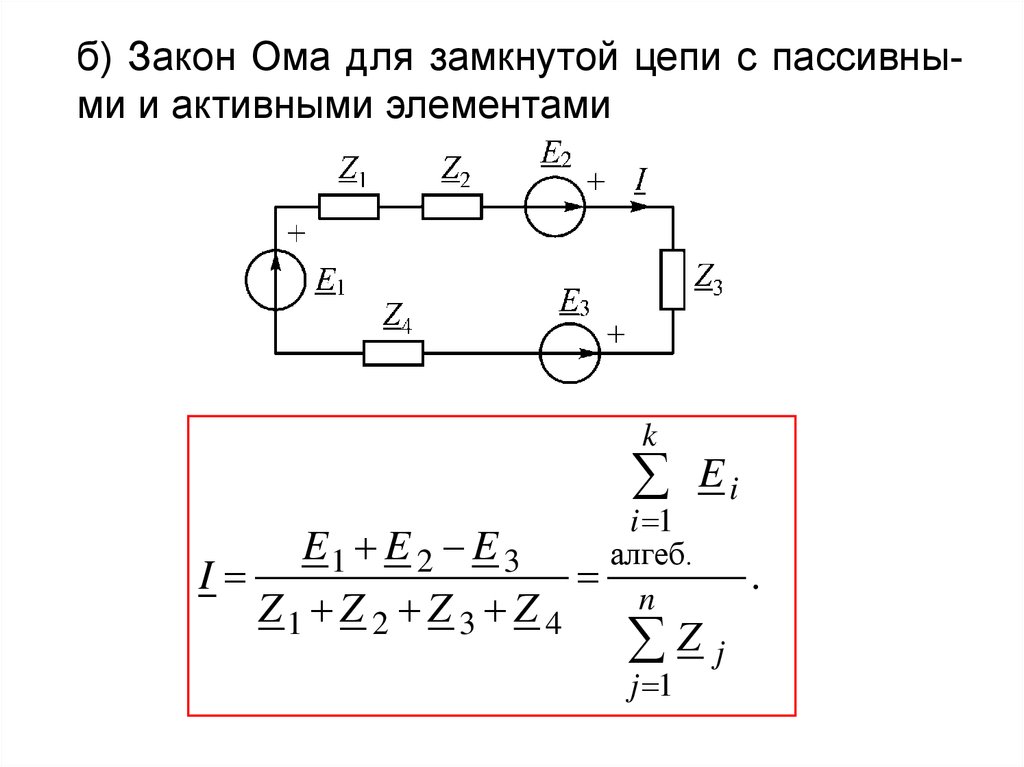
б) Закон Ома для замкнутой цепи с пассивными и активными элементамиk
E1 E 2 E 3
I
Z1 Z 2 Z 3 Z 4
i 1
алгеб.
n
Ei
Z j
j 1
.
20.
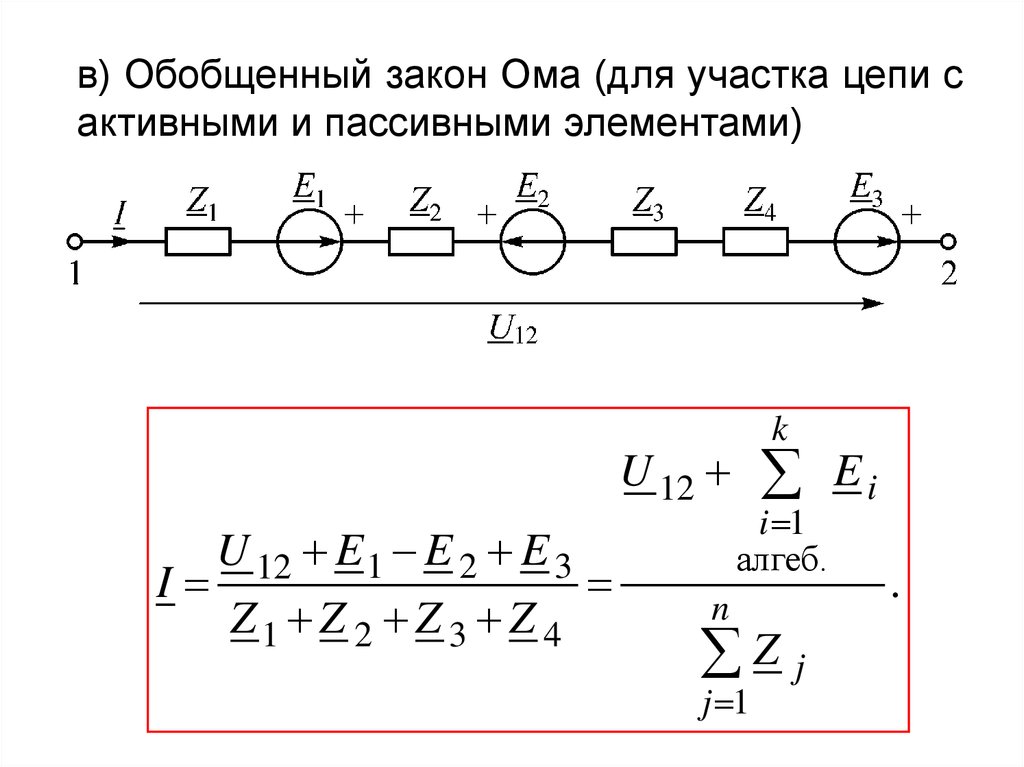
в) Обобщенный закон Ома (для участка цепи сактивными и пассивными элементами)
U 12
U 12 E 1 E 2 E 3
I
Z1 Z 2 Z 3 Z 4
k
i 1
алгеб.
n
Z j
j 1
Ei
.
21.
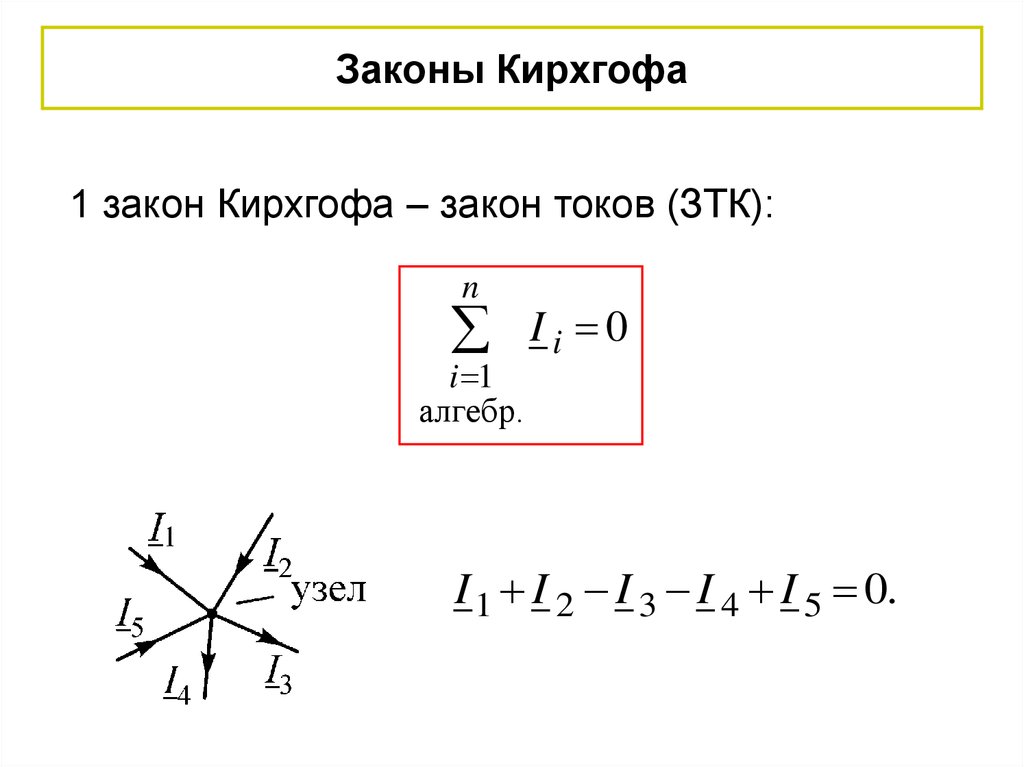
Законы Кирхгофа1 закон Кирхгофа – закон токов (ЗТК):
n
i 1
алгебр.
Ii 0
I 1 I 2 I 3 I 4 I 5 0.
22.
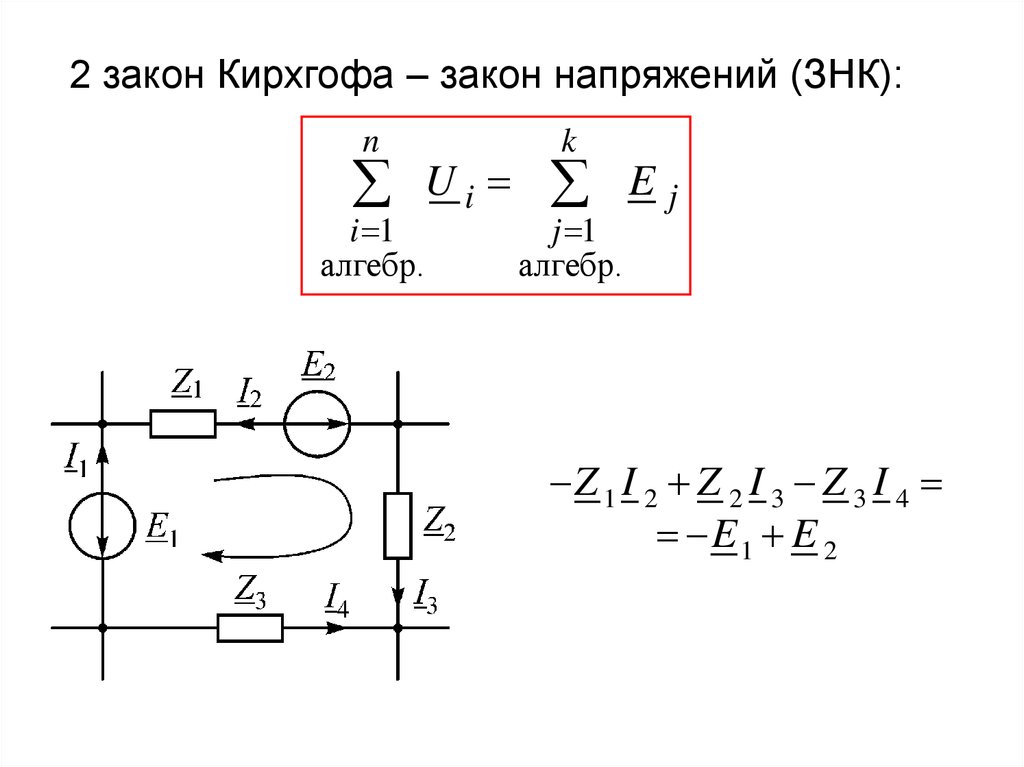
2 закон Кирхгофа – закон напряжений (ЗНК):n
Ui
i 1
алгебр.
k
j 1
алгебр.
E
j
Z 1 I 2 Z 2 I 3 Z 3 I 4
E 1 E 2
23.
Методы расчета цепей постоянного ипеременного тока
1. Метод свертывания.
2. Метод законов Кирхгофа.
3. Метод наложения.
4. Метод контурных токов.
5. Метод узловых напряжений.
6. Метод эквивалентного генератора.
24.
Мощность в цепи переменного тока. Балансмощностей
1. Мощность источника
Комплексная мощность
S E I * S cos S jS sin S PE jQ E ,
где P – активная мощность источника [Вт],
Q – реактивная мощность источника [ВАР],
S – полная мощность источника [ВА].
25.
2. Мощность нагрузока) Резистор
S R U I * I 2 R U 2 R P [Вт].
б) Индуктивность
S L U I * jI 2 X L jQ L ВАР .
QL
в) Конденсатор
SC
2
*
U I jI X
QC
C
jQC ВАР .
26.
Баланс мощностиS ист S нагр
Pист jQист Pнагр jQнагр
Pист Pнагр ; Qист Qнагр .
27.
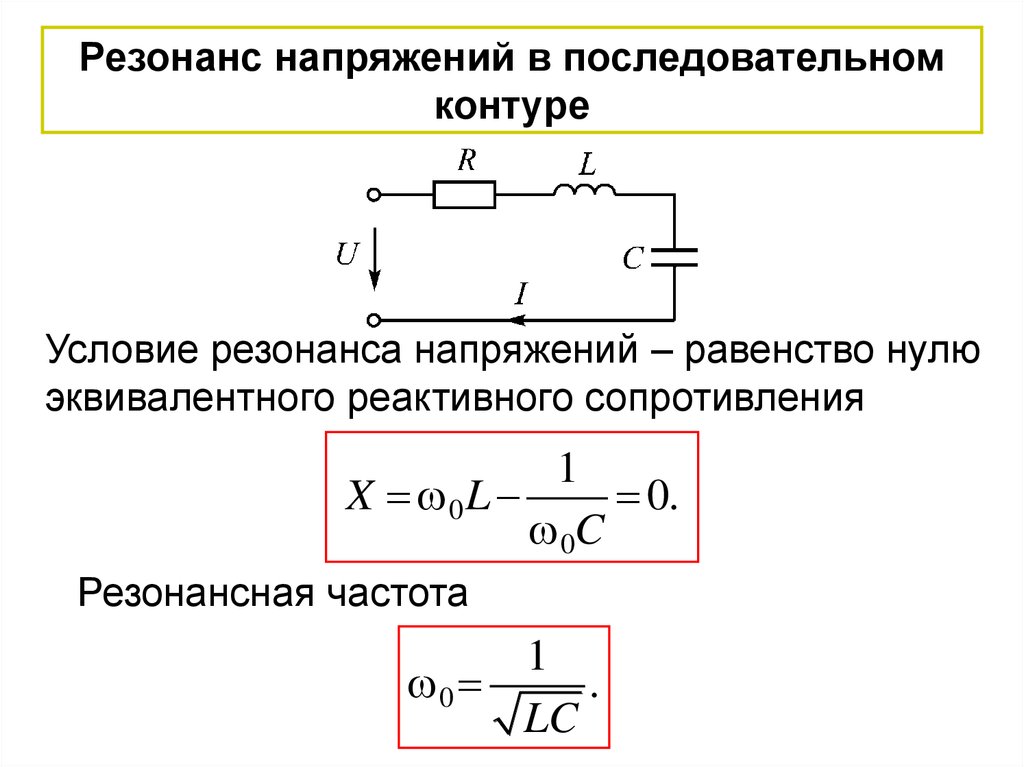
Резонанс напряжений в последовательномконтуре
Условие резонанса напряжений – равенство нулю
эквивалентного реактивного сопротивления
1
X 0 L
0.
0C
Резонансная частота
1
0
.
LC
28.
LC
– характеристическое сопротивление.
При резонансе Z = R, ток
I I 0 U R.
U L 0 U C 0 QU ,
где Q
U L0 U C 0
– добротность контура.
R U
U
29.
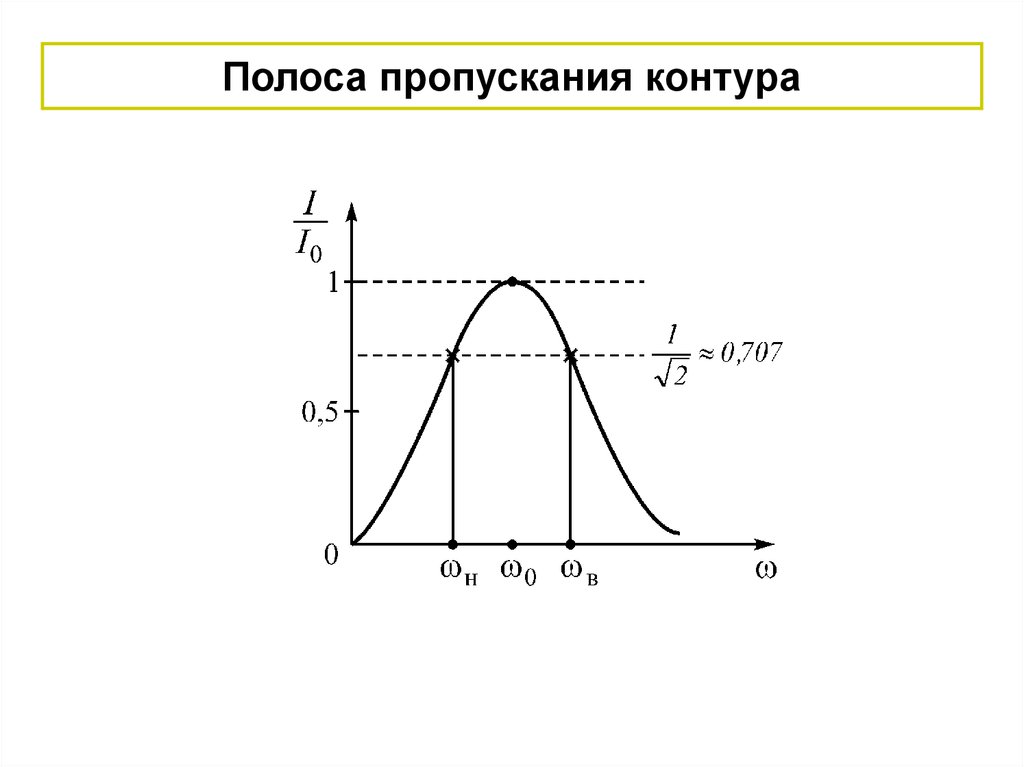
Полоса пропускания контура30.
Абсолютная полоса пропускания:0 рад
S A в н
Q с
или
f0
S A f в f н 2 f
Q
Гц ,
где f = fв – f0 = f0 – fн – абсолютная расстройка
контура.
31.
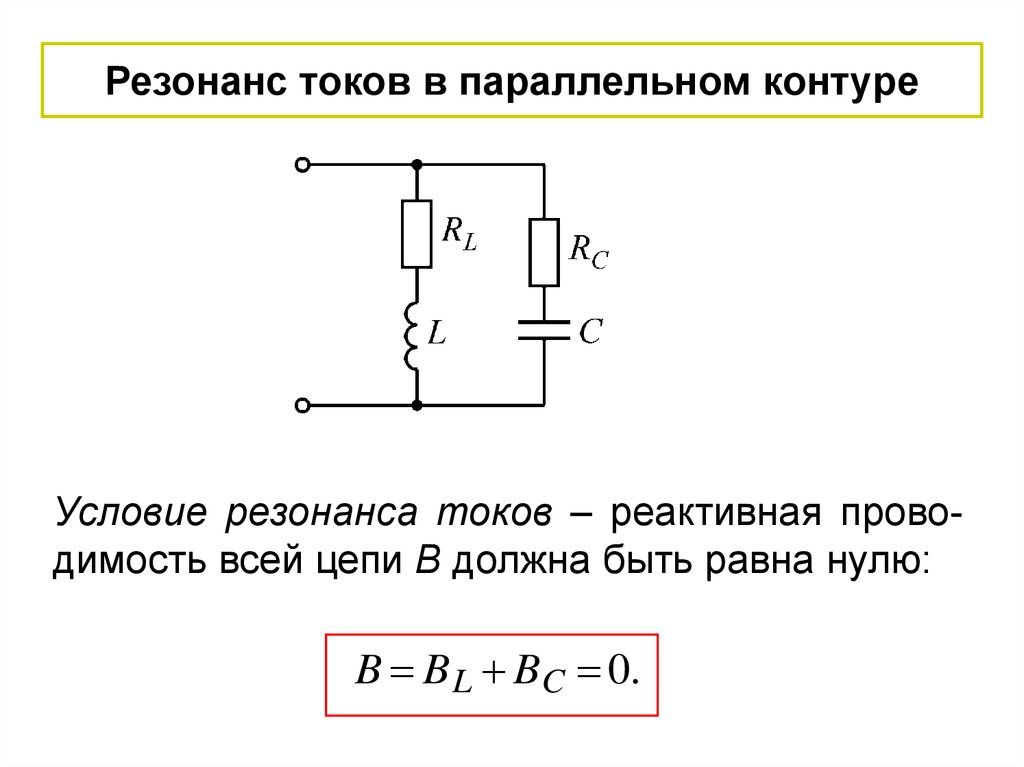
Резонанс токов в параллельном контуреУсловие резонанса токов – реактивная проводимость всей цепи В должна быть равна нулю:
B B L BC 0.
32.
Резонансная частота1
p
LC
где
2 R L2
2 RC2
0
2 R L2
2 RC2
,
L C.
Для высокодобротного контура, у которого
Q RL RC 1
и
RC 0, R L R
1
p 0
LC
33.
Нормированная частотная характеристика напряжения34. 2. Линейные электрические цепи в режиме негармонических воздействий
35.
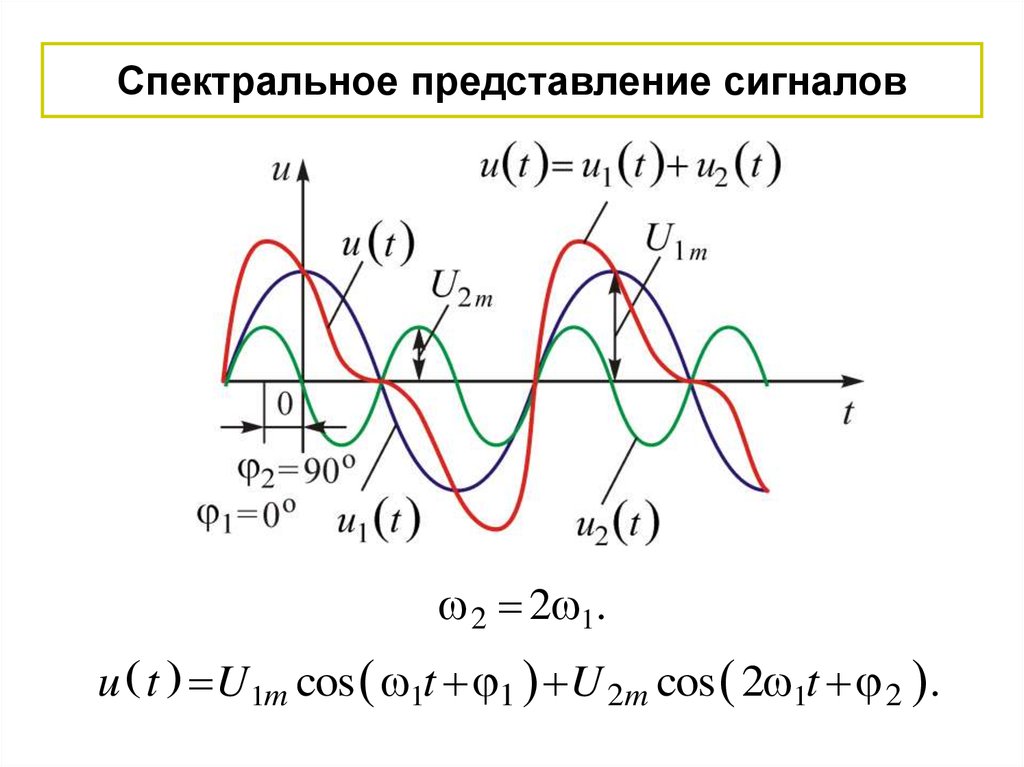
Спектральное представление сигналов2 2 1.
u t U 1m cos 1t 1 U 2m cos 2 1t 2 .
36.
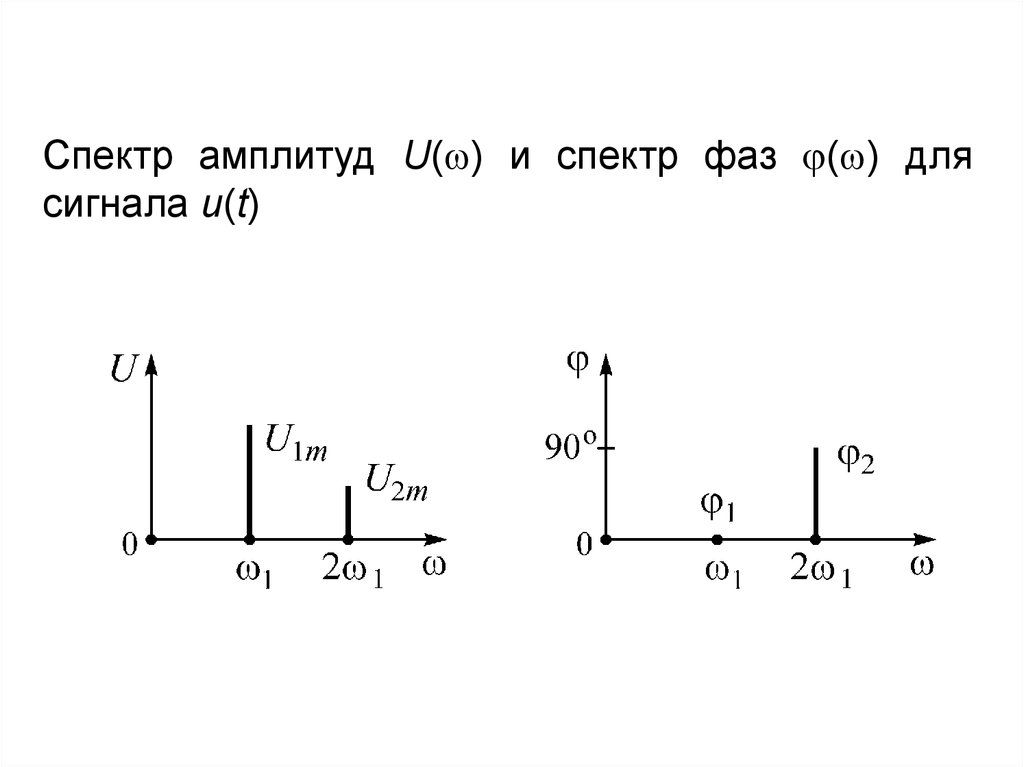
Спектр амплитуд U( ) и спектр фаз ( ) длясигнала u(t)
37. Спектры периодических сигналов
1. Тригонометрическая форма ряда Фурьеа)
a
u t 0 a k cos k 1t bk sin k 1t ,
2 k 1
a 0 1 T – постоянная составляющая;
A0 u t dt
2 T0
Ak
2
2
a k bk
– амплитуда k-ой гармоники;
bk
– фаза k-ой гармоники.
k arctg
ak
38.
б)u t A0 Ak cos k 1t k .
k 1
2. Комплексная форма ряда Фурье
1
u t A k e jk 1t .
2 k
Анализ спектрального (гармонического) состава
периодических сигналов – это вычисление
амплитуд Umk и начальных фаз k гармонических
составляющих ряда Фурье.
39. Спектры непериодического сигнала
Прямое преобразование ФурьеU j
u t e j t dt.
позволяет определить спектральную плотность
сигнала.
U(j ) – комплексная спектральная плотность.
U j U j e
j
,
|U(j )| – спектральная плотность амплитуд,
( ) – спектральная плотность фаз.
40.
Обратное преобразование Фурье1
j t
u t
U
j
e
d .
2
позволяет определить сигнал по его спектральной плотности.
41. Законы коммутации
Переходные процессы в линейныхэлектрических цепях
Законы коммутации
1-ый закон коммутации
i L 0 i L 0 .
2-ой закон коммутации
u C 0 u C 0 .
42. Классический метод анализа переходных процессов
– решение дифференциального уравнения относительно тока или напряжения в цепи.Для составления такого уравнения используются законы Кирхгофа.
Вид искомого решения:
u C (t ) u C пр u C св t u C пр Ae pt .
43. Преобразование Лапласа
Операторный метод анализа переходных процессов базируется на преобразованиях Лапласа.f t – оригинал функции
F p – изображение функции.
p j – комплексная переменная.
а) Прямое преобразование Лапласа
F p f t e pt dt.
0
44.
б) Обратное преобразование Лапласаj
1
pt
f t
F p e dp.
2 j j
Запись преобразования Лапласа
f t F p .
45. Законы Ома и Кирхгофа в операторной форме
ЗТК в операторной форме:I k p 0.
алг.
ЗНК в операторной форме:
U k p E n p .
алг.
алг.
46. Расчет переходных процессов операторным методом
Порядок расчета:1. Расставляются токи в ветвях.
2. Находятся: uC(0+) и iL(0+).
3. Составляется операторная схема замещения.
4. Определяются изображения токов в ветвях
или напряжений на элементах.
5. Переходят от изображений токов и напряжений к мгновенным значениям i(t), u(t).
47. Временные методы анализа переходных процессов
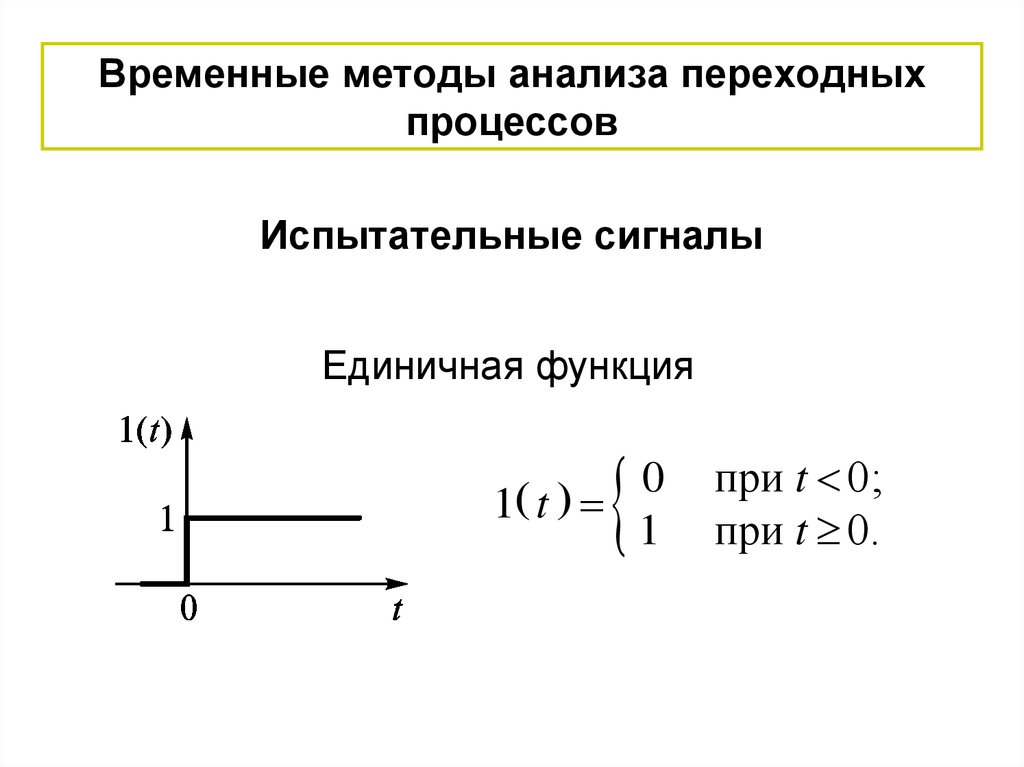
Испытательные сигналыЕдиничная функция
0
1 t
1
при t 0;
при t 0.
48.
Единичная импульсная функция ( -функция)0, при t 0,
t , при t 0,
0, при t 0.
t
d
1
t
.
dt
49.
Свойства -функции:1. Площадь единичной импульсной функции
равна единице
t dt 1.
2. Фильтрующее свойство
f t t t 0 dt f t 0 .
50. Переходная характеристика цепи
f реакц tg t
.
1 t
t
u
g u t
безрамерная .
1 t
t
i
См .
g y t
1 t
51. Импульсная характеристика цепи
h tf реакц t
S0
f реакц t
1
.
Связь между импульсной h(t) и переходной
g(t) характеристиками
t
dg
h t
g 0 t g t .
dt
52. Анализ реакции цепи с помощью интеграла Дюамеля
tu реакц t u возд 0 g t u возд g t d .
0
53.
Порядок расчета:1. Разбить сигнал на участки интегрирования,
найти скачки напряжения на границах участков,
найти производные сигнала на каждом из
участков.
2. Рассчитать переходную характеристику заданной цепи.
3. Записать интеграл Дюамеля для каждого из
участков интегрирования.
4. Построить график.
54. Анализ реакции цепи с помощью интеграла наложения
tf 2 t f 1 h t d .
0


































 Физика
Физика








