Дисперсионный и корреляционно-регрессионный анализ

1. Дисперсионный и корреляционно-регрессионный анализ

Дисперсионный и корреляционнорегрессионный анализ
Преподаватель Е. В. Луценко
Работа Чеснокова М.С.
группа №234

2. Вводная часть

• Цель
Сформулировать представления о
дисперсионном и корреляционнорегрессионном анализе
• Задачи
– Познакомиться с базовыми терминами статистики
– Узнать, что такое дисперсионный и
корреляционно-регрессионный анализ. Их
применение
– Рассмотреть конкретные примеры

3. Задание 1 Определение основных статистичес ких показаетлей, используя «Мастер функций»

48.56.54.57.47.50.59.60.67.68.70.69.74.75.53.58.86.
51.88.60.87.65.69.71.68.50.61.76.77.61.85.59.88.64.
51.86.91.78.52.49.81.55.62.63.73.72.72.66.80.79.82.
84.75.83.84.83.72.73.73.62.67.81.63.83.64.66.67.67.
66.68.71.76.63.66.64.66.65.68.76.78.77.68.72.73.74.
79.78.77.76.70.69.72.73.69.71

4. Результат

Значе
ние Смысл величины
Выборочное
среднее
Мода
69,42Это значение, которое является средним арифметическим
68Число, наиболее часто встречающееся в данном множестве чисел.
Число, которое является серединой множества чисел: половина чисел имеют
69 значения большие, чем медиана, а половина чисел — меньшие
Медиана
Минимально
е значение
47Возвращает наименьшее значение в списке аргументов.
Максимальн
ое значение
91Возвращает наибольшее значение из набора значений.
Объем
выборки
95Количество аргументов
Сумма
6595Сумма аргументов
106,5 Дисперсия показывает степень отклонения от среднего, т.е. показывает разброс
Дисперсия
868 аргументов
Среднее
квадратично 10,32 Стандартное отклонение — это мера того, насколько широко разбросаны точки
е отклонение 409 данных относительно их среднего.
Ошибка
средняя ошибка выборки показывает, какие возможны отклонения характеристик
выборочной 1,242 выборочной совокупности от соответствующих характеристик генеральной
средней
874 совокупности.
Возвращает доверительный интервал для среднего генеральной совокупности,
используя нормальное распределение.
Доверительн 2,076
ый интервал
051

5. Результат

Столбец1
Среднее
Стандарт
ная
ошибка
Медиана
Мода
Стандарт
ное
отклонен
ие
Дисперси
я
выборки
Эксцесс
Асиммет
ричность
Интервал
Миниму
м
Максиму
м
Сумма
Счет
69,42105
1,059229
69
68
10,32409
106,5868
-0,46761
-0,18255
44
47
91
6595
95

6. Задание 3 Построение полигоны и гистограммы, используя данные статистического исследования

Задание 3
Интервал
25
50
5
55
6
60
7
65
12
70
20
75
17
5
80
13
0
85
9
90
5
95
1
20
15
Частота
10
50
55
60
65
70
75
80
85
90
95

7. Задание 4. Определить достоверность различия средних арифметических двух выборок

Изначальные
данные
АД1
АД2
250
240
210
190
185
170
210
195
165
170
155
175
Парный двухвыборочный
t-тест для средних
Среднее
Дисперсия
Наблюдения
Корреляция
Пирсона
Гипотетическая
разность средних
df
t-статистика
Вывод:Отвергается
гипотеза об
отсутствии различий
в двух выборках
Переменная 1
Переменная 2
207,5
178,3333
1017,5
416,6667
6
6
0,813981
0
5
3,69343
P(T<=t)
одностороннее
0,007048
t критическое
одностороннее
2,015048
P(T<=t)
двухстороннее
0,014095
t критическое
двухстороннее
2,570582

8. Корреляционно-регрессионный анализ

9. Вычисление коэффициента корреляции

Изначальные данные
Вес щитовидной железы
Площади стенографического
изображения
12
59
62
95
102
23
203
270
122
41
11
32
33
44
46
17
73
89
52
25
С использованием
«Мастера функций»
С использованием
«Пакета анализа»
Строка 1 Строка 2
Коэффициент корреляции
Строка 1
1
Строка 2
0,992148
0,992148
1
Вывод о характере и тесноте связи между весом щитовидной железы
и соответствующей ей площади стенографического изображения по
вычисленному коэффициенту корреляции: Связь тесная
Т.к. 0.7< Коэф. Корр.<1

10. Выполнить регрессионный анализ Сделать прогноз при опрпеделенном значении аргумента

Регрессионный анализ с
использованием « Мастера
функций»:
Находим с помощью «Мастера
функций» коэфф. В : 503,4

11.

12.

13.

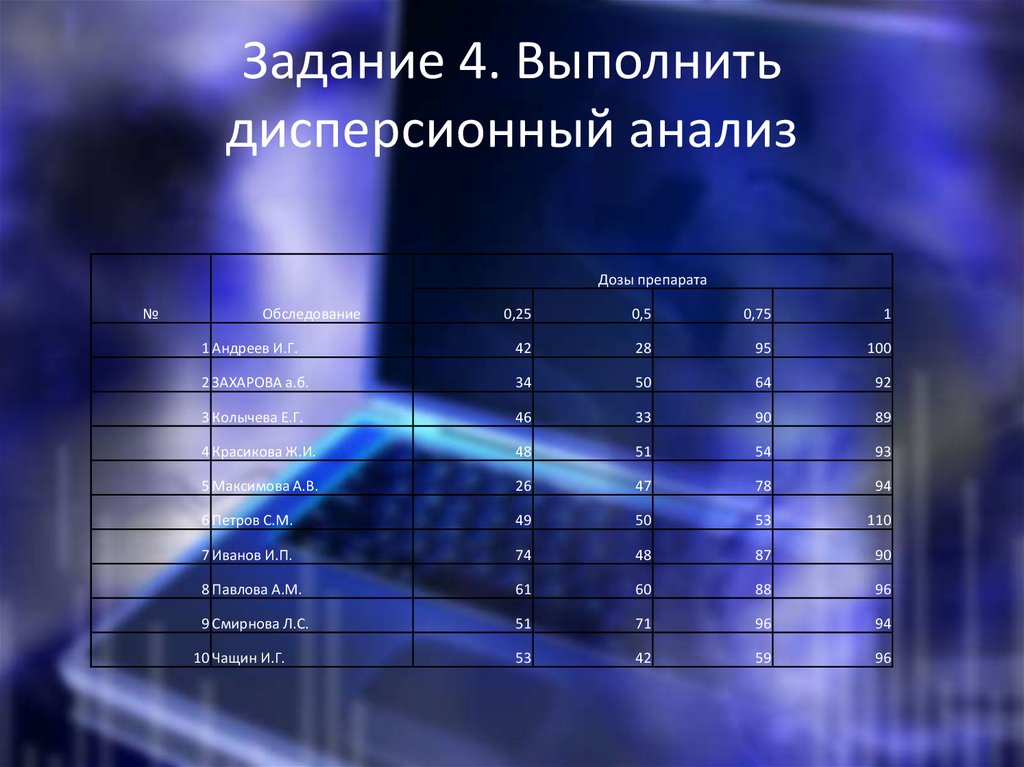
14. Задание 4. Выполнить дисперсионный анализ

Дозы препарата
№
Обследование
0,25
0,5
0,75
1
1 Андреев И.Г.
42
28
95
100
2 ЗАХАРОВА а.б.
34
50
64
92
3 Колычева Е.Г.
46
33
90
89
4 Красикова Ж.И.
48
51
54
93
5 Максимова А.В.
26
47
78
94
6 Петров С.М.
49
50
53
110
7 Иванов И.П.
74
48
87
90
8 Павлова А.М.
61
60
88
96
9 Смирнова Л.С.
51
71
96
94
53
42
59
96
10 Чащин И.Г.

15. Результаты анализа

Однофакторный
дисперсионный анализ
Группы
Столбец
1
Столбец
2
Столбец
3
Столбец
4
Счет
Дисперси
Среднее
я
Сумма
10
484
48,4
177,6
10
480
48 150,2222
10
764
76,4 296,7111
10
954
95,4 36,26667
Дисперсионный анализ
Источни
к
вариации
Между
группами
Внутри
групп
Итого
SS
df
16018,7
5947,2
MS
F
F
Pкритичес
Значение
кое
3 5339,567 32,32183 2,57E-10 2,866266
36
165,2
21965,9
39
F>Fкрит.
Вывод: Различия не обусловлены, значит, влияние лекарственного
препарата на длительность терапевтического эффекта случайны