Похожие презентации:
Задачи. Конвективный теплообмен
1. ТЕПЛОМАССООБМЕН
Задачи.Конвективный
теплообмен
№3
2016 год
2.
• Пример № 1.Рассчитать коэффициент теплоотдачи и тепловой поток
от стенки трубы подогревателя воды. Длина трубы l = 2
м, внутренний диаметр трубы dвн = 16 мм, скорость
течения воды ж = 0,995 м/с, средняя температура воды tж
= 40 °C, а стенки трубы tс = 100 °C. Теплофизические
свойства воды [1] при tж = 40 °C: λж = 0,634 Вт/(м·К); νж
= 0,659·10-6 м2/с; Рrж = 4,3; Gr = 20,72∙106; при tс = 100
°C Рrс = 1,75.
1.Теплотехнические расчеты промышленных печей.
Мастрюков Б.С. – М.: Изд-во «Металлургия», 1972. – 368 с.
3.
Решение.• Рассчитаем значение число Рейнольдса:
wж d вн 0,995 0,016
4
Re ж
2,42 10 .
6
ж
0,659 10
Поскольку Reж > 104, режим течения жидкости турбулентный,
m
n
поэтому воспользуемся формулой
d
d
Nuс c Reг Prг Grг Prг
l
l
и приложением 4 для определения числа Нуссельта
0,016
4
Nu 0,21 2,42 10 4,3
2,0
0 ,8
0,016
7
0,31 10 4,3
2,0
0, 07
102,5
4.
• Определим коэффициент теплоотдачи:0,634
Вт
Nu 102,5
4061,6 2 .
d
0,016
м К
l
• Отношение
50,
d вн
следовательно, и тепловой поток находим по уравнению
Q F tс tж d l tс tж
Q 4061,6 3,14 0,016 2,0 100 40 24487 Вт.
5.
• Пример № 2.• Для отопления гаража используют трубу, в которой
протекает горячая вода. Рассчитать коэффициент
теплоотдачи и конвективный тепловой поток, если
размеры трубы dн = 0,1 м, lтр = 10 м, а температура
стенки трубы tс = 85 °C и воздуха tж = 20 °C.
• Литература:
1.Теплотехнические расчеты промышленных печей.
Мастрюков Б.С. – М.: Изд-во «Металлургия», 1972. – 368 с.
6.
Решение.tж tс 85 20
52,5 С.
Средняя температура стенки: tст
2
2
Теплофизические свойства
температуре [1]:
λв = 2,84·10-2 Вт/(м·К);
νв = 18,2·10-6 м2/с;
Рrв = 0,697;
воздуха
при
средней
Определим коэффициент объемного расширения
β = 1/Т = 1/(273 + 52,5) = 3,1·10-3 1/К.
7.
1. Определим безразмерное число Грасгофаg tс tж d 3
Gr
2
Gr
9,81 3,1 10
3
85 20 0,1
3
18,2 10
6 2
5,97 10 .
6
8.
• 2. По значению произведенияGr Pr 5,97 10 0,697 4,16 10
6
6
• в табл. 1 находим значение коэффициента c = 0,54 и показателя
степени n = 0,25.
• Определим критерий Нуссельта по формуле:
N u c Gr Pr 0,54 4,16 10
n
• Вычисляем
формуле:
коэффициент
конвективной
2,84 10
N u 24,4
dн
0,1
2
6 0, 25
24,4.
теплоотдачи
Вт
6,93 2 .
м К
по
9.
• 3. Определяем конвективный тепловой поток находим поуравнению:
Q F tс tж d н lтр tс tж
Q 6,93 3,14 0,1 10 85 20 1415 Вт.
10.
• Пример № 3.• Вычислить потери тепла в единицу времени с 1 м2
поверхности пода, свода и боковых стен
лабораторной электропечи сопротивления; размеры
кожуха составляют 0,6×0,5×0,75 м. Температура
кожуха tс = 80 °C, температура воздуха в помещении
tв = 20 °C.
11.
Решение.• 1. Плотность теплового потока на наружной поверхности печи
определим из уравнения:
q tс tж
• При заданных значениях температур на поверхности кожуха и
окружающей среды вдали от стенки решение задачи сводится
к определению коэффициента теплоотдачи.
Коэффициент теплоотдачи при
жидкости определяем по формуле
свободном
движении
Nu c Gr Pr ,
а коэффициент и показатель степени из таблицы 1.
n
12.
• Врассматриваемой
задаче
определяющая
температура для всех поверхностей °C,
tж tс 80 20
t
50 С.
2
2
• При этой температуре для воздуха:
νв = 17,95·10-6;
λв = 2,83·10-2 Вт/(м·град);
Рr = 0,698;
β = 1/( + 273) = 3,1∙10-3 1/град.
13.
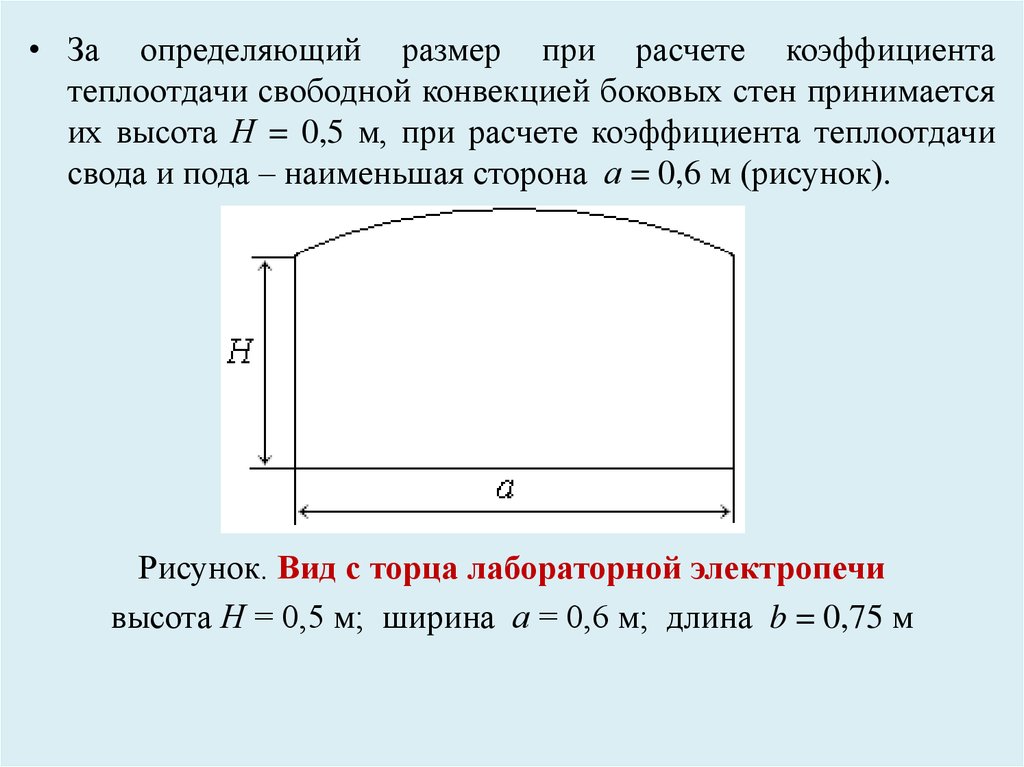
• За определяющий размер при расчете коэффициентатеплоотдачи свободной конвекцией боковых стен принимается
их высота Н = 0,5 м, при расчете коэффициента теплоотдачи
свода и пода – наименьшая сторона а = 0,6 м (рисунок).
Рисунок. Вид с торца лабораторной электропечи
высота Н = 0,5 м; ширина а = 0,6 м; длина b = 0,75 м
14.
• 2. Значение комплекса (Gr·Pr) для боковых стен определим изравенства
g H3
Gr Pr 2 t Pr
в
Gr Pr
9,81 0,5
3
17,95 10
6 2
3
3,1 10 60 0,698 4,94 10 .
8
• По полученному значению комплекса (Gr·Pr) в таблице 1
находим значение коэффициента c = 0,135 и показателя
степени n = 0,333.
15.
• 3. Определим коэффициент теплоотдачи длявертикальных стен, Вт/(м2·град)
N u c Gr Pr .
n
8 0,333
N u 0,135 4,94 10
106.
• Вычисляем коэффициент конвективной теплоотдачи для
вертикальных стен по формуле:
в
2,83 10 2
Вт
Nu
106
6,0 2 .
H
0,5
м К
16.
• 4. Значение комплекса (Gr·Pr) для горизонтальных стенопределим из равенства
g a3
Gr Pr 2 t Pr
в
Gr Pr
9,81 0,6
3
17,95 10
6 2
3
3,1 10 60 0,698 8,54 10 .
8
• По полученному значению комплекса (Gr·Pr) в таблице 1
находим значение коэффициента c = 0,135 и показателя
степени n = 0,333.
17.
• 5. Определим коэффициент теплоотдачи длягоризонтальных стен, Вт/(м2·град)
N u c Gr Pr .
n
8 0,333
N u 0,135 8,54 10
127.
• Вычисляем коэффициент конвективной теплоотдачи для
вертикальных стен по формуле:
в
2,83 10 2
Вт
Nu
127
6,0 2 .
a
0,6
м К
18.
• 6. Поскольку теплоотдающая поверхность свода обращена кверху, полученное значение коэффициента теплоотдачи
следует увеличить на 30 %, т.е. αсв = 1,3∙6,0 = 7,8 Вт/(м2·К), а
теплоотдающая поверхность пода обращена к низу, поэтому
полученное значение коэффициента теплоотдачи следует
уменьшить на 30%, т.е. αпод = 0,7∙6,0 = 4,2 Вт/(м2·К).
7. Вычислим плотности теплового потока по формуле:
q tс tж .
Со свода печи:
Вт
qсв 7,8 80 20 468 2 .
м
С боковых поверхностей
С пода печи
qпод
qбок.ст
Вт
6,0 80 20 360 2 .
м
Вт
4,2 80 20 252 2 .
м
19.
• Пример № 4.• Определить коэффициент теплоотдачи и количество
переданной теплоты при течении воды в
горизонтальной трубе диаметром d = 0,008 м и
длиной, l = 6 м, если скорость течения воды w = 0,1
м/с; температура воды tж = 80 °C; температура стенки
трубы tст = 20 °C.
20.
Решение.• Теплофизические свойства воды при tж = 80 °C:
λж = 0,675 Вт/(м·К);
νж = 0,365·10-6 м2/с;
βж = 6,32·10-4 (1/К)
Рrж = 2,21.
• При температуре стенки Тст = 293 К: Рrст = 7,02.
• При этих значениях рассчитаем число Рейнольдса:
Re жd
w d
0,1 0,008
2190.
6
ж
0.365 10
21.
• Значение критерия Нуссельта определим из уравнения:N uжd
Re0ж,d33
0,33
0, 43
0,1
0,15 Re жd Prж Grжd
Prж
Prст
13,2
• Температурный напор
0, 43
Prж
0, 25
Prж
Prст
1,4
.
0, 25
0,75
t tж tст 60 .
3
g
t
t
d
с
ж
• Число Грасгофа: Gr
2
Gr
Grж0d,1 4,12
9,81 6,32 10 60 0,008
4
3
0,365 10
6 2
1,43 106.
22.
• Находим значение критерия НуссельтаN uжd 0,15 13,2 1,4 4.12 0,75 8,56.
• Откуда
ж
0,675
Вт
N uжd
8,56
724 2 .
d
0,008
м К
Поправку на длину трубы вводить не следует, так как
l
50
d
Количество передаваемой теплоты через всю трубу
Q d l tж tст
Q 724 3,14 0,008 6 60 6540 Вт.
23.
• Пример № 5.• Определить коэффициент теплоотдачи α воздуха,
протекающего со скорость w = 10 м/с, стенке прямой
трубы диаметром d = 0,1 м и длиной, l = 2 м. Средняя
температура воздуха tж = 120 °C.
24.
Решение.• Теплофизические свойства воздуха при средней температуре
tж = 120 °C:
λж = 0,0334 Вт/(м·К);
νж = 25,45·10-6 м2/с;
• При этих условиях рассчитаем число Рейнольдса:
wж d
10 0,1
39200.
6
ж
25,45 10
Re жd
• Значение критерия Нуссельта определим из уравнения:
N uжd
0 ,8
0,018 Re жd .
0 ,8
Re жd
• Подставляя значение в уравнение, получаем:
N uжd 0,018 4730 85,2.
4730
25.
• ОткудаТак как
l
ж
0,0334
Вт
N uжd
85,2
28,4 2 .
d
0,1
м К
l
2
20 50
d 0,1
, то необходимо ввести поправку
взятую из таблицы.
Таблица
l d
1
l
1,9
4
5
10
15
20
30
40
50
1,7 1,44 1,28 1,18 1,13 1,05 1,02 1,0
С поправкой коэффициент теплоотдачи равен:
Вт
д l 28,4 1,13 32,2 2
м К
























 Физика
Физика








