Классическая теория гармонического кристалла. Гармоническое приближение. Адиабатическое приближение

1.

Тема 3 (Лекция 5-6)
КЛАССИЧЕСКАЯ ТЕОРИЯ
ГАРМОНИЧЕСКОГО КРИСТАЛЛА
ГАРМОНИЧЕСКОЕ ПРИБЛИЖЕНИЕ
АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ
ОДНОМЕРНАЯ МОНОАТОМНАЯ РЕШЕТКА БРАВЭ
ОДНОМЕРНАЯ РЕШЕТКА С БАЗИСОМ
ТРЕХМЕРНАЯ МОНОАТОМНАЯ РЕШЕТКА БРАВЭ
УДЕЛЬНАЯ ТЕМПЛОЕМКОСТЬ КЛАССИЧЕСКОГО
КРИСТАЛЛА
1

2.

1. Считаем, что среднее равновесное положение каждого иона
совпадает с узлом решетки Бравэ.
с каждым ионом связан определенный узел R решетки Бравэ,
относительно которого он совершает колебания,
узел R есть лишь среднее положение
фиксированное мгновенное положение.
иона,
а
не
его
2. Принимаем, что типичные отклонения каждого иона от его
положения равновесия малы по сравнению с расстоянием
между ионами.
2

3.

u (R) — отклонение от равновесия для иона, равновесное положение которого есть R

4.

P(R) — импульс атома с равновесным положением R, М — масса атома.

5.

ГАРМОНИЧЕСКОЕ ПРИБЛИЖЕНИЕ
a

6.

7.

НОРМАЛЬНЫЕ МОДЫ
ОДНОМЕРНОЙ МОНОАТОМНОЙ РЕШЕТКИ БРАВЭ
K= f ''(a)
f (х) — энергия взаимодействия двух
ионов, находящихся на расстоянии х вдоль
прямой.
7

8.

Уравнения движения
-p/a
-
p/a
8

9.

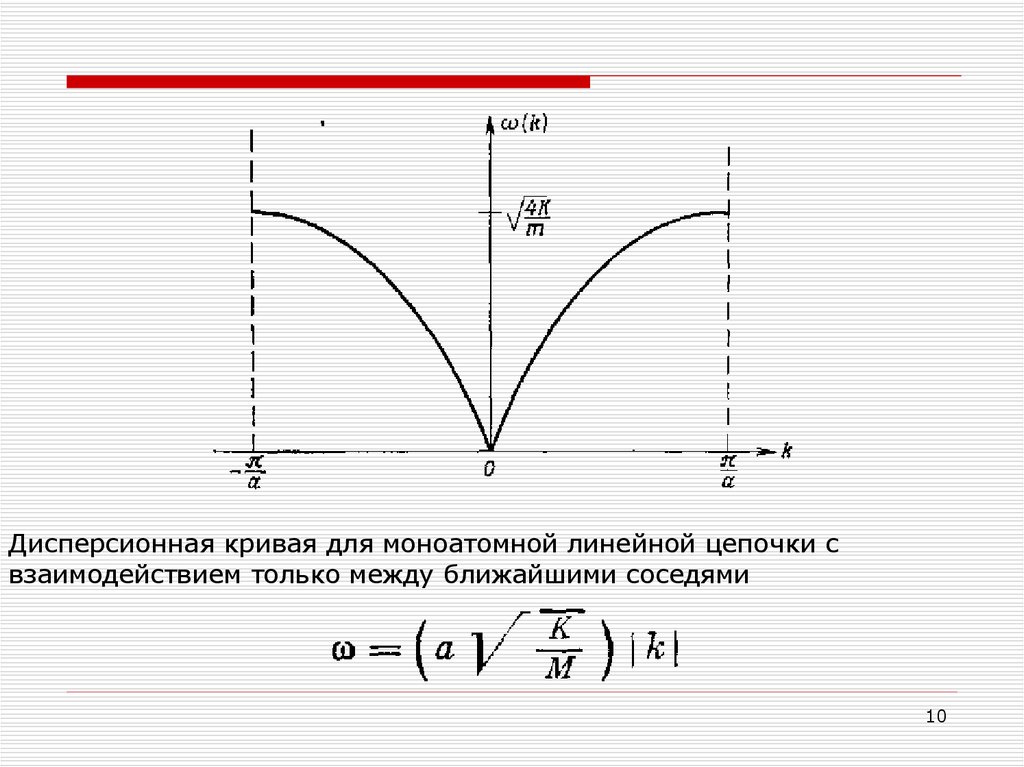
поэтому при заданном k решение существует, если w = w (k), где
9

10.

Дисперсионная кривая для моноатомной линейной цепочки с
взаимодействием только между ближайшими соседями
10

11.

НОРМАЛЬНЫЕ МОДЫ ОДНОМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
где через u1(na) -смещение иона, совершающего колебания вблизи узла
nа, а через u2(nа) — смещение иона, колеблющегося вблизи узла nа+d.
К≥G
11

12.

12

13.

Для каждого из N значений k имеется два решения, что дает 2N
нормальных мод, как должно быть при 2N степенях свободы (по два
иона в каждой из N элементарных ячеек).
13

14.

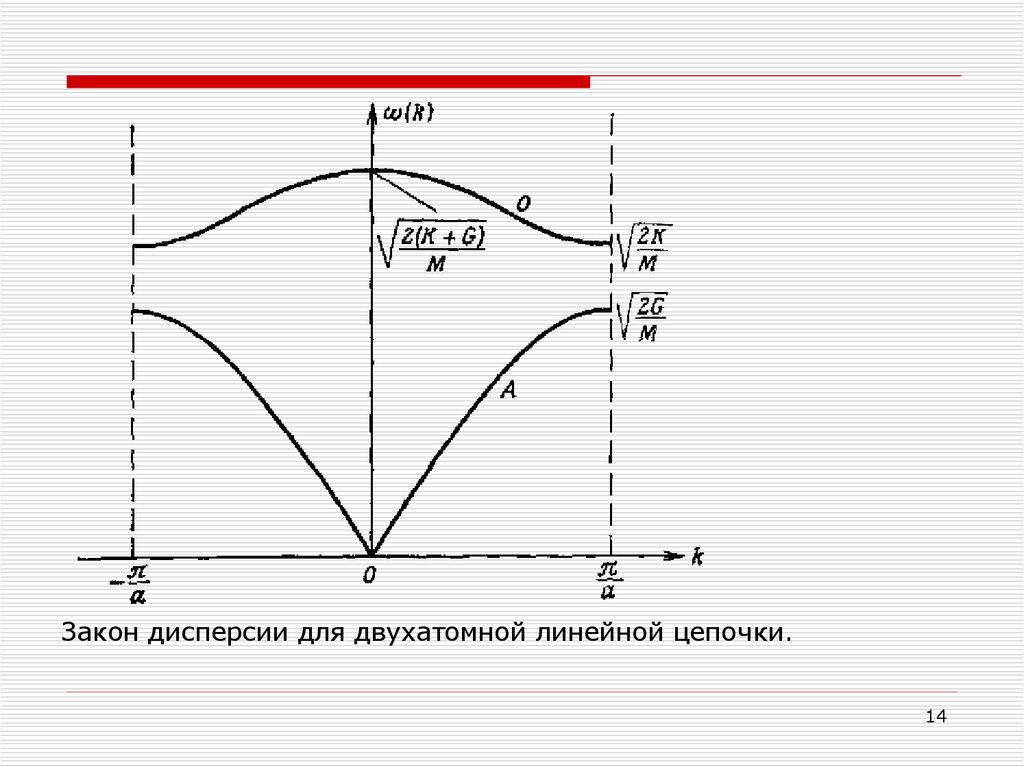
Закон дисперсии для двухатомной линейной цепочки.
14

15.

Случай 1.
e2 = e1
акустическая (а) и оптическая (б) моды в двухатомной линейной цепочке
Короткие волны распространяются медленнее, чем длинные
Цепочка из одинаковых атомов при распространении акустических волн ведет как упругая
струна только при l>>2a
15

16.

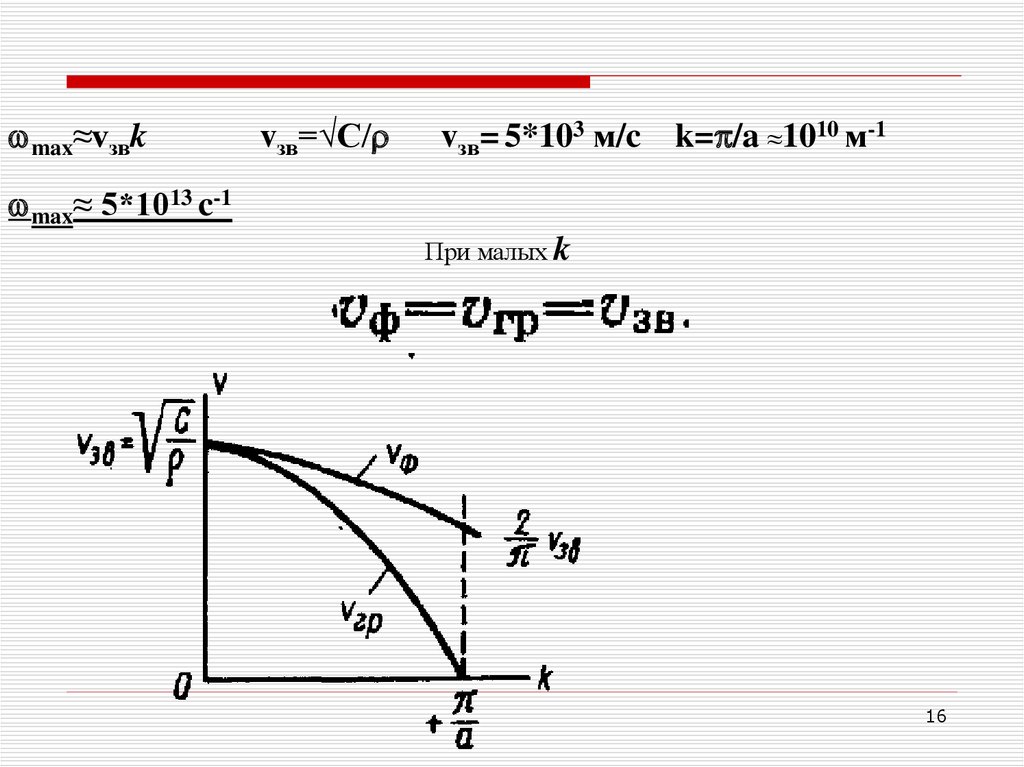
wmax≈vзвk
vзв=√C/r
vзв= 5*103 м/c
k=p/a ≈1010 м-1
wmax≈ 5*1013 c-1
При малых k
16

17.

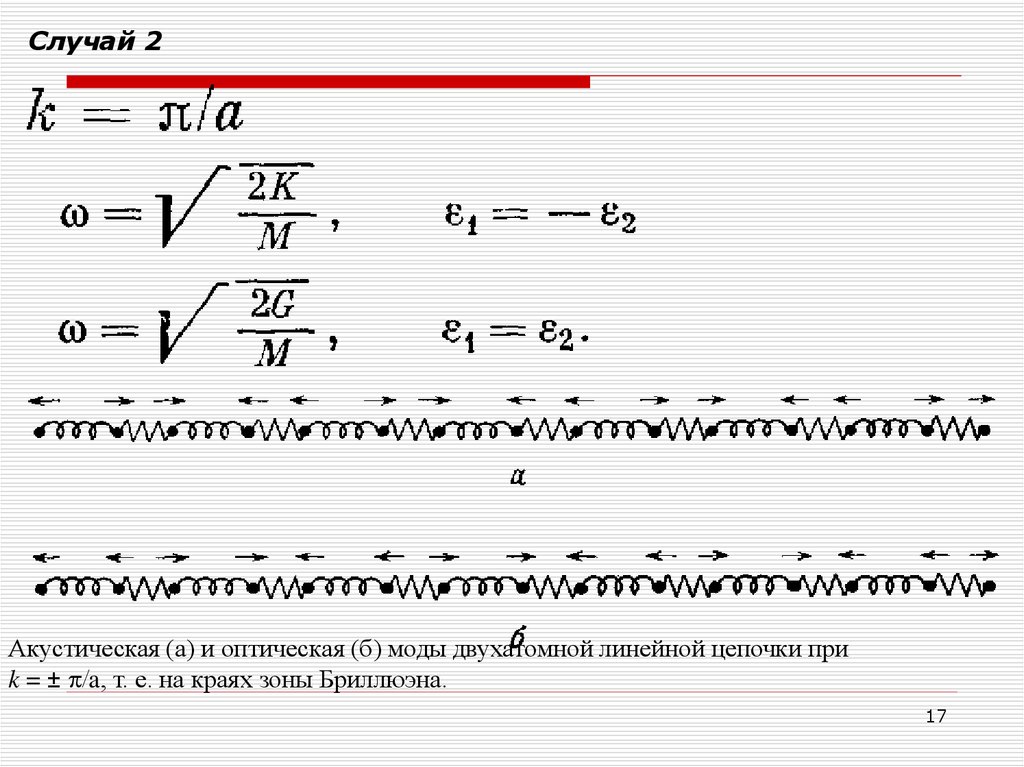
Случай 2
Акустическая (а) и оптическая (б) моды двухатомной линейной цепочки при
k = ± p/a, т. е. на краях зоны Бриллюэна.
17

18.

Случай 3. К >> G. В первом порядке по отношению G/K
Случай 4. К = G.
Моноатомная решетка Бравэ, с постоянной решетки а/2
18

19.

19

20.

20

21.

НОРМАЛЬНЫЕ МОДЫ
МОНОАТОМНОЙ ТРЕХМЕРНОЙ РЕШЕТКИ БРАВЭ
21

22.

Первое свойство симметрии
22

23.

Второе свойство симметрии
или
Третье свойство симметрии
23

24.

24

25.

вектор поляризации нормальной моды e
Борна-Кармана условие
25

26.

eiK-R ≡1
N неэквивалентных значений k
26

27.

динамическая матрица
27

28.

D(k) есть четная функция от k и действительная матрица.
матрица D(k) симметрична
28

29.

в длинноволновом пределе (при малых k)
√
29

30.

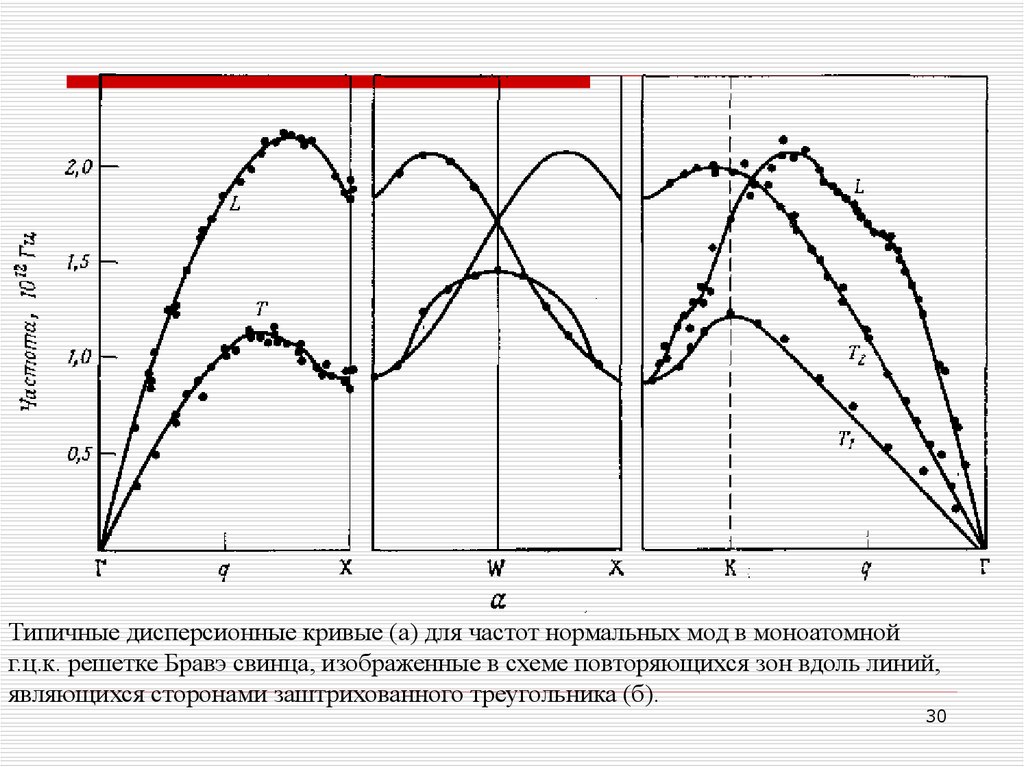
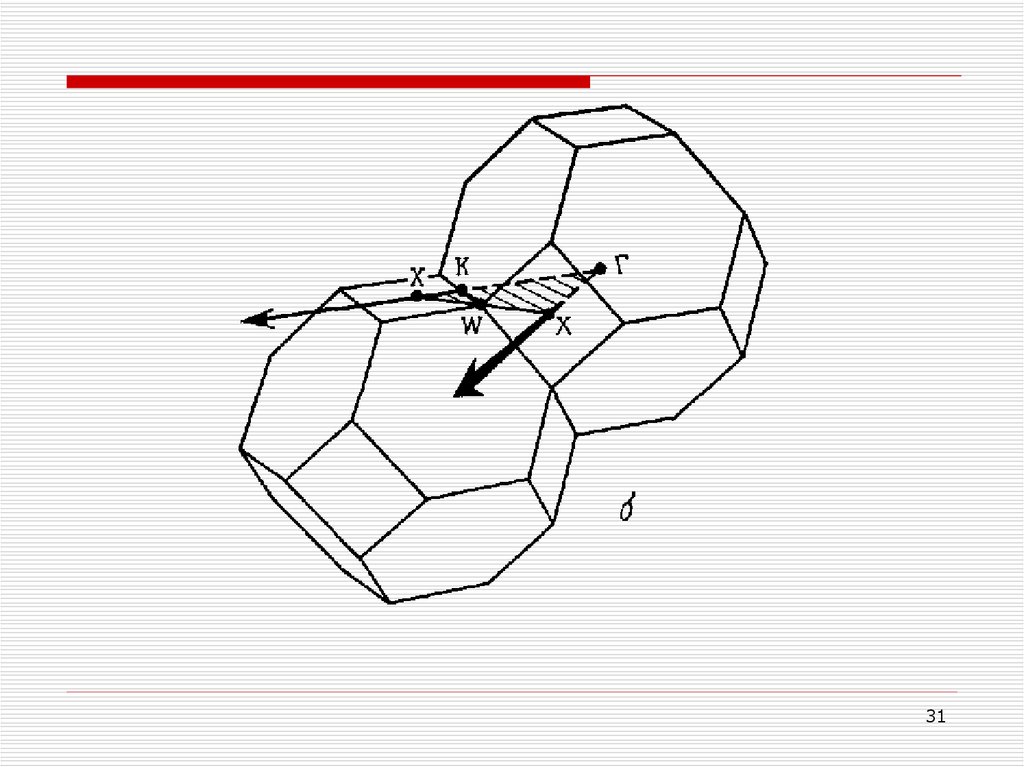
Типичные дисперсионные кривые (а) для частот нормальных мод в моноатомной
г.ц.к. решетке Бравэ свинца, изображенные в схеме повторяющихся зон вдоль линий,
являющихся сторонами заштрихованного треугольника (б).
30

31.

31

32.

НОРМАЛЬНЫЕ МОДЫ
ТРЕХМЕРНОЙ РЕШЕТКИ С БАЗИСОМ
Для каждого значения k имеется Зр нормальных мод, где р — число ионов в
базисе.
Частоты ws (k) (s = 1, . . ., Зр) являются функциями k и обладают
периодичностью обратной решетки;
3 из Зр ветвей — акустические;
3 (р — 1) ветвей — оптические;
Векторы поляризации нормальных мод уже не связаны простыми соотношениями ортогональности типа
32

33.

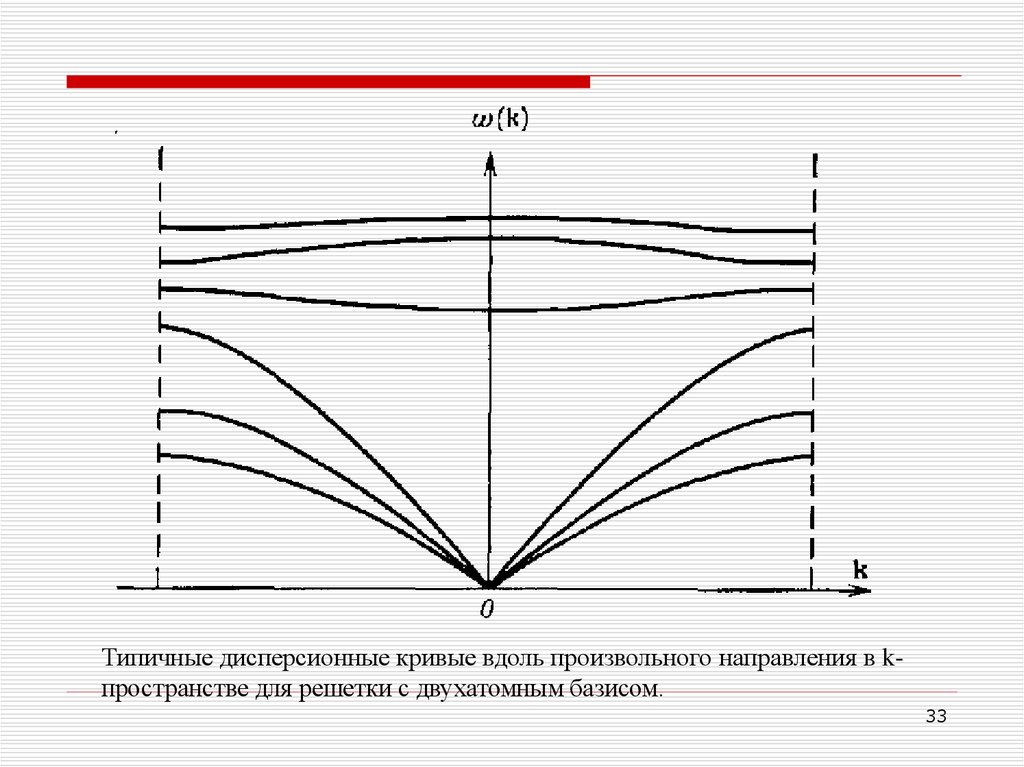
Типичные дисперсионные кривые вдоль произвольного направления в kпространстве для решетки с двухатомным базисом.
33

34.

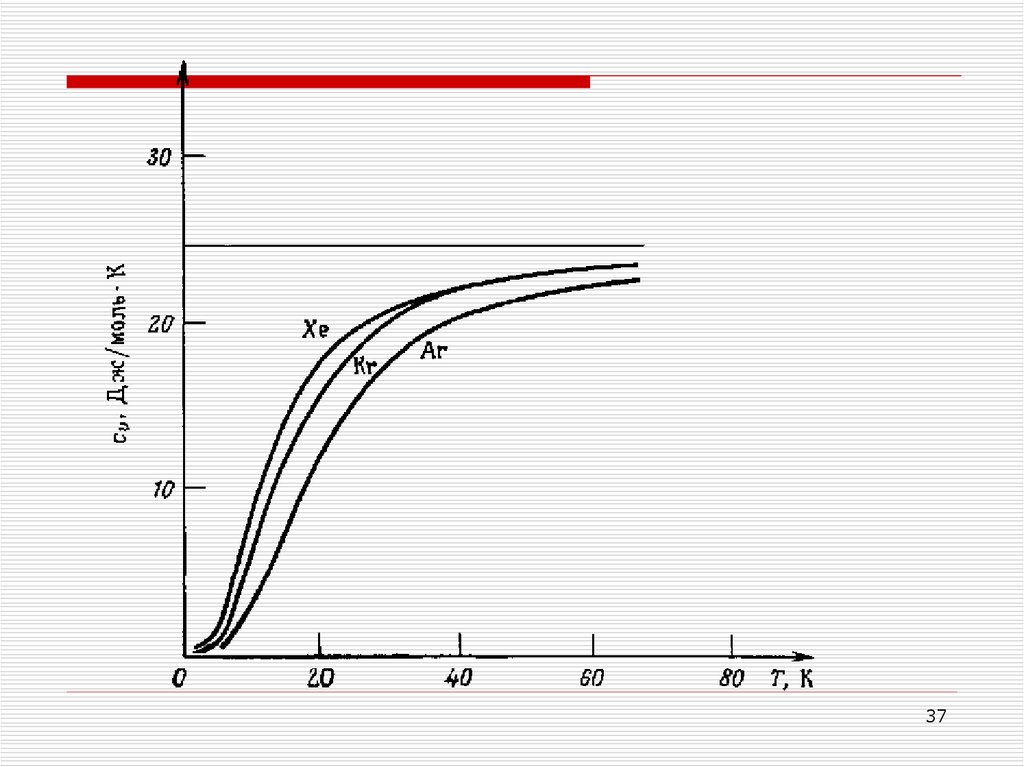
Удельная теплоемкость вещества отнесенная к 1 молю – энергия, которую необходимо
сообщить молю вещества, чтобы повысить температуру на 1 градус
Дюлонг-Пти – при высоких температурах есть величина постоянная, не зависящая от
температуры – 25 Дж/моль*К
Объяснение в рамках классической физики – из закона равномерного распределения
энергии по степеням свободы
34

35.

35

36.

36

37.

37

38.

38

39.

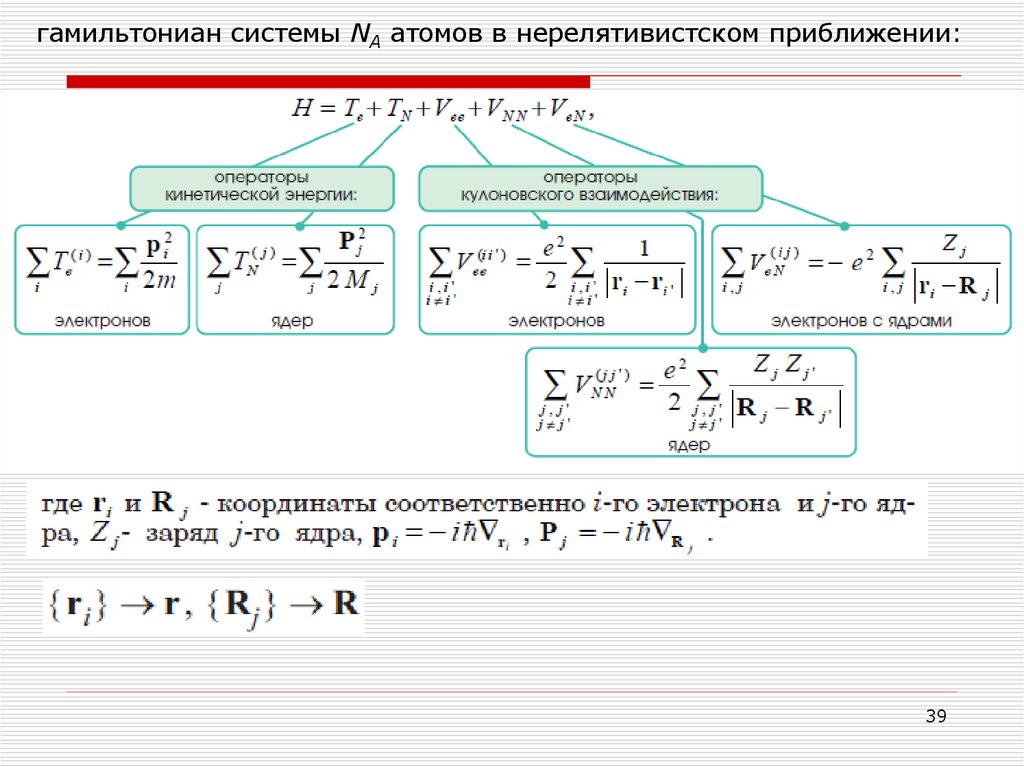
гамильтониан системы NA атомов в нерелятивистском приближении:
39

40.

40

41.

41
Собственные значения и собственные функции зависят от координат Х как от параметров

42.

Движение ядер ограничено малой окрестностью Х0
Х-Х0 -малое
u- ядерная координата
42

43.

43

44.

44

45.

Решение 0-го порядка
45

46.

46

47.

47

48.

Гармоническое приближение
48

49.

49

50.

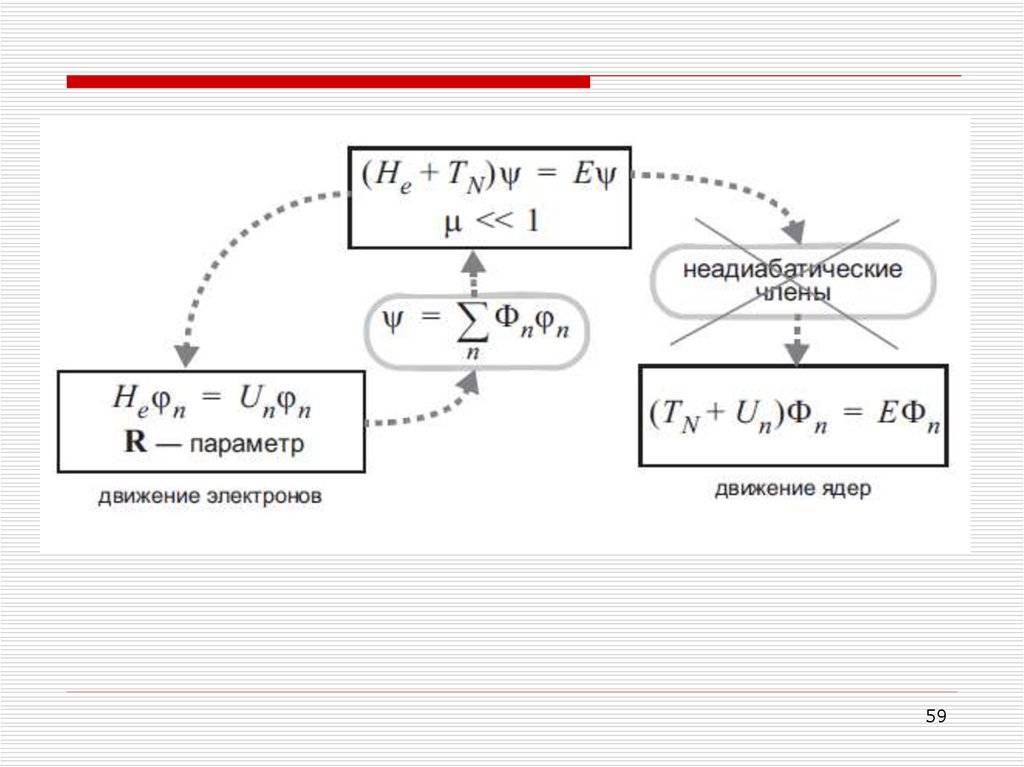
Оператор He не содержит производных по R и зависит от R как от параметра .
Пусть jn (r ,R) и Un(R) - собственные функции и собственные значения
электронного гамильтониана He, соответственно
y(r ,R, t )
50

51.

×
dr
51

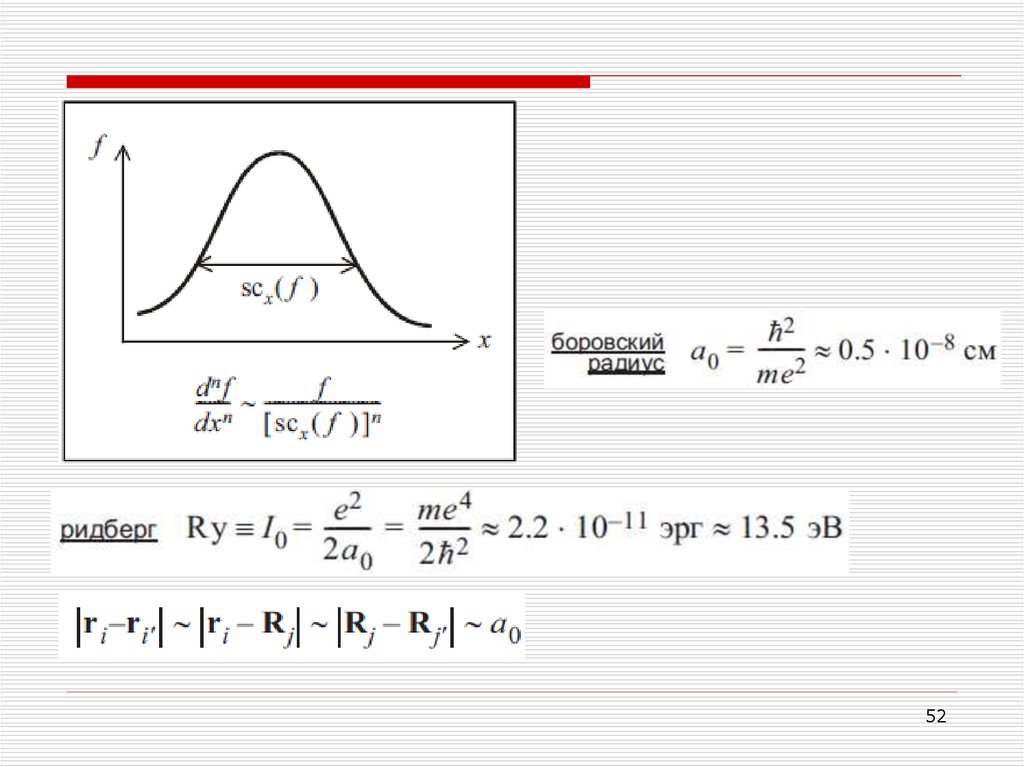
52.

52

53.

- квантовомеханическое
усреднени
N - полное число атомов в системе
53

54.

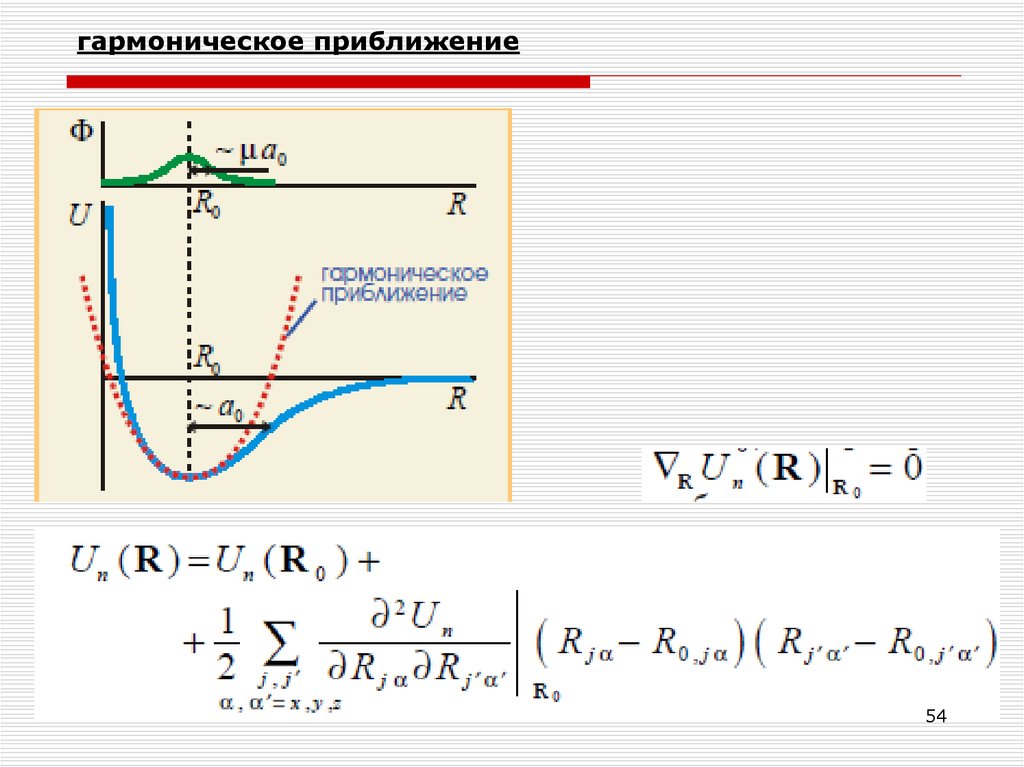
гармоническое приближение
54

55.

Теорема вириала для гармонического осциллятора:
характерные значения импульса и
амплитуды колебаний
амплитуда колебаний
55

56.

Энергия колебаний
Для энергии тепловых колебаний ядер в твердом теле
где T - температура, Tпл < 103 K - температура плавления, - постоянная Больцмана (1.38⋅10− 16 эрг K)
56

57.

Неадиабатические слагаемые
57

58.

в адиабатическом приближении
58

59.

59

60.

60