Сдвиговая прочность кристаллов. Модели ядра дислокаций. Барьер Пайерлса. Механизмы пластической деформации

1. Физика реального кристалла

10. Сдвиговая прочность кристаллов.
Модели ядра дислокаций. Барьер
Пайерлса. Механизмы пластической
деформации.
Профессор Б.И.Островский
[email protected]

2.

Прочность кристаллов на сдвиг

3. Атомная структура ядра дислокации

Пластичные
материалы
можно ковать!
Fe, Cu – пластичны;
??
Si, Ge – хрупки

4.

Пластическая деформация кристаллов
A
x
x
b
= x/a, справедлив
закон Гука: = G = Gx/a. При этом (x) A2 x/b
Для малых сдвиговых деформаций,
A
A G/2
Experimentally:
10-4 to 10-8 G
Напряжение течения

5.

= -dU/dx
Модель
Френкеля

6.

7.

8.

Экспериментальные факты

9.

Барьер Пайерлса
Связи в плоскости
скольжения рвутся
локально, одна за
другой!
U
lFl = S = -dU/dx

10.

Барьер Пайерлса
Ep << kB T
Критическое сдвиговое
напряжение
p 10 -3 10 -4 G

11.

Модель Пайерлса - Набарро
«ширина»
ядра
дислокации

12.

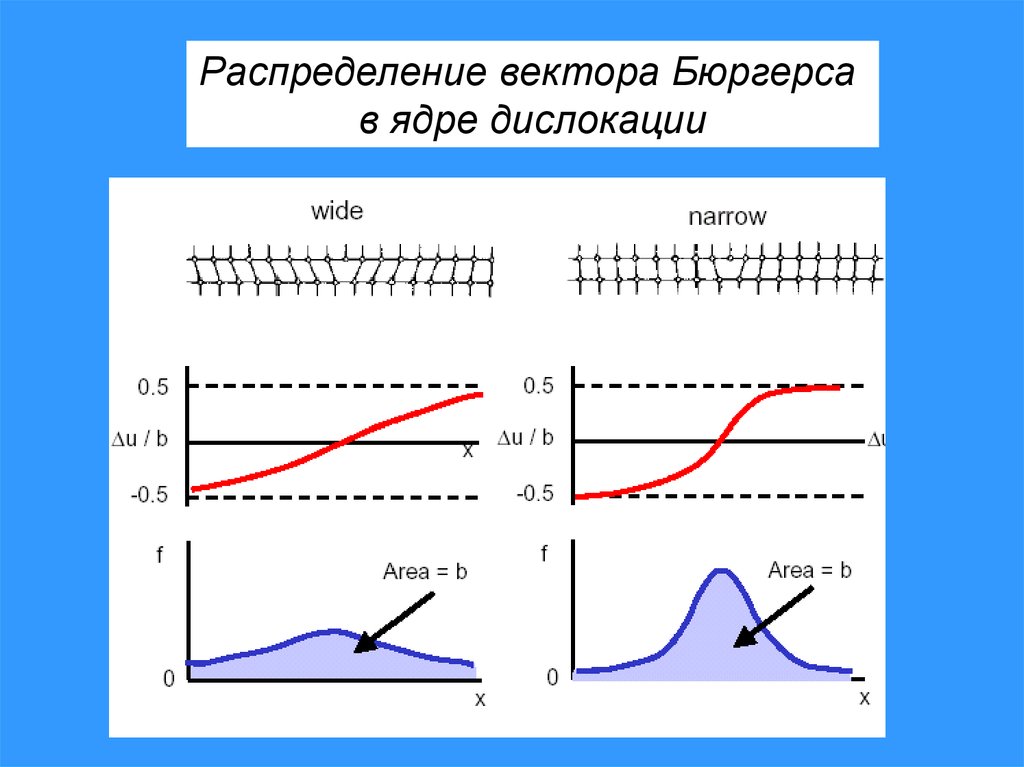
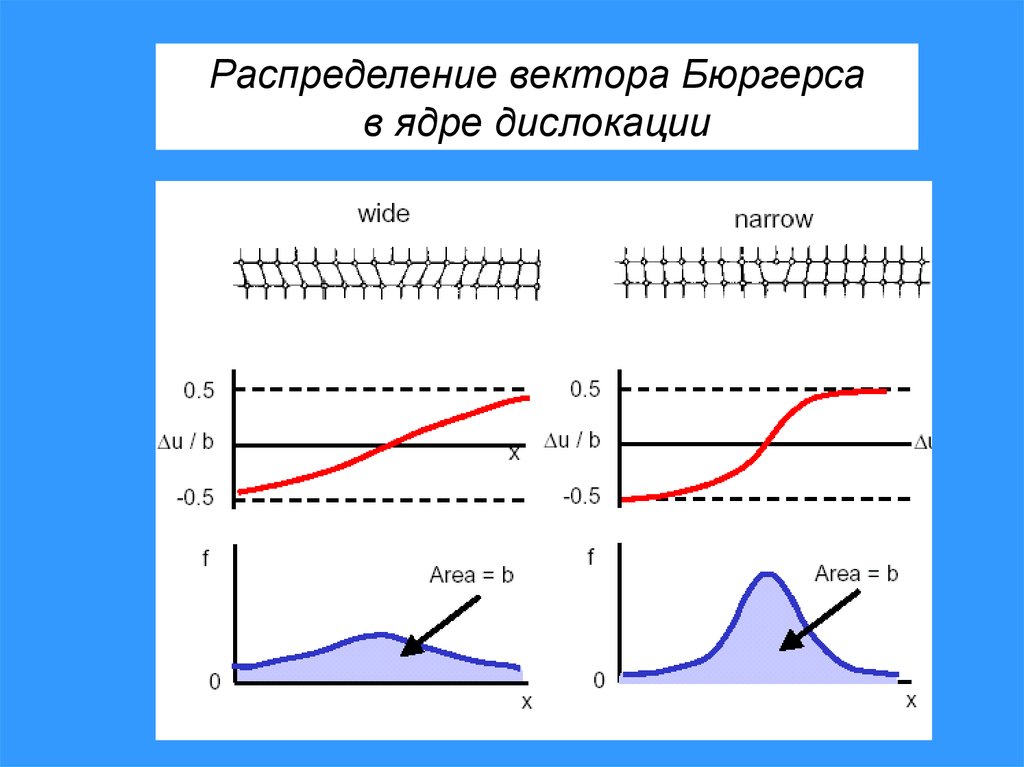
Распределение вектора Бюргерса
в ядре дислокации

13.

14.

15.

Чтобы получить кон-

16.

Сдвиг одной половины
кристалла относительно
другой на b/2
Сожмем верхнюю половину
кристалла и растянем нижнюю

17.

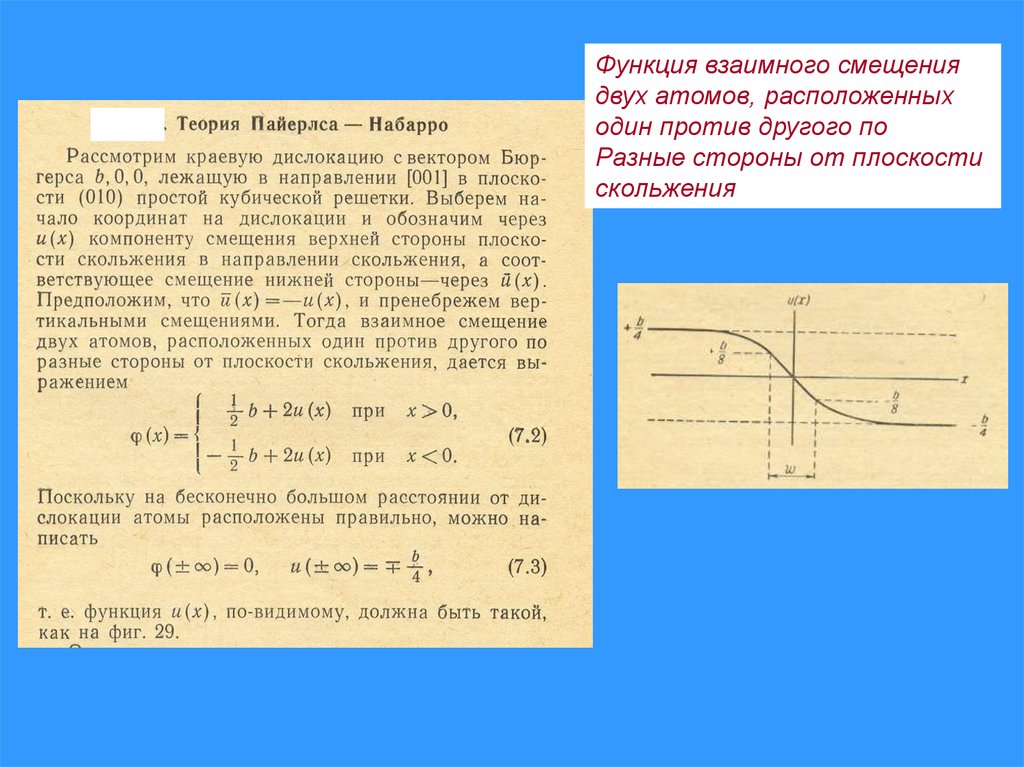
Функция взаимного смещения
двух атомов, расположенных
один против другого по
Разные стороны от плоскости
скольжения

18.

Расположение n одноименных дислокаций
в плоскости скольжения
=
D = Gb/2 (1- )

19.

Распределение вектора Бюргерса
в ядре дислокации

20.

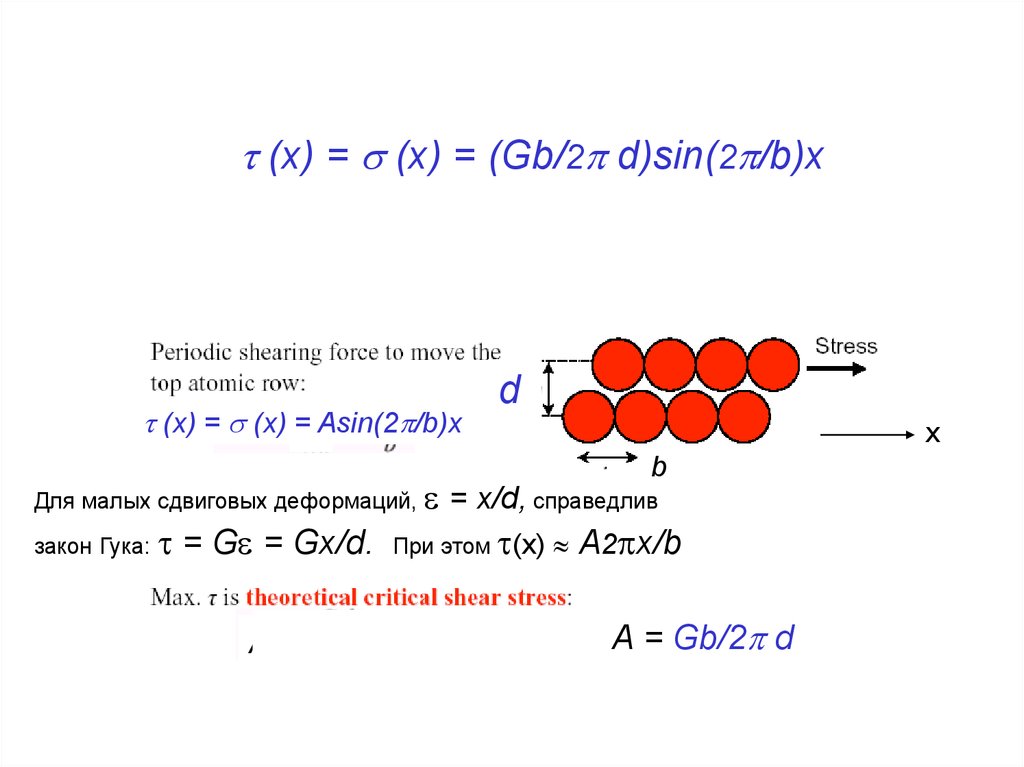
(x) = (x) = (Gb/2 d)sin(2 /b)x
(x) = (x) =AAsin(2 x/b)x
d
x
b
= x/d, справедлив
закон Гука: = G = Gx/d. При этом (x) A2 x/b
Для малых сдвиговых деформаций,
A
A = Gb/2 d

21.

22.

23.

D = Gb/2 (1- );
для сдвиговых напряжений, полученных на основе
континуального подхода Вольтерра
b/4
- определяет «ширину»
2
ядра дислокации
- b/4

24.

25.

Пайерловский рельеф кристалла

26.

= d/2(1 - ) (3/4)d;
1/3 –
exp(-3 d/b) 2x10 -4 (ГЦК решетка)
d/b =
20.32
b)
Коэффициент
Пуассона

27.

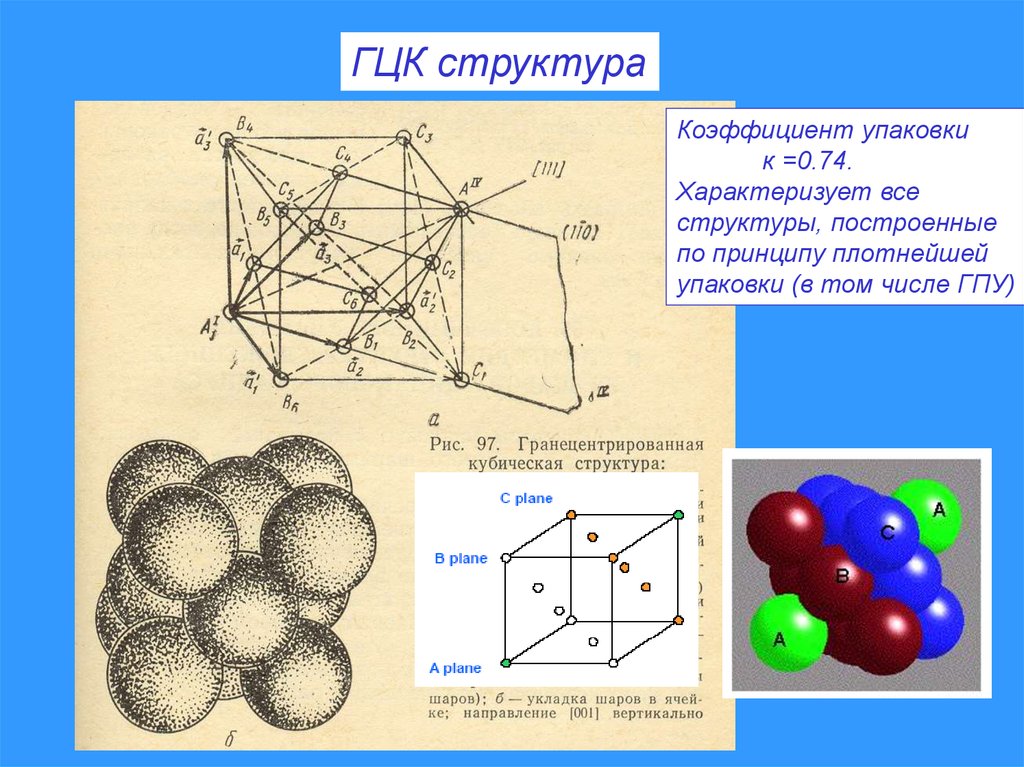
ГЦК структура
Коэффициент упаковки
к =0.74.
Характеризует все
структуры, построенные
по принципу плотнейшей
упаковки (в том числе ГПУ)

28.

p 10 -4 G
(ГЦК решетка)
Ep = p b2/2 10 -4 Gb2
Что в пересчете на одну связь дает:
Epbond 5 x 10 -4 эв
Для сравнения: kB T = 1.4 10-16 эрг/К x 300 К 4x 10-14 эрг
3x10-2 эв

29.

Оценки упругой энергии дислокации
При обычных значениях плотности дислокаций
=107 см-2, среднее
расстояние между ними составляет R -1/2 3.10-4 см, что дает
для
и
10
полн /L
=
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
-4 эрг/см
4.10
/L
=
полн
Что в пересчете на одну связь дает:
Ebond
= 4.10 -4 эрг/см x 2.10 -8 см
= 8.10-12 эрг
5 эв

30.

Энергия (барьер) Пайерлса
Ep << kB T
p 10 -3 10 -4 G

31.

Summary
p exp(-kd/a)
a - min
Пластическая деформация - движение и размножение
дислокаций в плоскости скольжения

32.

Дислокации в гранецентрированной
кубической решетке
Дислокационные сетки
с тройными узлами

33.

34.

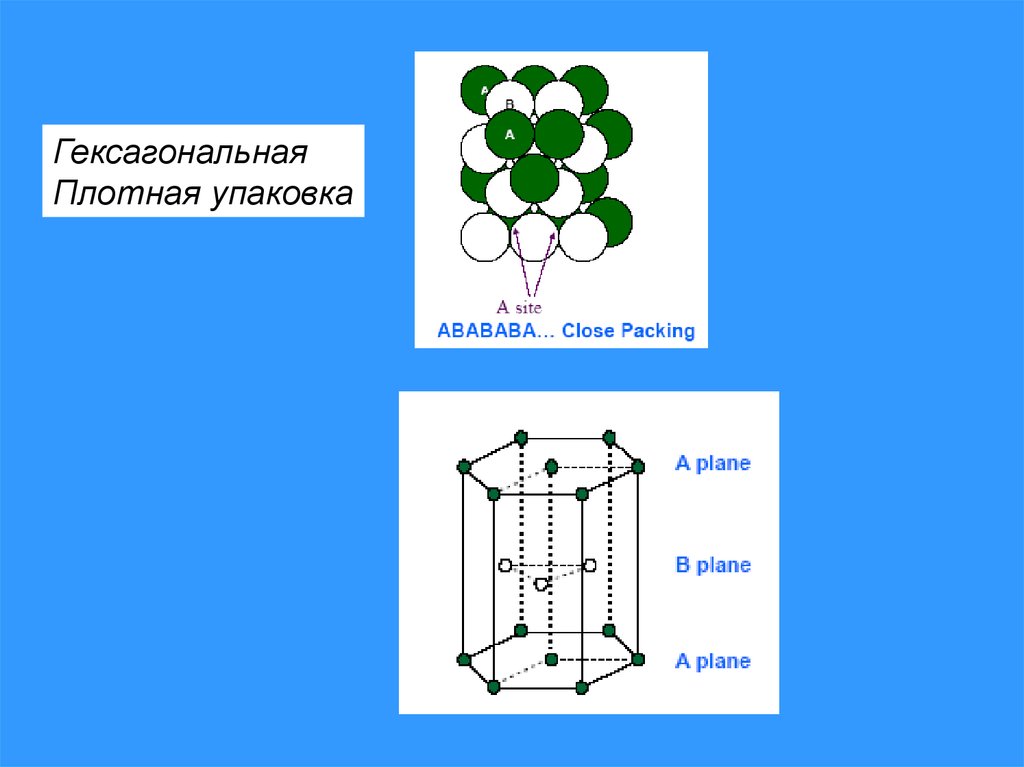
Гексагональная
Плотная упаковка

35.

36.

Common crystal structures in metals:
– Face centered cubic (fcc): ABCABC…
packing: Ni, Cu, Ag, Al, Au
– Hexagonal close packed (hcp): ABABAB
… packing: Mg, Zn, Co, Ti

37.

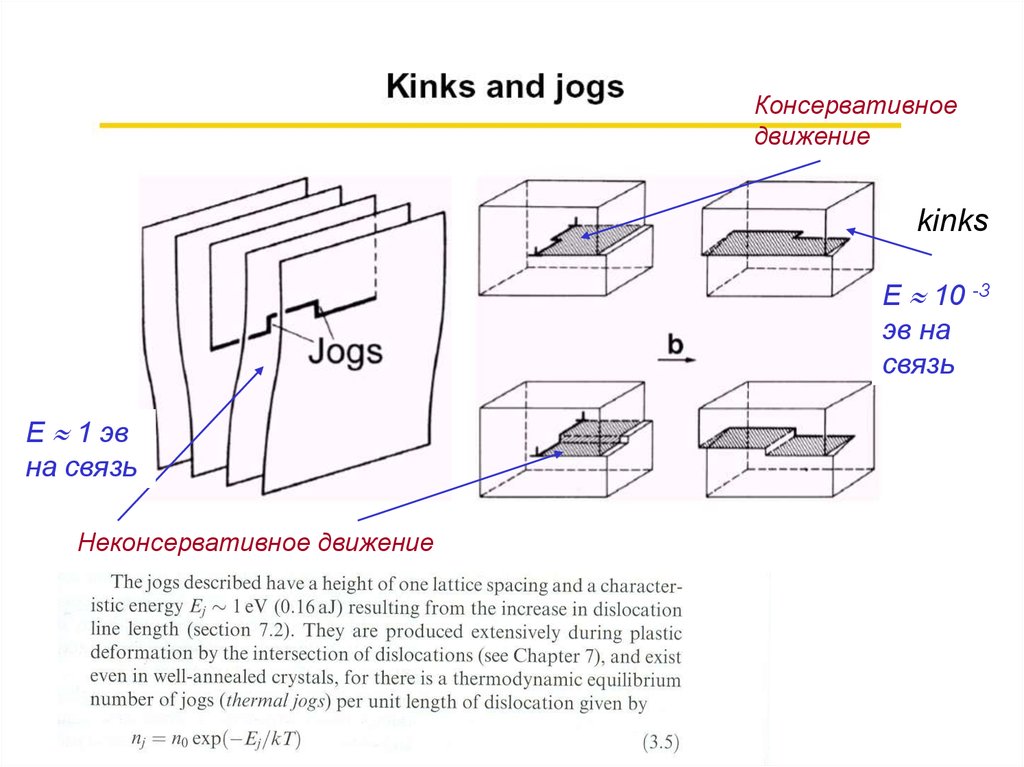
Консервативное
движение
kinks
Е 10 -3
эв на
связь
Е 1 эв
на связь
Неконсервативное движение

38.

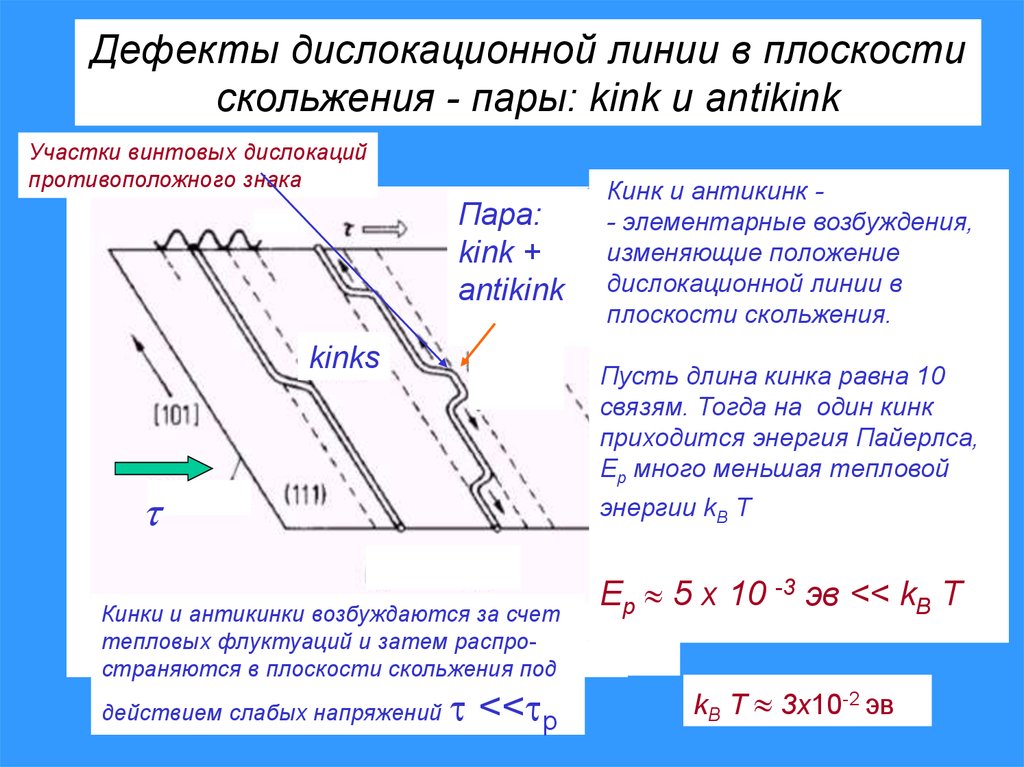
Дефекты дислокационной линии в плоскости
скольжения - пары: kink и antikink
Участки винтовых дислокаций
противоположного знака
Пара:
kink +
antikink
kinks
Пусть длина кинка равна 10
связям. Тогда на один кинк
приходится энергия Пайерлса,
Ep много меньшая тепловой
энергии kB T
Кинки и антикинки возбуждаются за счет
тепловых флуктуаций и затем распространяются в плоскости скольжения под
действием слабых напряжений
Кинк и антикинк - элементарные возбуждения,
изменяющие положение
дислокационной линии в
плоскости скольжения.
<< p
Ep 5 x 10 -3 эв << kB T
kB T 3x10-2 эв

39.

Потенциал Пайерлса (1)
w exp ( F/kBT)
- принцип Больцмана

40.

41.

Потенциал Пайерлса (2)
Дислокации не могут
спонтанно появляться
в кристалле - неравновесный дефект, однако уже
существующие дислокации
могут свободно менять
свою конфигурацию и
перемещаться в плоскости
скольжения
Ep << E0
Ep < kB T

42.

Заключительные замечания
Необходимо отметить, что величины энергии Пайерлса Ep и
критического напряжения сдвига p чрезвычайно чувствительны
к природе межатомных сил и характеру упаковки атомов в
элементарной ячейке.
p 10 -4 10 -5 G
p 10 -2
для ГЦК и ГПУ металлов;
для ковалентных кристаллов типа
кремния и алмаза