Похожие презентации:
Упругие поля (поля напряжений) вокруг дислокаций. Энергия дислокаций. Термодинамика дислокаций
1. Физика реального кристалла
8. Упругие поля (поля напряжений)вокруг дислокаций. Энергия дислокаций.
Взаимодействия между дислокациями.
Термодинамика дислокаций.
Профессор Б.И.Островский
ostr@cea.ru
2. Упругие поля и напряжения вокруг дислокаций
3.
Поле смещений вокруг винтовой дислокацииЦилиндрические
координаты:
r, , z
x2
y2
+ =
tg = y/x
r2;
uz =
uz(x,y)
4.
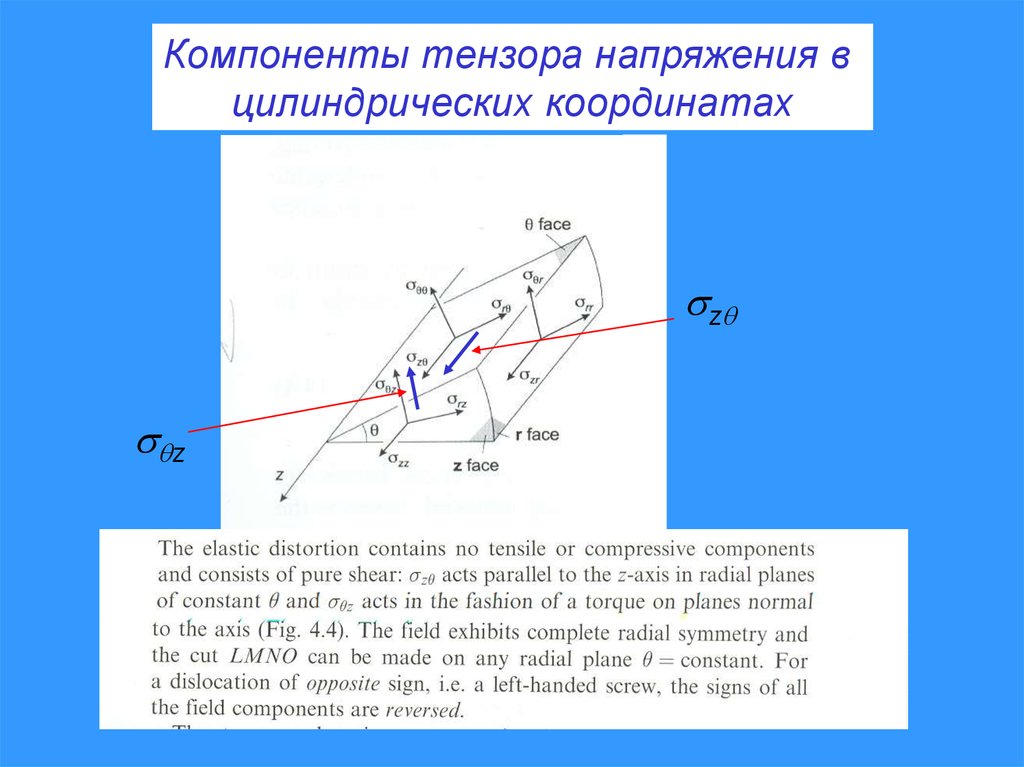
Компоненты тензоров напряжений и деформаций вцилиндрических координатах
используя соотношения:
и, аналогичным образом, для сдвиговых деформаций,
получаем:
5.
Компоненты тензора напряжения вцилиндрических координатах
z
z
6.
Упругие поля искажений вокруг дислокацийявляются дальнодействующими!
Отличные от нуля компоненты ij и kl убывают с
расстоянием от дислокации как r -1,
r -1
7. Замечательная аналогия с магнитным полем прямолинейного проводника
B J/R ;B - аксиальный
вектор
Винтовая дислокация
направлена вдоль оси x3 =z
r -1
8.
Электрическое поле равномерно заряженнойпрямолинейной нити
Теорема Гаусса –
- Остроградского
9.
10.
Упругая энергия дислокацииПолная энергия дислокации состоит из двух частей:
Плотность упругой энергии, запасенной в дислокации:
8
2
полн
2
=
Полная энергия, запасенная в полом цилиндре радиуса R и длины L :
L
2
R
2/8 2) dz d rdr/r2 = L
=
(Gb
полн
0
0
L
r0
Или на единицу длины дислокации:
полн /L
=
dV
11.
Оценки упругой энергии дислокацииПри обычных значениях плотности дислокаций
=107 см-2, среднее
расстояние между ними составляет R -1/2 3.10-4 см, что дает
для
и
10
полн /L
=
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
-4 эрг/см
4.10
/L
=
полн
Что в пересчете на одну связь дает:
Ebond
= 4.10 -4 эрг/см x 2.10 -8 см
= 8.10-12 эрг
5 эв
12.
Поле напряжений прямой краевой дислокации(сплошная изотропная среда)
ux = ux(x,y)
uy = uy(x,y)
Плоское деформированное
состояние:
E =2G (1+ )
uz = 0
-1 < < 1/2
13.
Вычисление компонент тензоровдеформации и напряжений
ux = ux(x,y)
uy = uy(x,y)
14.
Поля упругих смещений вокругпрямолинейной краевой дислокации
15.
yx
16.
Компоненты поля напряжений длякраевой дислокации
17.
Компоненты тензора напряжений в случаевинтовой дислокации
Gb/2 (1- )
-1 < < 1/2
Вывод: все энергетические оценки, выполненные ранее
для винтовых дислокаций, остаются справедливыми и
для краевых дислокаций
18. Силы, действующие на дислокации
19.
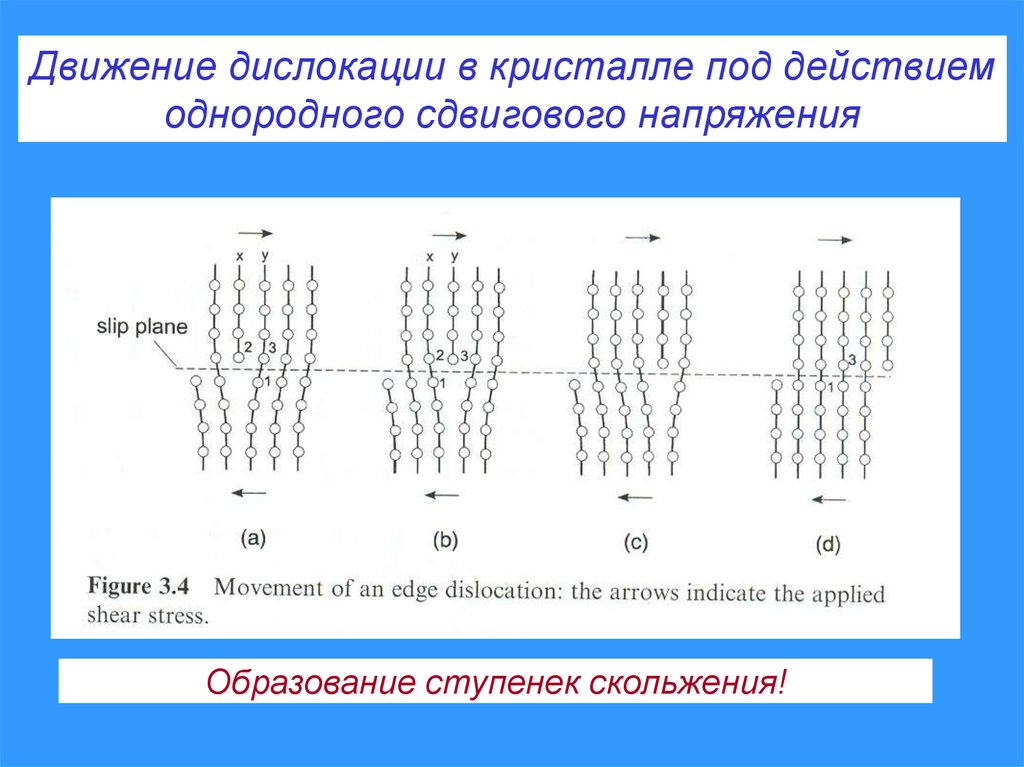
Движение дислокации в кристалле под действиемоднородного сдвигового напряжения
Образование ступенек скольжения!
20.
Сила, действующая на единицу длины дислокацииGj =bi ij
вектор
Сила всегда направлена
перпендикулярно линии
дислокации
21.
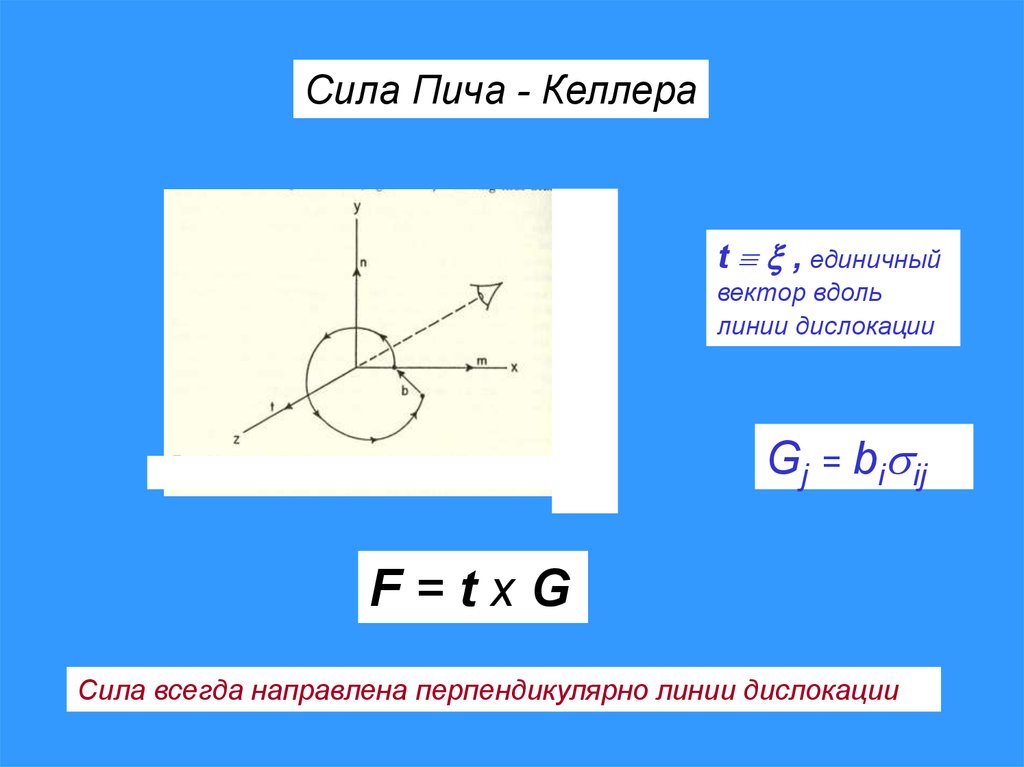
Формула Пича - Келлера(сила, действующая на единицу длины дислокации)
t , единичный
вектор вдоль
линии дислокации
Сила всегда направлена
перпендикулярно линии
дислокации
22.
Сила Пича - Келлераt , единичный
вектор вдоль
линии дислокации
Gj = bi ij
F=txG
Сила всегда направлена перпендикулярно линии дислокации
23.
Сила Пича - Келлера24. Взаимодействие дислокаций
25.
Силы между дислокациями?
Аналогия с заряженным конденсатором
26.
Взаимодействие двух параллельныхвинтовых дислокаций
27.
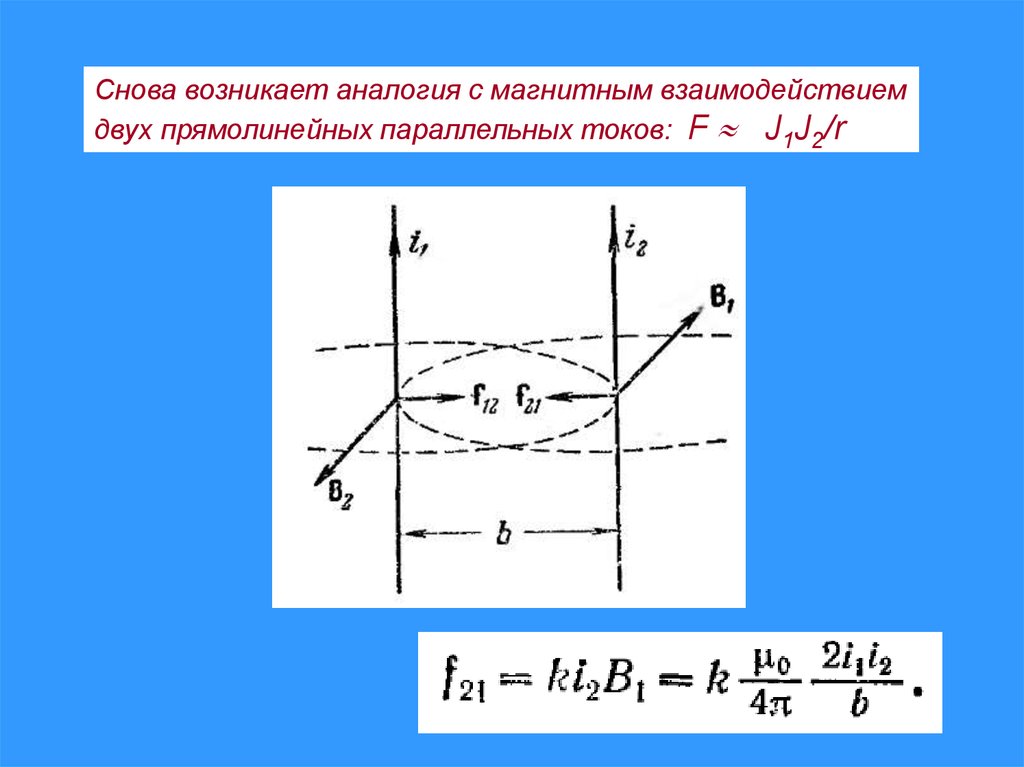
Снова возникает аналогия с магнитным взаимодействиемдвух прямолинейных параллельных токов: F J1J2/r
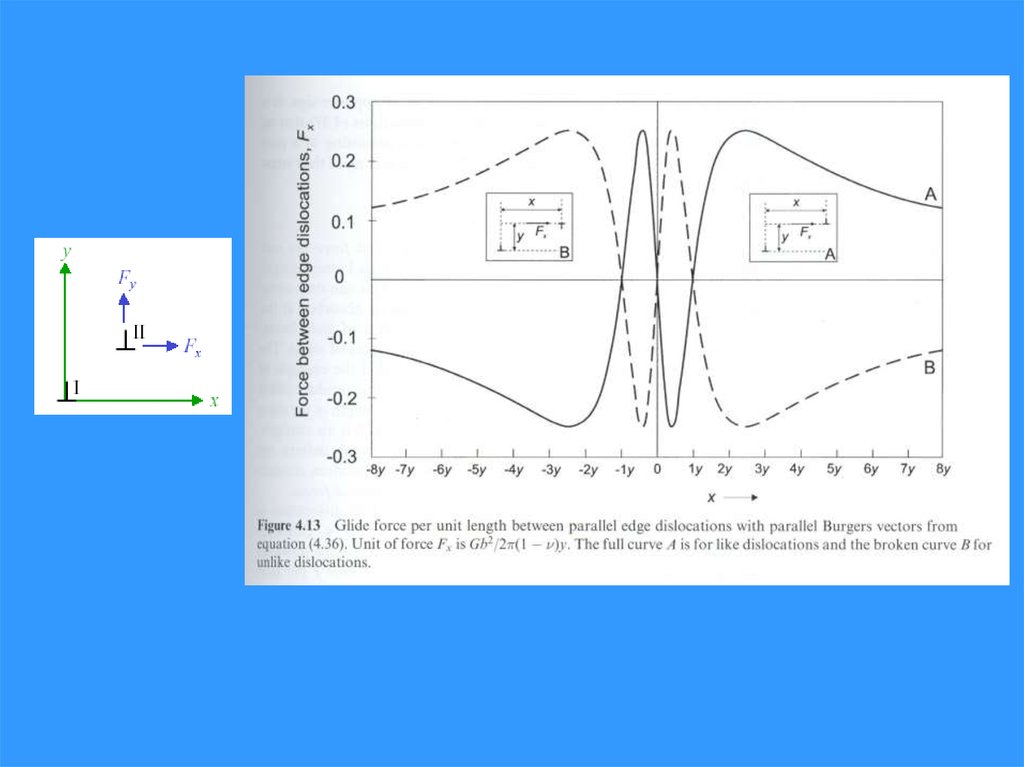
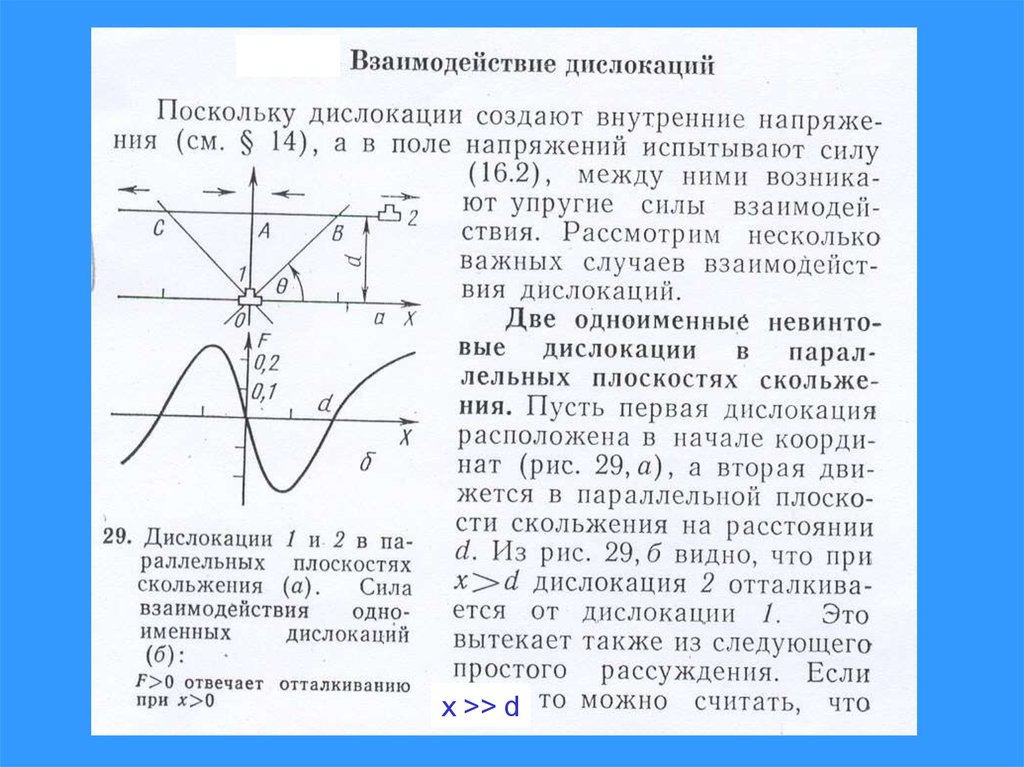
28. Взаимодействие двух параллельных краевых дислокаций
29. Вычисление сил взаимодействий
30.
31.
32.
x >> d33.
34.
Стабильные конфигурации краевых дислокацийСтабильные дипольные
конфигурации для
дислокаций противоположного знака
Стабильная
конфигурация
для дислокаций
одного знака
35.
36.
Почему дислокации не являютсятермодинамически равновесными
дефектами решетки?
b
b
Вектора b и определяют
плоскость скольжения
37.
Оценки упругой энергии дислокацииПри обычных значениях плотности дислокаций
=107 см-2, среднее
расстояние между ними составляет R -1/2 3.10-4 см, что дает
для
и
10
полн /L
=
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
-4 эрг/см
4.10
/L
=
полн
Что в пересчете на одну связь дает:
Ebond
= 4.10 -4 эрг/см x 2.10 -8 см
= 8.10-12 эрг
5 эв
38.
Расчет энтропии дислокационной линии«траектория» дислокационной
линии в плоскости скольжения
Легко вычислить общее число путей длины N :
если каждый узел решетки имеет z соседей,
то число различных возможностей на каждом
шаге есть z-1, и общее число путей равно
= N = (z - 1)N
(сумма статистических весов всех
конфигураций, возможных в системе).
Энтропия S
определяется всеми возможными конформациями
цепи, которые начинаются в начале координат и заканчиваются за N
шагов:
S = kBln = kBNln(z-1)
Двумерный случай, D=2, z = 4:
S = kBNln3
39.
В случае дислокации, состоящей из N звеньев, ее свободнуюэнергию можно записать в виде:
F = NE - TS = NE – kBTNln3
или в пересчете на одну связь:
F/N = E – kBTln3
T Tmelt
kB T = 1.4 10-16 эрг/К x 1200 К =1.6 10-13 эрг 10-1 эв
E = Ebond 5 эв .
E >> kB T
Таким образом, прирост энтропии благодаря создаваемому
дислокациями беспорядку, недостаточен, чтобы компенсировать
рост энергии дислокационной линии.
40.
41.
Таким образом свободная энергия системыможет быть минимизирована только если все
дислокации удалены из кристалла.
Термодинамически равновесные дислокации не
могут существовать в кристалле.
Дислокации, в отличие от точечных дефектов,
являются линейными дефектами решетки. Это
топологическое отличие проявляется при подсчете
числа состояний и энтропии дислокаций.
42.
Равновесная концентрация точечныхдефектов
= CNn = N!/n!(N-n)!
c = n/N e E/ kT





































 Физика
Физика








