Строение и размеры объектов Вселенной

1.

Белорусский государственный университет
Физический факультет
Кафедра атомной физики и физической информатики
Астрономия
Курс лекций
Автор: доктор физико-математических наук профессор
Клищенко Анатолий Петрович
Лектор: доцент, кандидат физико-математических наук
Хвалей Сергей Владимирович

2. Введение

АСТРОНОМИЯ – наука о физическом строении, движении,
происхождении и эволюции небесных тех, их систем,
Вселенной в целом.
Объекты Астрономии – Солнце, звезды, планеты и их спутники,
метеорные тела, туманности, звездные скопления, звездные
системы и вся Вселенная.
Новые объекты – пульсары, квазары, барстеры, космические
лучи, «реликтовое» излучение, «черные» и «белые» дыры,
поиски внеземных цивилизаций.

3.

ЭТАПЫ РАЗВИТИЯ АСТРОНОМИИ
3000 лет до н.э.- Возникновение астрономии. Первый этап
строительства Стоунхенджа
2500 лет до н.э. - Выделение созвездий (шумеро-аннадская
цивилизация)
4000 лет назад - Возникновение китайской и египетской астрономии
Греческая астрономия
585 год до н.э. - Предсказание солнечного затмения Филесом
Милетским
432 год до н.э. - Открытие Метонова цикла
120 год до н.э. - Гиппарх (прецессия, видимое движение тел)
140 год н.э.
- Геоцентризм Птолемея (публикация «Альмагеста»
Арабская астрономия
850 год
- аль-Баттани изучает и проверяет открытия греков
1038 год
- аль-Хасен изучает атмосферную рефракцию
15 век
- Улукбек строит обсерваторию, создает
оригинальный звездный каталог
1542 год
1576 год
1608 год
1609 год
- Коперник публикует трактат «Об обращении
небесных тел»
- Строительство обсерватории Тихо Браге в Дании
- Изобретение телескопа Галилеем
- Публикация первых двух законов Кеплера

4.

1676 год
1687 год
1781 год
1809 год
1817 год
1842 год
1846 год
1905 год
1915 год
1930 год
1945 год
1957 год
1959 год
1960 год
1961 год
- Карл II основал Гринвичскую обсерваторию
- Публикация «Математических начал натуральной
философии» Ньютона
- Уильям Гершель открывает планету Уран
- Публикация Гауссом «Теории движения небесных
тел»
- Фраунгофер открывает темные линии в спектре
Солнца
- Первый дагерротип Солнца
- Открытие Нептуна Адамсом и Лаверье
- Специальная теория относительности Эйнштейна
- Общая теория относительности Эйнштейна
- Томбо открывает Плутон
- Развитие радиоастрономии
- Запуск первого искусственного спутника Земли
- Первые фотографии обратной стороны Луна (КА
«Луна-3»)
- Открытие квазаров
- Первый космический полет Юрия Гагарина на
космическом корабле «Восток»

5.

1961 год
1963 год
1966 год
1967 год
1969 год
1971 год
1976 год
1977 год
1972 1981 годы
1986 год
1989 год
1990 год
- Полет «Меринера-2» к Венере
- Первый полет женщины-космонавта Валентины
Терешковой
- Первая мягкая посадка на Луну «Луна-9»
- Открытие первого пульсара
- Нейл Армстронг – первый человек, ступивший на
поверхности Луна (программа «Апполон»)
- «Меринер-9» - первый искусственный спутник Марса
- Спускаемый модуль «Викинг-1» садится на
поверхности Марса
- Ввод в строй 6-метрового телескопа Зеленгугской
обсерватории (СССР, Краснодарский край)
- Запуск КА «Пионер-10, -11», «Викинг-1, -2»,
«Вояджер-1, -2» для исследования внутренних и
внешних внутренних и внешних областей Солнечной
системы
- КА «Вега» и «Джотто» встречаются с кометой
Галлея. Запуск космической станции «Мир»
- «Вояджер-2» достигает Нептуна
- Вывод на орбиту космического телескопа Хаббл

6. Разделы астрономии

Астрометрия – разрабатывает теоретические методы, технику
измерений на небесной сфере, способы обработки наблюдений.
В ведении Астрометрии – служба времени, календарь, определение
координат пунктов на Земле
а) Сферическая Астрометрия – разрабатывает математические методы
определения положения и движения небесных тел, а также системы
счета времени.
б) Практическая Астрометрия – разрабатывает способы наблюдений,
методы их обработки, теорию астрономических приборов.
Небесная механика – изучает пространственное движение тел и их
систем под действием сил тяготения и другой природы. Определяет
элементы орбит по данным наблюдений и вычисляет видимые
положения небесных тел.
Астрофизика – изучает физическое состояние и процессы на
поверхности и внутри небесных тел.
а) Практическая Астрофизика – разрабатывает способы наблюдений
небесных тел, их обработку.
б) Теоретическая Астрофизика – объясняет наблюдаемые явления,
процессы на основе физических законов.

7.

Звездная Астрономия – изучает движение,
распределение в пространстве звезд, туманностей,
звездных систем, их структуру, эволюцию (раздел –
внегалактическая астрономия).
Космогония – занимается проблемами происхождения
и эволюции небесных тел и их систем,
происхождением Солнечной системы.
Космология – изучает Вселенную как единое целое,
выявляет структуру, ее эволюцию и происхождение ее
структурных единиц.
а) экспериментальная основа – астрофизика и звездная
астрономия.
б) теоретическая – ОТО, физика элементарных частиц,
квантовая механика, электродинамика.

8. Строение и размеры объектов Вселенной

Земля
Земля – Луна
Земля – Солнце
Солнечная система
Солнце – Проксима ( CenC)
Галактика (Млечный Путь)
Галактика – Б.Магелланого Облако
Скопление звездных систем
Сверх Галактика (1015 звезд)
Метагалактика
dср = 12756 км
l = 384400 км
L = 149600000 км
d =10 млрд.км
L = 1,32 пк =
40,7352 1012 км
d = 30000 пк
L = 50000 пк
d = 3 20 Мпк
d = 50 Мпк
d= 60 103 Мпк

9. Количество небесных объектов

Галактика
Звездные системы (галактики)ё
Число галактик
1012 звезд
109 1012 звезд
~ 1012
Предельная яркость наблюдаемых небесных
объектов
(в звездных величинах)
Невооруженным глазом
Глазом с помощью телескопа
Телескоп с фотографической регистрацией
Телескоп с фотоэлектрической регистрацией
+6m
17 19m
22 24m
27 29m

10. Астрономия и деятельность человека

Геодезия и картография.
Геологическая разведка полезных
ископаемых.
Астрономическая служба времени.
Выбор орбит ИСЗ средствами Н.М.
Охрана природы, космонавтов от
излучения.
Космическая технология.

11. Литература

Основная:
Бакулин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии.
Учебник. – М.: Наука, 1977. – 544 с.
Воронцов-Вельяминов Б.А. и др. Методика преподавания астрономии
в средней школе: Пособие для учителя. – М.: Просвещение, 1985. –
240 с.
Воронцов-Вельяминов Б.А. Сборник задач и практических
упражнений по астрономии. – М.: Наука, 1977. – 272 с.
Клищенко А.П., Шупляк В.И. Астрономия: Учебное пособие. – М.:
Новое знание, 2004. – 224 с.
Кононович Э.В., Мороз В.И. Общий курс астрономии: Учебное
пособие. – М.: Едиториал УРСС, 2001. – 544 с.
Левитан Е.П. Дидактика астрономии. – М.: Едиториал УРСС, 2004. –
296 с.
Мартынов Д. Я., Липунов В.М. Сборник задач по астрофизике. – М.:
Наука, 1988. – 125 с.
Мартынов Д.Я. Курс общей астрофизики: Учебник. – М.: Наука, 1988.
– 640 с.
Соболев В.В. Курс теоретической астрофизики. – М.: Наука, 1985. –
326 с.

12.

Дополнительная
Агекян Т.А. Звезды, галактики, Метагалактика. – М.: Наука, 1981. – 416 с.
Волынский Б.А. Астрономия: (Учебное пособие для естеств.–геогр. фак. пед. ин-тов). /Под
ред. проф. Р.В.Куницкого. – М.: Просвещение, 1971. – 208 с.
Горбацкий В.Г. Введение в физику галактик и скоплений галактик. – М.: Наука, 1986. – 253 с.
Гуревич Л.Э., Чернин А.Д. Происхождение галактик и звезд. – М.: Наука, 1987. – 190 с.
Дагаев М.М. Лабораторный практикум по курсу общей астрономии: (Для пед. ин-тов). – М.:
Высшая школа, 1972. – 284 с.
Дагаев М.М. Сборник задач по астрономии: (Для физ.–мат. фак. пед. ин-тов). – М.:
Просвещение, 1980. – 128 с.
Дагаев М.М., Демин В.Г., Климишин И.А., Чаругин В.М. Астрономия: (Учебное пособие для
физ.–мат. фак. пед. ин-тов). – М.: Просвещение, 1983. – 384 с.
Данлоп С. Азбука звездного неба: Пер. с англ. – М.: Мир, 1990. – 238 с.
Климишин И.А. Астрономия наших дней. – М.: Наука, 1986. – 560 с.
Климишин И.А. Элементарная астрономия. – М.: Наука, 1991. – 462 с.
Курышев В.И. Практикум по астрономии: (Учебное пособие для физ. и мат. спец. пед. интов). – М.: Просвещение, 1986. – 141 с.
Масевич А.Г., Тутуков А.В. Эволюция звезд: теория и наблюдения. – М.: Наука, 1988. – 280 с.
Монтенбрук О., Пфлегер Т. Астрономия на персональном компьютере (+СD). – Изд-во Питер.
– 2002. – 320 с.
Москаленко Е.И. Методы внеатмосферной астрономии: Учебное пособие. – М.: Наука, 1984.
– 280 с.
Мур П. Астрономия с Патриком Муром: Пер. с англ. – М.: ФАИР-ПРЕСС, 1999. – 368 с.
Оксфордская иллюстрированная энциклопедия. В 9 тт. Т. 8. Вселенная: Пер. с англ. – М.:
"Издательский дом ИНФРА-М", изд-во "Весь Мир", 2000. – 204 с.
Сурдин В.Г. Астрономические олимпиады. – М.: МГУ, 1995. – 320 с.
Уокер Г. Астрономические наблюдения: Пер. с англ. – М.: Мир, 1990. – 352 с.
Щеглов П.В. Проблемы оптической астрономии. – М.: Наука, 1986. – 271 с.

13.

14.

N север
NE северо - восток
S юг
SE юго – восток
A
азимут
или (AR) прямое восхождение
склонение
эклиптическая, а также
географическая долгота
E восток
NW
северо – запад
W запад
SW
юго - запад
z
a год
d сутки
l или l
h, m, s час, минута, секунда времени
, ,
градус, минута, секунда дуги
t часовой угол светила
Vr
s звездное время
h
эклиптическая широта
географическая широта
зенитное расстояние
собственное движение
галактическая долгота
b
галактическая широта
годичный параллакс
лучевая скорость
высота светила над
горизонтом
T солнечное время
T звездный год
p
полярное расстояние
угол между эклиптикой и небесным экватором (между экватором Земли
и плоскостью ее орбиты)

15.

ЗНАКИ ЗОДИАКА
Arles (Овен), а также точка весеннего равноденствия
в созвездии Рыб
Libra (Весы), а также точка осеннего равноденствия
в созвездии Девы
Taurus (Телец)
Scorpius (Скорпион)
Gemini (Близнецы)
Sagittarius (Стрелец)
Cancer (Рак), а также точка летнего
солнцестояния в созвездии Тельца (с 1990 г.)
Capricornus (Козерог), а также точка зимнего
солнцестояния в созвездии Стрельца
Leo (Лев)
Aquarius (Водолей)
Virgo (Дева)
Pisces (Рыбы)

16.

Глава I СФЕРИЧЕСКАЯ АСТРОНОМИЯ
Карта звездного неба

17.

Характеристики сферы: FG, HK –
большие круги сферы (радиуса
R), ab – малый круг сферы
(радиуса r), - центральный
угол в плоскости большого
круга,
угол
между
плоскостями больших кругов
Вид небесной сферы для
наблюдателя, находящегося
на поверхности Земли на
широте (точка О)

18.

Небесный
меридиан
Z
Ось мира
Q
P
i=90 -
E
hp=
S
0
N
i
Истинный
горизонт
Полуденная
линия
w
i
P
Q
Z
Основные элементы
небесной сферы

19.

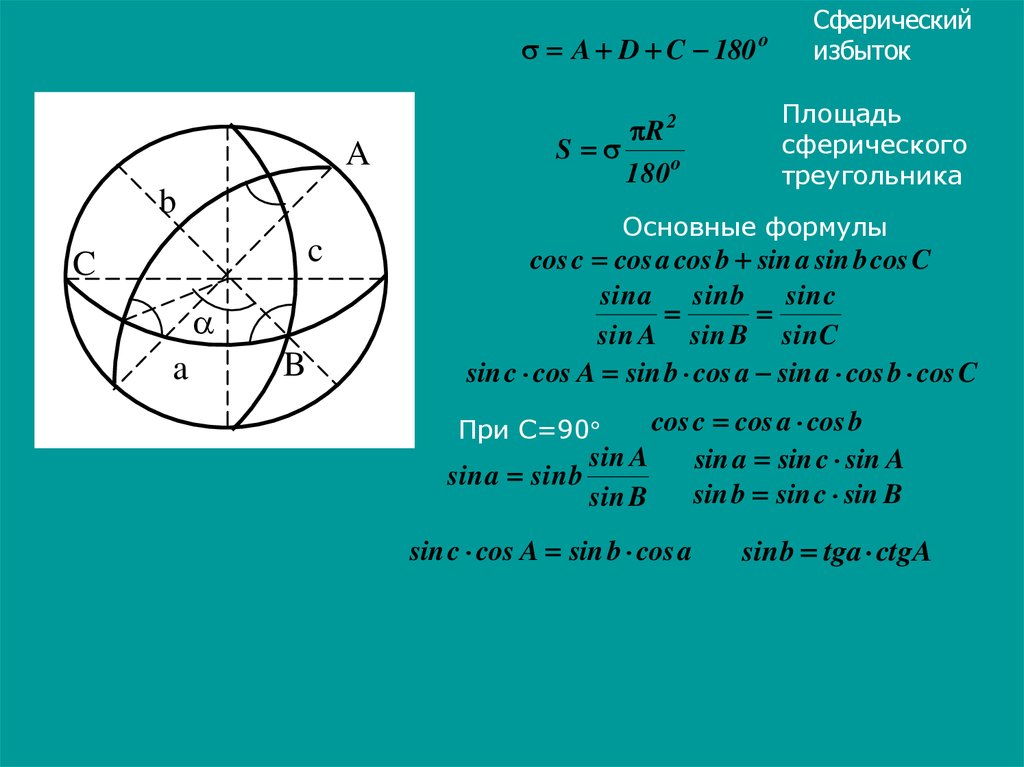
A D C 180
A
R 2
S
180o
b
c
C
a
B
o
Сферический
избыток
Площадь
сферического
треугольника
Основные формулы
cos c cos a cos b sin a sin b cos C
sin a sin b sin c
sin A sin B sin C
sin c cos A sin b cos a sin a cos b cos C
cos c cos a cos b
sin A
sin a sin c sin A
sin a sin b
sin b sin c sin B
sin B
При С=90
sin c cos A sin b cos a
sinb tga ctgA

20.

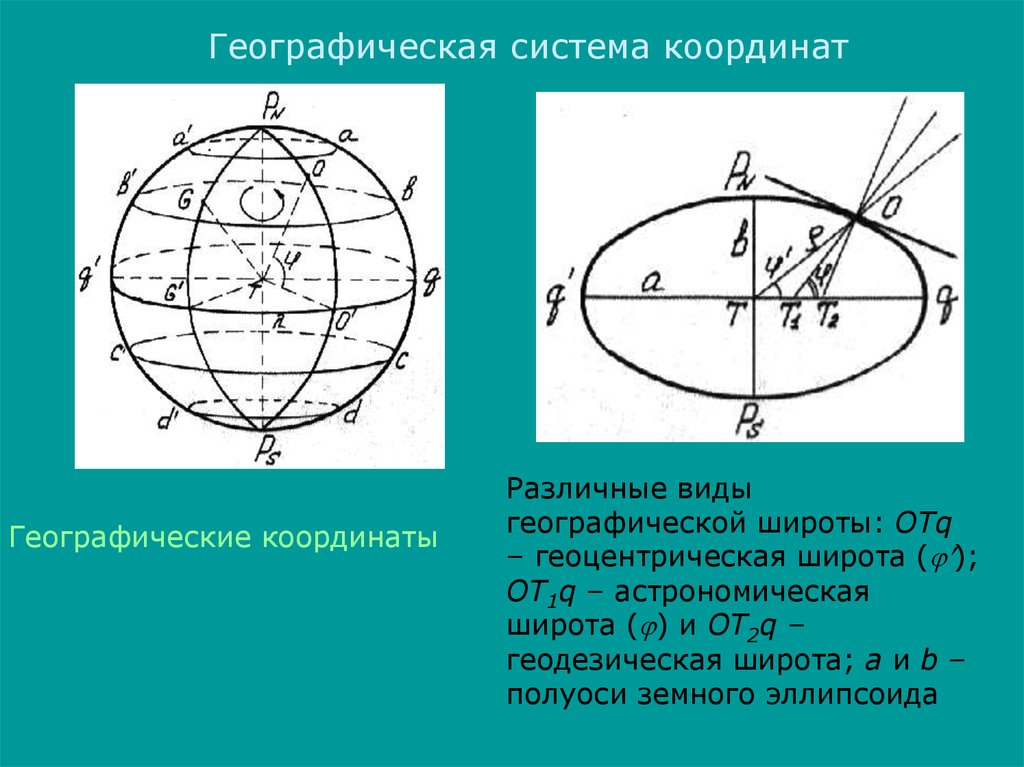
Географическая система координат
Географические координаты
Различные виды
географической широты: ОТq
– геоцентрическая широта ( );
ОТ1q – астрономическая
широта ( ) и ОТ2q –
геодезическая широта; а и b –
полуоси земного эллипсоида

21.

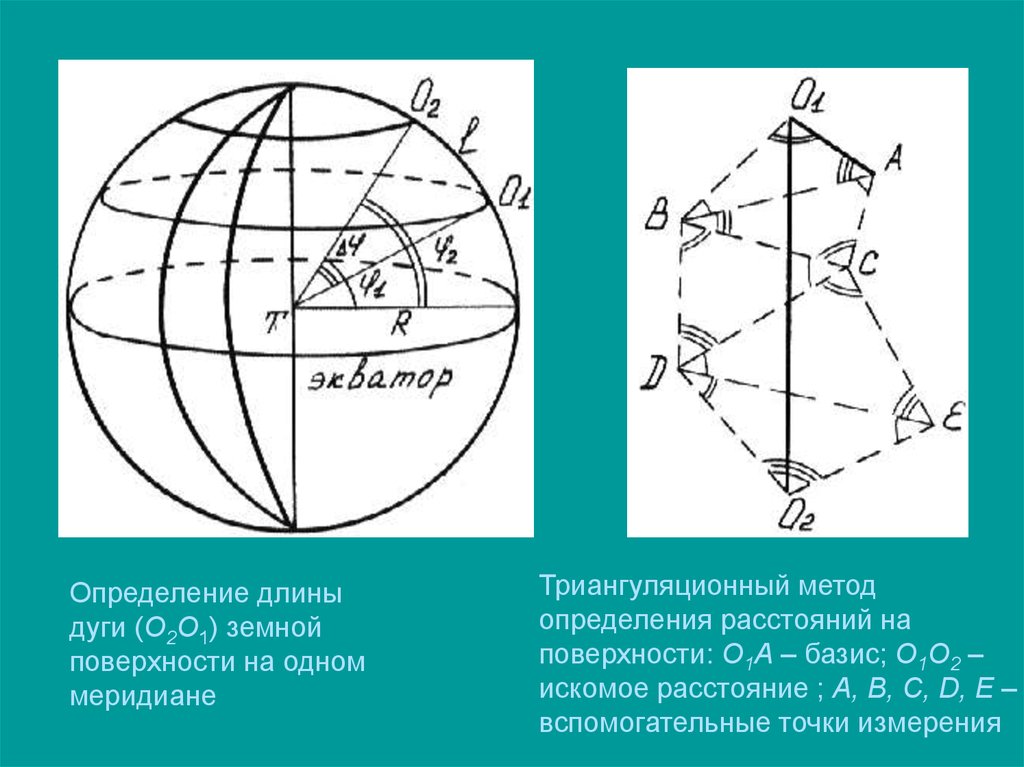
Определение длины
дуги (О2О1) земной
поверхности на одном
меридиане
Триангуляционный метод
определения расстояний на
поверхности: О1А – базис; О1О2 –
искомое расстояние ; А, В, С, D, E –
вспомогательные точки измерения

22.

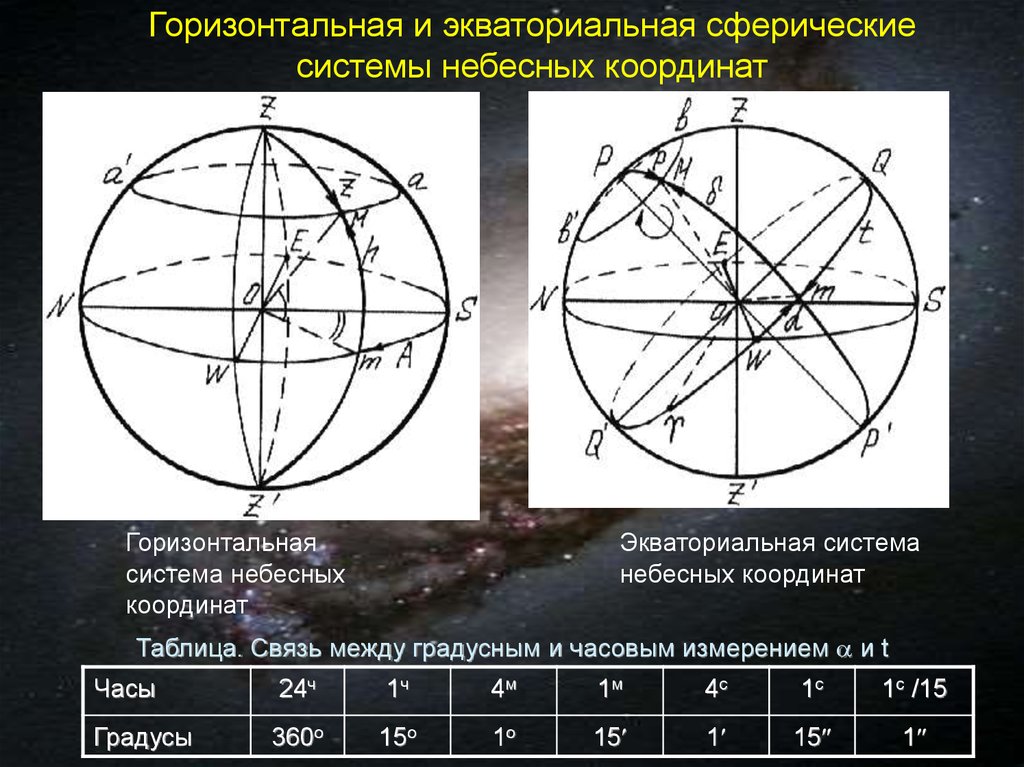
Горизонтальная и экваториальная сферические
системы небесных координат
Горизонтальная
система небесных
координат
Экваториальная система
небесных координат
Таблица. Связь между градусным и часовым измерением и t
Часы
24ч
1ч
4м
1м
4с
1с
1с /15
Градусы
360о
15о
1о
15
1
15
1

23.

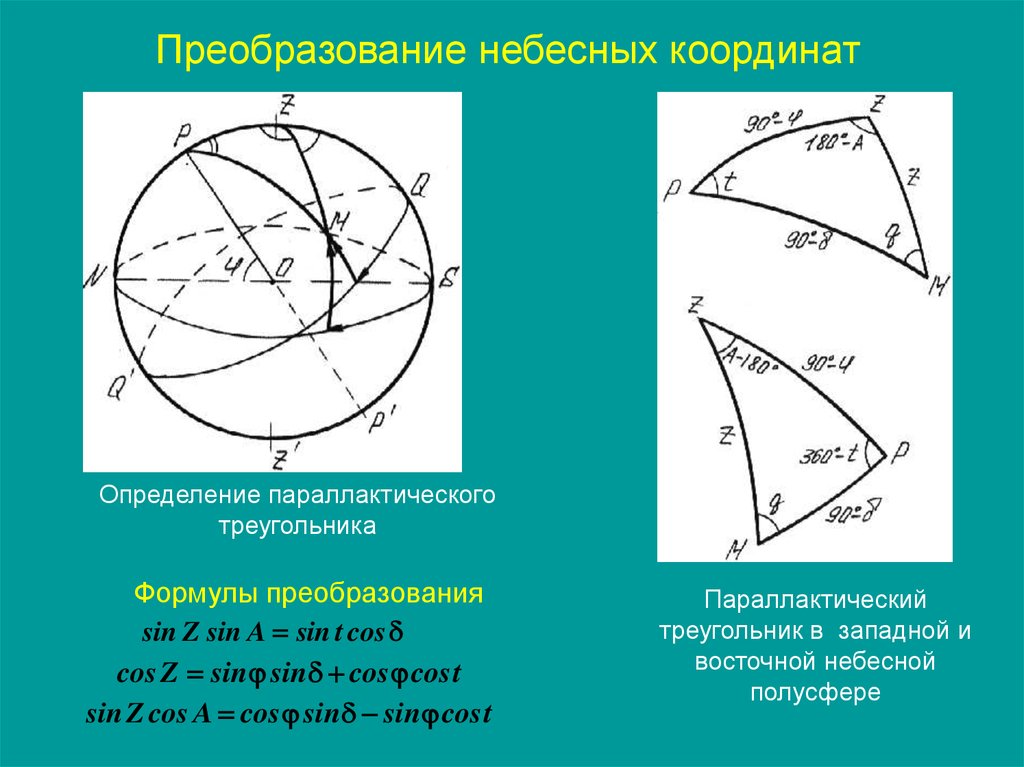
Преобразование небесных координат
Определение параллактического
треугольника
Формулы преобразования
sin Z sin A sin t cos
cos Z sin sin cos cos t
sin Z cos A cos sin sin cos t
Параллактический
треугольник в западной и
восточной небесной
полусфере

24.

Z
P
N
S
P
Z
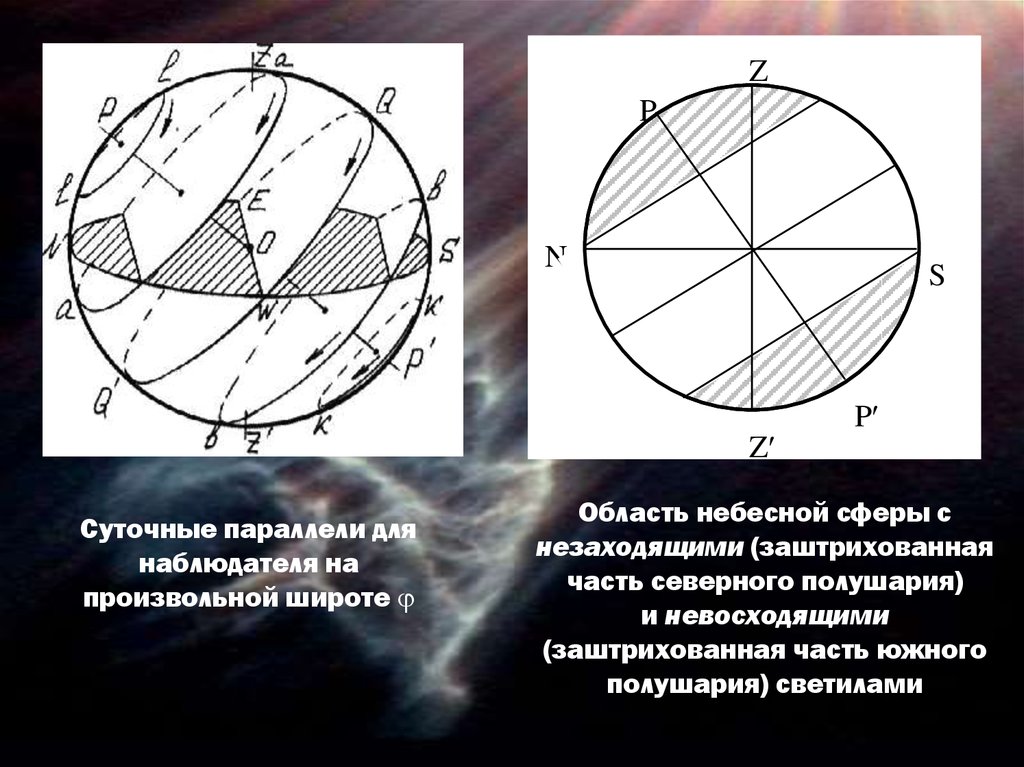
Суточные параллели для
наблюдателя на
произвольной широте
Область небесной сферы с
незаходящими (заштрихованная
часть северного полушария)
и невосходящими
(заштрихованная часть южного
полушария) светилами

25.

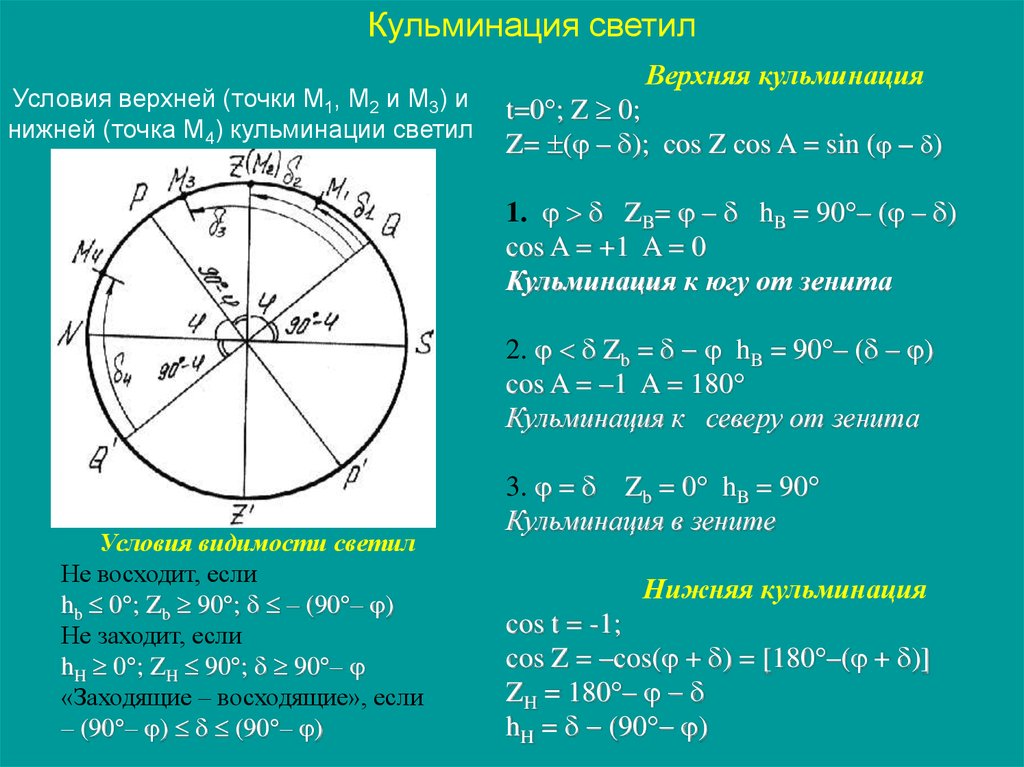
Кульминация светил
Условия верхней (точки М1, М2 и М3) и
нижней (точка М4) кульминации светил
Верхняя кульминация
t=0 ; Z 0;
Z= ( – ); cos Z cos A = sin ( – )
1. ZB= – hB = 90 – ( – )
cos A = +1 A = 0
Кульминация к югу от зенита
2. Zb = hB = 90 – ( – )
cos A = –1 A = 180
Кульминация к северу от зенита
Условия видимости светил
Не восходит, если
hb 0 ; Zb 90 ; – (90 – )
Не заходит, если
hH 0 ; ZH 90 ; 90 –
«Заходящие – восходящие», если
– (90 – ) (90 – )
3. = Zb = 0 hB = 90
Кульминация в зените
Нижняя кульминация
cos t = -1;
cos Z = –cos( + ) = [180 –( + )]
ZH = 180 –
hH = (90 )

26.

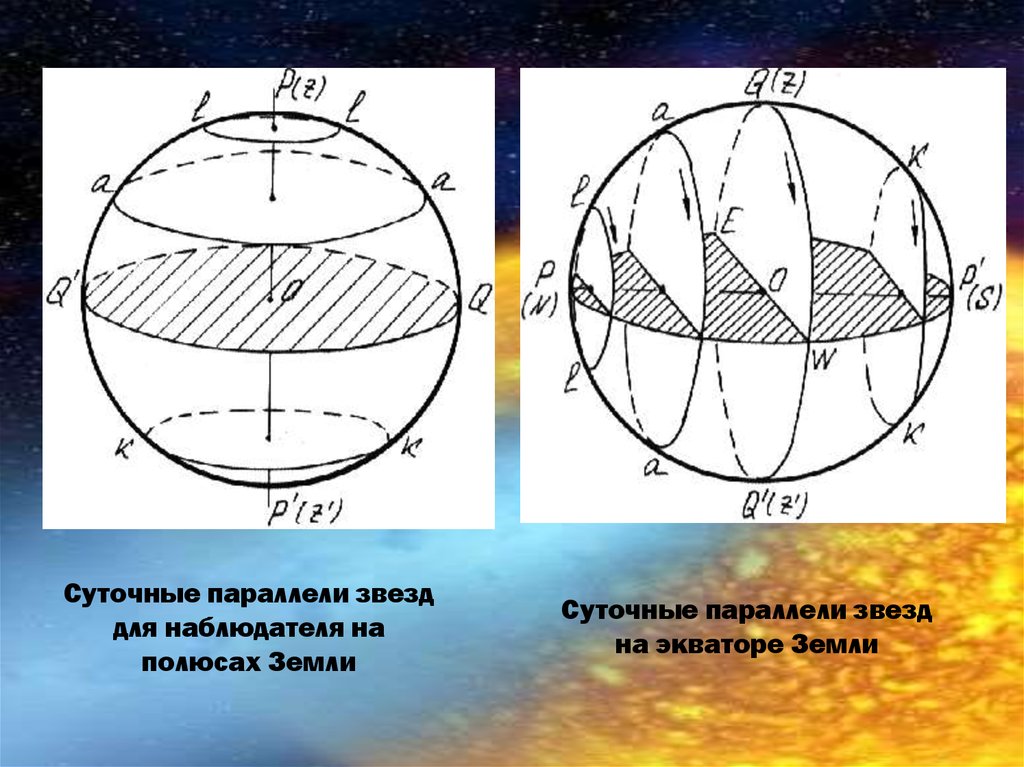
Суточные параллели звезд
для наблюдателя на
полюсах Земли
Суточные параллели звезд
на экваторе Земли

27.

Видимое движение Солнца, его причины и следствия
P
П
( )
Q
Q
( )
P
П
Истинный
горизонт
Основные линии и точки
небесной сферы, связанные с
эклиптикой
Схема, поясняющая метод
определения абсолютных
координат Солнца ʘ и ʘ:
QQ - линия небесного
экватора, - линия эклиптики
= - ZВ
sin =tg ctg ε

28.

Эклиптическая система координат

29.

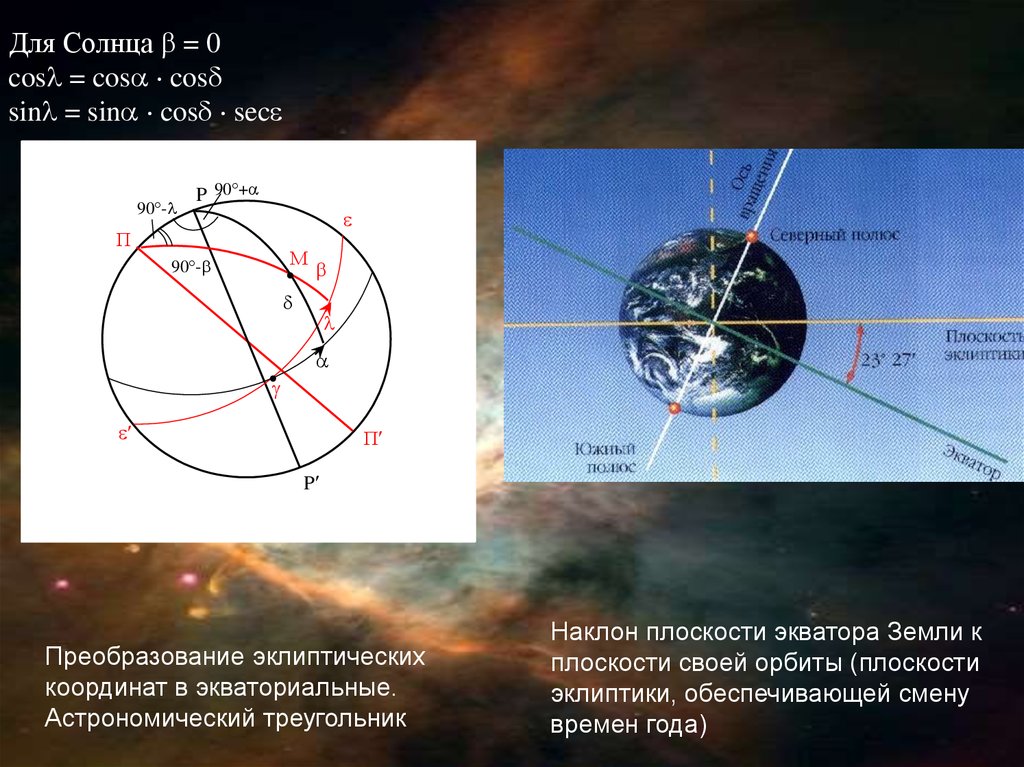
Для Солнца = 0
cos = cos cos
sin = sin cos sec
90 -
P 90 +
П
М
90 -
П
P
Преобразование эклиптических
координат в экваториальные.
Астрономический треугольник
Наклон плоскости экватора Земли к
плоскости своей орбиты (плоскости
эклиптики, обеспечивающей смену
времен года)

30.

Смена времен года на планете Земля
Т = 365,2564 = 365Д6Ч09М10С
Т = 365Д5Ч48М46С
nср = 360 /Т = 59 /день
Летом n = 59 /день
Зимой n = 61 /день
Начало года: = 280

31.

Климатические (тепловые) пояса Земли
P, Северный полюс Земли ( = 90 )
Северный полярный круг ( = 66 33 )
Северный тропик
(Рака, = 23 27 )
Экватор ( = 0 )
Южный тропик
(Козерога, = - 23 27 )
Южный полярный круг ( = - 66 33 )
P, Южный полюс земли ( = -90 )

32.

Измерение времени
Звездное время
B
A
P
Связь всемирного So и
местного S звездного
времени
D
E
F
S = So + ;
So – звездное время Гринвича
S = t - звездное время, t – часовой угол точки .
S = + t, где t – часовой угол звезды с прямым
восхождением .

33.

Истинное и среднее солнечное время
C
Небесный
меридиан
1
Если t = 0ч, то Т = 12ч – истинный полдень
Т = Т - Т = 3м56с,56 – разница между
солнечными и звездными сутками
O
Т = t + 12Ч – истинное солнечное время
O
O
Орбита
Земли
Схема, поясняющая отличие
звездных суток от истинных
солнечных суток

34.

Среднее солнечное время. Уравнение времени
Т = <Т > = 24Ч; 1Ч=60М; 1М=60С
Q
= Т - Т - уравнение времени
Q
a)
t = S - T = To +
To – всемирное время, - долгота
местности
Q
Q
Т - среднее солнечное время
б)
Характер изменения и в точках
равноденствия (1) и солнцестояния (2)

35.

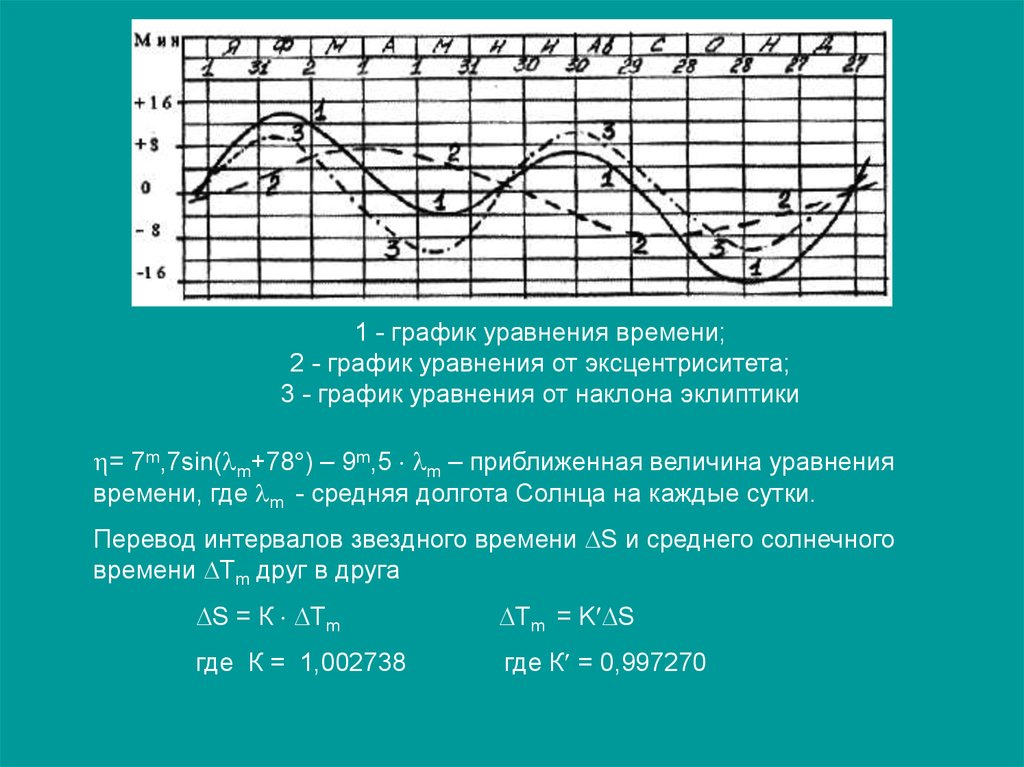
1 - график уравнения времени;
2 - график уравнения от эксцентриситета;
3 - график уравнения от наклона эклиптики
= 7m,7sin( m+78 ) – 9m,5 m – приближенная величина уравнения
времени, где m - средняя долгота Солнца на каждые сутки.
Перевод интервалов звездного времени S и среднего солнечного
времени Тm друг в друга
S = К Тm
Тm = K S
где К = 1,002738
где К = 0,997270

36. Системы счета времени

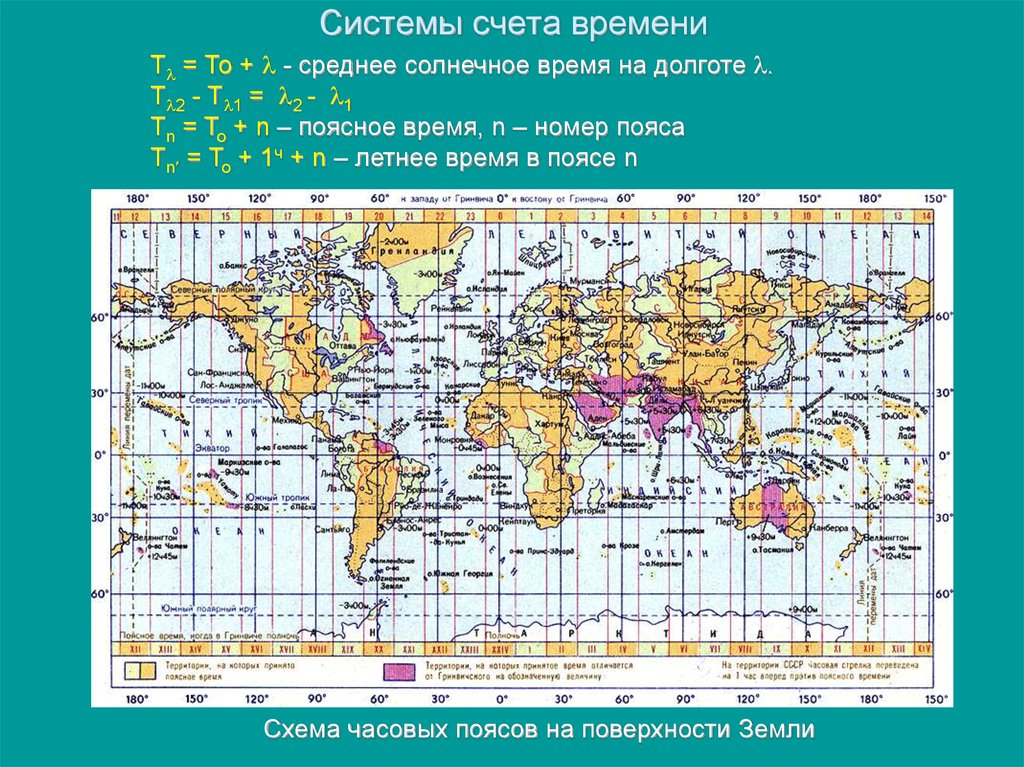
Т = То + - среднее солнечное время на долготе .
Т 2 - Т 1 = 2 - 1
Тn = To + n – поясное время, n – номер пояса
Тn = To + 1ч + n – летнее время в поясе n
Схема часовых поясов на поверхности Земли

37. Эфемеридное время

Положения объектов солнечной системы, вычисленные на основании
теории тяготения, относятся по времени, которое является независимой
переменной дифференциальных уравнений движения небесных тел. Это
время считается равномерным и называется эфемеридным (Тэф).
Если бы Земля вращалась вокруг своей оси также равномерно, то
наблюдаемые и вычисленные координаты Солнца, Луны и планет для 0ч
всемирного и 0ч эфемеридного времени совпали.
Однако, как показывают наблюдения, угловая скорость Земли
непостоянна из-за вековых и скачкообразных периодических и сезонных
изменений. В результате вековых изменений продолжительность одного
оборота Земли увеличилась за последние 2000 лет на 0с,0023 за столетие
(за последние 250 лет это увеличение уменьшилось – около 0с,0014 за
100 лет). Причина этого замедления в действии солнечных и лунных
приливов. В результате сезонных изменений скорость вращения Земли
может отличаться от средней на 0с,001.
Неравномерность вращения Земли приводит к разности наблюдаемых и
вычисленных координат планет, Луны и Солнца, причем она больше,
чем больше среднее суточное движение светила n = 360o/T и зависит от
разности между эфемеридным Тэф и всемирным временем То. Поскольку
n имеют Луна, Меркурий, Венера и Солнце, то для этих объектов
следует ожидать различие в координатах вычисленных и наблюдаемых.

38.

Величина Т = Тэф – То вычисляется из сравнения наблюдаемых и
эфемеридных координат Луны (для ее эта величина наибольшая) по
формуле
Т = +24с,349+72с,318Т + 29с,950Т2 + 1,821В, где Т – время в юлианских
столетиях, отсчитанное от момента 1900,0 12ч эфемеридного времени в
Гринвиче, В – флуктуация долготы Луны.
Разность Т в 1900 году была близка к нулю.
В настоящий момент эфемеридное время на 55 сек опережает всемирное.
За последнее столетие изменился подход к определению эталона
времени. В связи с использованием с 1952 года эфемеридного времени
было введено новое определение секунды. До 1956 года секунда
определялась как 1/86400 доля солнечных суток. В октябре 1956 года
Международное Бюро мер и весов установило 1 секунду как
1/31556425,9747 долю тропического года, продолжительность которого
в системе эфемеридного времени в 1900 г. равнялась 365, 2421988
средних солнечных суток.
Создание атомных и молекулярных эталонов привело к созданию в 1972
г. атомного времени, которое определяется атомными процессами и в
настоящее время считается наиболее точным.

39.

Календарь
–
это
система
для
фиксирования
начала,
продолжительности и порядка
следования времени года. Все
календари можно разделить на три типа: солнечный, лунный и
солнечно-лунный. В основе первого лежит продолжительность
тропического года (365,2422 дня), лунного – синодический месяц, или
лунация (около 29,5 дней) третьего типа – комбинация лунного месяца
и солнечного года.
При составлении календарного года (календаря) надо учитывать
следующие факторы:
1. Продолжительность календарного года в среднем за несколько лет
должна быть как можно ближе к продолжительности тропического
года, а, следовательно, трудовой деятельности человека.
2. Календарь должен содержать целое число средних солнечных
суток, т.к. неудобно начинать один год ночью, другой утром и т.д.
У большинства народов сначала был принят лунный календарь, в
котором основным интервалом был месяц, а не год, и были
предложены различные системы, чтобы согласовать его с циклом
смены времен года. Например, для вавилонян начало нового месяца
было появление на западном небе нарождающейся Луны, причем
началом суток был момент восхода Солнца. Средняя длина этих
месяцев была равны синодическому месяцу и нормальный год имел 12
месяцев или около 354 суток. Для того, чтобы поддерживать
соответствие календаря временам года по мере необходимости
вставляли дополнительный месяц (проводили интерполяцию).

40. Календарь (К)

К – система счета длительных
промежутков времени
1.
Солнечный - основа – тропический
год
2.
Лунный – основа – синодический
месяц
3.
Солнечно-лунный – сочетание этих
периодов
К учитывает:
1.
Продолжительность К года в
среднем должна совпадать с
продолжительностью
тропического Т = 365,2422 = 365д5ч48м46с
2.
Календарь должен содержать целое
число суток
Юлианский К - (3 х 365 + 1 366) / 4 = 365,25
Т = Т - Тю = 0,0078 сут. (1 сутки за 128 лет)

41.

Основу юлианского календаря, который был распространен в Российской
империи, а затем и в Советском Союзе, а, значит, и в Беларуси, вплоть до
20-х годов 20-го века составил лунный календарь, разработанный
александрийским астрономом Созигеном и введенным в Римской империи
Юлием Цезарем в 46 г. до н.э., что очевидно из его разделения на 12
месяцев. Однако месяцы в нем не соответствуют лунациям, поскольку в
них были добавлены дни, чтобы довести продолжительность года до 365
дней. Точное соответствие со средним солнечным годом достигается
путем вставки каждые четыре года високосного года, содержащего еще
один 366 день – 29 февраля.
Таким образом, средняя продолжительность в юлианском календаре за 4
года составляет 365,25 средних солнечных суток. Расхождение
календарного (юлианского) и тропического годов в 0,0078 суток приводит к
тому, что за 400 лет день весеннего равноденствия по календарной дате
будет наступать на 3 дня раньше.
Вплоть до 16-го века большинство стран Европы пользовались юлианским
календарем, когда было обнаружено, что истинное весеннее
равноденствие происходит на 10 суток раньше календарного, относимого к
21 марта. Установление данного календарного дня связано с с правилом
определения
даты
религиозного
весеннего
праздника
Пасхи,
утвержденным Никейским Собором в 325 году н.э., когда день весеннего
равноденствия пришелся на 21 марта по юлианскому календарю. В
соответствии с решением Никейского Собора дата Пасхи определялась
как первое воскресенье после полнолуния после дня весеннего
равноденствия.
.

42.

Григорианский календарь, впервые введенный в 1582 г. папой Григорием XIII и в
настоящее время используемый почти всеми, вытеснил юлианский благодаря
простым модификациям.
Булла Римского папы от 4 октября 1582 года говорила:
1. После 4 октября предписано считать наступление не 5, а 15 октября 1582 года,
что вернуло календарную дату весеннего равноденствия к 21 марта и
ликвидировало разницу в 10 дней, набежавшую со времени Никейского Собора
325 года н.э.
2. Не считать в дальнейшем високосными те года столетия, у которых число сотен
не делится без остатка на 4 (1700, 1800, 1900, 2100 и т.д.)
Вторым пунктом продолжительность календарного года в среднем за 400 лет
устанавливалась равной 365,2425 суток, что отличало календарный год от
тропического всего на 0,0003 суток (одни сутки набегали за 3000 лет).
Григорианский календарь – это в целом церковный календарь, связанный с
установлением даты Пасхи. Как таковой он, прежде всего, был принят в
католических странах, а затем постепенно распространялся и на другие страны.
Новый (григорианский) стиль календаря в Беларуси (тогда в составе СССР) был
введен лишь в 1918 году, когда необходимо было ликвидировать отставание дат
по старому (юлианскому) календарю на 13 суток. Соответствующим Декретом
было предписано считать вместо 1 февраля дату 14 февраля 1918 года
календарным днем (новый стиль).

43. Юлианские даты (J.D.)

Системы летоисчисления больших промежутков времени, а также начала
календарного года также претерпели достаточно большие изменения. Та
из них, которой в настоящее время пользуются большинство стран, идет о
начала христианской эры (с рождества Христова) и была предложена
римским монархом Дионисием Малым в 525 году. Однако начало года в
разных странах было установлено по-разному, а приход к 1 января
осуществился для большинства стран в 18 веке. В России лишь вначале
18 века указом Петра I 1 января был определен как первый день нового
календарного года.
В практике астрономических исследований часто необходимо знать
количество дней между двумя календарными датами. При этом
необходимо учитывать число високосных годов, что может приводить к
ошибке при больших интервалах событий.
Такие расчеты лучше решать при помощи юлианских дней J.D
(юлианского периода), которые считаются от гринвичского полудня
непрерывно с 1 июля 4713 г. до н.э. и обозначают количество суток (с
учетом дробной части суток), прошедших с этого момента. В
астрономических ежегодниках даются целые числа юлианских дней. В
таблице 1.2 даны юлианские даты и количество дней обычного и
високосного года по месяцам.

44. Юлианские даты (J.D.)

Таблица. Юлианские даты
Юлианские даты (J.D – 2400000) на нулевое число каждого года
Годы
2000
2010
2020
2030
2040
0
51544
55197
58849
62502
66154
1
51910
55562
59215
62867
66520
2
52275
55927
59580
63232
66885
3
52640
56293
59945
63598
67250
4
53005
56658
60310
63963
67615
5
53371
57023
60676
64328
67981
6
53736
57388
61041
64693
68346
7
54101
57754
61406
65059
68711
8
54466
58119
61771
65424
69076
9
54832
58484
62137
65789
69442
Количество дней между 0 число года и каждого месяца
янв. фев. март
апр.
май
июнь июль авг. сен. окт. ноя.
обычн.
0
31
59
90
120
151
181 212 243
273 304
висок.
0
31
60
91
121
152
182 213
244 274 365
дек.
365
366
Пользуясь Таблицей, рассчитаем юлианскую дату J.D. для
8 сентября 2010 года (после 15 часов)
J.D = 2400000 + 55197 + 243 + 8 = 2 455 448
Начало счета юлианских дней условно и было предложено в 15 веке
Скалигером как начало периода в 7980 лет, получаемого перемножением
трех интервалов времени – 28 лет (повторение распределения дней
недели по дням года), 19 лет – метонов цикл, 15 лет – период связанных с
налоговой системой у римлян.

45. Основы практической астрономии

Измерение горизонтальных координат светил и определение
положения небесного меридиана
Определение положения
(значение ns на горизонтальном круге УИ)
небесного меридиана
1. sinZ sin A = cos sint
Если А = - А Z – одинаково
n n
ns
2
2. Зная и (широта)
cos A
Универсальный инструмент (УИ)
sin cos Z sin
cos sin Z
ns n A

46.

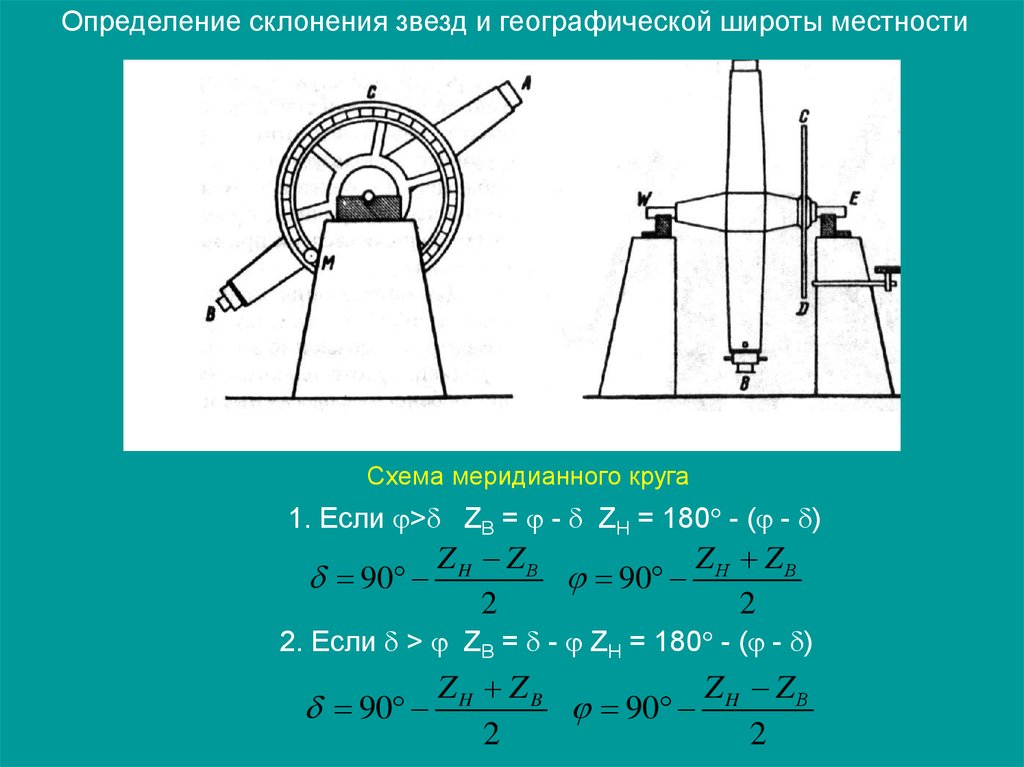
Определение склонения звезд и географической широты местности
Схема меридианного круга
1. Если > ZВ = - ZH = 180 - ( - )
ZH ZВ
ZH ZВ
90
90
2
2
2. Если > ZB = - ZH = 180 - ( - )
ZH ZB
ZH ZВ
90
90
2
2

47. Служба времени

U2 U1
T T
2
1
- ход часов
U2 - U1 – поправка часов
U = T - T - поправка часов
Т – точное время; Т - показания часов
Поправка U в любое время U = U1 + (T2 - T1 )
Поправка звездного времени (звездных часов US = S - S = - S
- склонение звезд, находящейся в верхней кульминации
Для звездных часов USo (Гринвич) = So - S = So – (S – US) = US -
Для солнечных часов UM = TM - T Uo = TM – 2ч - Т
Определение и
определяют через звездное время Солнца S S Z US= - S
U = Us + (S - S ); S = = S + U = S + Us + (S - S )
= + (S - S ) + (S - S )
= S – So = US - USo

48.

Факторы, искажающие видимое положение светил на небе
Рефракция
Z - Z =
= 60 , 25 tgZ (Z 70 )
Влияние рефракции света в
атмосфере
У горизонта
= 35 (tвозд = 0 , = 760 мм рт.
ст.

49.

Суточный параллакс
Ro / sin po
К вопросу о суточном параллаксе Р светила М
и горизонтальном параллаксе Р светила М. R –
К вопросу о годичном параллаксе
радиус Земли, - расстояние от центра Земли
звезды М (С – Солнце, Т – Земля)
до светила
R
R
sinP = sinP sinZ (p = 57 - Луна, Р = 8 ,79 –
sin P sin Z
sin P sin Z
Солнце, Р 1 - у ближайших планет)
Ro
sin Po
sin Po Po sin l
206265
Ro
P
o
Po sinР Р Р sinZ
206265 Если R = Ro = 6378 км (экваториальный радиус
Земли
Р = Ро – горизонтальный экваториальный
параллакс

50. Годичный параллакс

206265
sin
- годичный параллакс
К вопросу о годичном параллаксе звезды М
(С – Солнце, Т – Земля).
- средний радиус орбиты
Земли, равный 1 а.е. =
149600000 км
Таблица основных единиц расстояний, используемых в астрономии, и связь
между ними.
км
а.е.
св.год
1,057 10
парсек
3,2408 10 –
1 км
1
1 а.е.
1,49598 108
1
1 св.год
9,4605 1012
63240
1
0,3066
1 пс
3,0857 1013
206265
3,2616
1
6,6846 10
–9
–13
14
1,5813 10 –5 4,8481 10 –6

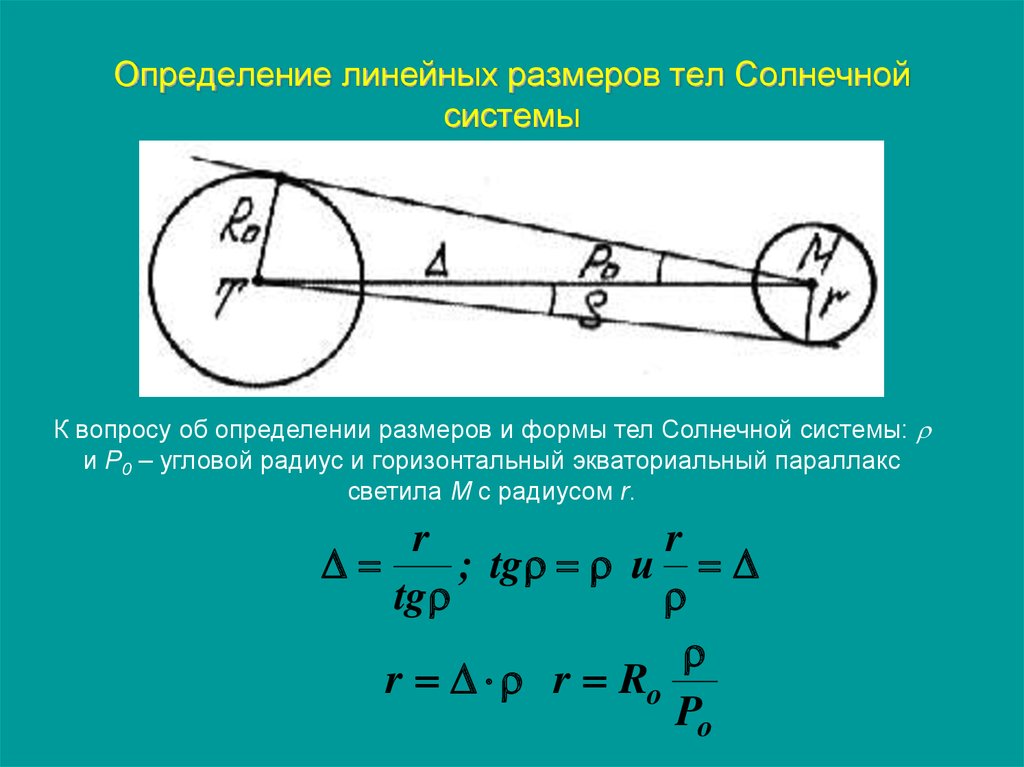
51. Определение линейных размеров тел Солнечной системы

К вопросу об определении размеров и формы тел Солнечной системы:
и Р0 – угловой радиус и горизонтальный экваториальный параллакс
светила М с радиусом r.
r
r
; tg и
tg
r r Ro
Po

52. Восход и заход светил

Часовой угол и азимут восхода tв, Ав и захода tз, Аз светил связаны
формулами
cos Z sin sin
cos t
cos cos
cos
sin A
sin t
sin Z
Если Z - 90 + - р + r ( - рефракция, р – параллакс, r – угловой
радиус светила
sin 35 sin sin
Для звезд
cos t
(r = 0, р = 0)
cos cos
Для Луны
Для Солнца
sin 7 sin sin
cos t
cos cos
sin 51 sin sin
cos t
cos cos
cos t tg tg
(р 0)
(r = 0, p = 0, = 0)

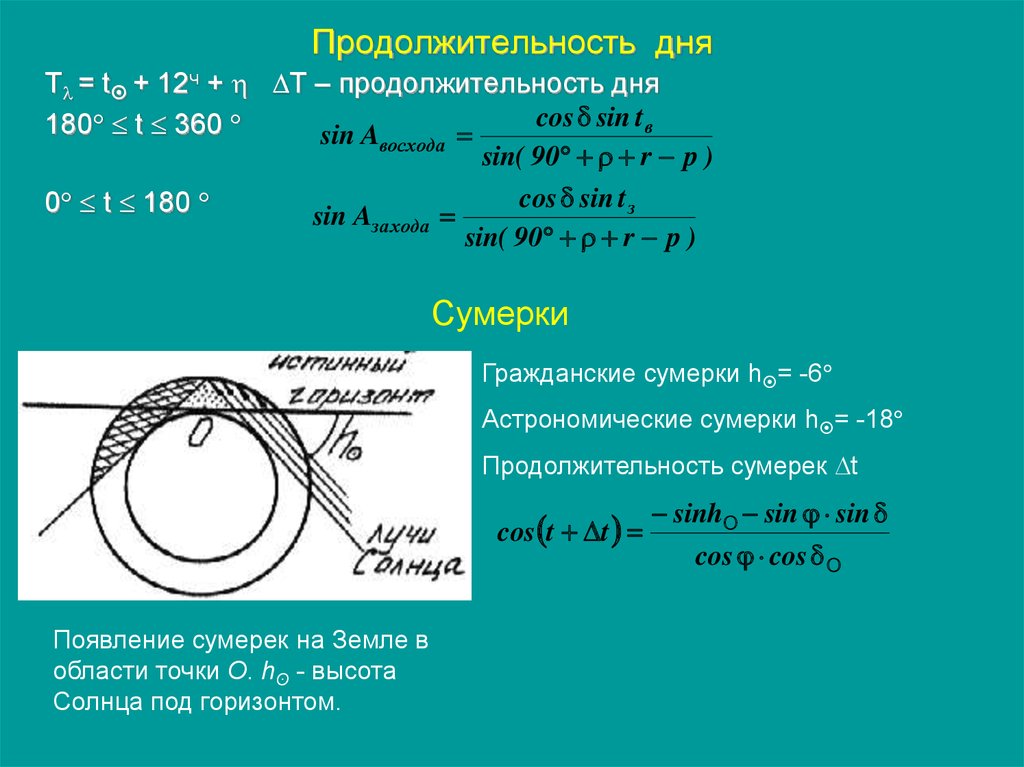
53. Продолжительность дня

T = t + 12ч + Т – продолжительность дня
cos sin t в
180 t 360
sin Aвосхода
sin( 90 r p )
cos sin t з
0 t 180
sin Aзахода
sin( 90 r p )
Сумерки
Гражданские сумерки h = -6
Астрономические сумерки h = -18
Продолжительность сумерек t
cos t t
Появление сумерек на Земле в
области точки О. hʘ - высота
Солнца под горизонтом.
sinh sin sin
cos cos

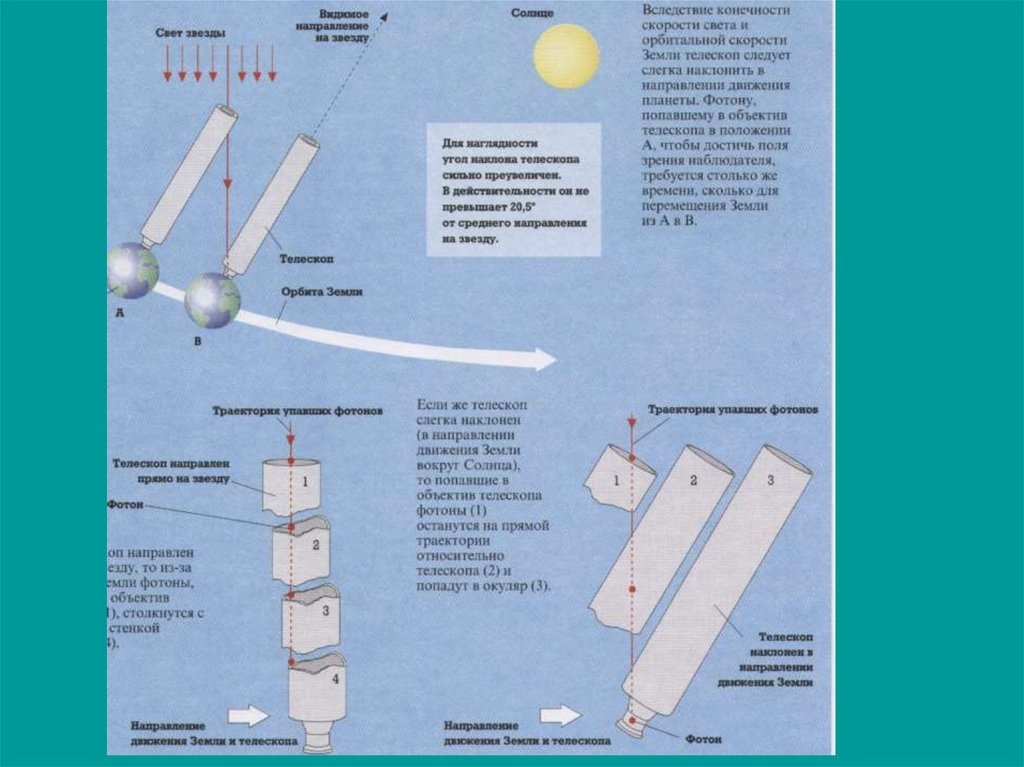
54. Суточная и годичная аберрация

sin v sin
c
v
206265 sin
c
Для суточной аберрации V = vocos , vo – скорость наблюдателя на экваторе,
- широта местности.
v cos
с (суточная аберрация) = o
sin 0 , 315 cos sin
c
0 ,464 км с
0 , 315
Где Кс =
- коэффициент суточной аберрации
5
3 10 км с
Для годичной аберрации vср=29,765км/с и
206265 29 ,765
sin 20 , 496 sin
г (годичная аберрация)
5
3 10
где Кг = 20, 496 – коэффициент годичной аберрации

55.

56.

Явления, приводящие к
смещению сферических систем координат
Схема, поясняющая появление
прецессионного
движения земной оси:
- F , F1 , F2 силы, действующие на разные
участки объема Земли со стороны светила
L.
Причины прецессии земной оси

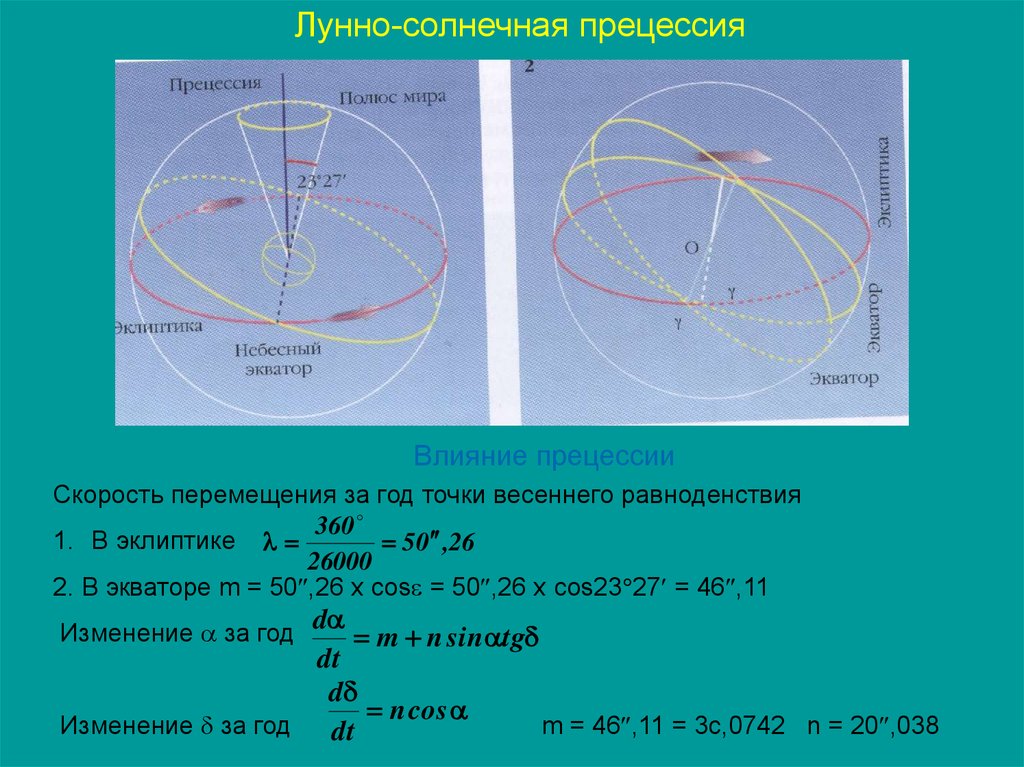
57.

Лунно-солнечная прецессия
Влияние прецессии
Скорость перемещения за год точки весеннего равноденствия
360
1. В эклиптике
50 ,26
26000
2. В экваторе m = 50 ,26 х cos = 50 ,26 х cos23 27 = 46 ,11
d
m n sin tg
dt
d
n cos
Изменение за год
m = 46 ,11 = 3c,0742 n = 20 ,038
dt
Изменение за год

58.

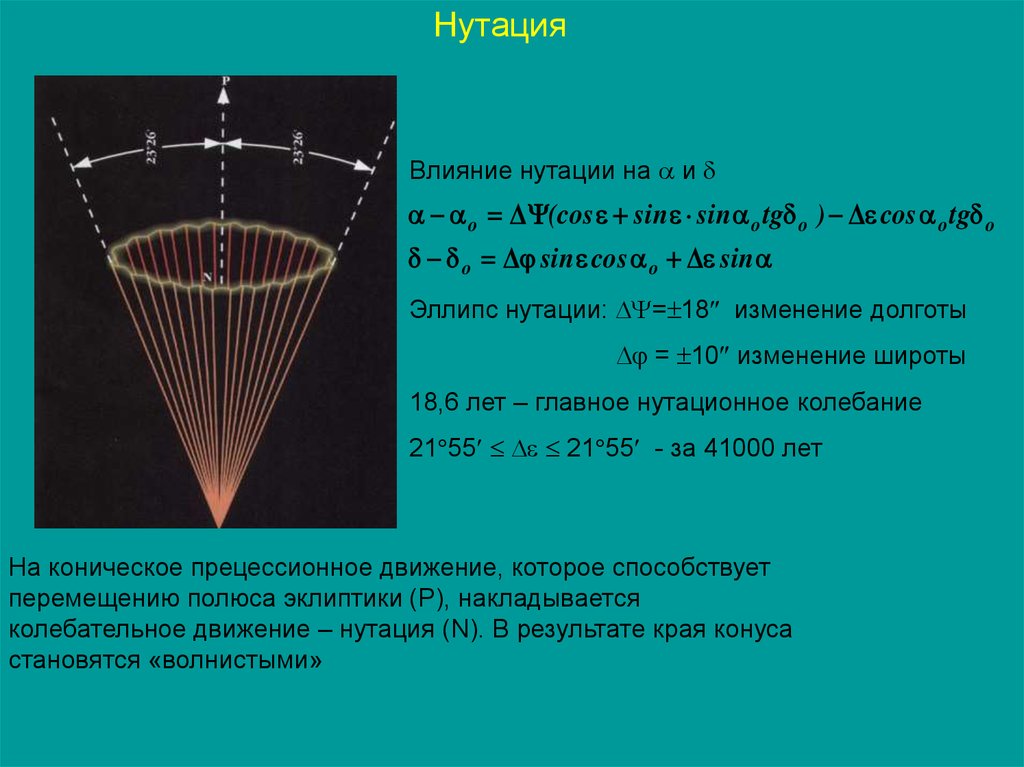
Нутация
Влияние нутации на и
o (cos sin sin o tg o ) cos o tg o
o sin cos o sin
Эллипс нутации: = 18 изменение долготы
= 10 изменение широты
18,6 лет – главное нутационное колебание
21 55 21 55 - за 41000 лет
На коническое прецессионное движение, которое способствует
перемещению полюса эклиптики (Р), накладывается
колебательное движение – нутация (N). В результате края конуса
становятся «волнистыми»

59.

Собственное движение звезд
Собственное движение звезды S0:
- собственное движение по
склонению;
- собственное движение по
прямому восхождению.
PN – северный полюс мира.
2 15 cos 2
cos
15 cos sin
Тангенциальная скорость
км
v 4 ,74
с
Полная скорость звезды в пространстве
Vr – лучевая скорость
v v 2 v r2

60.

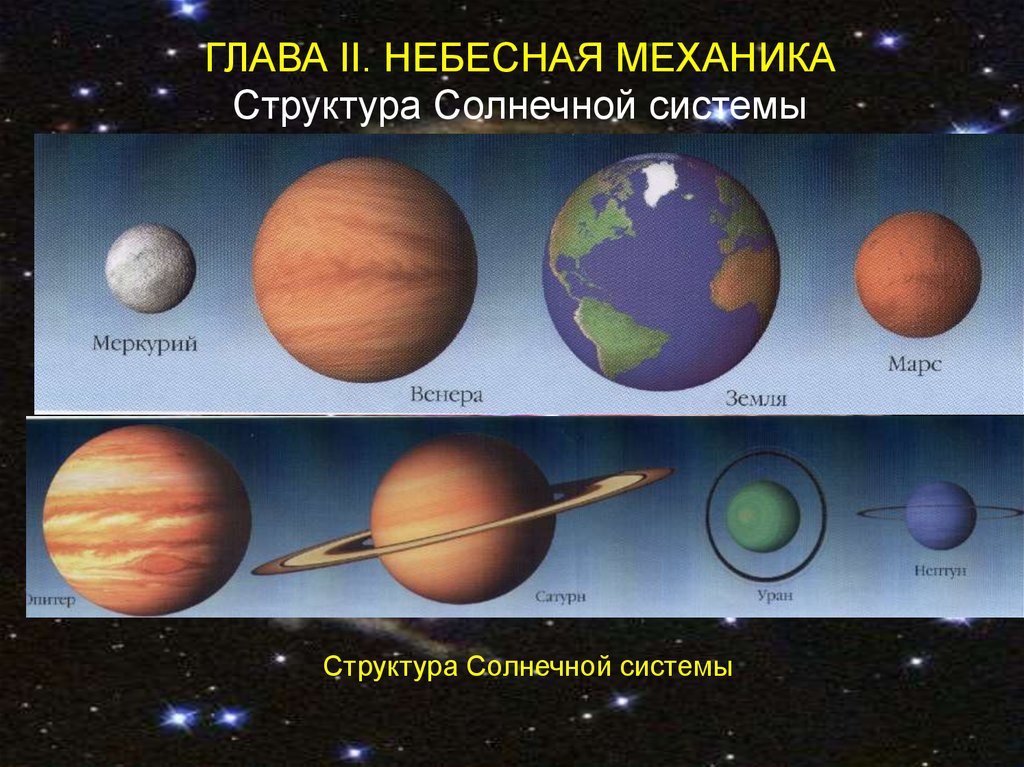
ГЛАВА II. НЕБЕСНАЯ МЕХАНИКА
Структура Солнечной системы
Структура Солнечной системы

61.

Пространственные системы координат
P
T
P
Геоцентрические (центр Т Земля) сферические
эклиптические координаты и
0 360
-90 +90

62.

Пространственные системы координат
P
S
0
T
P
1
0
Гелиоцентрические (центр S Солнце) сферические эклиптические системы
координат тела Р и и их связь с геоцентрическими координатами и
0 360
-90 +90

63. Условия видимости небесных тел. Конфигурации. Синодический период

S – синодический период
Т - сидерический период Земли
Т – сидерический период планеты
360 n 360
n
T
T
S
L n S
V
V
360
360
S и L nS
S
T
T
360
360
S 360
S
T
T
L
L0 = n S
К выводу формулы
продолжительности
синодического периода
В общем случае
1 1 1
S T T
Для нижних планет
1
1 1
S T T
Для верхних планет
1 1
1
S T1 T2
где Т1 – сидерический период планеты, находящейся ближе к Солнцу,
чем планеты с сидерическим периодом Т2 (Т2>Т1)

64.

Конфигурации нижних планет:
V1 – восточная элонгация;
V2 – нижнее соединение;
V3 – западная элонгация;
V4 – верхнее соединение
Конфигурации верхних планет:
М1 – восточная квадратура;
М2 – соединение;
М3 – западная квадратура;
М4 – противостояние.

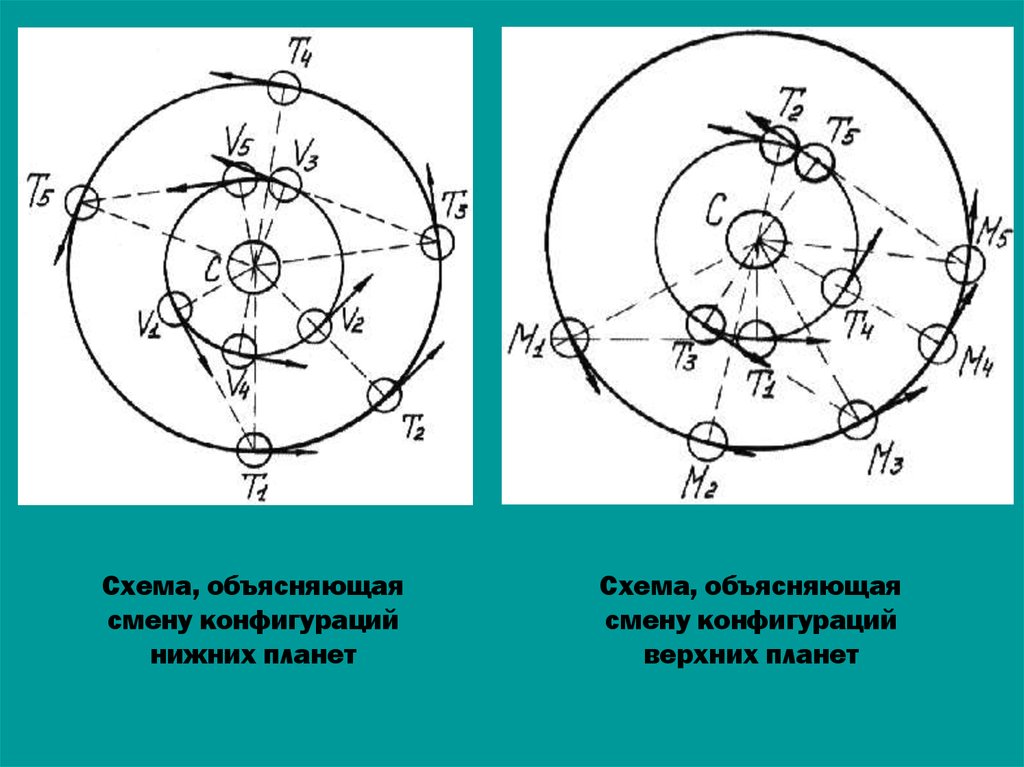
65.

Схема, объясняющая
смену конфигураций
нижних планет
Схема, объясняющая
смену конфигураций
верхних планет

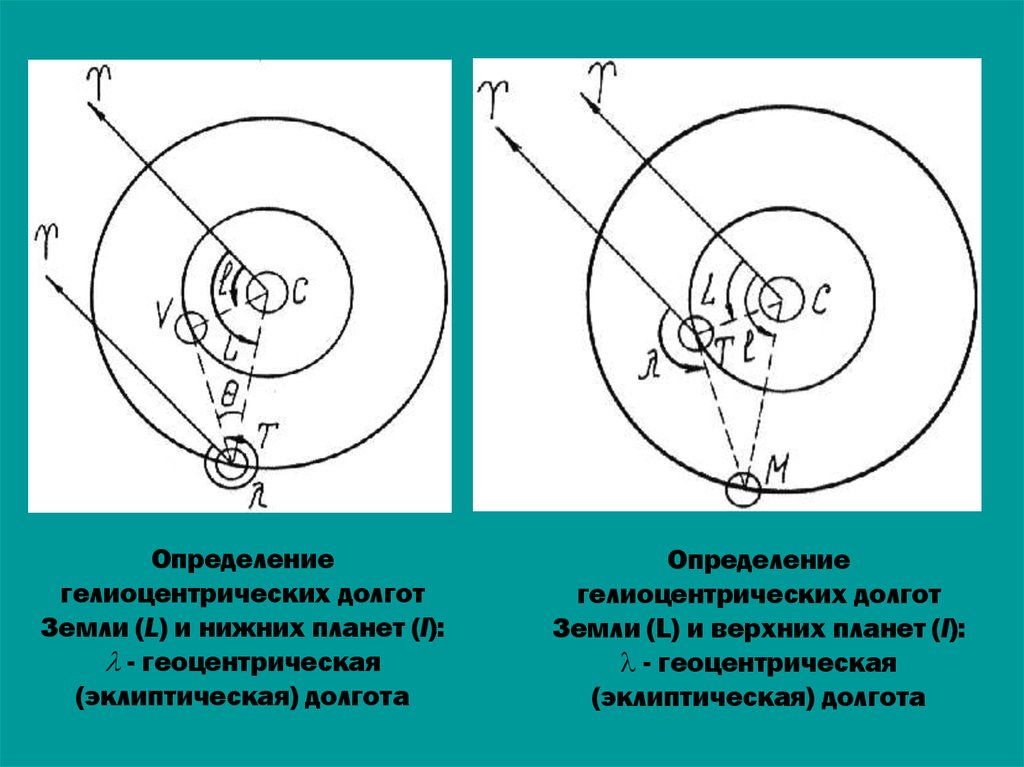
66.

Определение
гелиоцентрических долгот
Земли (L) и нижних планет (l):
- геоцентрическая
(эклиптическая) долгота
Определение
гелиоцентрических долгот
Земли (L) и верхних планет (l):
- геоцентрическая
(эклиптическая) долгота

67.

Соотношение между геоцентрическими Соотношение между
и гелиоцентрическими долготами дня геоцентрическими и
нижних планет:
гелиоцентрическими
долготами дня верхних планет:
а) нижнее соединение (V2)
o = ; o =
o – геоцентрическая долгота Солнца
o - гелиоцентрическая долгота Земли
б) верхнее соединение (V4)
o = ; 180 = - o
в) восточная элонгация (V1)
- о = ; - о = 270 +
г) западная элонгация (V3)
- о = - ; - о = 90 -
а) противостояние (М4)
- o = -180 ; - о = 0
б) соединение (М2)
- o = 0 ; - о = 180
в) восточная квадратура (М1)
- o = 0 ; - о = -
г) западная квадратура (М3)
- o = -90 ; - о =

68. Великие противостояния

rmin = q – ao = a(1-e) – ao,
rmax = Q – ao = a(1-e)– ao
е = 0,093; а = 1,524ао – для Марса
rmax
1,83
rmin
Если r 0,4 а.е. = 60 · 106 км – великие противостояния
Условие повторения великих противостояний
mT = nS,
где Т – сидерический период Марса, равный 687д=1,881Т , а S = 780д = 2,136Т
1,881 m = 2,136n
Отсюда 15,05 и 14,95 года; 16,93 и 17,09 года.
Последнее противостояние было в 2005 году.
Планета
n
Таблица. Среднее суточное движение планет
Меркурий Венера Земля
Марс Юпитер Сатурн
245 ,5
96 ,1
59 ,1
31 ,4
5
2

69.

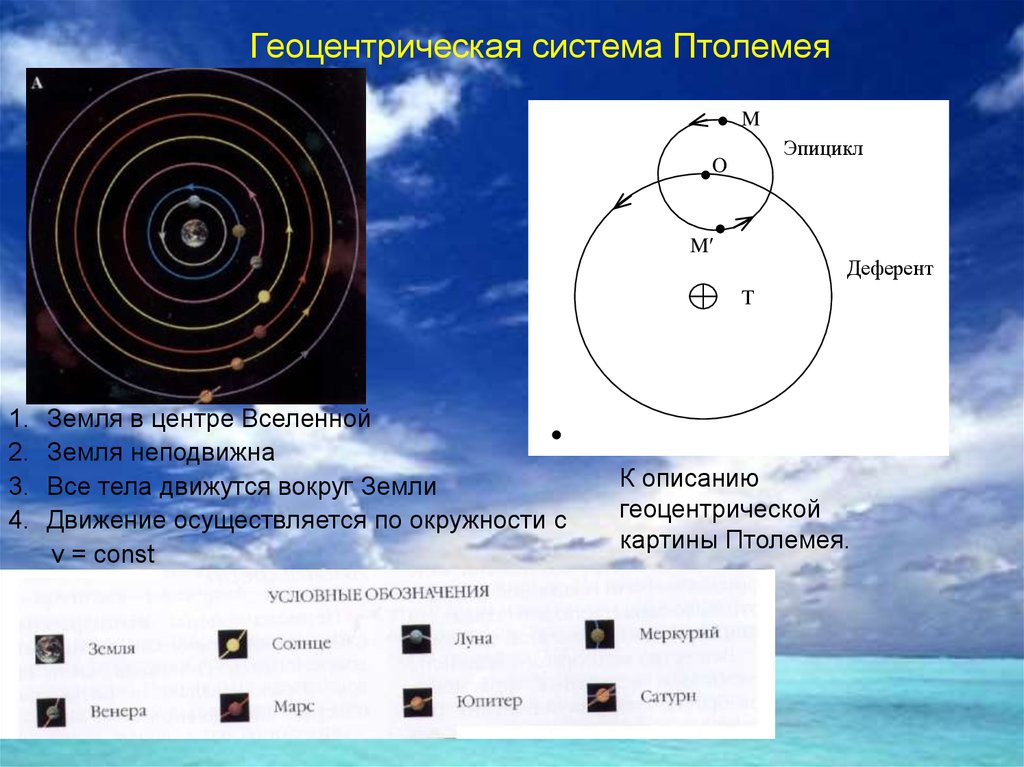
Геоцентрическая система Птолемея
M
Эпицикл
O
M
Деферент
T
1.
2.
3.
4.
Земля в центре Вселенной
Земля неподвижна
Все тела движутся вокруг Земли
Движение осуществляется по окружности с
v = const
К описанию
геоцентрической
картины Птолемея.

70. Система мира Коперника

1. В центре мира Солнце, а не Земля.
2. Шарообразная Земля вращается вокруг своей оси, и это вращение объясняет
кажущееся суточное движение всех светил.
3. Земля, как и все планеты, обращается вокруг Солнца, что и объясняет
видимое движение Солнца на фоне звезд.
4. Все движения – это комбинация равномерных круговых движений.
5. Кажущиеся прямые и попятные движения планет принадлежат не им, а Земле,
т.е. каким образом их видит движущийся вместе с Землей наблюдатель.

71.

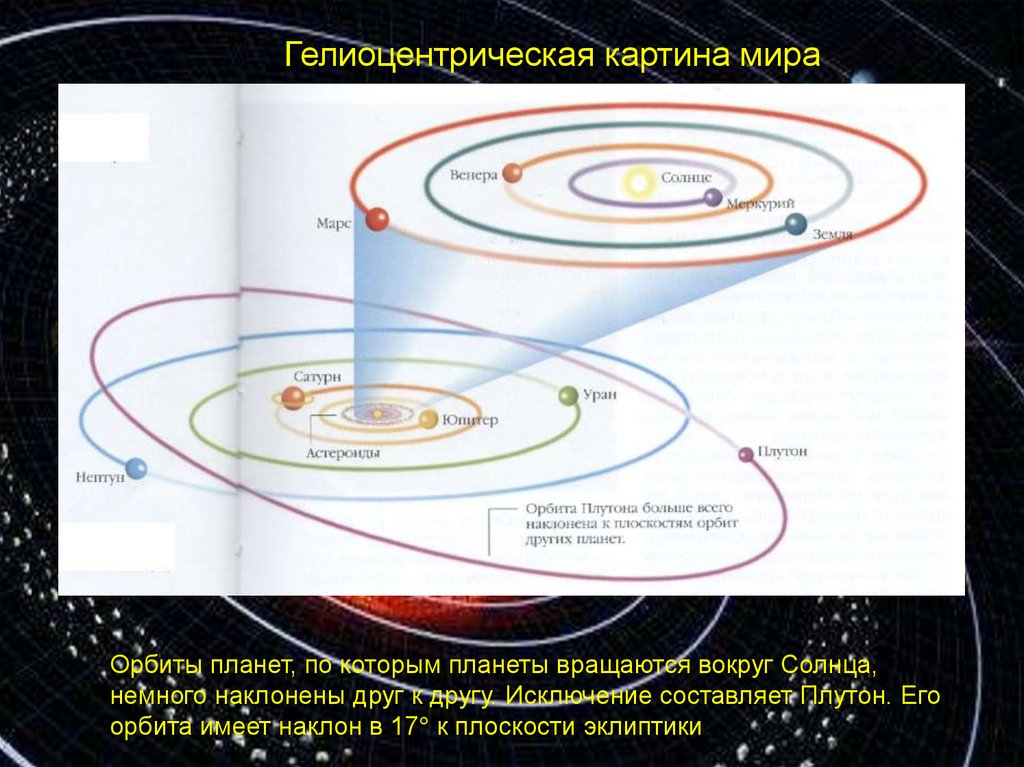
Гелиоцентрическая картина мира
Орбиты планет, по которым планеты вращаются вокруг Солнца,
немного наклонены друг к другу. Исключение составляет Плутон. Его
орбита имеет наклон в 17 к плоскости эклиптики

72.

1-й закон. Все планеты движутся по эллипсам,
в одном из фокусов которых (общем для
всех планет) находится Солнце.
2-й закон. Радиус-вектор планеты в равные
промежутки времени описывает
равновеликие площади.
3-й закон. Квадратуры сферических периодов
обращений вокруг Солнца
пропорциональны кубам больших полуосей
их эллиптических орбит
T12
2
T2
a 13
3
a2
T a3
(T =1, a = 1)

73.

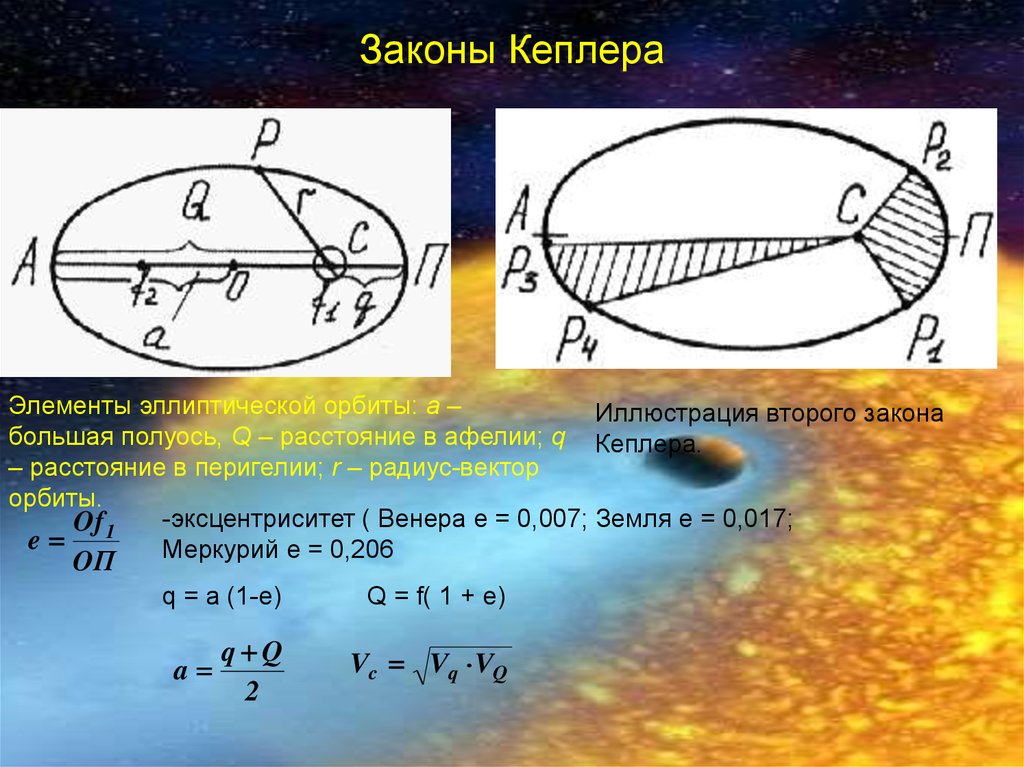
Законы Кеплера
Элементы эллиптической орбиты: a –
Иллюстрация второго закона
большая полуось, Q – расстояние в афелии; q Кеплера.
– расстояние в перигелии; r – радиус-вектор
орбиты.
-эксцентриситет ( Венера е = 0,007; Земля е = 0,017;
Of 1
e
Меркурий е = 0,206
OП
q = a (1-e)
Q = f( 1 + e)
q Q
2
Vc Vq VQ
a

74. Движение тел в поле тяготения Законы Ньютона

Первый закон: «Всякое тело продолжает удерживаться в своем
состоянии покоя или равномерного и прямолинейного движения
пока и поскольку оно не принуждается приложенными силами
изменить это состояние».
mv const
Второй закон: «Скорость изменения количества движения
пропорциональна
приложенной
силе
и
происходит
по
направлению» той прямой, по которой эта сила действует
d
( mv ) F
dt
Третий
закон:
«Действие
всегда
вызывает
равное
и
противоположное противодействие, т.е. взаимодействие двух тел
между собой равны и направлены в противоположные стороны».
d
d
( m1v1 ) ( m 2 v
dt
dt
F1 F2

75. Закон всемирного тяготения

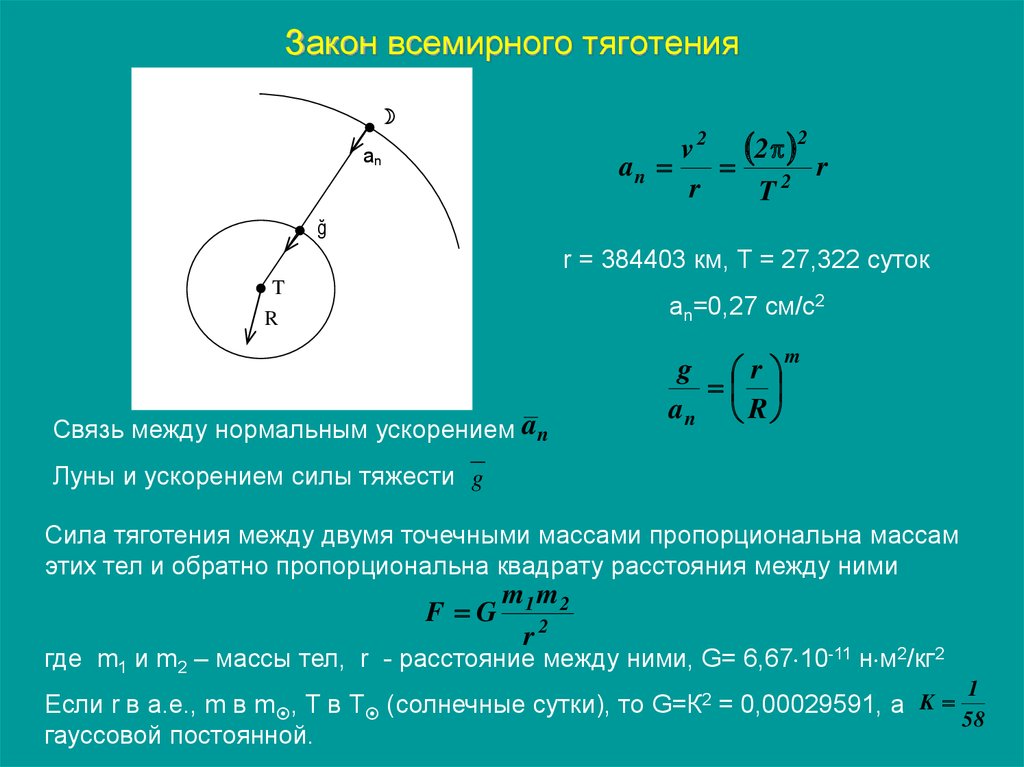
v 2 2 2
an
r
2
r
T
an
ğ
r = 384403 км, Т = 27,322 суток
T
R
an=0,27 см/с2
Связь между нормальным ускорением a n
g r
an R
m
Луны и ускорением силы тяжести g
Сила тяготения между двумя точечными массами пропорциональна массам
этих тел и обратно пропорциональна квадрату расстояния между ними
F G
m1 m 2
r2
где m1 и m2 – массы тел, r - расстояние между ними, G= 6,67 10-11 н м2/кг2
1
Если r в а.е., m в m , Т в Т (солнечные сутки), то G=К2 = 0,00029591, а K
58
гауссовой постоянной.

76. Гравитационная сила - пример центральной силы

Силы, где F c
2
F
U
c
2
r r
- центральные
r
U( r )
c
const
r
r
ro
r
GM 1 M 2 c
U( r )
r
r
c
F 2 ro
r
с = - GM1M2
Закон всемирного тяготения справедлив для
1. Тел, имеющих форму шаров с равномерно распределенной плотностью
вещества.
2. Тел, имеющих форму шаров со сферически симметричным распределением
плотности, зависящей от расстояния от центра шара.
В этих случаях сила взаимодействия между точечной массой М1 и шаром
массы М и радиусом Ro<r выразится формулой
GM 1 M
F
r2
где r – расстояние между точечной массой и центром шара.
Потенциальная энергия пробной массы в поле тяготения сплошного шара
равна U GM 1 M
r
3. Шаровых слоев, у которых вещество имеет постоянную плотность.
В случае взаимодействия точечных масс М1 с массами в виде шарового слом
GM 1 M ш
Мm выразится формулами
GM 1 M ш и
U
F
r
r2
для силы и потенциальной энергии, соответственно

77. Задача двух тел

F m
M1
N
r
r1
M2
r0
Rу.м.
r2
Движение двух тел под
действием центральных сил
Rц .м .
Закон сохранения
d r
d r
количества
M 1 21 M 2 22 const движения
dt
dt
замкнутой системы
M 1 r1 M 2 r2
dR
const
M1 M2
dt
d 2 ( r1 r2 )
dt 2
1
1
1
M1 M2
dt 2
GM 1 M 2
d 2 r2 GM 1 M 2
d 2r
M1
ro ; M 2
ro
2
2
dt
dt
r
r
r
r
o
r r1 r2
|r |
2
O
d 2r
2
, т.е. центр масс движется с постоянной
скоростью.
1
d 2r
1 GM 1 M 2
ro
2
dt
M1 M2 r
- приведенная масса
GM 1 M 2
d 2r
ro
2
dt
r

78.

dr
L r
const
dt
т.е. момент количества движения материальной точки ( ) L , движущейся
Для приведенной массы справедливо выражение
вокруг неподвижного центра сил (центра масс) есть величина постоянная.
L r и
dr
v
dt
, т.е. движение в одной плоскости
Преобразуем уравнение движения к виду
M M
v 2
G 1 2 E
2
r
y
Сумма кинетической энергии тела массой и его
потенциальной энергии – постоянна.
v
V
V 0
0
ro
O
dr dr
d
dr
ro r
o ro r o
dt dt
dt
dt
L r 2 ro o ( r ro )
Vr0
N
r
M1M2
d v 2
0
G
dt 2
r
L r 2 r 2
x
d
const
dt
Представление скорости движения
приведенной массы (т.N) вокруг
неподвижного центра сил в точке О

79.

d
r
rd
d
O
1
r rd const
2
За равные промежутки времени
радиус-вектор точки описывает
равные площади (второй закон
Кеплера)
d
К определению секторальной
скорости
В полярной системе координат
2
2
2
2
1 dr
d
1
dr
L
E r 2 U ( r )
U( r )
2
2 dt
dt
2
dt
2 r
U эфф
L2 - определяет одномерное движение в поле
U( r )
2 r 2 «эффективной» потенциальной энергии
L2
2 r 2
- центробежная энергия, связанная со вращающейся вокруг N
неподвижной системы координат
Е=Uэфф, если
dr
0
dt
движущегося тела
- условие границы области пространства

80.

Если 1) r rmin – движение инфинитное
2) rmin r rmax – движение финитное, лежащее внутри кольца,
ограниченного окружностями r = rmin и r = rmax
Если 1) E > Uэфф – движение инфинитное
Е < Uэфф – движение финитное
Траектория движения определится интегрированием по t выражения для Е
L
r
2
d2
2 E U ( r )
L2
r2
Зависимость от времени (время прохождения точки траектории с заданными
и r) определится интегрированием по r
t
Ldt
r 2
L
r
2
d2
2 E U ( r )
L2
r2

81. Кеплерова задача

c
U ( r ) , где с=М1М2G
r
Пусть
L2
p
GM 1 M 2
e 1
P
O
r max
- эксцентриситет
уравнение конического сечения
x
2b
GM 1 M 2 2
p
1 e cos
Тогда r
y
a e
L
GM 1 M 2
r
arccos
GM 1 M 2 2
2 E
2
L
2 EL2
r min
2a
1) Если Е < 0, то е < 1
движение финитное (эллипс или
окружность)
GM 1 M 2
a
2
2E
1 e
p
b
Основные элементы эллипса: а –
большая полуось; в – малая полуось;
р - параметр; е - эксцентриситет
rmin
p
1 e2
L
2 E
-большая
полуось
- малая
полуось
p
p
a (1 e); rmax
a (1 e)
1 e
1 e

82.

d
Т.к. l r
, то LT = 2 ( = ab)
dt
- Квадраты периодов обращения по эллиптическим
T 2 ( M 1 M 2 ) 4 2
3
G орбитам, пропорциональным кубу их линейных
a
размеров
2
2) Если Е > 0, то е > 1 – движение инфинитное по гиперболе, огибающей
фокус 0
p
p
rmin
1 e
2
3) Если Е = 0, то е = 1 – движение инфинитное по параболе, огибающей
фокус 0
Из выражения для энергии,
заменив Е, получим
2 1
v 2 G ( M 1 M 2 )
r a
1. е= 0 rmax = rmin = a
1
v G( M 1 M 2 )
a
2. е = 1
v 2 G( M 1 M 2 )
1
r

83.

Из выражения для энергии, заменив Е, получим
1. е= 0 rmax = rmin = a
r = rmin
v G( M 1 M 2 )
v 2 G( M 1 M 2 )
1
1
a
2 1
v G ( M 1 M 2 )
r a
2
(круговая орбита)
r = rmax v = 0 a =
rmin
y
P1
P
x
O
r min
Параметры орбиты инфинитного
движения
P2
Различные типы орбит
приведенной массы

84. Законы Кеплера в рамках задачи двух тел

1. Первый (обобщенный) закон Кеплера.
Под действием сил тяготения одно тело движется в поле тяготения другого
по орбите, форма которой представляет собой один из видов
количественного сечения – окружность, эллипс, парабола или гипербола.
При этом форма и размер орбит тел зависит только от начальной скорости.
2. Второй закон Кеплера.
При невозмущенном движении (в задаче двух тел)
радиус-вектор тела за равные промежутки
времени описывает равновеликие площади.
y
rd
d
O
d
r
const
dt
r
2
x
К объяснению второго
закона Кеплера
- истинная аномалия (Для Солнца, как центра
притяжения, - угол между направлениями из
центра Солнца на планету и на перигелий ее
орбиты)
3. Третий (уточненный) закон Кеплера.
Квадраты периодов обращения планет вокруг Солнца относятся как кубы
больших полуосей эллипсов.
T2 M m
a3
1
T22
1
1
M 2 m2
1
a 23

85. Характеристики эллиптической орбиты небесного тела относительно Солнца

AN = a – большая полуось;
P
Q
A
O
a
П
c
N O
Характеристики
эллиптической орбиты
q
NC
e
NП
- эксцентриситет;
А – афелий; П – перигелий
q = CП = a(1-e)
Q = AС = a(1+e)
N –центр эллипса;, О (С), О фокусы
r – радиус-вектор планеты Р.
v q v кр
v Q v кр
1 e
1 ve
1 e
1 e

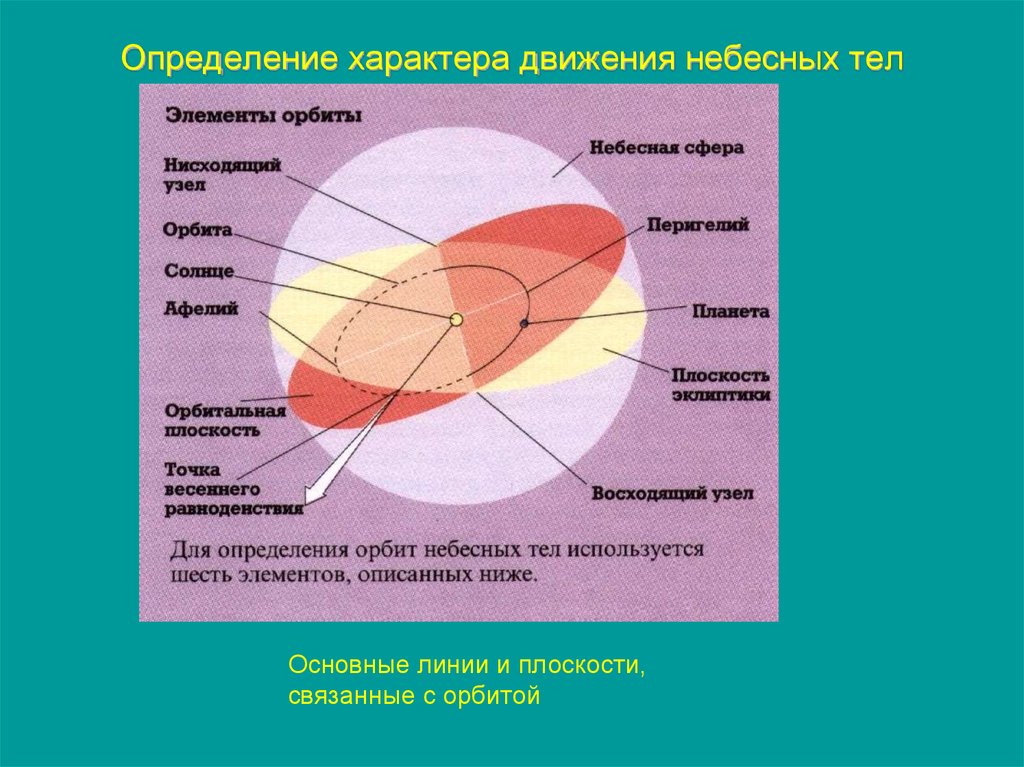
86. Определение характера движения небесных тел

Основные линии и плоскости,
связанные с орбитой

87.

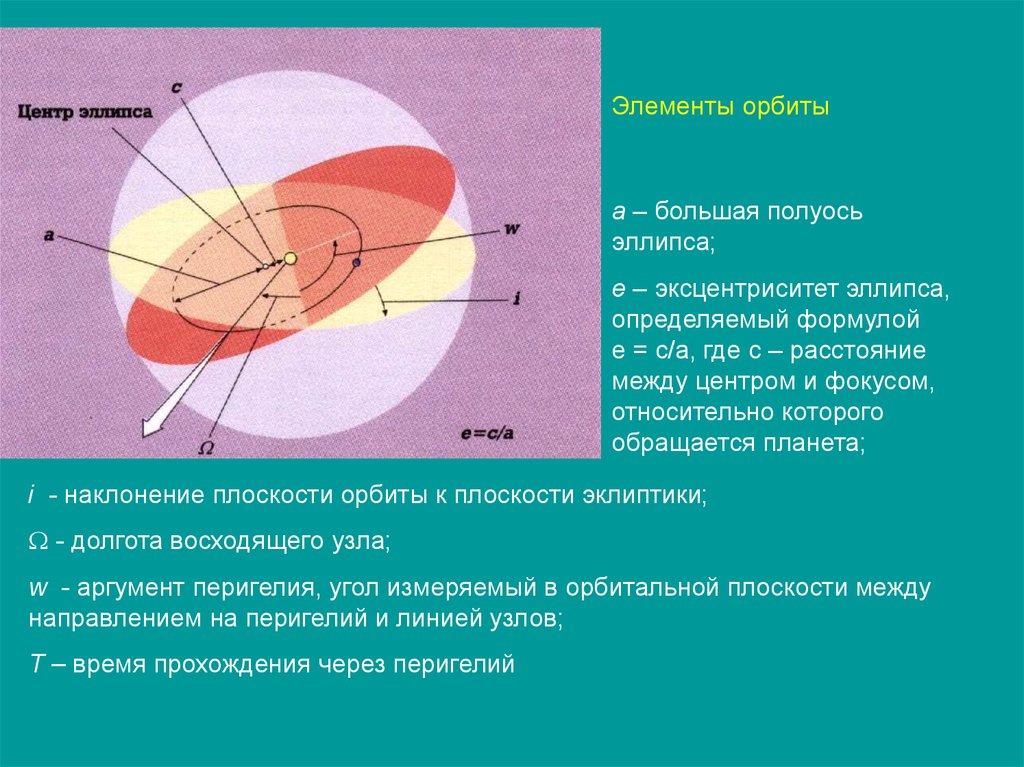
Элементы орбиты
а – большая полуось
эллипса;
е – эксцентриситет эллипса,
определяемый формулой
е = с/а, где с – расстояние
между центром и фокусом,
относительно которого
обращается планета;
i - наклонение плоскости орбиты к плоскости эклиптики;
- долгота восходящего узла;
w - аргумент перигелия, угол измеряемый в орбитальной плоскости между
направлением на перигелий и линией узлов;
Т – время прохождения через перигелий

88.

Определение и r для
оценки положения
небесного тела на орбите
в момент времени t
1. r = a(1 – e·cosE) –
уравнение Кеплера
tg
Q
2
1 e E
tg
1 e 2
2. М = Е - e·sinE – средняя
аномалия
3.
Истинная ( ) и эксцентрическая (Е)
аномалии орбиты.
4.
tg
2
1 e E
tg
1 e 2
2
t T
M
T
T - сидерический период

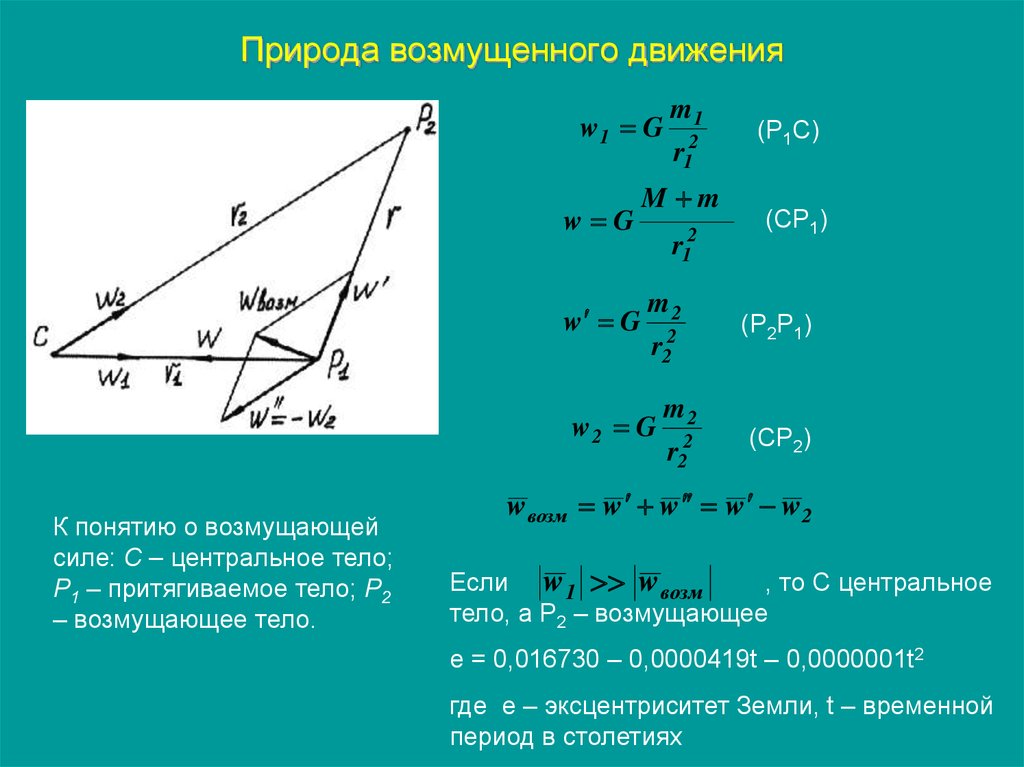
89. Природа возмущенного движения

w1 G
w G
w G
r12
M m
r12
m2
r22
w2 G
К понятию о возмущающей
силе: С – центральное тело;
Р1 – притягиваемое тело; Р2
– возмущающее тело.
m1
m2
r22
(Р1С)
(СР1)
(Р2Р1)
(СР2)
wвозм w w w w 2
Если w 1 w возм
, то С центральное
тело, а Р2 – возмущающее
е = 0,016730 – 0,0000419t – 0,0000001t2
где е – эксцентриситет Земли, t – временной
период в столетиях

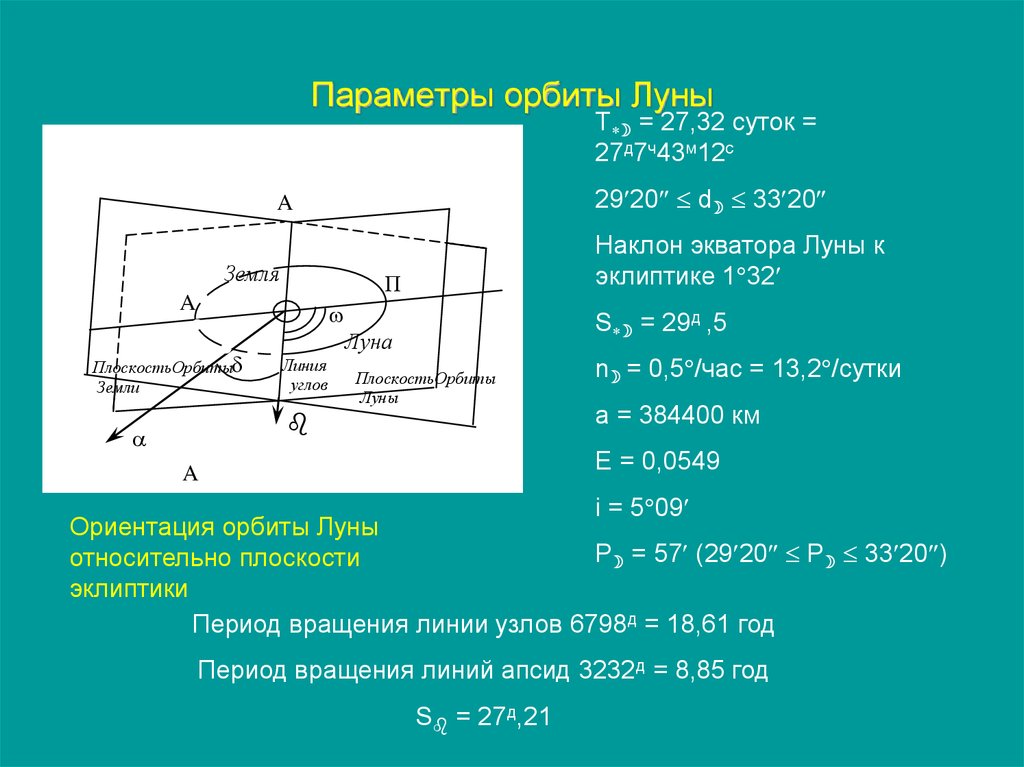
90. Параметры орбиты Луны

Т = 27,32 суток =
27д7ч43м12с
29 20 d 33 20
A
Земля
Наклон экватора Луны к
эклиптике 1 32
П
A
ПлоскостьОрбиты
Земли
S = 29д ,5
Луна
Линия
углов
ПлоскостьОрбиты
Луны
n = 0,5 /час = 13,2 /сутки
а = 384400 км
Е = 0,0549
A
i = 5 09
Ориентация орбиты Луны
P = 57 (29 20 P 33 20 )
относительно плоскости
эклиптики
Период вращения линии узлов 6798д = 18,61 год
Период вращения линий апсид 3232д = 8,85 год
S = 27д,21

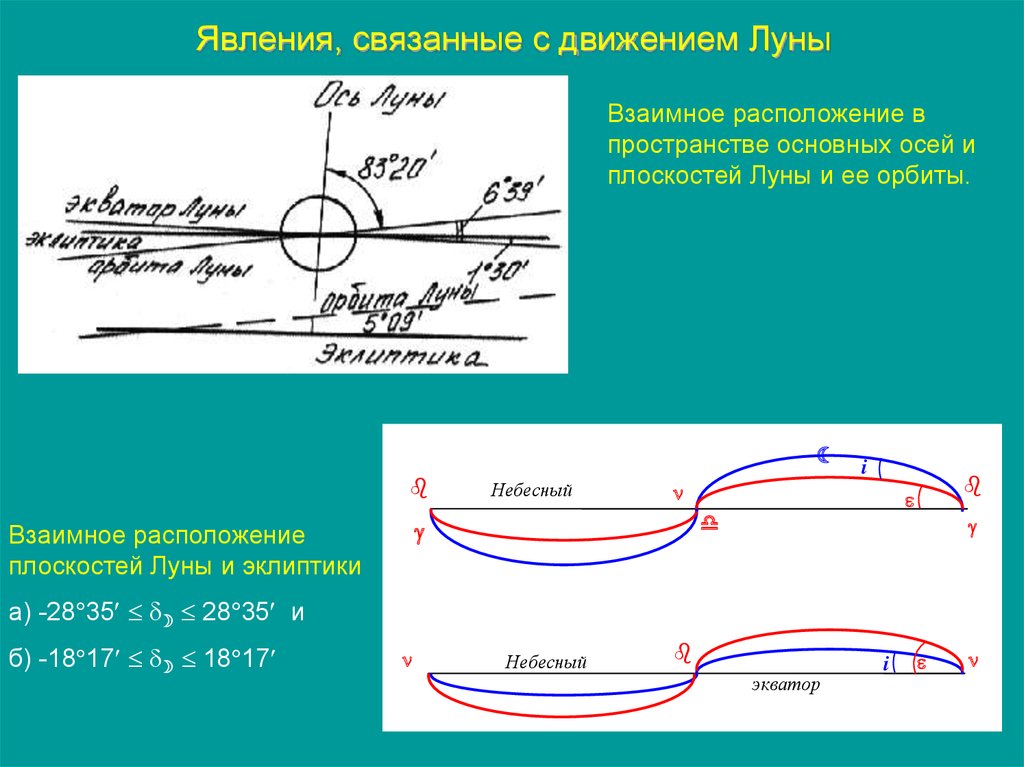
91. Явления, связанные с движением Луны

Взаимное расположение в
пространстве основных осей и
плоскостей Луны и ее орбиты.
Небесный
Взаимное расположение
плоскостей Луны и эклиптики
i
а) -28 35 28 35 и
б) -18 17 18 17
Небесный
экватор
i

92.

Либрация Луны
Либрация Луны по долготе
Либрация Луны по широте

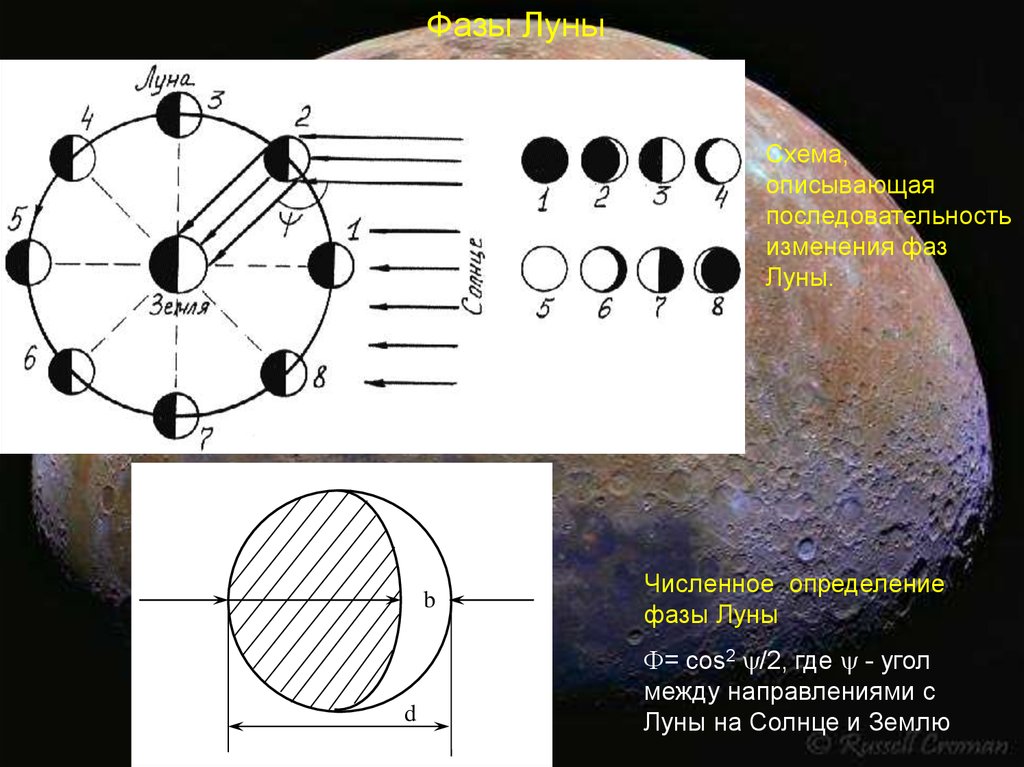
93.

Фазы Луны
Схема,
описывающая
последовательность
изменения фаз
Луны.
b
d
Численное определение
фазы Луны
= cos2 /2, где - угол
между направлениями с
Луны на Солнце и Землю

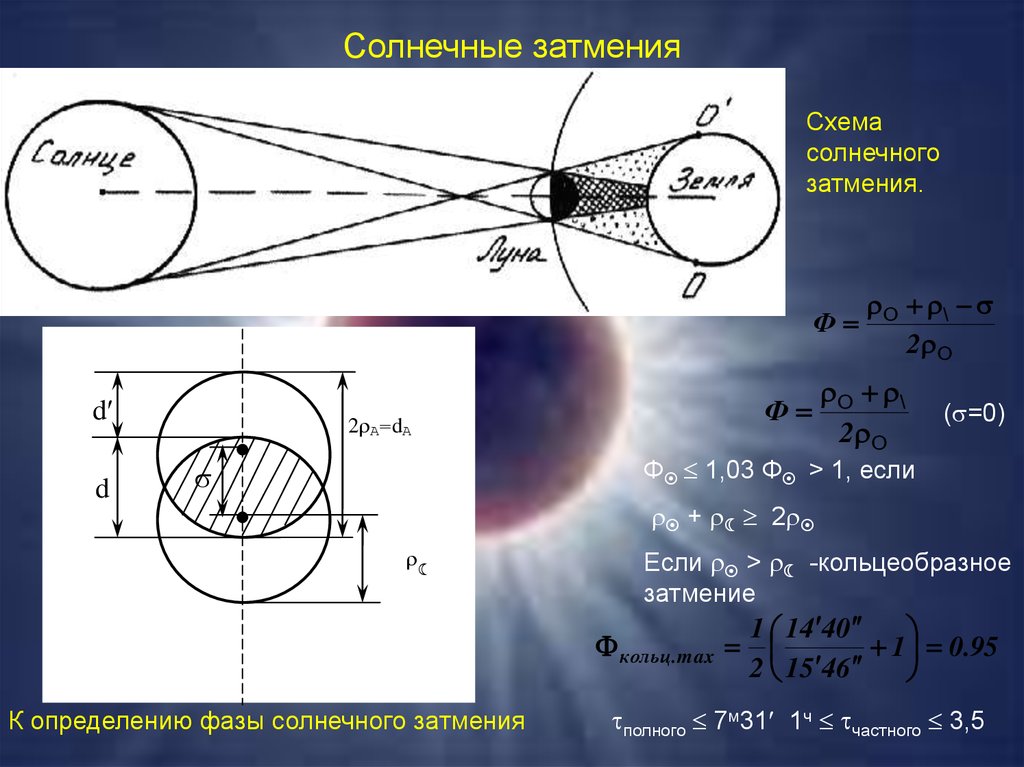
94.

Солнечные затмения
Схема
солнечного
затмения.
Ф
d
d
Ф
2 A=dA
\
2
\
2
( =0)
Ф 1,03 Ф > 1, если
+ 2
Если > -кольцеобразное
затмение
кольц.max
К определению фазы солнечного затмения
1 14 40
1 0.95
2 15 46
полного 7м31 1ч частного 3,5

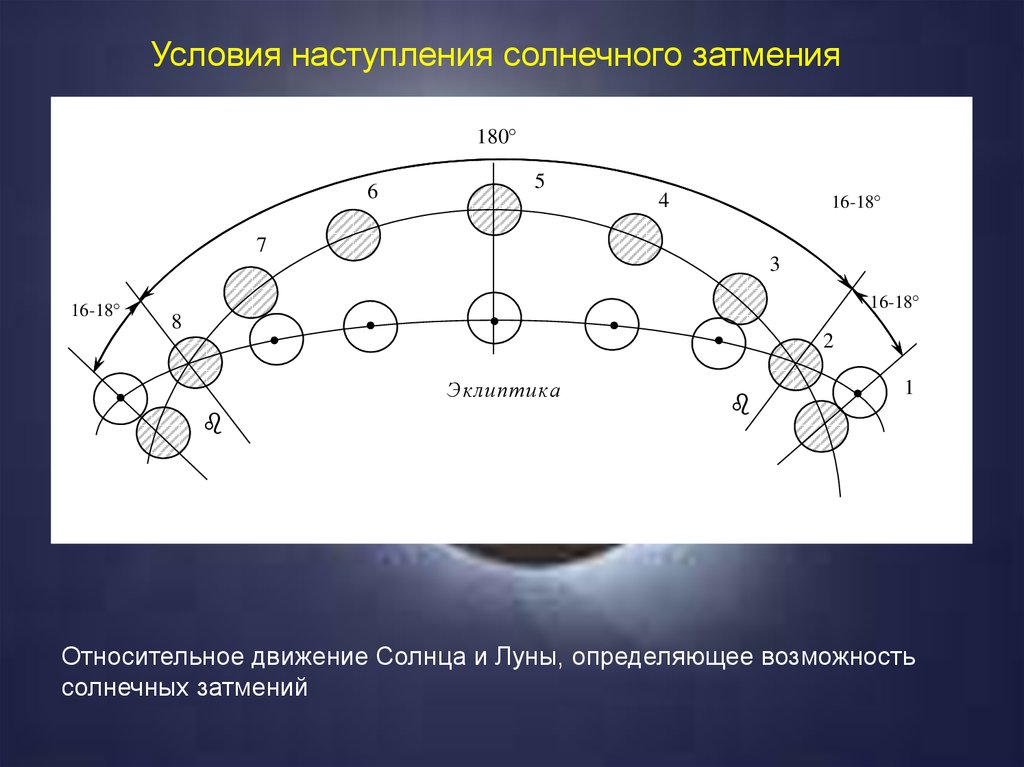
95.

Условия наступления солнечного затмения
180
6
5
4
16-18
7
16-18
3
16-18
8
2
Эклиптика
1
Относительное движение Солнца и Луны, определяющее возможность
солнечных затмений

96.

К расчету момента начала
солнечного затмения: , ℂ угловые радиусы Солнца и
Луны; Р , Рℂ - суточные
параллаксы Солнца и Луны.
= + + Р - Р
84 26 94 02
A
C
L
A
T
Определение условий
полного солнечного затмения
= - + Р - Р
55 06 60 36

97.

sin l= tg ctgi
l 11 12 - полные
солнечные затмения
l 18 19 - частные
солнечные затмения
l – эклиптическая долгота
- эклиптическая широта
i = 5 9
Сферический треугольник L в
момент начала солнечного затмения:
L - отрезок орбиты Луны, отрезок эклиптики.

98.

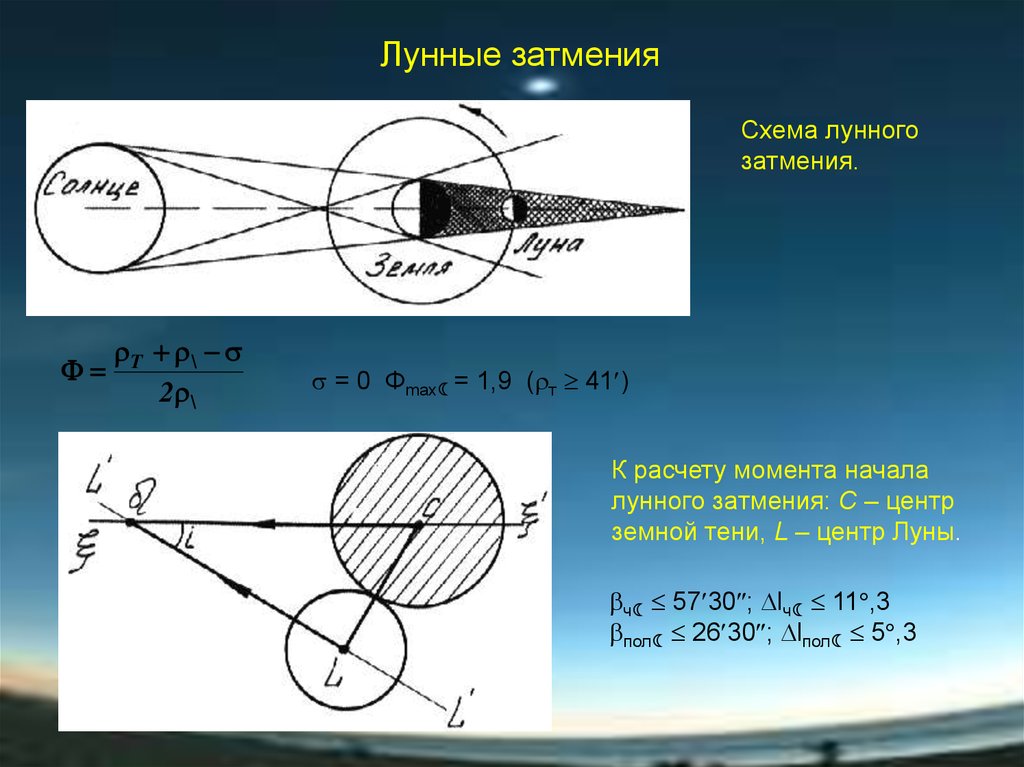
Лунные затмения
Схема лунного
затмения.
T \
2 \
= 0 Фmax = 1,9 ( т 41 )
К расчету момента начала
лунного затмения: С – центр
земной тени, L – центр Луны.
ч 57 30 ; lч 11 ,3
пол 26 30 ; lпол 5 ,3

99.

Частота повторения затмений. Сарос
Т = 365Д, 3 – 19д,3 = 346д – драконический год
S = 29д,53
223 S = 242 S = 19Т = 18л 11,3 суток – Сарос
S = 27д,21
За 18 л 11,3 суток: 70 71 затмение, из них 42 43 солнечных (14
полных и 13 14 кольцеобразных + 15 частных ) и 28 лунных

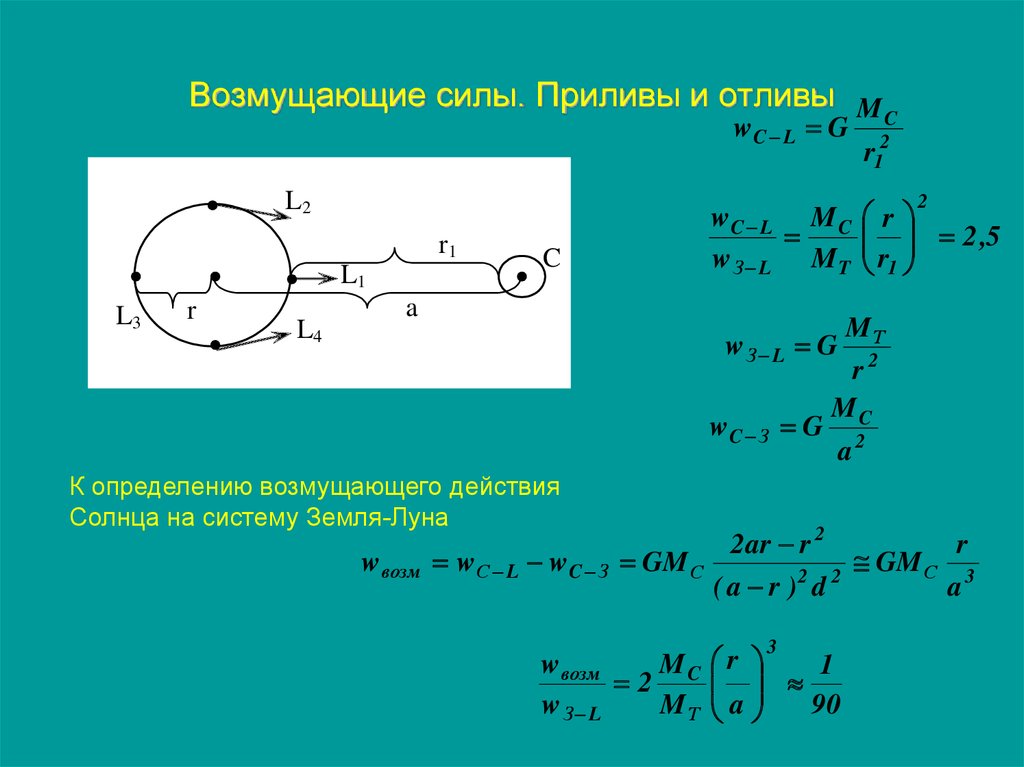
100. Возмущающие силы. Приливы и отливы

M
C
wC L G
L2
2
r1
L1
L3
r
L4
r12
C
wC L M C r
2 ,5
w З L M T r1
a
MТ
w З L G
wC З G
К определению возмущающего действия
Солнца на систему Земля-Луна
w возм w С L w C З
w возм
w З L
r2
MC
a2
2 ar r 2
r
GM С
GM
С 3
( a r )2 d 2
a
MC r
2
MТ a
3
1
90

101.

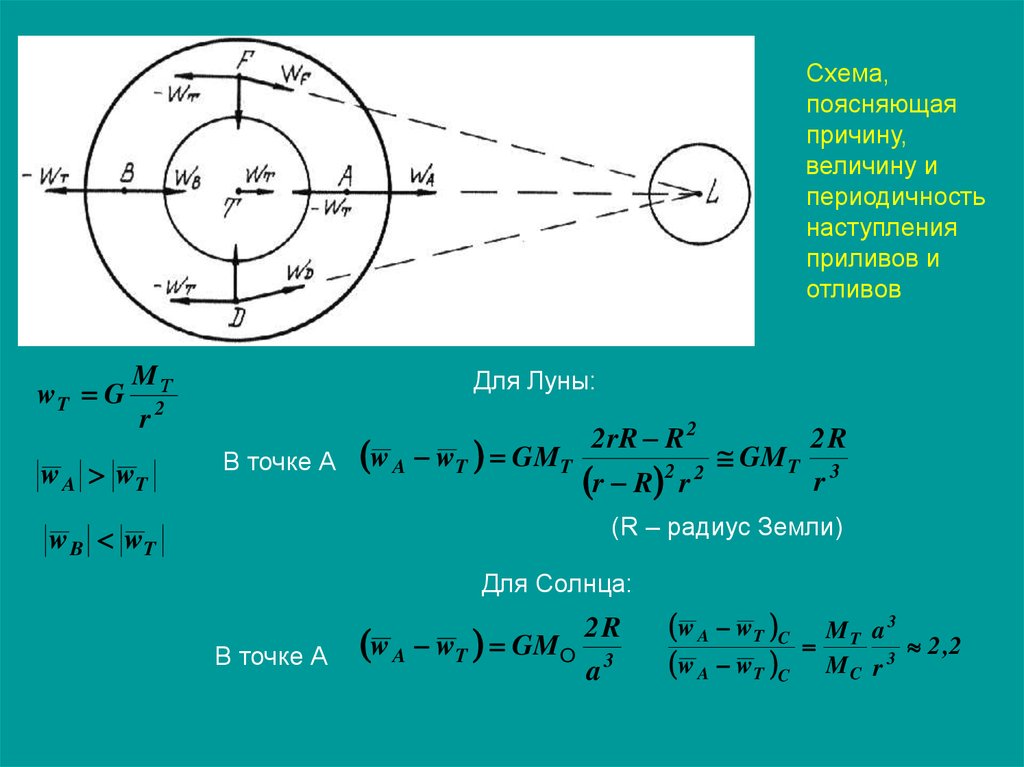
Схема,
поясняющая
причину,
величину и
периодичность
наступления
приливов и
отливов
wT G
MТ
Для Луны:
r2
w A wT
В точке А
w A wT GMT
2 rR R 2
r R 2 r 2
GMT
2R
r3
(R – радиус Земли)
w B wT
Для Солнца:
В точке А
w A wT GM 2 R3
a
w A wT C
w A wT C
MT a 3
2 ,2
3
MC r

102.

Движение космических аппаратов
«Вояджер-1» (оранжевая траектория) запущен 5 сентября 1977 гю, пролетел около
Юпитера 5 марта 1979 г., Сатурна – 12 ноября 1980 г., а затем резко повернул и
покинул солнечную систему. «Вояджер-2» (красная траектория) старт овал 20
августа 1977 г., раньше «Вояджера-1». Около Юпитера он пролетел 9 июля 1979 г.,
Сатурна – 25 августа 1981 г., Урана – 24 января 1986 г., Нептуна – 24 августа 1989
г. и также покинул Солнечную систему

103.

Искусственные спутники Земли
1. vo = v э < vc - эллипс (т.m –
апогей)
m
V0=
2. vo = vc – окружность
V э
Vr
Vс
3. vo = v э > vc - эллипс (т.m –
перигей)
M
V э
Vn
vo < 2vc
4. vo = 2vc - парабола
Типы орбит в зависимости от начальной
скорости vo (vo mM)
П
5. vo > 2vc - гипербола
2
e 1
hn
q
a
vq
Q ( 2Q q )
v
q( 2 q Q )
Q
q
2a
q = a(1-e) = RЗ +hП
Q = a(1+e) = RЗ +hA
Q
hА
А
Эллиптическая орбита ИСЗ

104.

VC G
M
ro
ro = RЗ + hП
Для эллиптической орбиты
при vo > vC
2
vo
ro
v o2
2 , e 2 1 , rA a 1 e
a
vc
vc
3
2 a 2
T M m
GM
Если ro R vc = 7,91 км/с
Т = 1,659 10-4 а3/2 мин
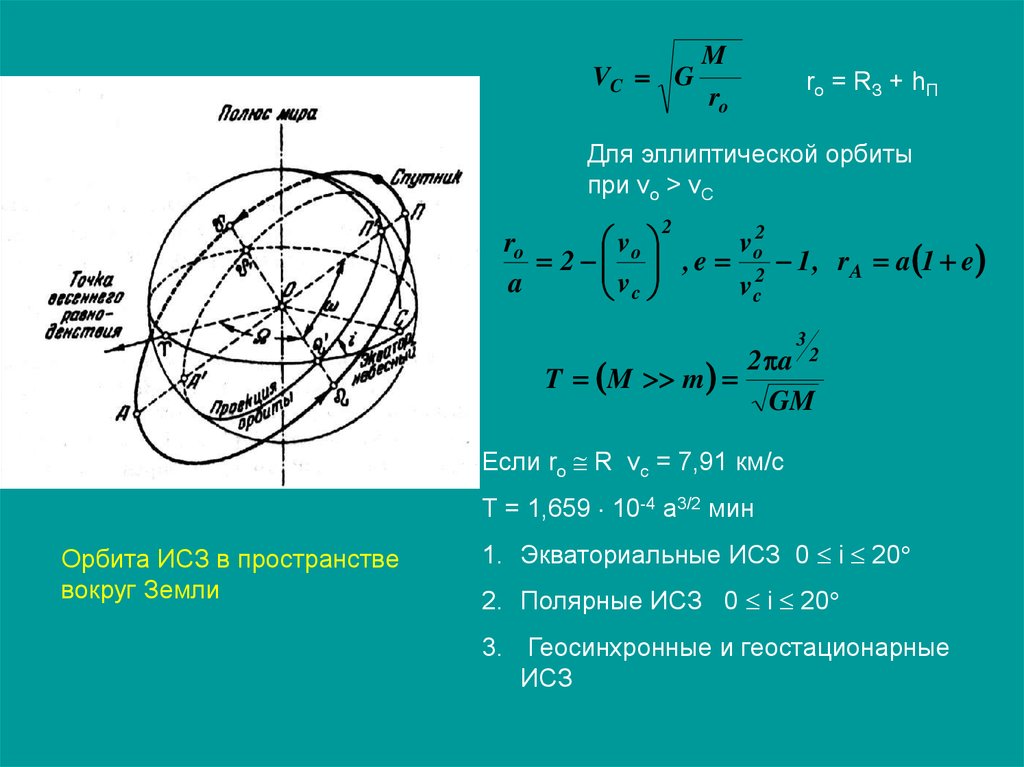
Орбита ИСЗ в пространстве
вокруг Земли
1. Экваториальные ИСЗ 0 i 20
2. Полярные ИСЗ 0 i 20
3. Геосинхронные и геостационарные
ИСЗ

105. Принципы движения КА

Если vo vп – движение КА по параболе или гиперболе
m
r
m
2
В системе Земля – Луна = 69000 км от Луны
К Солнцу
- радиус действия тела m относительно m ;
r – расстояние между ними
5
Орбита Луны
А
Земля
Орбита Земли
Изменение кинетической энергии КА
E E H E min
2
2
mv min
mv H
2
2
vH – начальная скорость относительно Земли,
vmin – скорость в точке на расстоянии
mM 3 U GmM 1 1
mM 3
U G
U H G
H
3
R
R3
1 1
2GM 3
v 2 v 2 2Gm 1 1 - Конечная
K
min
Л
скорость
R3
R Л сближения с Луной
Влияние Луны на
траекторию КА
2
2
v min
vH
1. Условия запуска КА к Луне
M3
m1
В точке
G 2 G
r 2

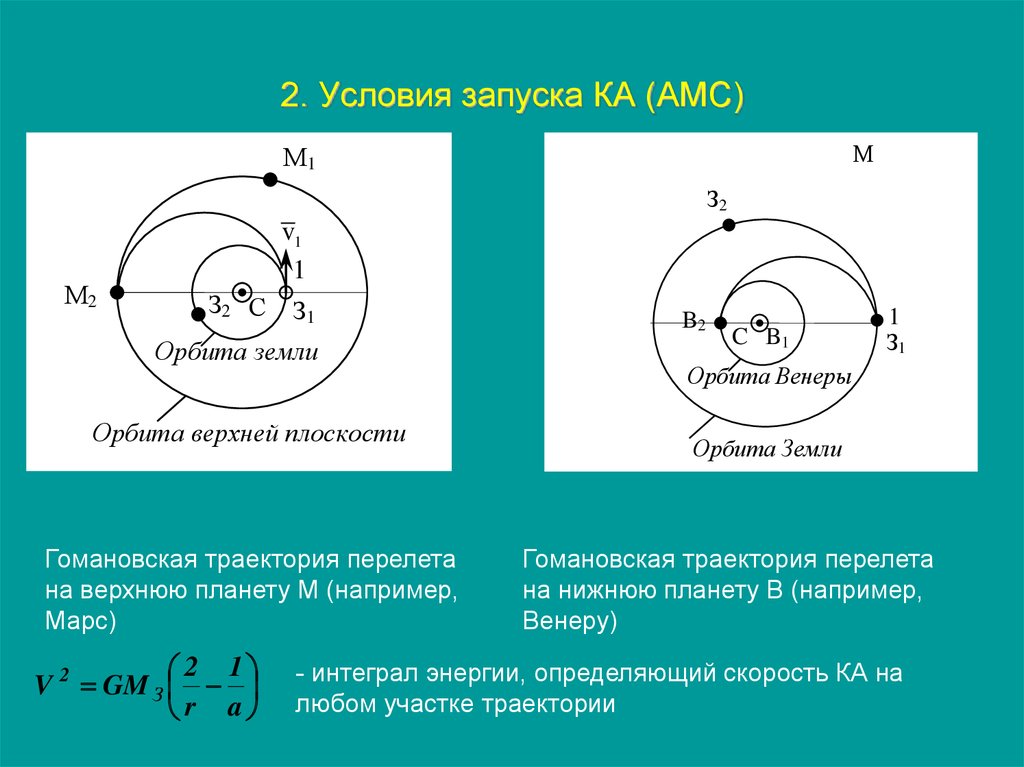
106. 2. Условия запуска КА (АМС)

М
М1
З2
М2
v1
1
З2 С З1
Орбита земли
Орбита верхней плоскости
Гомановская траектория перелета
на верхнюю планету М (например,
Марс)
2 1
V 2 GM З
r a
B2
C B1
1
З1
Орбита Венеры
Орбита Земли
Гомановская траектория перелета
на нижнюю планету В (например,
Венеру)
- интеграл энергии, определяющий скорость КА на
любом участке траектории

107.

Начальная скорость vo в случае запуска АМС относительно Земли за пределы
Солнечной системы орбиты vH определится так:
VH = Vq (относительно Солнца – парабола)
vдоп = VH - VЗ – дополнительная скорость аппарата с которой он покидает
сферу притяжения Земли
v доп = 42,3 км/с – 29,8 км/с = 12,5 км/с ; v доп = 42,3 км/с + 29,8 км/с = 72,1 км/с,
т.к.
VH
2GM
42 ,3 км / с
ao
(параболическая скорость относительно
Солнца)
vЗ = 29,8 – орбитальная скорость
v o2
v o2
2GM З Gm
RЗ h a
v доп 2
2GM
R h
2Gm
2
v пар
2
v доп
2GM З Gm
a
2
v o2 v n2 v доп
vo = 16,6 км/с; vo = 72,8 км/с
vo – III космическая скорость