Похожие презентации:
Теорема Виета
1. Теорема Виета
* ТеоремаВиета
2.
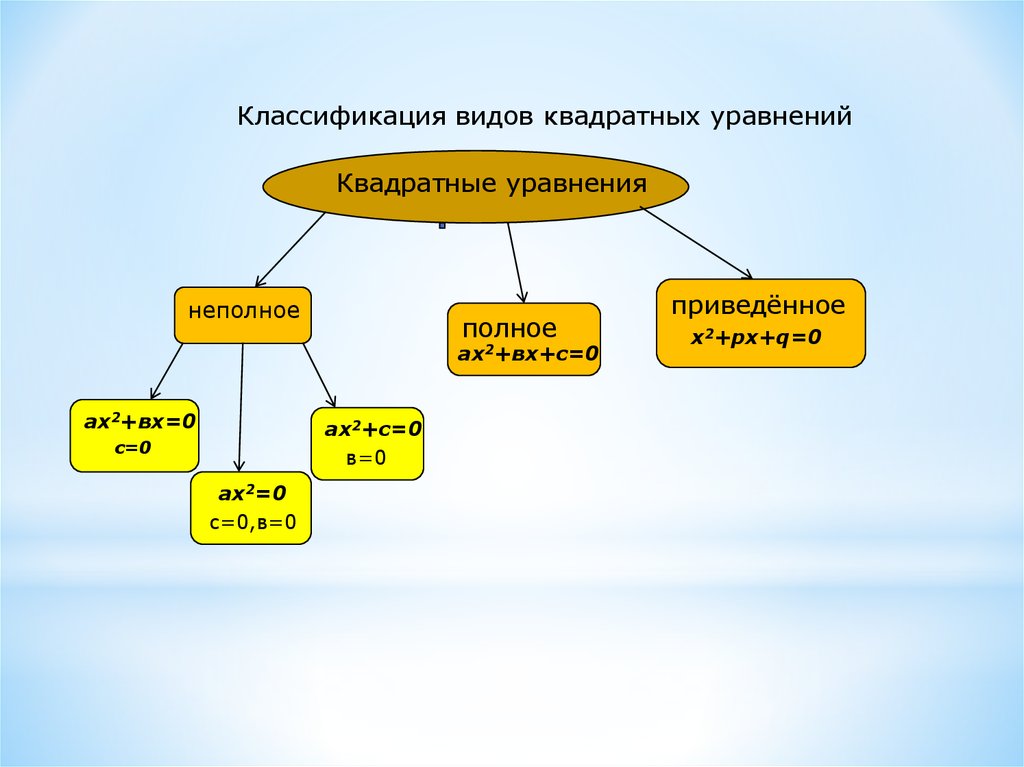
Классификация видов квадратных уравненийКвадратные уравнения
неполное
полное
ах2+вх+с=0
ах2+вх=0
ах2+с=0
в=0
с=0
ах2=0
с=0,в=0
приведённое
х2+pх+q=0
3. Обратим внимание
*Обратим внимание* Ещё одно интересное соотношение – дискриминант
уравнения равен квадрату разности его корней:
D=(x1-x2)2.
4. Теорема Виета
* Теорема ВиетаФрансуа Виет (1540–1603) родился во
Франции. Разработал почти всю
элементарную алгебру; ввёл в алгебру
буквенные обозначения и построил
первое буквенное исчисление.
5.
ТеоремаВиета
Искусство,
которое
я
излагаю,
ново…Все
математики знали, что под их алгеброй были
скрыты несравненные сокровища, но они не умели
их найти: задачи, которые они считали наиболее
трудными, совершенно легко решаются с помощью
нашего искусства.
Франсуа
Виет.
6.
Приведённое квадратноеуравнение.
Квадратное уравнение вида
x px q 0
2
называется приведённым (а=1).
Квадратное уравнение общего вида можно привести
к приведённому:
2
ax bx c 0 : a
b
c
x x 0
a
a
2
где
b
c
p ,q .
a
a
7. Теорема Виета.
*Теорема Виета.Если приведённое квадратное уравнение
х2+px+q=0 имеет неотрицательный
дискриминант, то сумма корней этого уравнения
равна коэффициенту при Х, взятому с
противоположным знаком, а произведение
корней равно свободному члену.
х1+х2=-p,
х1·х2=q
8. Теорема, обратная теореме Виета
*Теорема, обратная теореме Виета
Если для чисел х1, х2, p, q
справедливы формулы
х1+х2=-p,
х1·х2=q
то х1 и х2 – корни
уравнения
х2+px+q=0
9. Пусть ax2+bx+c=0 квадратное уравнение общего вида
Теорема Виета:Если квадратное уравнение общего
вида
имеет
неотрицательный
дискриминант и если х1 и х2 – корни
уравнения, то
х1 +х2=-b/a
х1 ·х2= c/a
*
Пусть ax2+bx+c=0 квадратное уравнение
общего вида
10.
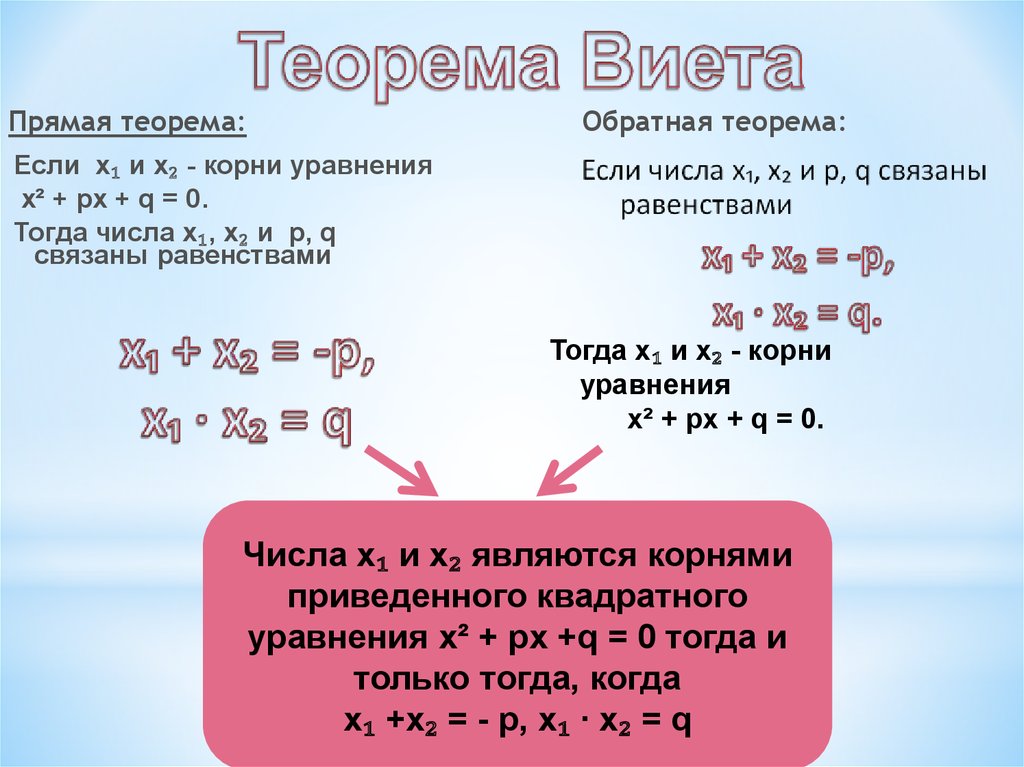
Прямая теорема:Обратная теорема:
Если х₁ и х₂ - корни уравнения
х² + px + q = 0.
Тогда числа х₁, х₂ и p, q
связаны равенствами
Тогда х₁ и х₂ - корни
уравнения
х² + px + q = 0.
Числа х₁ и х₂ являются корнями
приведенного квадратного
уравнения х² + px +q = 0 тогда и
только тогда, когда
x₁ +х₂ = - p, x₁ ∙ x₂ = q
11.
Применение теоремы ВиетаНайдите сумму и произведение корней уравнения:
у 2 41 у 371 0
х1 х2 -41
х1 х2 -371
х 210 х 0
х1 х2 210
х1 х2 0
х 15 х 16 0
х1 х2 15
х1 х2 -16
х 6 х 11 0
х1 х2 6
х1 х2 -11
2
2
2
МОУ СОШ с.Кувак-Никольское учитель
Никулкина О.А.
12. 1. Если произведение и сумма корней – положительные, то оба корня – положительные числа. 2. Если произведение корней –
Если произведение и сумма корней – положительные, то обакорня – положительные числа.
2. Если произведение корней – положительное число, а сумма
корней – отрицательное, то оба корня – отрицательные числа.
3. Если произведение корней – отрицательное число, то корни
имеют разные знаки.
А) если сумма корней – положительная, то больший по
модулю корень является положительным числом,
Б) если сумма корней меньше нуля, то больший по модулю
корень – отрицательное число
13.
Найдём корни уравнений.№
п/п
Уравнение
х2 + px + q = 0
x2
x1+x2 x1∙x2
p
q
x1
1 х2 + 5x + 6 = 0
5
6
-2
-3
-5
2 х2 – 5x - 6 = 0
-5
-6
6
-1
5
-6
3 х2 – 7x + 6 = 0
-7
6
6
1
7
6
4 х2 + x – 6 = 0
1
-6
-3
2
-1
-6
6
14.
№Уравнения
Исследование
существования
корней
1
х2-х-6=0
a>0,c<0,D>0-2
различных корня
2
3
4
5
6
7
х2+х-6=0
х2+х+6=0
х2+5х-6=0
х2+5х+6=0
х2-6х+8=0
х2-2х+3=0
a>0,c<0,D>0-2
различных корня
a>0,c>0,D<0
х1+х2
1
-1
х1·х2
х1
х2
-6
3
-2
-6
-3 2
Нет корней
a>0,c<0,D>0-2
различных корня
-5
-6
a>0,c>0,D>0
2 различных
корня
-5
6
-3
-2
a>0,c>0,D>0
2 различных
корня
6
8
4
2
a>0,c>0,D<0
-6 1
Нет корней
15. Решите уравнения
Найдите сумму и произведениекорней
х1+х2=-3+5=2
х1+х2=2+4=6
х1+х2=-3+13=10
16.
Найдите для каждого уравнениясоответствующие корни, пользуясь теоремой
Виета:
а) x2 - 2x - 3=0
x 1 = -1
x2 = 3
b) x2 - 7x + 10=0
x 1 = -5
x2 = -5
c) x2 + 12x + 32=0
x1= 5
x2 = 2
d) x2 + 3x - 18=0
x 1 = -6
x2 = 3
e) x2 + 10x + 25=0
x1= - 4
x2 = - 8
17. Определите корни квадратного уравнения, пользуясь теоремой, обратной теореме Виета:
х1 =-6, х2 =-1х1 =6, х2 =2
х1 =3, х2 =-2
х1 =16, х2 =-1
Х1 =-12, х2
=1
18.
Задача:При каком значении q уравнение
x2 6 x q 0
имеет корни, один из которых в 2 раза больше
другого?
x 2x
2
1
Решение:
По теореме, обратной теореме Виета:
Пусть
, тогда
x1 2 x1 6 3x1 6
2
x
2
x
q
1 1
2 x1 q
Ответ: при q = 8.
x1 x2 6
x1 x2 q
x1 2
q 8
2
2
2
q
19.
Окончен урок, и выполненплан.
Спасибо, ребята, огромное вам.
За то, что упорно и дружно
трудились,
И знания точно уж вам
пригодились.

















 Математика
Математика








