Цикломатика графов

1. Глава 4. Цикломатика графов

1

2.

Свойства графов, которые мы будем
изучать в данной главе, присущи графам
общего вида и не зависят от ориентации.
2

3.

4.1. Цикломатическое число
3

4.

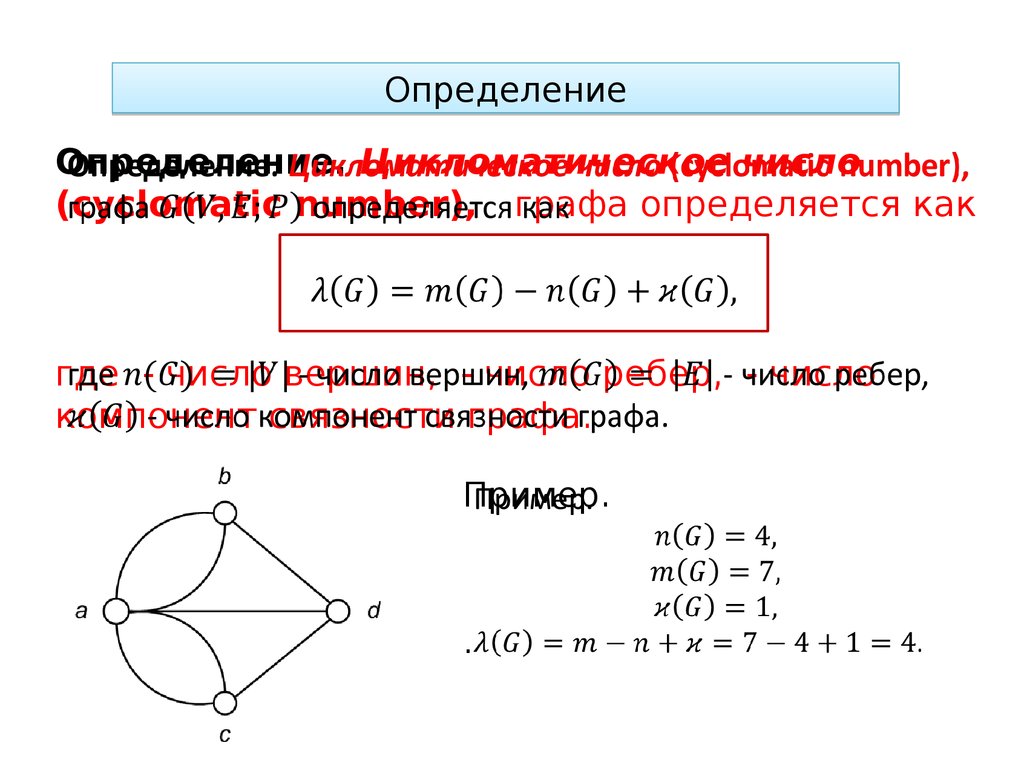
Определение
 
Определение. Цикломатическое число
(cyclomatic number), графа определяется как
где - число вершин, - число ребер, - число
компонент связности графа.
 Пример.
.

5.

Цикловые ребра и перешейки
Назовем ребро цикловым, если оно
содержится хотя бы в одном цикле; в
противном случае назовем его
перешейком (bridge).
Точкой сочленения (шарниром) называется вершина, п
удалении которой число компонент увеличивается.
 
Лемма. Пусть cуграф, полученный из
удалением ребра u. Тогда
(G ),  еслиu цикловое ребро,
(G 0)
 если u
(G ) 1,перешеек.
5

6.

 
Доказательство.
1. Пусть ребро u соединяет вершины и
входит в некоторый цикл. Если удалить
ребро , то можно построить цепь
соединяющую те же вершины и в обратном
порядке и не содержащую . Следовательно,
удаление не увеличивает числа компонент
то есть
 
2. Пусть ребро u не входит ни в какой цикл
графа . Тогда очевидно, при удалении ребра
u из любой цепи, соединяющей вершины , , в
графе не найдется ни одной цепи,
соединяющей эти же вершины
и
6

7.

Свойства цикломатического числа
 
Удаление ребра в графе может привести
только к уменьшению цикломатического
числа.
Действительно, если u – цикловое ребро, то
а если u – перешеек, то
.
(G ),  если    u  перешеек ,
(G 0)
 если u р
ебро.
(G ) 1,цикловое
7

8.

 
Теорема.
1. .
2. тогда и только тогда, когда граф не
содержит циклов.
 
Доказательство.
1. Будем удалять из графа по очереди ребра,
при этом цикломатическое число может только
уменьшиться. В конце концов получим пустой
(безреберный) граф , для которого
Отсюда
 
2. Пусть в графе нет циклов (все ребра –
перешейки). Тогда, удаляя их, мы не изменяя ,
придем к пустому графу, для которого
Наоборот, если удалять мы можем только
перешейки, так как иначе стало бы
8
отрицательным.

9.

4.2. Деревья
9

10.

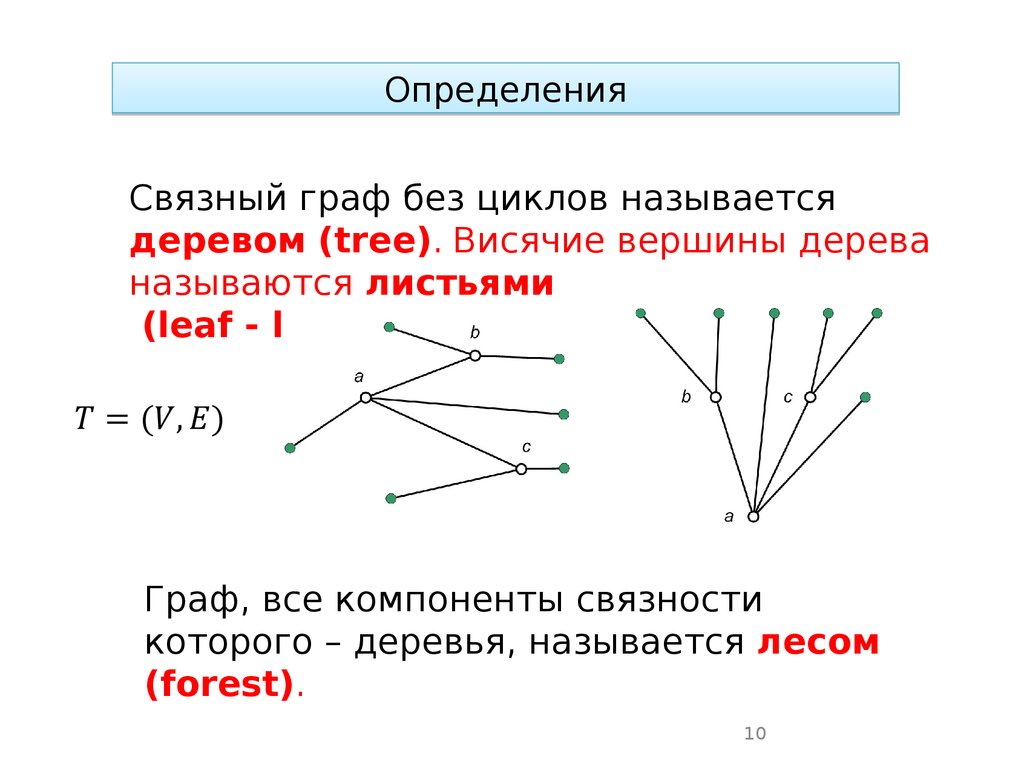
Определения
Связный граф без циклов называется
деревом (tree). Висячие вершины дерева
называются листьями
(leaf - leaves).
 
Граф, все компоненты связности
которого – деревья, называется лесом
(forest).
10

11.

Свойства дерева
 
1. (определение дерева).
2. (из определения).
3. Каждое ребро в – перешеек (т.е. при
удалении любого ребра увеличивается на
единицу).
4. Для любых двух вершин дерева существует
одна и только одна соединяющая их цепь, и
эта цепь простая.
5. Соединение любых двух вершин дерева
новым ребром приводит к появлению цикла.
6. Вершина дерева является точкой
сочленения (шарниром) тогда и только тогда,
когда ее степень .
7. Если , то в есть по крайней мере11две

12.

 
Доказательство.
Свойства 1, 2, 3 непосредственно следуют из
определения.
Свойство 4. (Доказательство от противного).
Предположим, что существуют две различные
цепи
и
cоединяющие вершину с вершиной , причем
. При этом первая из этих цепей имеет
ненулевую длину. Тогда ребро , где
(если и при , то положим является цикловым,
так как после его удаления из вершины и
останутся соединенными маршрутом
.
Следовательно, граф имеет циклы, что
противоречит определению дерева. 12

13.

йство 5. Добавление ребра (разумеется, без добавлени
шины) приводит к увеличению на единицу,
сть к появлению цикла.
йство 6 проверяется непосредственно: все вершины де
ме висячих, являются точками сочленения.
йство 7. В любом графе с числом вершин 2 есть по кр
е две вершины, не являющиеся точками сочленения.
дерева это висячие вершины.
13

14.

4.3. Каркасы
14

15.

Определение
 
Определение. Всякий суграф графа , у
которого
называется каркасом графа (синонимы: óстов,
стягиваюшее дерево, spanning tree, ST).
Каркас связного графа является деревом.
 Поскольку
– суграф, то и
Отсюда
15

16.

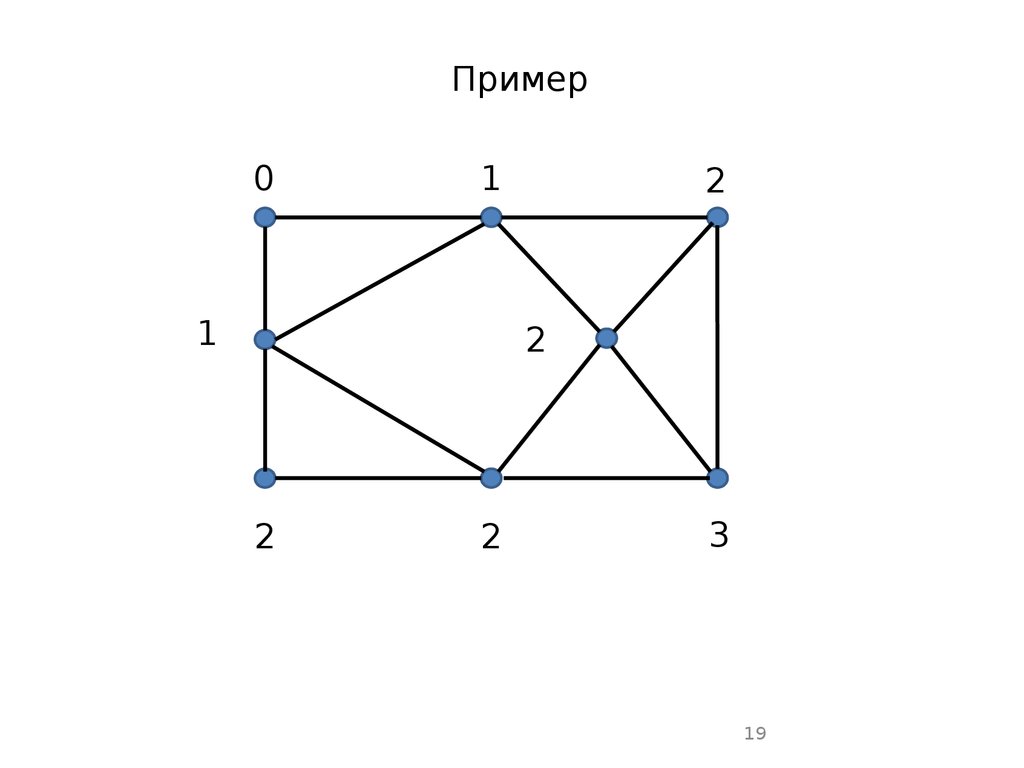
Алгоритм нахождения каркаса
Алгоритм является модификацией
волнового алгоритма нахождения
кратчайшей цепи.
Шаг 1. Выберем произвольную
вершину и пометим ее меткой 0.
Шаг 2. Все непомеченные вершины,
смежные с вершинами, имеющими
метку k, помечаем меткой k + 1.
Разметка продолжается
до тех пор, пока все вершины не будут
помечены. При такой разметке метки
смежных вершин не могут отличаться
16
более чем на

17.

 
Шаг 3. После окончания разметки будем
просматри-вать вершины в любом порядке
и удалять некоторые ребра по следующим
правилам:
• если в данный момент мы находимся в
вершине с меткой то удаляем все ребра,
которые соединяют с вершинами,
имеющими ту же метку;
• из ребер, соединяющих с вершинами,
имеющими метку , удаляем все, кроме
любого одного.
17

18.

 
Покажем, что суграф , оставшийся
после такого удаления ребер, является
каркасом графа .
1. так как правила удаления таковы, что
разметка сохраняется и для суграфа .
Поэтому число вершин, соединимых с
вершиной, имеющей метку 0, одинаково в
T и в G.
2. Разметка такова, что ребро между
двумя вершинами с одинаковыми метками
– цикловое. Далее, мы отыскиваем для
каждой вершины единственную цепь,
соединяющую эту вершину с вершиной,
имеющей метку 0, отсекая все другие
возможные цепи.
18

19.

Пример
0
1
1
2
2
2
2
3
19

20.

Кратчайший каркас графа
 
Рассмотрим связный обыкновенный граф со
взвешенными ребрами ; вес ребра обозначим
через Если ребра нет, то .
Задача заключается в том, чтобы из всех
каркасов графа найти такой, что сумма весов
его ребер – наименьшая. Такой каркас
называется кратчайшим (shortest spannig
tree – SST). Задача нахождения SST возникает,
если какие-либо пункты нужно связать
кратчайшей сетью коммуникаций
(трубопроводов, электрических проводов,
дорог и т.д.). Задача нахождения кратчайшего
каркаса – это одна из немногих задач теории
графов, которую можно считать полностью
20
решенной.

21.

Алгоритм Прима
 
Идея алгоритма состоит в постепенном
выращивании кратчайшего стягивающего
дерева из любой началь-ной вершины.
Пусть на некоторой итерации имеется
дерево Множество его вершин обозначим .
Тогда - множество вершин графа, не
принадлежащих дереву Найдем
кратчайшее ребро, соединяющее
множества и и добавим это ребро к дереву
Многократно выбирая кратчайшие ребра, в
конце концов получим SST.
21

22.

Robert C. Prim (b. 1921) along with
coworker Joseph Kruskal developed two
different algorithms (see greedy algorithm)
for finding a minimum spanning tree in a
weighted graph, a basic stumbling block in
computer network design. His self-named
algorithm, Prim's algorithm, was originally
discovered in 1930 by mathematician
Vojtěch Jarník and later independently by
Prim in 1957. It was later rediscovered by
Edsger Dijkstra in 1959. It is sometimes
referred to as the DJP algorithm or the
Jarník algorithm
en.wikipedia.org/wiki/Robert_C._Prim
22

23.

 
Алгоритм Прима нахождения SST очень похож
на алгоритм Дейкстры нахождения кратчайшей
цепи в графе. Точно так же происходит разметка
вершин временными и постоянными метками,
однако правило обновления меток несколько
отличается: при обнаружении вершины для
которой В результате постоянная метка при
вершине дает длину кратчайшего ребра,
соединяющего данную вершину с уже
построенным каркасом. Еще одно отличие состоит
в том, что построение кратчайшего каркаса
происходит не после окончания, а в процессе
разметки. При превращении временной метки в
постоянную сразу же происходит добавление
очередного ребра к растущему каркасу. На это
ребро указывает обратная навигационная
ссылка
23

24.

 
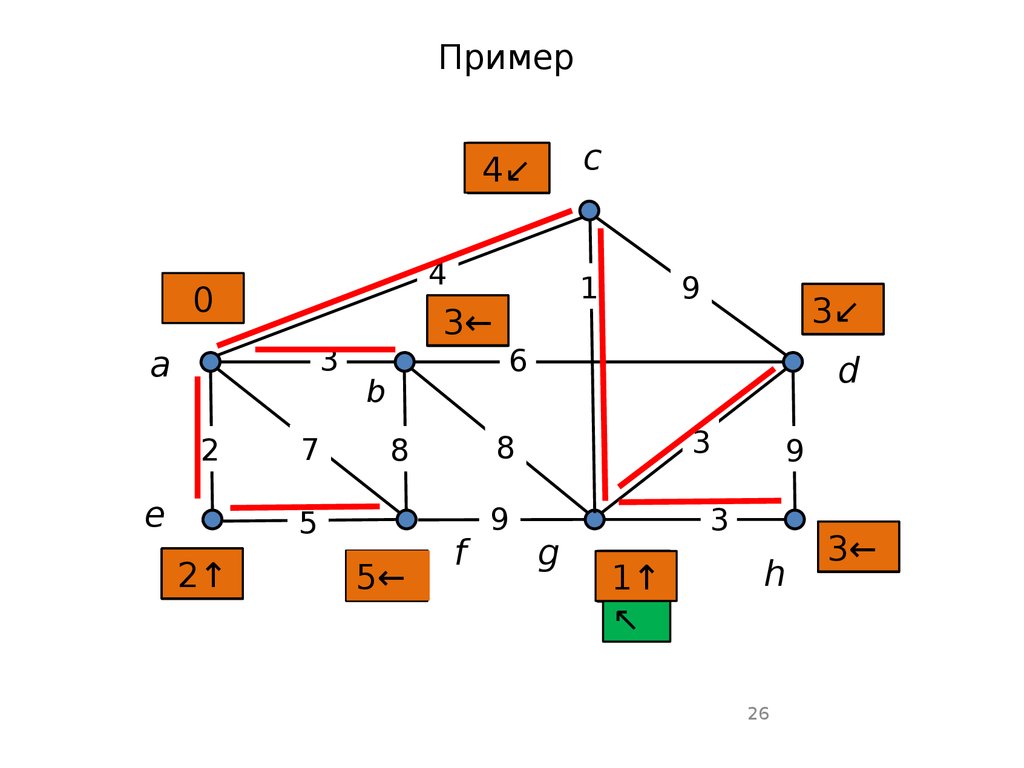
Шаг 0. Инициализация.
Назначить любой исходной вершине s метку и
считать ее постоянной. Вершины с постоянными
метками считаются обработанными и к ним
алгоритм не возвращается. Для всех назначить
метки и считать эти метки временными.
Текущая вершина
 
Шаг 1. Обновление соседних временных
меток из текущей вершины.
Взять текущую вершину
Рассмотреть все смежные с ней вершины
с временными метками и, если то обновить их
по правилу: . При обновлении меняется и
навигационная метка: она дает ссылку на
вершину из которой произошло обновление.
24

25.

 
Шаг 2. Превращение метки в постоянную.
а) Среди всех вершин с временными метками
найти вершину с наименьшей меткой.
б) Считать эту метку постоянной.
в) Считать эту вершину текущей
г) Ребро, указанное навигационной меткой,
включить в каркас.
г) Если есть еще временные метки, возврат на
шаг 1.
д) Если все метки постоянные – переход на
шаг 3.
Шаг 3. Найден кратчайший каркас.
25

26.

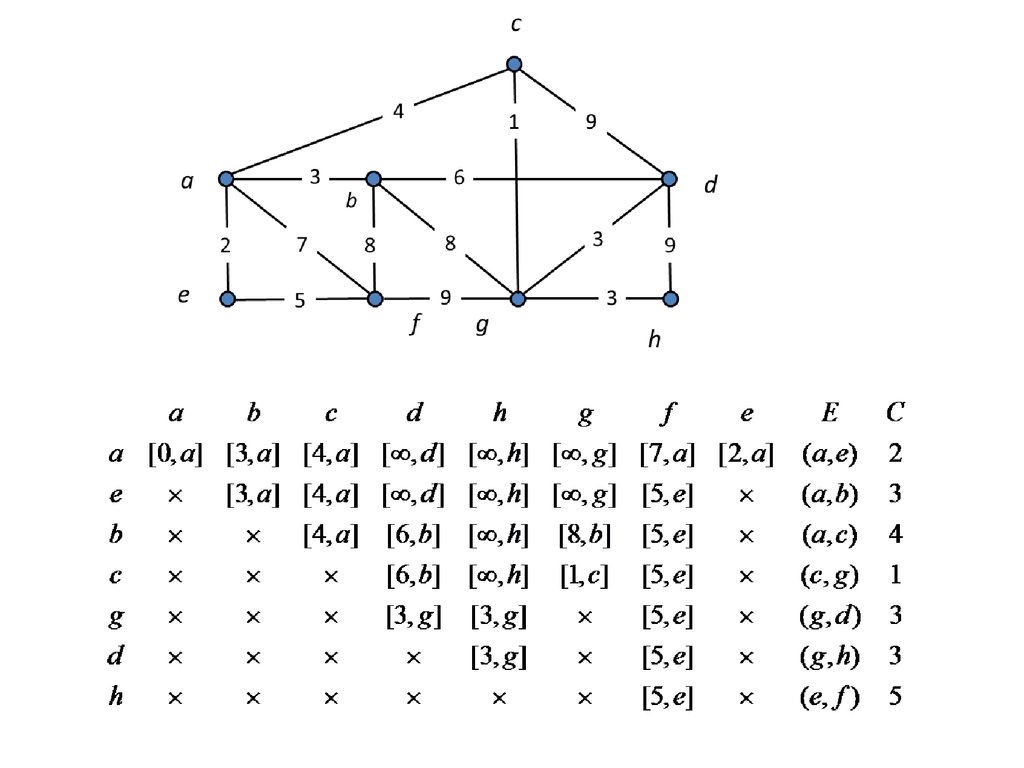
Пример
c
 4↙
4
0
 
3←
3
a
2
e
7
9
 3↙
6←
6
b
 5←
7↖
5←
d
3
8
8
5
 2↑
1
f
9
g
9
3
 1↑
8
h
↖
26
 
3←

27.

27

28.

Теорема о хорде каркаса
 
Ребра графа G, не принадлежащие его
каркасу , называются хордами каркаса
в.
Число хорд каркаса равно
цикломатическому числу графа.
Действительно:
Вычитая из первого равенства второе и
учитывая, что
получаем
28

29.

 
Теорема. Пусть – некоторый
произвольный каркас графа , –
произвольная хорда этого каркаса. Тогда в
графе существует цикл, содержащий и не
содержащий других хорд каркаса , причем
этот цикл простой и единственный.
 
Д о к а з а т е л ь с т в о . Доказательство
проводится для связного графа, т.к. для
несвязного графа можно провести
доказательство для каждой из компонент.
Пусть – те вершины графа , которые
соединяет ребро . Так как – дерево, то в
нем имеется единственная цепь, притом
простая, соединяющая с (свойство
дерева) и эта цепь вместе с хордой
образует тот самый единственный простой
29
цикл.

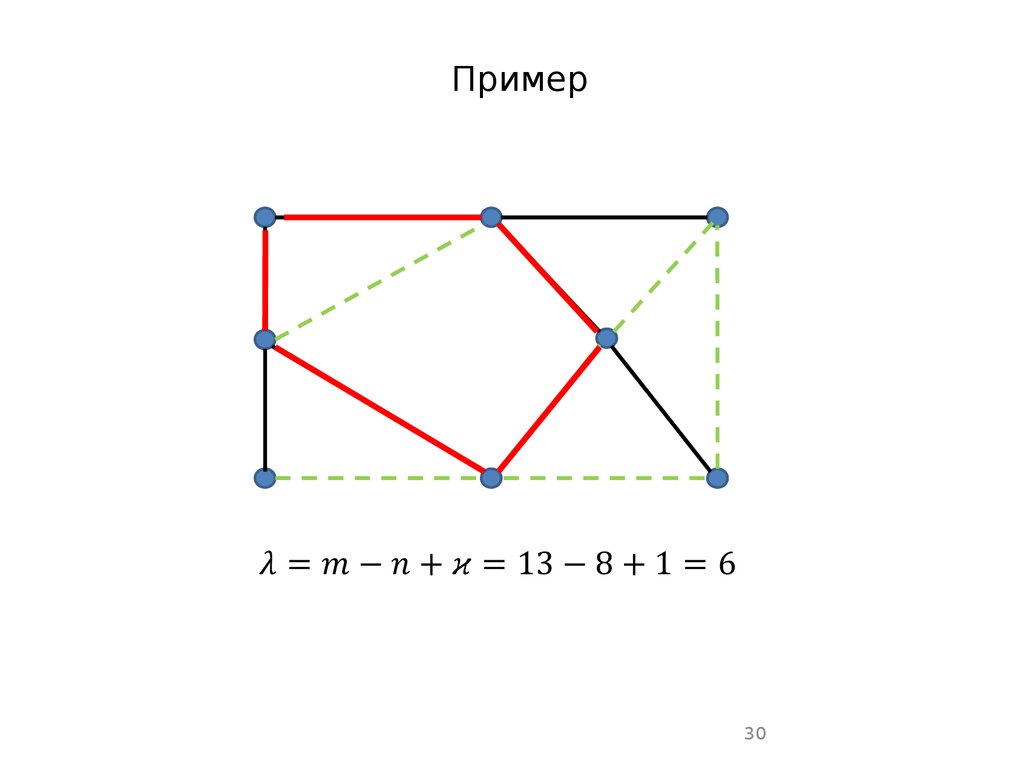
30.

Пример
 
30

31.

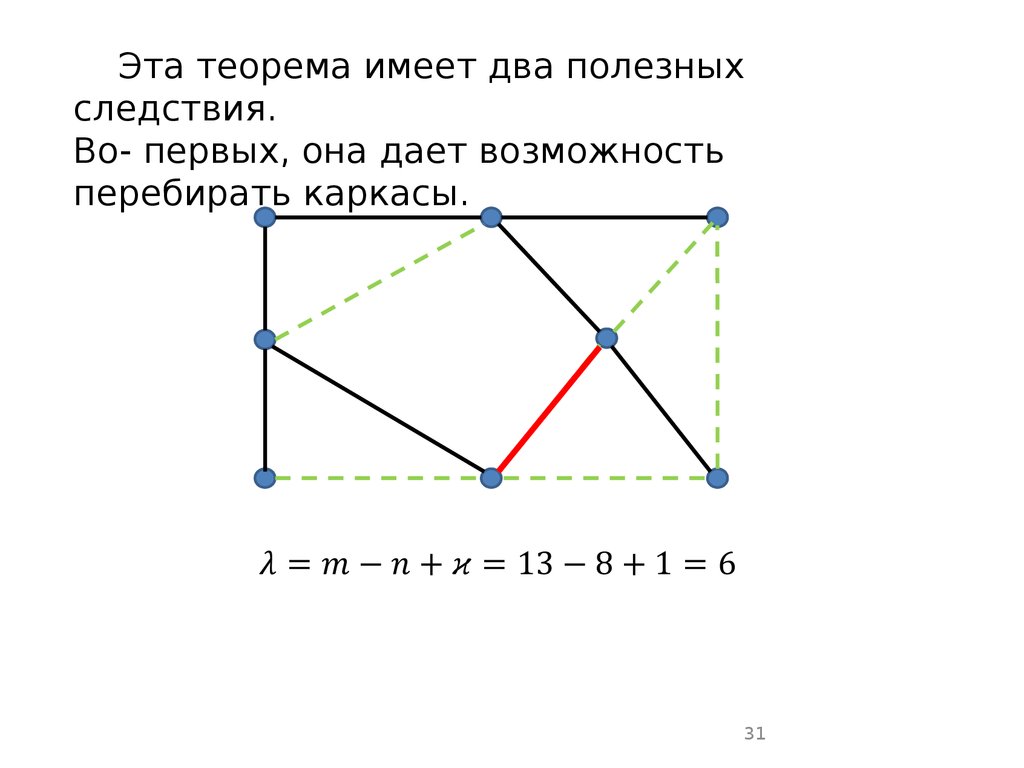
Эта теорема имеет два полезных
следствия.
Во- первых, она дает возможность
перебирать каркасы.
 
31

32.

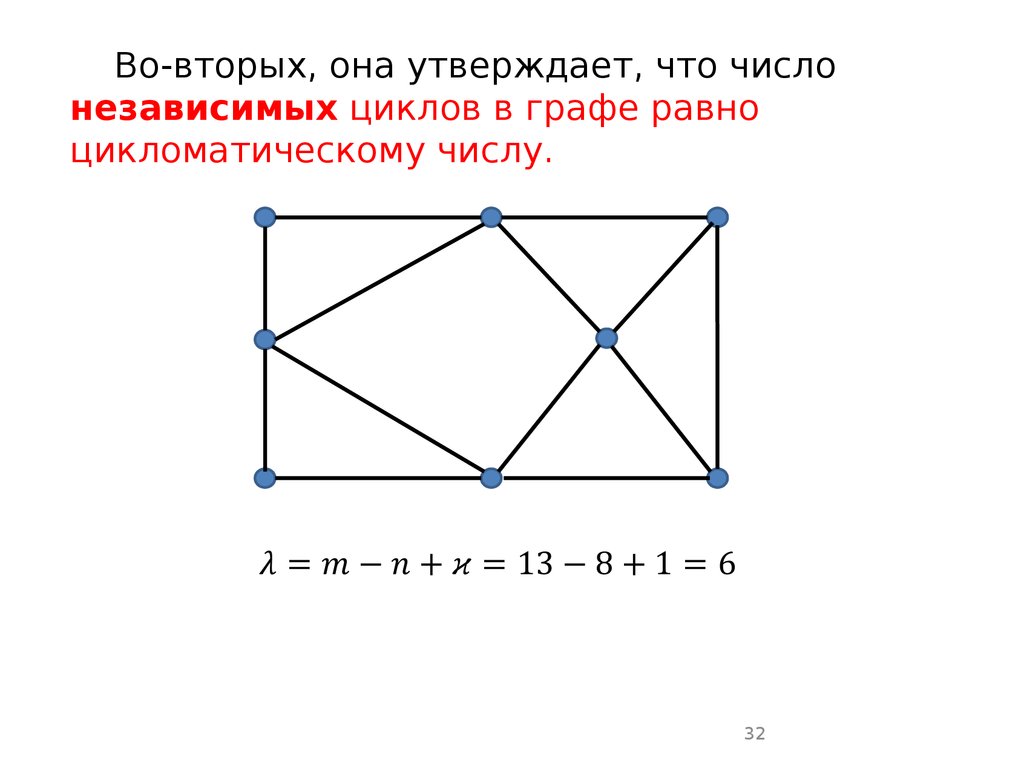
Во-вторых, она утверждает, что число
независимых циклов в графе равно
цикломатическому числу.
 
32

33.

дому суграфу G ’=(V,E ’) графа G=(V,E) взаимно однознач
тветствует подмножество ребер E ’ E ; каждое E ‘ задает
тором
a(G )  a  ( E ') (a1 , a2 , , am ), у которого
 
1, если  ui   E
ai    
  .
  E
0, если  ui
алее суграфом называют и E ‘, aи( E ').
 
еделяется
операция сложения суграфов , :
()\() (симметрическая разность).
векторов, соответственно, покомпонентное сложение
одулю два (исключающее или)
(a1 , a2 , , am ) (b1 , b2 , , bm ) ( a1 b1 , a2 b2 , , am bm )
0 0=0, 1 0=1, 0 1=1, 1 1=0
33

34.

Однореберные суграфы
r
r
r
e1 (1,0, ,0), e2 (0,1, ,0), , em (0,0, ,1)
но независимы, а любой суграф есть их линейная комби
r
r
r
(a1 , a2 , , am ) a1e1 a2 e2 am em .
 Множество
суграфов данного графа G образуeт
линейное пространство со сложением , и обычным
умножением; нуль-вектор =(0,0,…,0) соответствует E
’= ; обратный элемент для
каждого суграфа– он сам: = . Базис пространства
суграфов
размерности
m есть
множество
однореберных
Пример: сумма
суграфов
(1,1,0,1)
суграфов.
(1,0,1,1)=(0,1,1,0)
=
34

35.

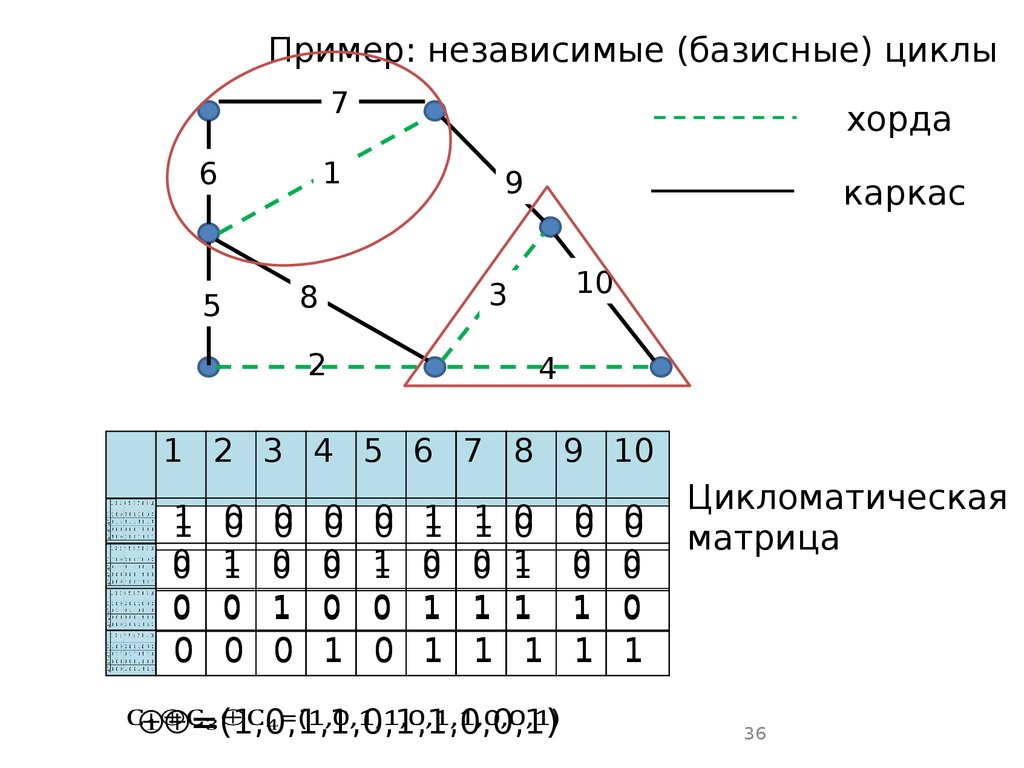
ом разделе цикл определяется как суграф, все вершины
го имеют четные валентности. Сумма двух циклов есть ц
бязательно цикл в обычном понимании: это могут быть д
а без общих вершин). Множество циклов образует линей
транство.
ь теперь T -- некоторый каркас графа G. Каждой хорде э
аса поставим в соответствие тот единственный цикл, кот
образует вместе с некоторыми ребрами T, и тем самым п
систему из (G ) циклов. Элементы этой системы линейно
симы и образуют базис пространства циклов размерности
й другой цикл может быть получен как линейная комби
висимых (базисных) циклов.
35

36.

Пример: независимые (базисные) циклы
7
хорда
1
6
9
2
 
10
3
8
5
каркас
4
1 2 3 4 5 6 7 8 9 10
 1
 1  0
 0  0
 0  0
 0  0
 0  1
 1  1
 1 0 
0   0
 0  0
 0
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
0
1
0
0 1
1
1 1
0
0
1
0
0
0
Цикломатическая
матрица
 0  0 0  1  0  1  1  1  1  1
  =(1,0,1,1,0,1,1,0,0,1)
36