Связность графов

1. Глава 2. Связность графов

1

2.

2.1. Маршруты, цепи, циклы

3.

Маршруты
 Определения.
Конечная последовательность
вершин и ребер V, E
в которой соседние ребра имеют общую вершину,
называется маршрутом из вершины в вершину ,
или маршрутом, соединяющим с .
В случае маршрут называется циклическим.
Число называется длиной маршрута. Маршрут не
является частью графа, так как порядок его
обхода существенен.
Понятие маршрута не зависит от ориентации
ребер.

4.

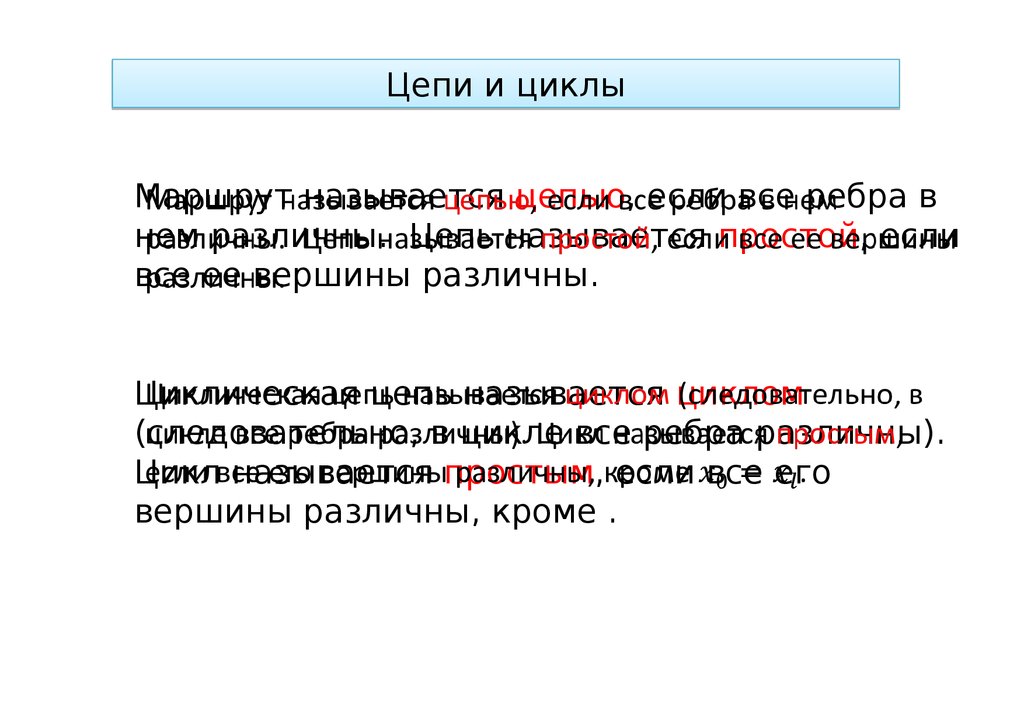
Цепи и циклы
 Маршрут
называется цепью, если все ребра в
нем различны. Цепь называется простой, если
все ее вершины различны.
Циклическая цепь называется циклом
(следовательно, в цикле все ребра различны).
Цикл называется простым, если все его
вершины различны, кроме .

5.

Лемма. Всякий маршрут графа содержит
хотя бы одну простую цепь, соединяющую ту
же пару вершин.
Доказательство
 
Если в полученном маршруте есть еще
повторяющиеся вер-шины, то снова заменяем
его более коротким и так далее, пока не
выделим маршрут без повторяющихся вершин.

6.

Пример
c
4
2
a
aф
1
d
3
b
5
e
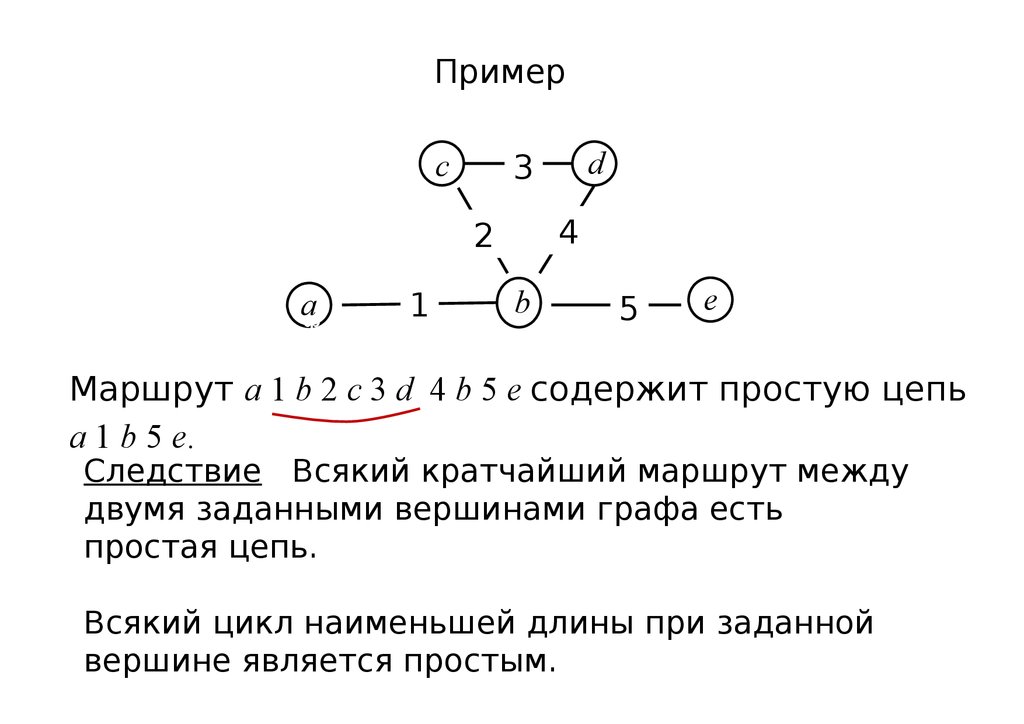
Маршрут a 1 b 2 c 3 d 4 b 5 e содержит простую цепь
a 1 b 5 e.
Следствие Всякий кратчайший маршрут между
двумя заданными вершинами графа есть
простая цепь.
Всякий цикл наименьшей длины при заданной
вершине является простым.

7.

Если маршрут рассматривать с учетом ориентации
ребер (может быть и по звеньям), то получим
соответствующие определения:
ориентированный маршрут (ормаршрут);
ориентированная цепь (орцепь) – путь;
простая орцепь – простой путь.

8.

Задачи о маршрутах
В теории рассматривается ряд задач и алгоритмов
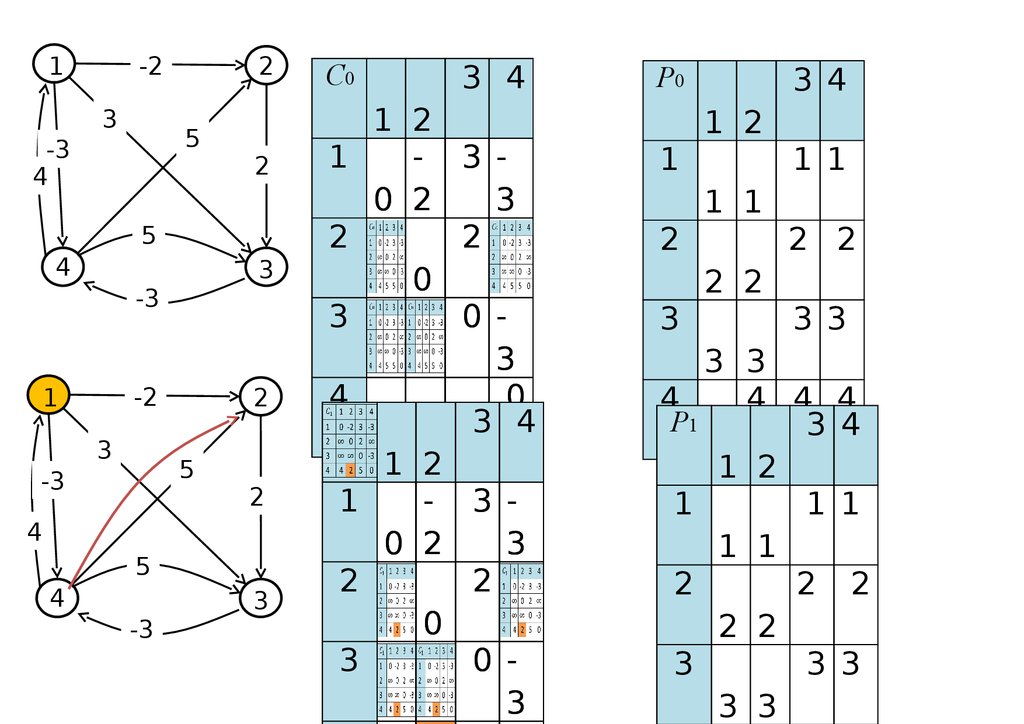
определения свойств маршрутов:
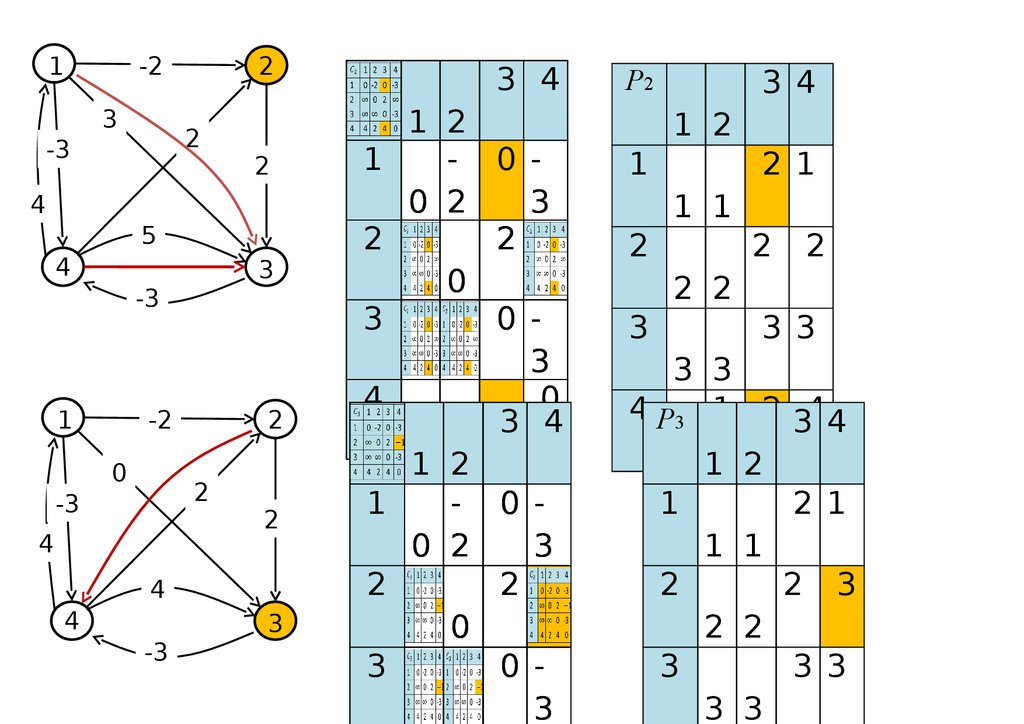
существование маршрутов заданной длины;
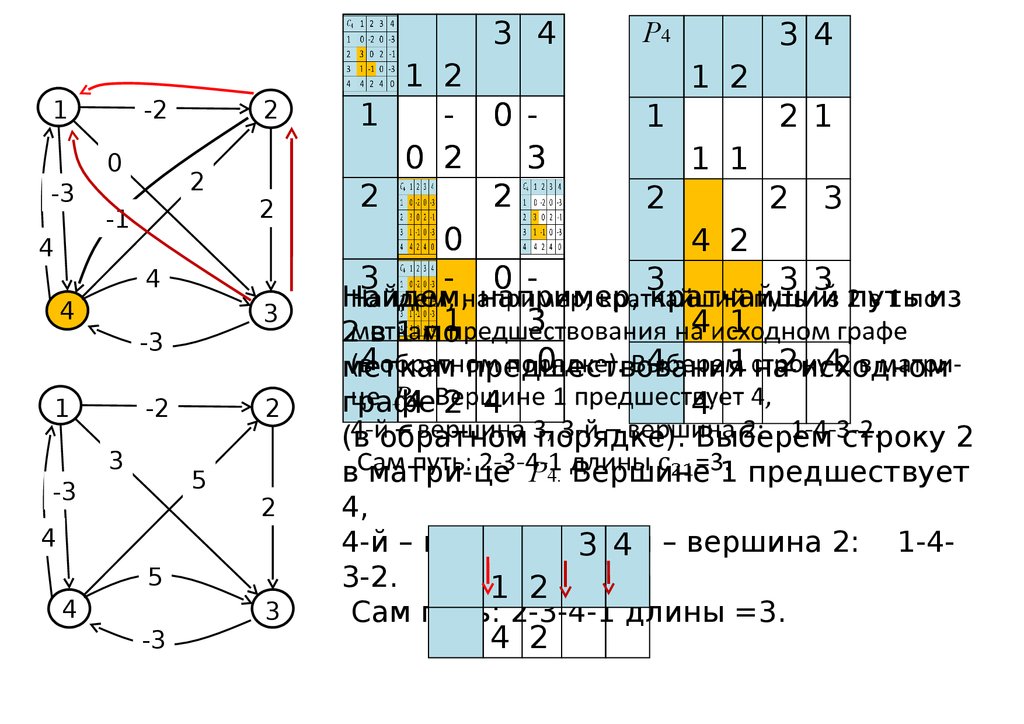
достижимость вершин;
число маршрутов заданной длины;
компоненты связности и бисвязности;
кратчайшие цепи/пути;
кратчайшие цепи/пути на взвешенных графах.

9.

Существование маршрутов
Рассматривается неориентированный (маршрут не
предполагает ориентации) униграф (важен лишь
факт
вершин).
Такойсмежности
граф можно
рассматривать как
симметричное бинарное отношение и его можно
задать матрицей смежности R, элементы rij которой
– булевы. rij=1, если вершины смежны; из вершины xi
 
существует маршрут
длины 1 в вершину xj.
Элемент матрицы R2
определяет существование
шрута длины 2 между этими вершинами. Далее по индукции:
 
(*)

10.

маршрут длины l из вершины xi
в вершину xj
существует, если
существует маршрут длины l-1 из вершины xi в
вершину xk
xk и xj смежны.
и вершины
Для маршрутов других видов задаются
соответствующие матрицы смежности.

11.

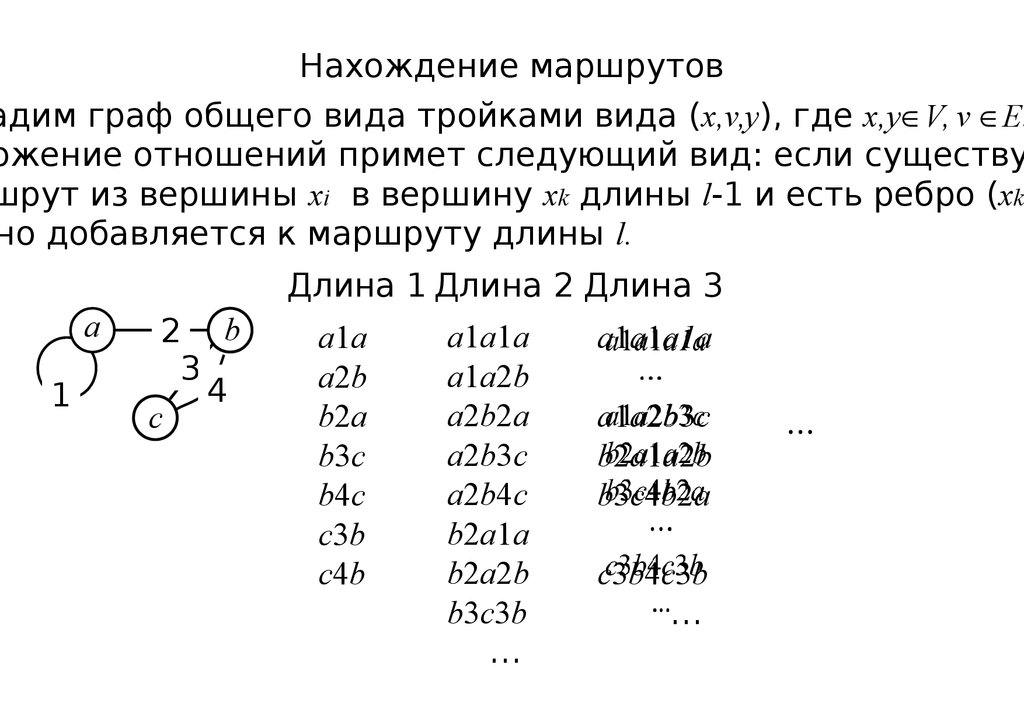
Нахождение маршрутов
адим граф общего вида тройками вида (x,v,y), где x,y V, v E.
ожение отношений примет следующий вид: если существу
шрут из вершины xi в вершину xk длины l-1 и есть ребро (xk
но добавляется к маршруту длины l.
Длина 1 Длина 2 Длина 3
a
1
2 b
3
4
c
a1a
a2b
b2a
b3c
b4c
c3b
c4b
a1a1a
a1a2b
a2b2a
a2b3c
a2b4c
b2a1a
b2a2b
b3c3b
…
 a1a1a1a
a1a2b3c
b2a1a2b
b3c4b2a
c3b4c3b
…
 

12.

Число маршрутов
 Пусть
задан граф общего вида с матрицей
смежности Элемент определяет число ребер,
соединяющих вершины и .
Возведем в l – ю степень по правилам
обычного матричного умножения и
рассмотрим
 
Теорема. равен числу различных маршрутов
длины l из вершиныв вершину
Доказательство индукцией по
 

13.

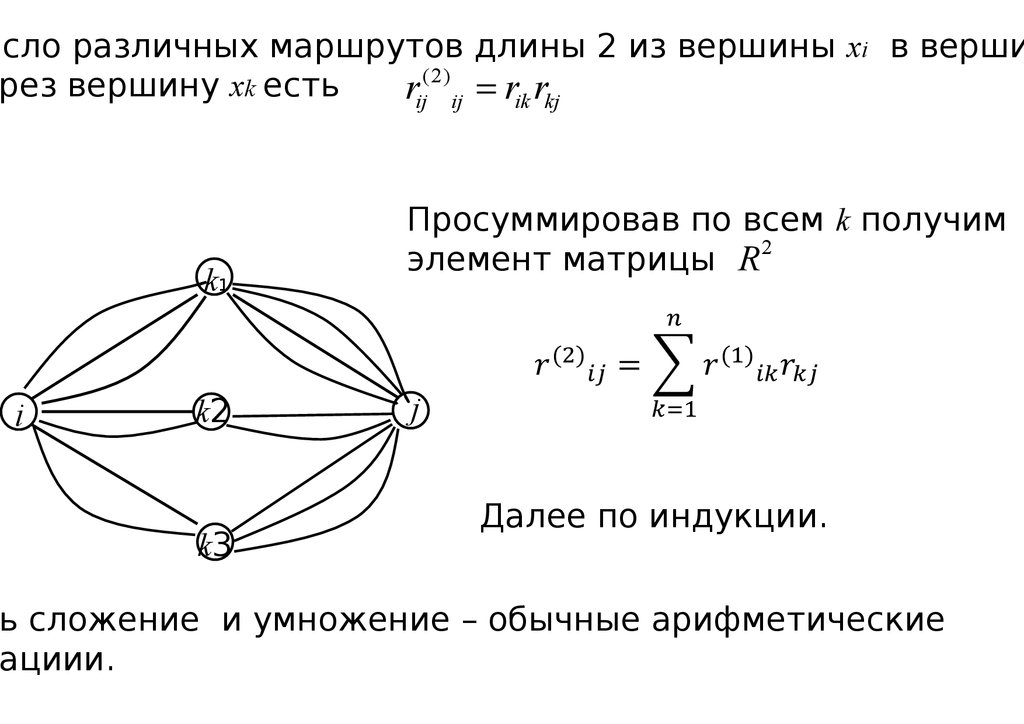
исло различных маршрутов длины 2 из вершины xi в верши
(2)
рез вершину xk есть
rij ij rik rkj
k1
Просуммировав по всем k получим
элемент матрицы R 2
 
iш
k2
k3
j
Далее по индукции.
ь сложение и умножение – обычные арифметические
ациии.

14.

a
1
2
3
b
4
5
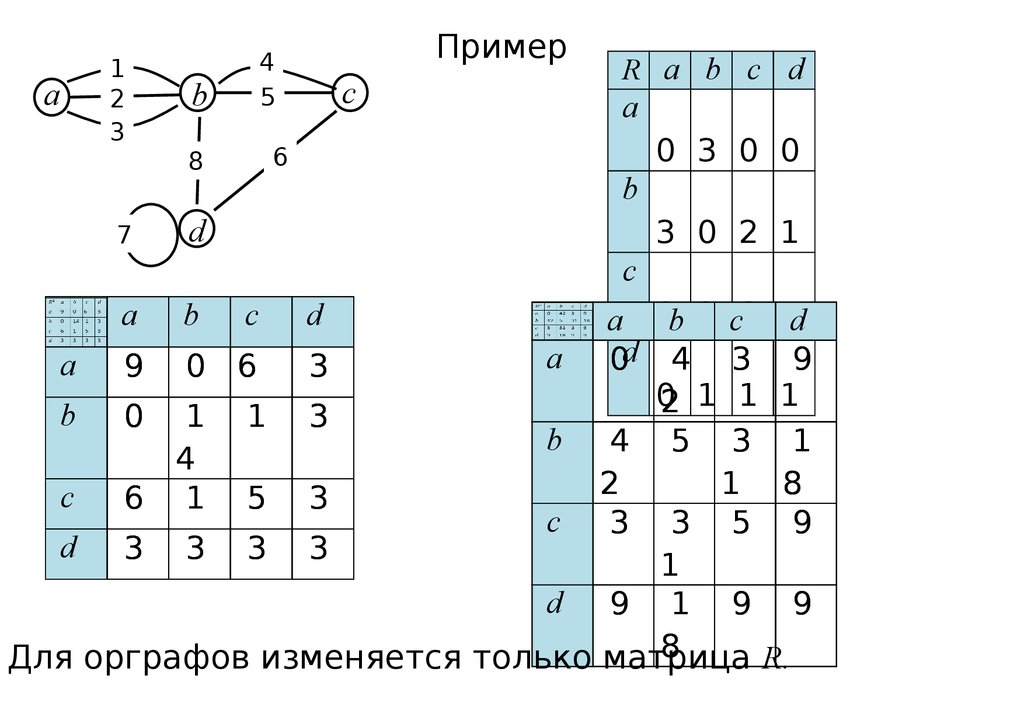
Пример
c
R a b c d
a        
0 3 0 0
6
8
b        
d
3 0 2 1
7
c        
a b c
d
a 0b 2 c0 1d
a  0d   4    3    9
a  9  0 6   3
02 1 1 1
b  0  1  1  3
b  4  5  3  1
4
2
1 8
c  6  1  5  3
c  3  3  5  9
d  3  3  3  3
1
d  9  1  9  9
8
Для орграфов изменяется только матрица
R.

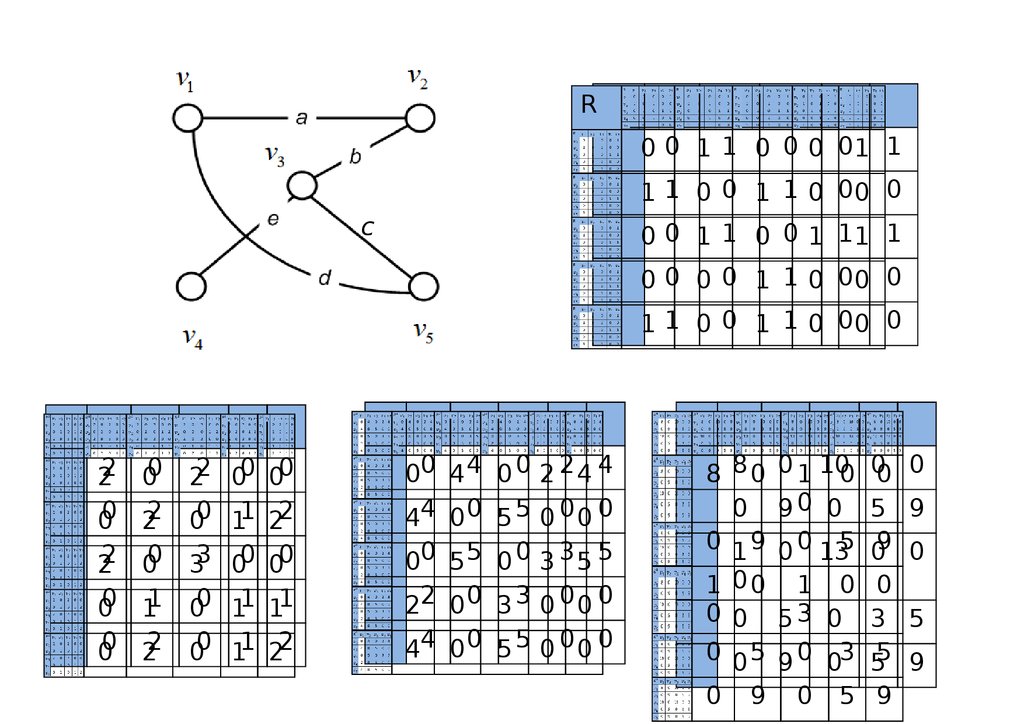
15.

RR
0 0 1 1 0 0 0 01 1
1 1 0 0 1 1 0 00 0
c
0 0 1 1 0 0 1 11 1
0 0 0 0 1 1 0 00 0
1 1 0 0 1 1 0 00 0
22
00
00
22
22
00
00
11
00
22
22 00 00
00 11 22
33 00 00
00 11 11
00 11 22
00 4 4 0 0 2 2 4 4
44 0 0 5 5 0 0 0 0
00 5 5 0 0 3 3 5 5
22 0 0 3 3 0 0 0 0
44 0 0 5 5 0 0 0 0
8 8 0 0 1 100
0 90 0
0 1 9 0 0 135
1 00 1 0
0 0 53 0
0 0 5 9 0 03
0
9
0
00 0
5 9
09 0
0
3 5
55 9
5 9

16.

Достижимость
 Если
нас интересует только достижимость
й вершины из за шагов, то есть наличие
маршрута длины то операцию сложения в
формуле умножения матриц следует слегка
модифицировать , положив определяющее
соотношение 1+1=1.
Тем самым мы определяем матрицу
смежности над булевой алгеброй
При этом элемент матрицы будет равен 1,
если существует хотя бы один маршрут
длины из вершины в вершину и 0, если не
существует ни одного такого маршрута.

17.

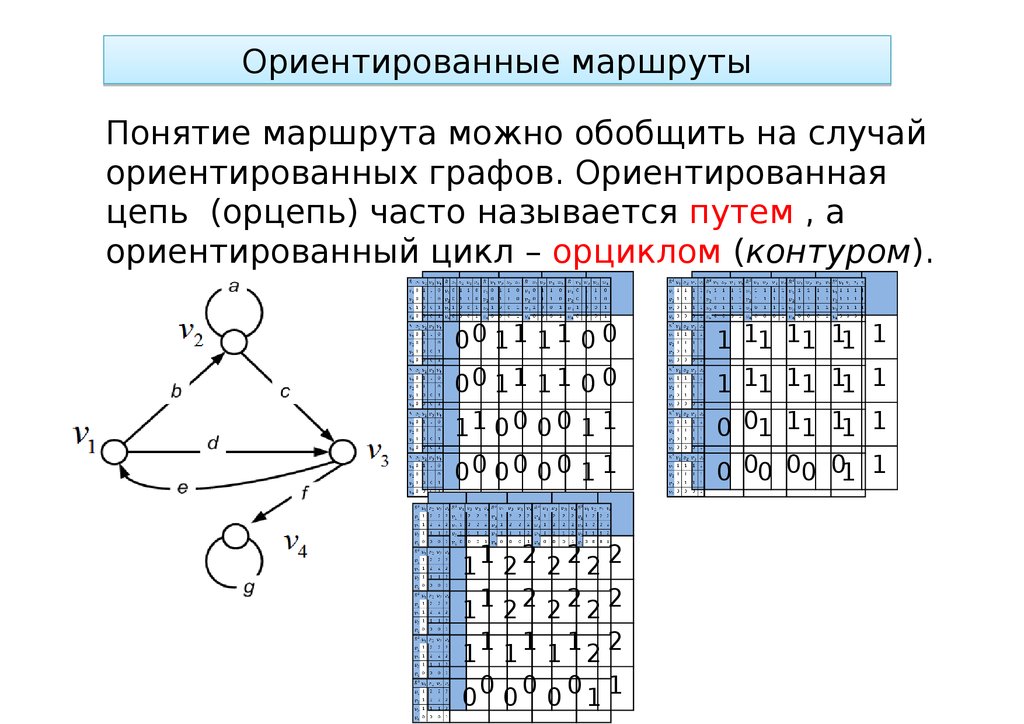
Ориентированные маршруты
Понятие маршрута можно обобщить на случай
ориентированных графов. Ориентированная
цепь (орцепь) часто называется путем , а
ориентированный цикл – орциклом (контуром).
00 1 1 1 1 0 0
1 11 11 11 1
00 1 1 1 1 0 0
1 11 11 11 1
11 0 0 0 0 1 1
0 01 11 11 1
00 0 0 0 0 1 1
0 00 00 01 1
11 2 2 2 2 2 2
11 2 2 2 2 2 2
11 1 1 1 1 2 2
0
0
0
0
0 1
0 1

18.

2.2. Компоненты связности

19.

Компоненты и бикомпоненты
 
Определение. Вершины , графа
называются отделенными , если в не
существует никакой соединяющей их
цепи, и неотделенными, если хотя бы
одна такая цепь существует.
Отношение неотделенности (связности)
вершин
• рефлексивно (каждая вершина
соединена с собой цепью нулевой
длины);
• симметрично (цепь, записанная в
обратном порядке – тоже цепь);
• транзитивно (если существует цепь из

20.

 
Таким образом, отношение неотделенности
есть отношение эквивалентности на
множестве вершин V; при этом разбивается
на классы попарно неотделенных вершин .
Определение. Подграфы порожденные
подмножествами, не имеют общих вершин
и ребер и называются компонентами
связности (или просто компонентами).
Число их обозначается через (G) (каппа).
Если (G) = 1, то граф называется связным.
Другая крайность – пустой граф: для него
(G) = n.
шение «быть в одной компоненте » для ребер – эквивалент
для вершин.

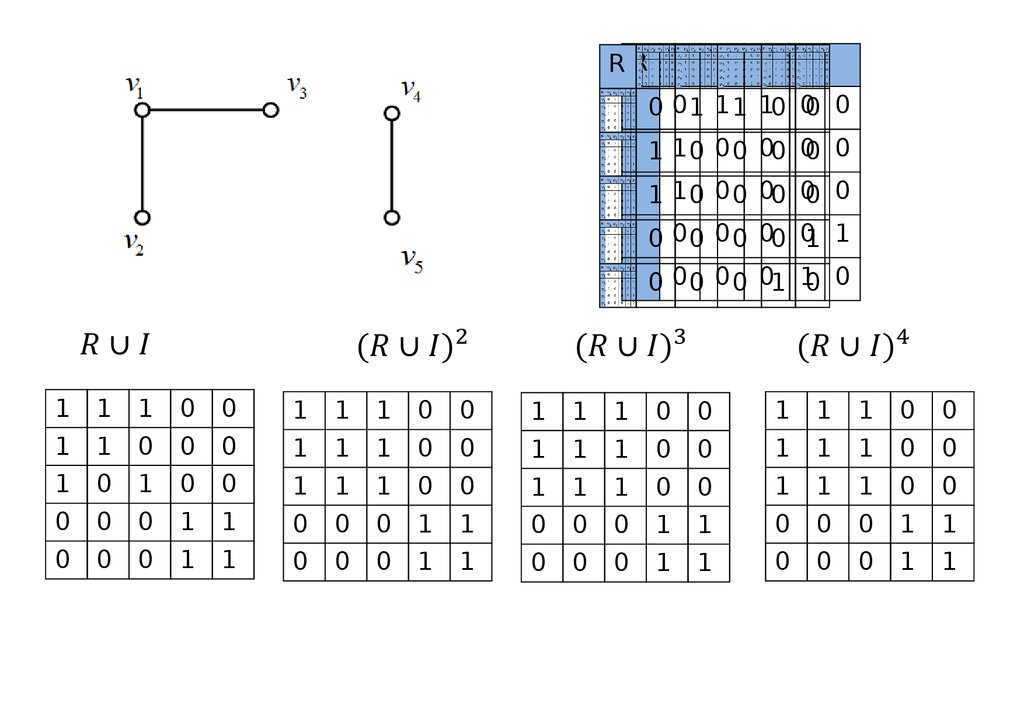
21.

RR
0 0 1 1 1 10 00 0
1 1 0 0 0 00 00 0
1 1 0 0 0 00 00 0
0 0 0 0 0 00 01 1
0 0 0 0 0 01 10 0
 
 
 
 
1
1
1
0
0
1
1
1
0
0
1
1
1
0
0
1
1
1
0
0
1
1
0
0
0
1
1
1
0
0
1
1
1
0
0
1
1
1
0
0
1
0
1
0
0
1
1
1
0
0
1
1
1
0
0
1
1
1
0
0
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1
0
0
0
1
1

22.

Для ориентированных графов
 
Вершина y достижима из вершины x, если
существует путь из в Вершины x и y
взаимодостижимы , если истинно высказывание
Отношение взаимодостижимости рефлексивно,
симметрично и транзитивно, т.е. является
отношением эквивалентности. Множество вершин
графа разбивается на классы взаимодостижимых
вершин.
Определение. Подграфы, порожденные этими
подмножествами называются компонентами
бисвязности, или бикомпонентами графа .
Граф называется сильно связным, если он состоит

23.

ожество вершин, достижимых из вершины x, обозначим Д(x).
орема Вершины x и y взаимодостижимы тогда и только
гда, когда Д(x) = Д(y).
Если x и y взаимодостижимы, то для любой вершины z V
иду транзитивности отношения взаимодостижимости,
z Д(x) следует z Д(y), а из z Д(y) следует z Д(x),
этому Д(x) = Д(y).
Пусть Д(x) = Д(y). Так как x Д(x) и y Д(y), то из равенства
) = Д(y) следует, что y Д(x) и x Д(y), т.е. вершины x и y
аимодостижимы.

24.

 
ица
смежности R над булевой алгеброй B{0,1} рефлексивн
I, I – единичная матрица), т.к. любая вершина связна сама
ой и достижима сама из себя. Для неориентированного гра
етрична.
шение неотделенности/доcтижимости – это транзитивное
кание отношения смежности
 
=R
 
мент
матрицы ij =1, если существует цепь/путь из вершины xi
ршину xj. Для нахождения применяется итеративная процед
первой итерации положим R1:=R; далее итеративно
Rl+1:=Rl Rl Rl (l – индекс итерации)
ь операция -- это , -- произведение отношений
риц). На некоторой итерации Rl+1= Rl и процесс останавливае
этом .

25.

Алгоритм работает «на месте» -- матрица Rl+1
записывается на месте матрицы R.
 [i,j]:
=[i,j] [i,k] [k,j]

26.

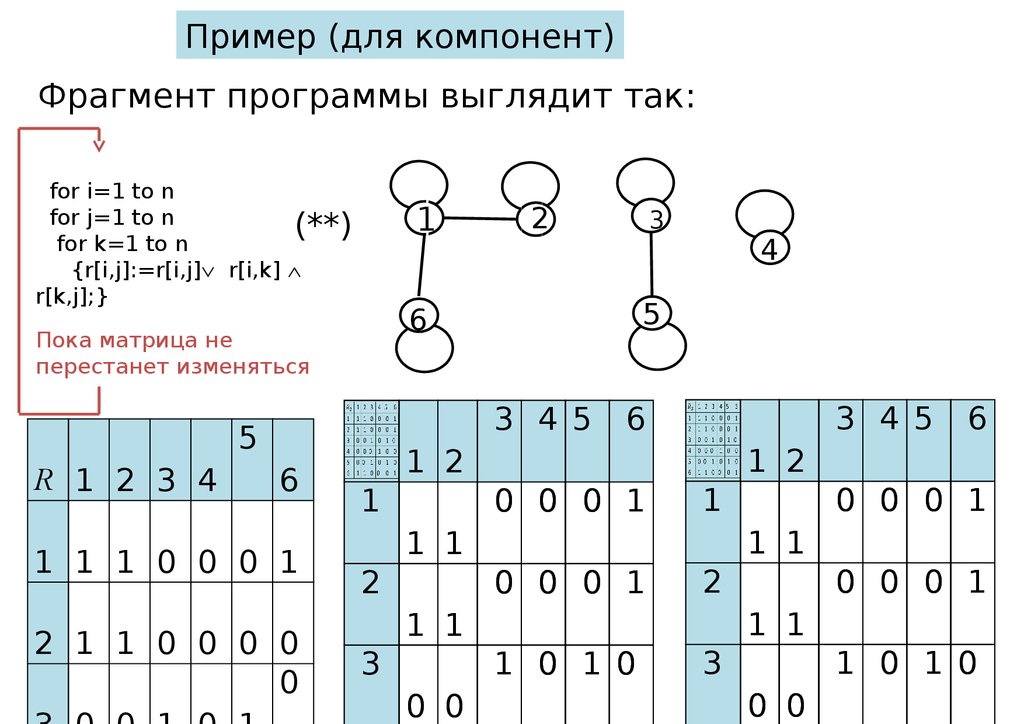
Пример (для компонент)
Фрагмент программы выглядит так:
for i=1 to n
for j=1 to n
(**)
for k=1 to n
{r[i,j]:=r[i,j] r[i,k]
r[k,j];}
Пока матрица не
перестанет изменяться
 
R
 
1
 
2
 
 
1
 
1
 
1
 
 
2
 
1
 
1
 
 
3
 
0
 
0
 
 
4
 
0
 
0
 
5
 
 
0
 
0
 
 
6
 
1
 
0
0
1
11
1
1
2
4
5
6
 
1
 1  
1
 2  
1
 3  
0
3
 
2
 
1
 
1
 
0
 3  4 5   6
 0  0  0  1
 0  0  0  1
 1  0  1 0 
 
1
 1  
1
 2  
1
 3  
0
 
2
 
1
 
1
 
0
 3  4 5   6
 0  0  0  1
 0  0  0  1
 1  0  1 0 

27.

 Компоненты
связности образуют множества
={1,2,6}, ={3,5},
={4}. Вершинам одной компоненты соответствуют
одинаковые
строки матрицы Rl+1= .

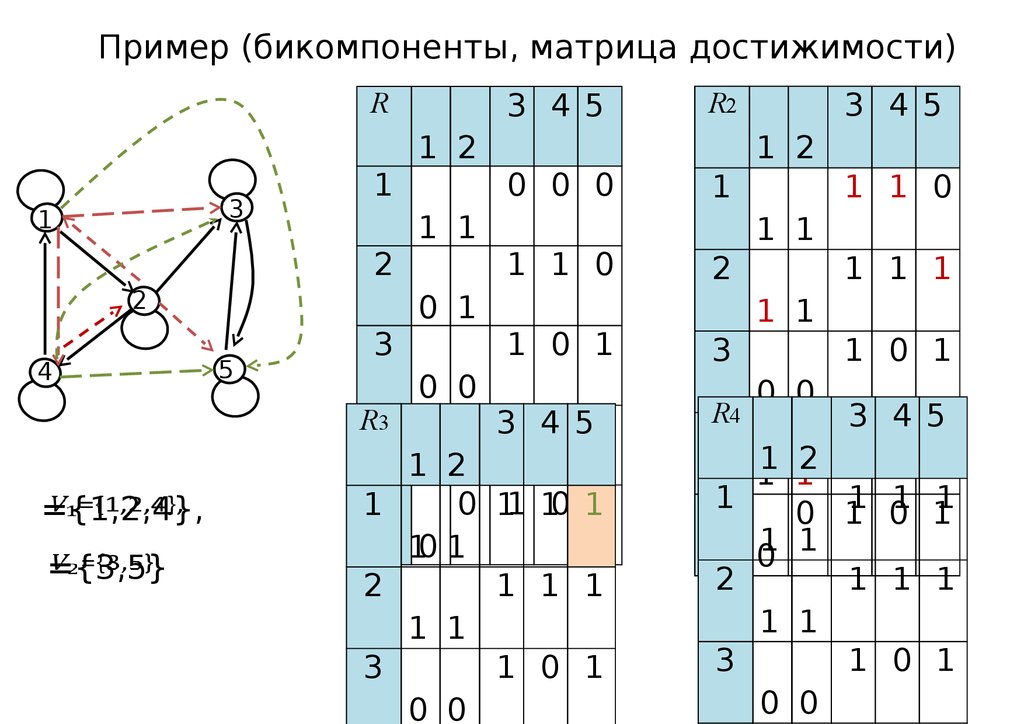
28.

Пример (бикомпоненты, матрица достижимости)
R
3
1
 1
 2
2
4
5
 3
R
 43
 
={1,2,4},
 
={3,5}
 5
 1
 2
 3
     3  4 5 
1 2
     0  0  0
1 1
     1  1  0
0 1
     1  0  1
0 0
       3
0   4
 1 5 
 0
11 20
 1  1
 0  1
 1
    0  1
10 1 
     1  1  1
1 1
     1  0  1
0 0
R2    
 1
 2
 3
R4
 4
 1
 5
 2
 3
1
 
1
 
1
 
0
  
1
1
  
1
0
 
1
 
0
2
 
1
 
1
 
0
  
2
1
 
0
 1
 
1
 
0
 3  4 5 
 1  1  0
 1  1  1
 1  0  1
 3  1
 4  0
5 
0 
 1  0
 1  1
 1
 1
 1  1  1
 1  0  1

29.

 
жность
этого алгоритма O(). Сложность умножения матриц
авляет O() и число итераций имеет порядок n.
оршалл (1962 г.)предложил алгоритм нахождения транзитив
ания сложности O(). Экономия достигается за счет изменени
ка просмотра троек вершин в цикле (**).
улевой итерации =R
(.
Фрагмент программы:
 
На
k-м
шаге цикла по k (k – индекс итерации
for k=1 to n
[i,j] =[i,j] [i,k] [k,j]
for i=1 to n
(***)
существует путь из вершины
for j=1 to n
{r[i,j]:=r[i,j] r[i,k] , проходящий через вершины с номерами, н
r[k,j];}
превышающими k, только в следующих случ

30.

же  существует путь из вершины в , который проходит чере
ины с номерами не более k-1.
ществует путь из вершины до вершины , проходящий чере
ины с номерами не более k-1, и путь от вершины до
ины , который также проходит через вершины с номерами
олее k-1.
авершению цикла по k определится существование путей м
и парами вершин.
Ахо А., Хопкрофт Д., Ульман Д. (стр. 194-195)
Структуры данных и алгоритмы. : Пер. с англ. : Уч. пос. — М. :
Издательский дом "Вильямс", 2000. — 384 с.
Алгоритм работает «на месте» -- матрица Rk
записывается на месте матрицы R.

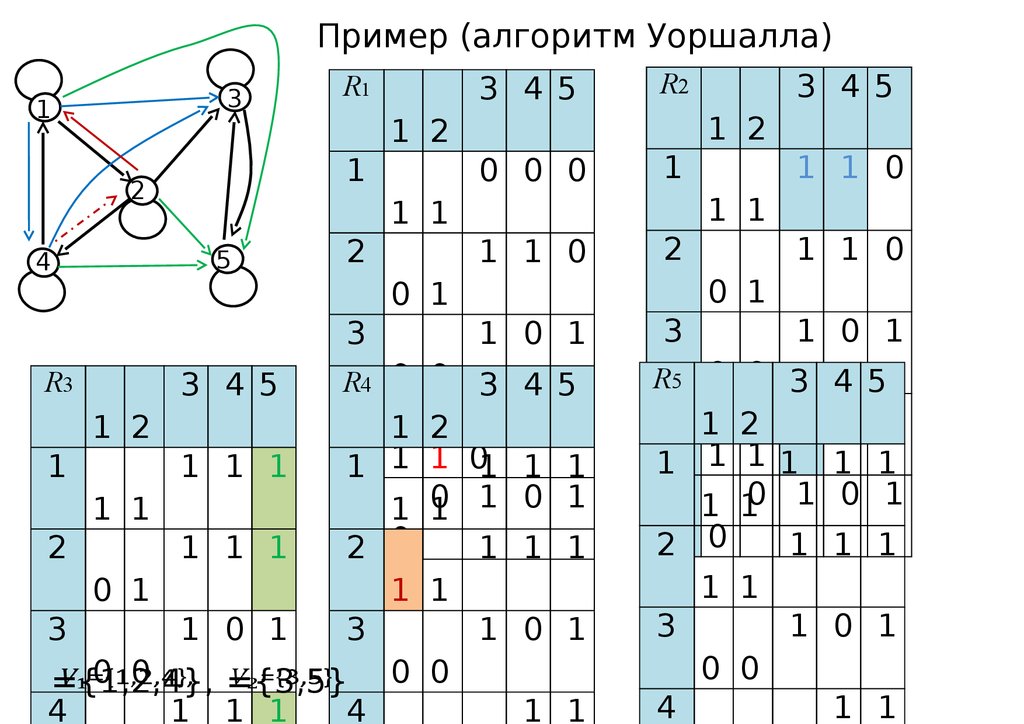
31.

Пример (алгоритм Уоршалла)
3
1
 1
2
4
R1    
5
 2
 3
R3    
 3  4 5 
R4
 4
1 2
 1      1  1  1  1
 5
1 1
 2      1  1  1  2
0 1
 3      1  0  1  3
  0 0
 
={1,2,4},
={3,5}
 4     1   1  1  4
1
 
1
 
0
 
0
 
 1
1
 
 1
0
 
1
 
0
 
2
 
1
 
1
 
0
 
 3  4 5 
R2    
 0  0  0
 1
 1  1  0
 2
 1  0  1
 3
 3  4
 1
0 
 1  1
 1  0
R5
5 
 0
2
1
 
 1
0
 1
1
    1  1  1
1
   1  0  1
0
 
 1  1
 4
 1
 5
 2
1
 
1
 
0
 
 0
1 
 1
1 
 0
1
 3  
0
 4  
2
 
1
 
1
 
 0
2 
 1
10
  
 3  4 5 
 1  1  0
 1  1  0
 1  0  1
 3  4 5 
1   1  0
1  1  1
 1  0  1
 1  1  1
1
   1  0  1
0
 
 1  1

32.

Warshall carried out research and
development in operating systems,
compiler design, language design, and
operations research.
Known for Floyd–Warshall algorithm
https://en.wikipedia.org/wiki/Stephen_Warshall
Warshall Stephen (1935 – 2006)

33.

2.3. Кратчайшие цепи

34.

Волновой алгоритм
 Пусть
задан связный обыкновенный граф.
Поставим задачу найти кратчайшую (с
минимальным числом ребер) цепь, соединяющую
вершины и .
 
Описание алгоритма.
Шаг 1. Помечаем вершину меткой 0.
Шаг 2. Меткой помечаем каждую
вершину, которая еще не помечена и
смежна хотя бы с одной вершиной,
помеченной меткой . Разметка прекращается, как только вершина t
окажется поме-ченной некоторой меткой

35.

Шаг   3. Сама кратчайшая цепь длины отыскивается следующим
образом. Начинаем с вершины t. За берем любую вершину с
меткой и смежную с t, а за – любое ребро, соединяющее
с t. За выбираем любую вершину, помеченную меткой
и смежную с , а за – любое ребро, соединяющее
си так далее, пока не дойдем до вершины

36.

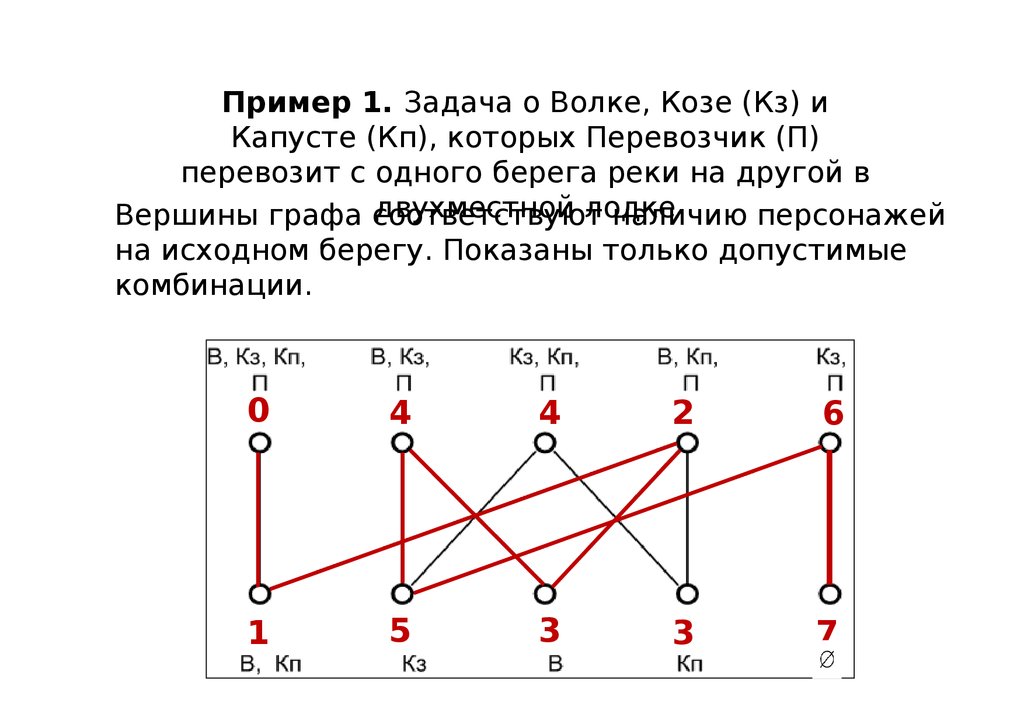
Пример 1. Задача о Волке, Козе (Кз) и
Капусте (Кп), которых Перевозчик (П)
перевозит с одного берега реки на другой в
двухместной лодке
Вершины графа соответствуют
наличию персонажей
на исходном берегу. Показаны только допустимые
комбинации.
0
4
4
2
6
1
5
3
3
7
 

37.

38.

https://www.youtube.com/watch?v=YDX-ohCVtxY

39.

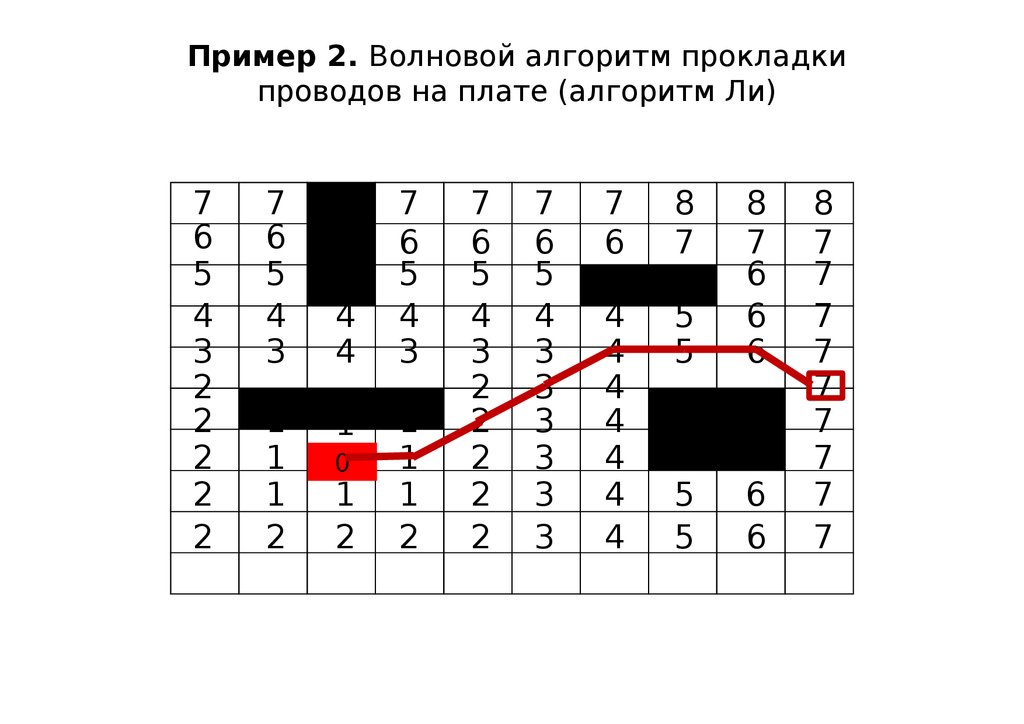
Пример 2. Волновой алгоритм прокладки
проводов на плате (алгоритм Ли)
7
6
5
4
3
2
2
2
2
2
7
6
5
4
3
1
1
1
2
4
4
1
0
1
2
7
6
5
4
3
1
1
1
2
7
6
5
4
3
2
2
2
2
2
7
6
5
4
3
3
3
3
3
3
7
6
8
7
4
4
4
4
4
4
4
5
5
8
7
6
6
6
5
5
5
6
6
6
8
7
7
7
7
7
7
7
7
7

40.

Взвешенный граф
 
Пусть задан граф и отображение ставящее
в соответствие каждому ребру u,
соединяющему пару вершин , число – вес
(длина) ребра. Таким образом задается
матрица длин ребер размерности n × n. Если
ребро отсутствует, то .
Под длиной маршрута понимается сумма
длин ребер, входящих в маршрут.
Требуется найти кратчайший по длине
маршрут. Легко убедиться, что это простая
цепь.

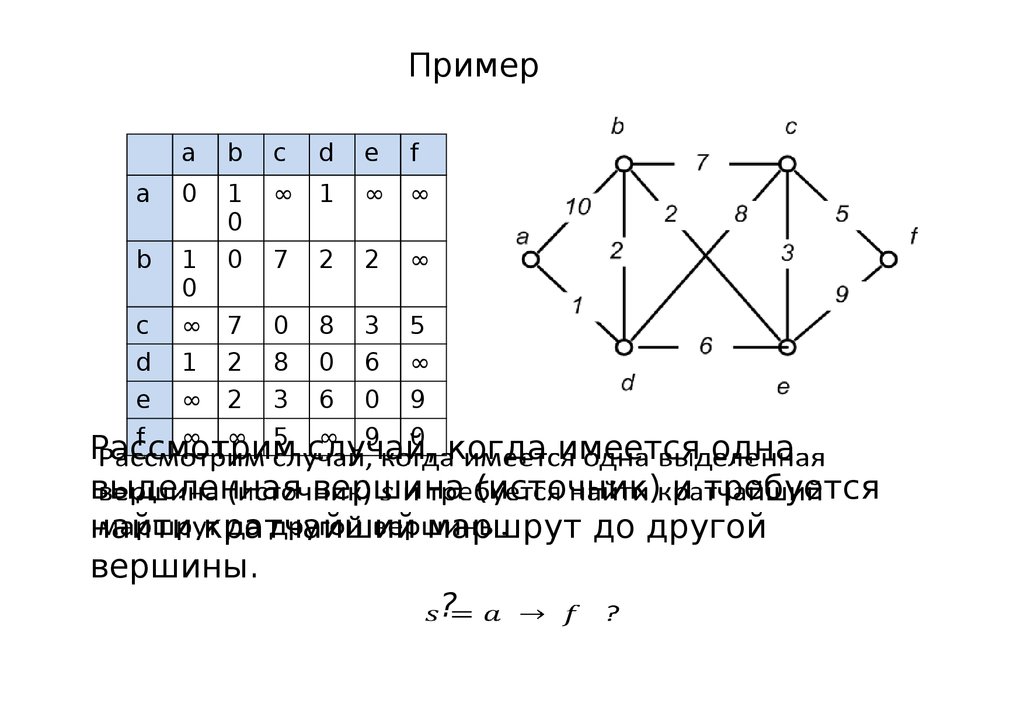
41.

Пример
a
b
c
d
e
f
a
0
1
0
∞
1
∞
∞
b
1
0
0
7
2
2
∞
c
∞
7
0
8
3
5
d
1
2
8
0
6
∞
e
∞
2
3
6
0
9
f
∞
∞
5
∞ 9 0
случай,
когда имеется одна
выделенная вершина (источник) и требуется
найти кратчайший маршрут до другой
вершины.
 ?
 Рассмотрим

42.

Алгоритм Беллмана - Форда
 Алгоритм
заключается в последовательной
разметке вершин графа. Метка при вершине
состоит из двух частей: числовой и
навигационной , которая является ссылкой на
некоторую предшествующую вершину.
 
Шаг 0. Инициализация.
Назначим вершине s числовую метку . Для всех
вершин x, отличных от назначим метки Все
навигационные метки при вершинах ссылаются
на себя:

43.

 
Шаг 1. Итерационный цикл разметки
вершин.
Находим любое ребро для которого
и обновляем числовую метку вершины y на
Очевидно, метка может только уменьшиться:
при Обновленная навигационная метка при
этом ссылается на предшествующую вершину
вызвавшую данное обновление:
Цикл продолжается до тех пор пока метки
не установятся, то есть не найдется больше ни
одной вершины y, для которой можно
уменьшить метку.

44.

 
Шаг 2. Нахождение кратчайшей цепи.
Идем с конца - вершины к началу по
навигационным меткам:
Легко видеть, что при этом разность числовых
меток соседних вершин в точности равна длине
соединяющего их ребра:

45.

 Теорема.
Построенный маршрут
кратчайший и его длина из в есть
Д о к а з а т е л ь с т в о . Пусть в
размеченном с помощью алгоритма графе
имеется произвольный маршрут
длины
 Тогда
+
 

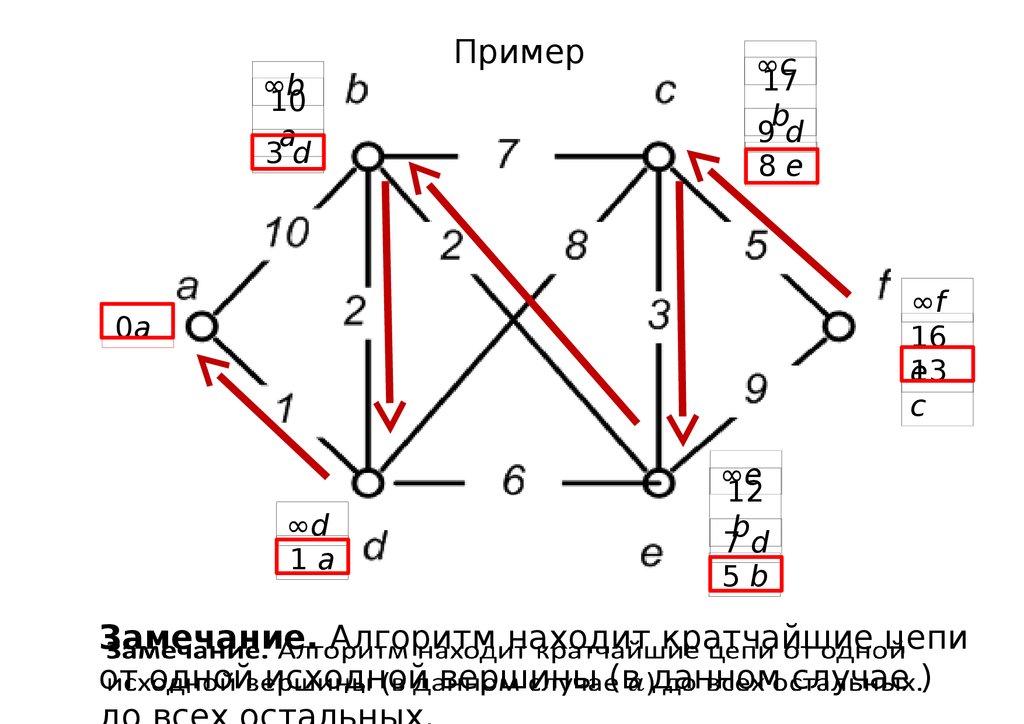
46.

∞b
10
a
3d
Пример
∞c
17
b
9d
8e
∞f
16
13
e
c
0a
∞d
1a
 Замечание.
∞e
12
b
7d
5b
Алгоритм находит кратчайшие цепи
от одной исходной вершины (в данном случае )

47.

Иллюстрация работы алгоритма
Форда
Итераци
и
Ребро
0
1
ab
2
ad
3
bc
4
be
5
db
6
dc
7
de
8
ef
9
eb
a
b
c
d
e
f
0a
∞b
∞c
∞d
∞e
∞f
10a
1a
17b
12
b
3d
9d
7d
16
e
5b
Если метка у вершины не меняется, клетка в
10
ec
8e
следующей строке данного столбца не заполняется.
11
cf
13
Заключительные метки выделены красным
цветом.
c

48.

ком представлении алгоритм Беллмана — Форда более пр
«ручного» исполнения.
ь вершины пронумерованы V={1,2,…,n} и начальная верши
Метка вершины L(x)=[l(x),p(x)], где l(x) – метка расстояния
k
 
 
i
 
 
вершины
x от начальной, p(x) – метка предшествования (навигационная). На шаге ин
ализации i=s=1, l(1)=0, p(1)=1; для осталь
l(x)=
Перебираются тройки i,j,k:
;j
если sum<, то :=sum;
:=min[, ]; p(j):=k
Для нахождения кратчайших цепей/путей между
всеми парами вер-шин нужно выполнить цикл по i.

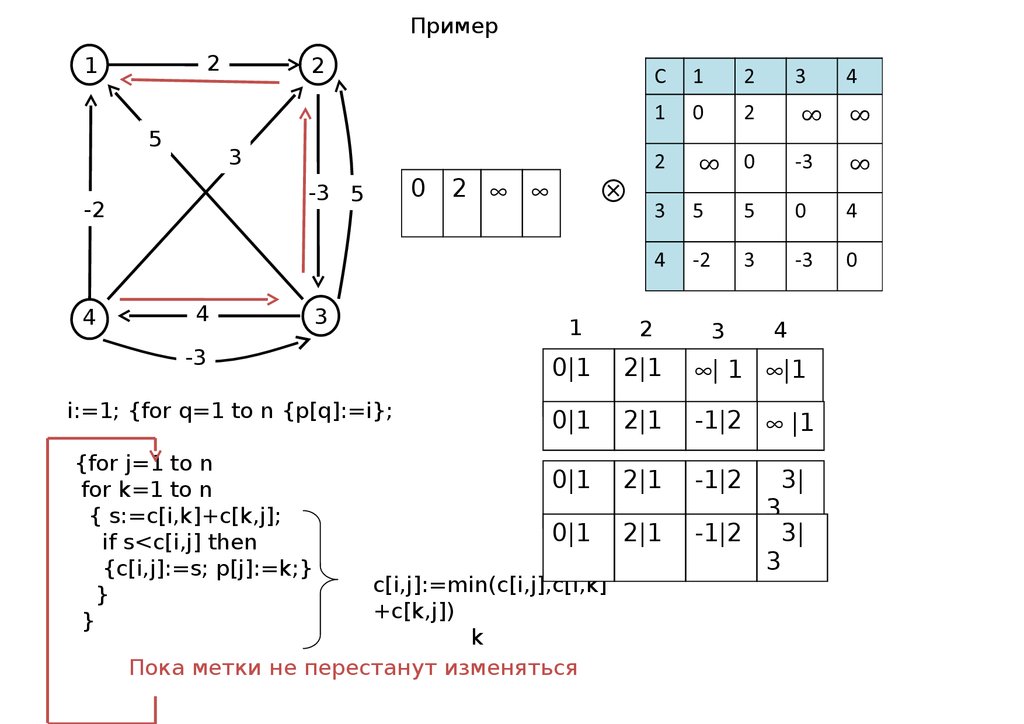
49.

Пример
2
1
5
3
-3 5
-2
4
2
4
3
-3
i:=1; {for q=1 to n {p[q]:=i};
{for j=1 to n
for k=1 to n
{ s:=c[i,k]+c[k,j];
if s<c[i,j] then
{c[i,j]:=s; p[j]:=k;}
}
}
0
2
1
2
0|1
2|1
| 1 |1
0|1
2|1
-1|2 |1
0|1
2|1
-1|2
0|1
2|1
c[i,j]:=min(c[i,j],c[i,k]
+c[k,j])
k
Пока метки не перестанут изменяться
3
4
3|
3
-1|2
3|
3

50.

БЕЛЛМАН, Ричард (1920- 1984) –
«отец «динамического
программирования» американский математик.
Опубликовал 619 статей и 39 книг.
Один из наиболее цитируемых
математиков в мире.
В расцвете творческой жизни
после удаления опухоли на
позвоночнике 11 лет был прикован
к инвалидному креслу, но
ФОРД, Лестер
младший
(1927 сохранил
полную
2017) – американский
математик.
работоспособность
.
Независимо от Беллмана в 1956 г.
предложил алгоритм нахождения
кратчайшего пути в графе, вместе
с Фалкерсоном доказал теорему о
наибольшем потоке в сети.

51.

Алгоритм Дейкстры
 Наиболее
эффективный с точки зрения
трудоемкости алгоритм разметки вершин
 
предложил Дейкстра.
 
Метки вершин
делятся на две категории –
временные
и постоянные
. Временная числовая метка
дает верхнюю границу длины цепи от до этой
вершины. Эти метки постепенно уменьшаются с
помощью итерационной процедуры, и на каждом
шаге итерации одна из временных меток
становится постоянной. Тогда метка уже не
является верхней границей, а дает точную длину
кратчайшей цепи от к вершине с постоянной
меткой.

52.

 Шаг
0. Инициализация.
Назначить вершине s числовую метку и считать
ее постоянной. Вершины с постоянными
метками считаются обработанными и к ним
алгоритм не возвращается.
Для всех назначить метки и считать эти метки
временными.
Текущая вершина
 Шаг
1. Обновление соседних временных
меток из текущей вершины.
Взять текущую вершину Рассмотреть все
смежные с ней вершины с временными
метками и, если то обновить их: .

53.

 
Шаг 2. Превращение метки в постоянную.
а) Найти вершину с наименьшей временной
числовой меткой .
б) Превратить эту метку в постоянную.
в) Считать эту вершину текущей
г) Если есть еще временные метки, возврат на
шаг 1.
д) Если все метки постоянные – переход на шаг
3.
Шаг 3. Построение кратчайшей цепи.
Точно так же, как в алгоритме Беллмана –
Форда – от конца к началу по навигационным
меткам .
При наличии всех постоянных меток

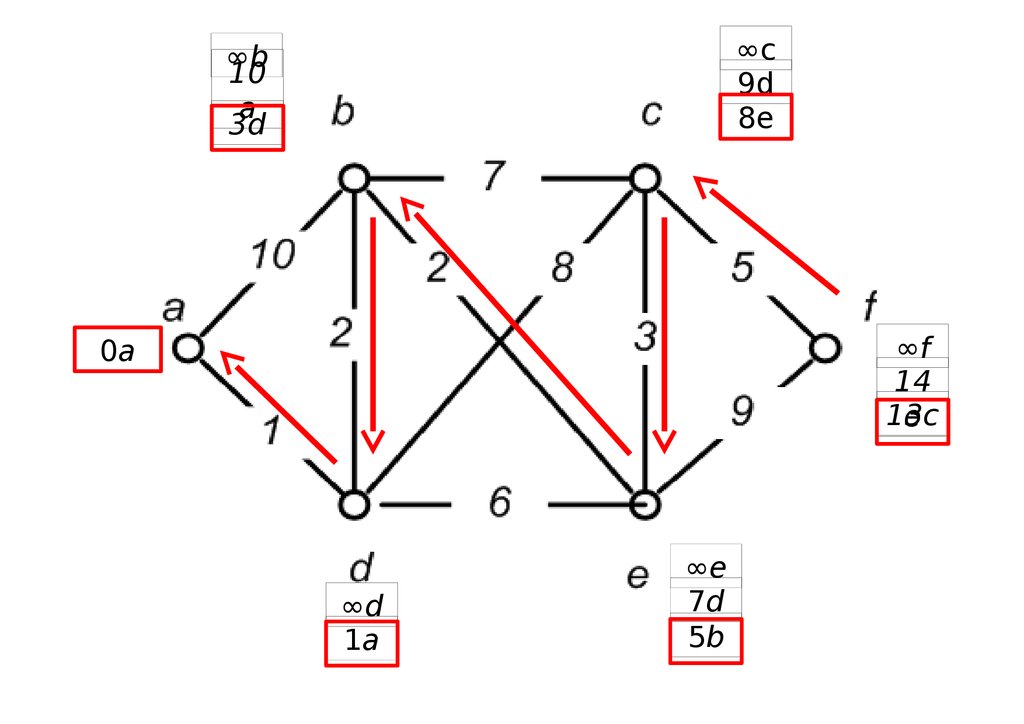
54.

∞c
9d
8e
∞b
10
a
3d
∞f
14
13c
e
0a
∞d
1a
∞e
7d
5b

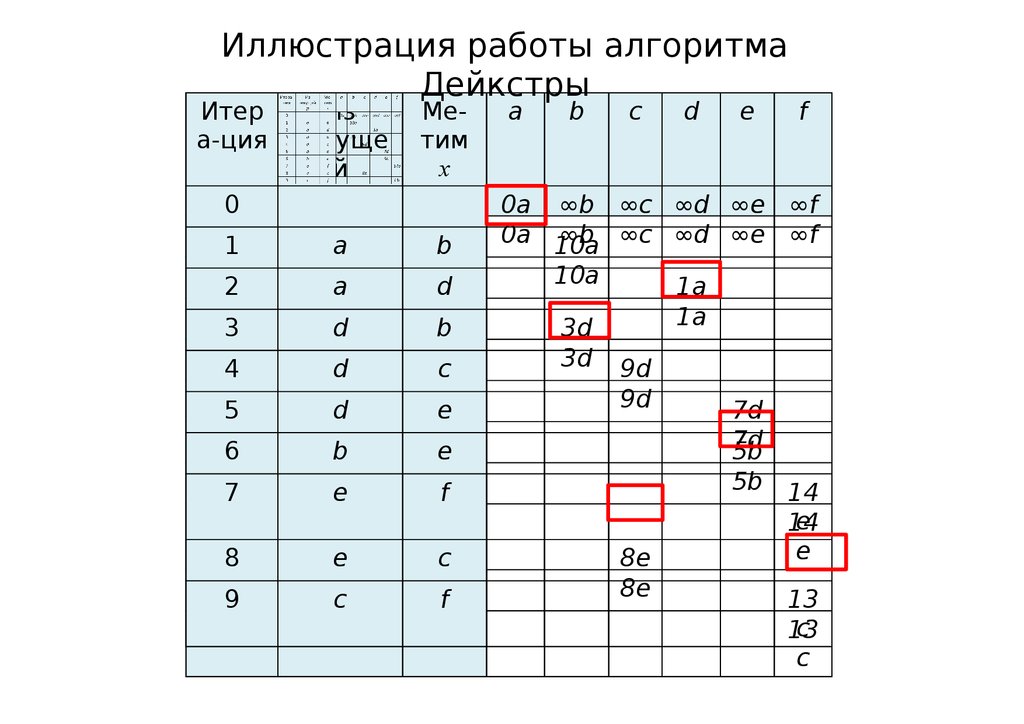
55.

Иллюстрация работы алгоритма
Дейкстры
Итер
а-ция
0
0
1
Из
текуще
й
Метим
x
a
a
a
b
b
d
a
d
d
d
d
b
b
c
d
d
d
b
c
e
e
e
7
8
8
9
b
e
e
e
e
c
ef
f
c
cf
9
c
f
1
2
2
3
3
4
4
5
5
6
6
7
a
b
c
d
e
f
0a ∞b ∞c ∞d ∞e ∞f
0a 10a
∞b ∞c ∞d ∞e ∞f
10a
1a
1a
3d
3d
9d
9d
7d
7d
5b
5b
8e
8e
14
e
14
e
13
c
13
c

56.

Обобщения
1. Алгоритмы Беллмана – Форда и Дейкстры легко
распространяются на случай ориентированных
(частично ориентированных) графов, при этом
каждое неориентированное ребро
представляется двумя дугами, ориентированными
в разные стороны. Более того, веса (длины) этих
дуг могут быть различными.
2. В алгоритме Беллмана – Форда допускаются
отрицательные веса ребер, такие постановки
задачи иногда полезны в приложениях. Этим он
принципиально отличается от алгоритма
Дейкстры, где отрицательные веса невозможны.
Но «всеядность» алгоритма Беллмана – Форда
оплачивается его более высокой трудоемкостью.

57.

ДЕЙКСТРА, Эдсгер
(Edsger Dijkstra; 19302002). Нидерландский
учёный, труды которого
оказали большое влияние
на развитие информатики;
один из авторов языка
Алгол и концепции
структурного
программирова-ния. По
образованию физиктеоретик. Во второй
половине 1950-х годов в
поисках путей
оптимизации
разводки печатных плат

58.

Алгоритм Флойда
 Предыдущие
алгоритмы (Беллмана – Форда
и Дейкстры) давали возможность находить
кратчайшие маршруты между одной
начальной вершиной (источником ) и или
всеми другими вершинами графа.
Алгоритм Флойда (Флойда – Уоршалла),
разрабо-танный в 1962 г., позволяет найти
длины кратчайших маршрутов между всеми
парами вершинами.
Замечание. В алгоритме Флойда, так же как и в
алгоритме Беллмана – Форда, нет ограничений на
неотрицательность длин ребер, как будет показано
в примере.

59.

 Пусть
задан взвешенный униграф (ориентированный,
неориентированный, смешанный) G=(V,E) с матрицей весов (длин)
С= ,
где =0; =ребра (, );
навигационная матрица (матрица предшествований) P
Инициализация
и -- матрицы, полученные for
на i=1
k – йtoитерации.
n
 
  :=C;
for j=1 to n
p[i,j]:=i;
Основной цикл
Алгоритм работает «на месте»: старые значения
элементов матриц
C и P заменяются на новые; по завершению цикла по k
(k=n)
C становится матрицей длин кратчайших цепей/путей, а P

60.

 
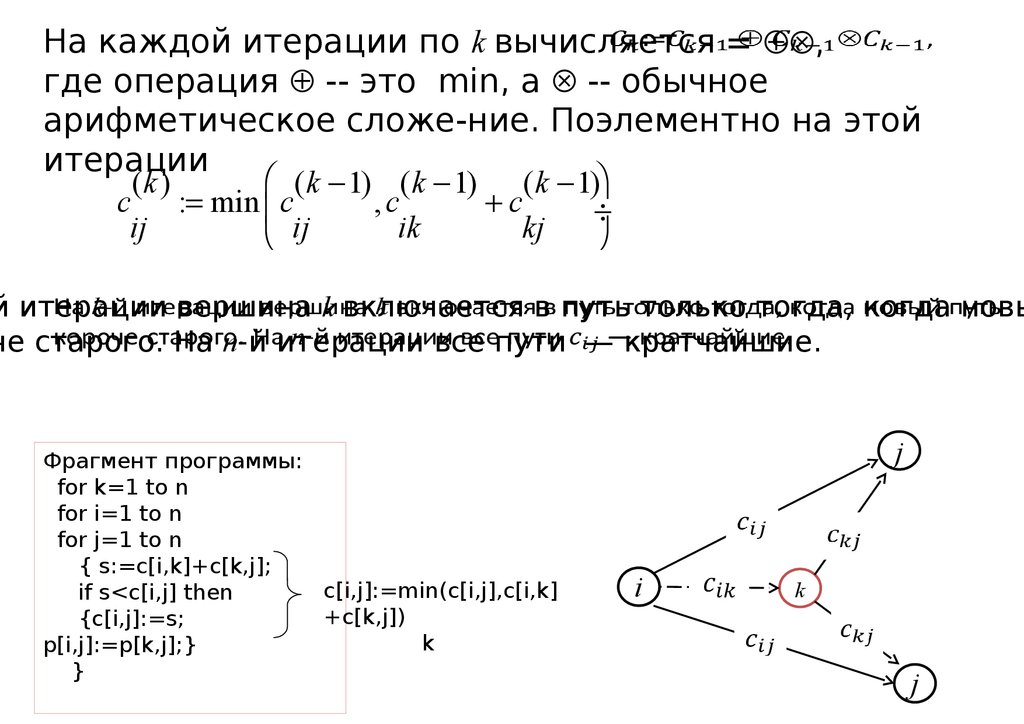
На каждой итерации по k вычисляется
= ,
где операция -- это min, а -- обычное
арифметическое сложе-ние. Поэлементно на этой
итерации
(k 1) (k 1) (k 1)
(k )
c : min c
,c
c
ij
ij
ik
kj
 
й итерации
вершина k включается в путь только тогда, когда новы
че старого. На n-й итерации все пути — кратчайшие.
Фрагмент программы:
for k=1 to n
for i=1 to n
for j=1 to n
{ s:=c[i,k]+c[k,j];
c[i,j]:=min(c[i,j],c[i,k]
if s<c[i,j] then
+c[k,j])
{c[i,j]:=s;
k
p[i,j]:=p[k,j];}
}
j
 
i
 
 
k
 
 
j

61.

-2
1
3
2
5
-3
4
2
5
4
3
-3
-2
1
3
2
5
-3
2
4
5
4
3
-3
C0    
 3  4
1 2
 1   -  3 0 2
3
 2
   2
0
 3
 0 3
 4  
 0
     3  4
4 5 5 
1 2
 1   -  3 0 2
3
 2
   2
0
 3
 0 3
P0    
 3 4 
1 2
 1      1 1
1 1
 2     2  2
2 2
 3      3 3
3 3
 4   4  4  4
P1      3 4 
4  
1 2
 1      1 1
1 1
 2     2  2
2 2
 3      3 3
3 3

62.

-2
1
3
2
2
-3
2
4
5
4
3
-3
1
 3
-2
0
2
2
-3
4
2
4
4
 
1
 1  
0
 2
 4  
 
4
1
 1  
0
 2
3
-3
 3
   3  4
2
-  0 2
3
   2
0
 0 3
 0
   3  4
2 4 
2
-  0 2
3
   2
0
 0 3
P2    
1
 1  
1
 2  
2
 3  
3
 4 P 3
4
2
 
1
 
2
 
3
 1
1 
 1  
1
 2  
2
 3  
3
 3 4 
 2 1
2  2
 3 3
 44 
  2 3
2
   2 1
1
  2  3
2
   3 3
3

63.

-2
1
0
-3
2
2
-1
2
4
4
4
3
-3
1
-2
3
2
5
-3
2
4
5
4
3
-3
 
1
 1  
0
 2
P4      3 4 
   3  4
2
1 2
-  0  1      2 1
2
3
1 1
   2
 2     2  3
0
4 2
 3
-  0  3      3 3
 Найдем,
например, кратчайший путь из
1
3
4 1
2 в 1 по
 4  
 0
 4   1 на
 2исходном
 4
меткам
предшествования
графе
4 2 4 
4  
(в обратном порядке). Выберем строку 2
в матри-це P4. Вершине 1 предшествует
4,
4-й – вершина
    3,
 3 3-й
4  – вершина 2: 1-43-2.
 2 1
  2
  2  3
Сам путь: 2-3-4-1 длины =3.
4 2

64.

Замечание. Алгоритмы Беллмана – Форда и Флойда
работают корректно, если в графе нет циклов отрицательной длины
(сумма длин
которых отрицательна). В противном случае длина
кратчайшей цепи/
пути уменьшается до - (программа зацикливает). Это
обнаруживается,
 
Этотнекоторые
алгоритмдиагональные
применим и элементы
для нахождения
когда
становятся
цепи/пути наибольшей длины (критического пути).
отрицательными.
Операция заменяется на max, и в матрице весов
=ребра (, ).
Другой пример: найти цепь/путь максимальной
надежности в сети связи. Надежность ребра — это
вероятностная характеристика 0 1; надежность
цепи определяется
как произведение (обычное) надежностей ребер
цепи.

65.

ФЛОЙД, Роберт В  (Robert W
Floyd, 1936 – 2001) —
американский учёный в области
теории вычислительных систем.
Лауреат премии Тьюринга. Роберт
окончил школу в возрасте 14 лет,
перепрыгнув три класса. Флойд
не имел титула PhD.
В Стэнфорде Флойд тесно
работал с Дональдом Кнутом, в
том числе в качестве главного
редактора серии его знаменитых
книг «Искусство
программирования».