Похожие презентации:
Оценка надёжности систем централизованного теплоснабжения
1. Оценка надёжности систем централизованного теплоснабжения (СЦТ)
Вопросы лекции:Расчёт показателей безотказности
Расчёт коэффициента готовности
Методы обеспечения безотказной
работы и прогноз надёжности ТС
Определение закона надёжности на основе
статистических данных об отказах
http://www.ribalco.exponenta.ru
2. Нормативные значения показателей надёжности СЦТ согласно СНиП 41- 02-2003
Вероятность безотказной работы- источника тепла - рит = 0,97;
- тепловых сетей - ртс = 0,90;
- абонента раб = 0,99;
Для системы централизованного
теплоснабжения: рсцт = рит · ртс
· раб =
= 0,97 · 0,90 · 0,99 = 0,86.
Коэффициент готовности системы
Кг = 0,97
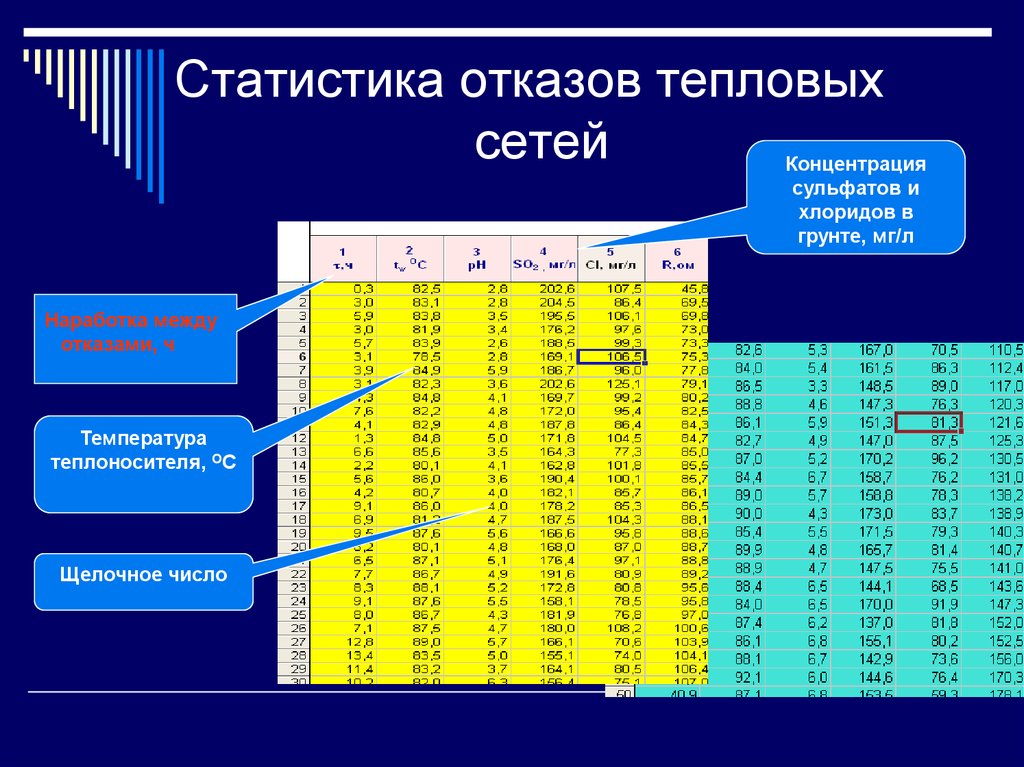
3. Статистика отказов тепловых сетей Санкт-Петербурга
Влияние срока службына повреждаемость
тепловых
сетей
Статистика отказов
тепловых
ГУП
«ТЭК СПб»
сетей
Санкт-Петербурга
Срок службы
Доля
от
Повреждаемость,
Показатель
1996
г общего
2001
г
2003 г
50 %
тепловых
сетей
тепловых сетей,
Общая длина
лет
количества, %
требует
5083 замены.
5134
Ежегодный
19 прирост
Среднегодовое кол-во
7247,5
тепловых
сетей
с
дефектов, шт.
10- 15
30 сроком
истекшим
Удельная
1,4 - 1,51
повреждаемость, службы составляет
отк./км.
15 – 25
27 170 км
примерно
Удельная
трубопроводов, км
0 - 10
повреждаемость за
отопительный сезон,
Более 25
шт./ км
0,27
0,37
24
отк./км
5263
0,77
1,63
1,52
2,11
0,35
~ 10
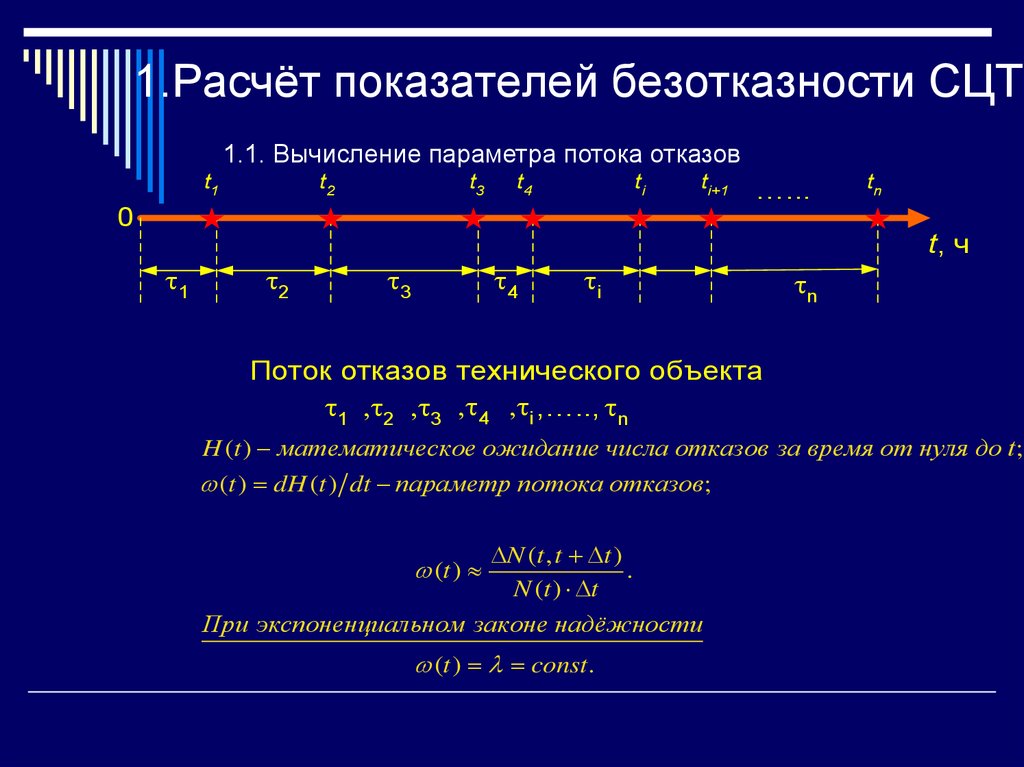
4. 1.Расчёт показателей безотказности СЦТ
1.1. Вычисление параметра потока отказовt1
t2
t3
t4
ti
ti+1
…...
0
tn
t, ч
1
2
3
4
i
n
Поток отказов технического объекта
1 2 3 4 i ,….., n
H (t ) математическое ожидание числа отказов за время от нуля до t ;
(t ) dH (t ) dt параметр потока отказов;
N (t , t t )
.
N (t ) t
При экспоненциальном законе надёжности
(t )
(t ) const.
5. 1.2. Расчёт показателей безотказности по методике ВНИПИЭНЕРГОПРОМ
p (t ) exp( t ), гдеamK c d 0,28 параметр потока отказов;
a, m параметры, характеризующие
отказы системы;
d диаметр трубопровода, м;
K c 3 И 2,6 коэффициент старения
системы;
И
n
индекс утраты ресурса;
n0
n срок службы участка трассы;
n0 нормативный срок службы.
6. 1.2.1.Пример расчёта безотказности ТС по методике ВНИПИЭНЕРГОПРОМ
Исходная информация:Коэффициент a = 0,00003;
Коэффициент старения трубопровода Kc =1;
Коэффициент m = 0,5;
Вычислить: вероятность безотказной работы магистрали диаметром
500 мм при сроке эксплуатации t =1000 ч.
Решение:
1. Параметр потока отказов amK c d 0,28 0, 00003 0,5 1, 0 0,50,28 0, 0000124;
2. Вероятность безотказной работы p(t ) exp( t ) 0,998;
Ответ: Вероятность безотказной работы магистрали диаметром 500 мм
при наработке 1000 ч равна p(1000) = 0,998.
7. 1.3. Расчёт вероятности безотказной работы по методике СНиП 41- 02-2003
p (t ) exp( L t ), гдеПример
Исходная информация:
n = 7032 ед;
L = 5134 км;
Т = 8760 ч;
Вычислить: вероятность безотказной
определённого диаметра , зафиксированное
работы участка трубопровода длиной
10 км при его наработке 1000 ч.
за назначенное время T на определённой длине
n
параметр потока отказов , 1 (км ч );
T
n количество отказов трубопровода
трассы, ед / км;
Т назначенное время контроля надёжности
обычно 8760 ч;
L длина трассы, для которой вычисляется
вероятность безотказной работы, км.
Решение
1. Параметр потока отказов
n
1,56 10 4 ,1 ( км ч);
L T
2. Вероятность безотказной работы
p (t ) exp( 1,56 10 4 1000) 0,855;
Ответ: Вероятность безотказной работы трубопровода длиной 10 км
при его наработке 1000 ч равна p = 0,855.
8. 1.4. Нестандартные показатели безотказности тепловых сетей
1.4.1. «Параметр потока отказов»w = Σ Мот· от/ Σ М·
где Мот - материальная характеристика участков тепловой
сети, выключенных из работы при отказе , м2;
от - время вынужденного выключения участков сети,
вызванное отказом и его устранением, ч;
Σ М · - произведение материальной характеристики
тепловой сети данной системы теплоснабжения на
плановую длительность ее работы за определённый
период времени (обычно за год),м2·ч;
М = d·L - материальная характеристика, м2.
9. 1.4.2. Относительный аварийный «недоотпуск» тепла
q = ΣQав / ΣQ ,где:
ΣQав - аварийный «недоотпуск» тепла за год, Гкал;
ΣQ - расчетный отпуск тепла системой теплоснабжения за год, Гкал.
10.
1.4.3. Коэффициент надёжности СЦТК над
к з кв к т кб к р к с
6
, где
кз = 0,2 – 1,0 – коэффициент учёта уровня резервирования системы;
кв = 0,3 – 1,0 – коэффициент соответствия мощности источника и
пропускной способности сети;
кт = 0,6 – 1.0 – коэффициент учёта наличия у источника тепла резервного
топливоснабжения ;
кб = 0,6 – 08 – коэффициент учёта наличия у источника тепла резервного
водоснабжения;
кр = 0,6 – 0,8 – коэффициент учёта наличия у источника тепла резервного
электропитания;
кс = 0,5 – 1,0 – коэффициент учёта старения сетей;
11. 2. Расчёт коэффициента готовности СЦТ
8760 z1 z2 z3 z4, где
8760
z1 время неготовности СЦТ при
Kг
нерасчётных значениях температуры
атмосферного воздуха , ч;
z2 время неготовности источника тепла , ч;
z3 время неготовности тепловых сетей , ч;
z4 время неготовности абонента, ч;
При нормативном значении
z год z1 z2 z3 z4 264 ч.
Кг 0, 97
12. 3. Методы обеспечения безотказной работы и прогноз надёжности СЦТ
3.1. Расчёт потребного количества ЗИП3.2. Прогнозирование безотказности системы при малой
начальной наработке
3.3. Прогнозирование надёжности системы после очередного
отказа
3.4. Прогнозирование работоспособного состояния системы
при фиксированном времени восстановления
3.5. Прогнозирование безотказности на основе моделей
множественной регрессии
3.6. Расчёт и корректировка сроков технического обслуживания
ТС
13. 3.1. Расчёт потребного количества ЗИП
Основные понятия и определенияЗапасная часть (элемент) – составляющая часть механизма, предназначенная для замены аналогичных частей в работающем механизме
Одиночный комплект запасных частей – определённое количество
элементов и сборочных единиц, предназначенных для поддержания
работоспособности объекта между плановыми ремонтами
Ремонтный комплект запасных частей – элементы (детали) и сборочные
единицы для, необходимые для проведения планового ремонта
ГОСТ 15.601-98. Межгосударственный стандарт. Система разработки
и постановки продукции на производство. Техническое
обслуживание и ремонт техники. Основные положения.
ОКСТУ 0028. Дата введения 1999-07-01.
14. 3.1.1. Пример расчёта потребного количества запасных элементов
Исходная информация:Параметры закона надёжности Тср = 1000 ч;
s = 200 ч;
Планируемая наработка системы: t = 8 000 ч;
Рассчитать: Необходимое количество запасных элементов для
обеспечения безотказной работы системы в течение заданного
времени с вероятностью 0,99.
Решение
t
s 2 t 8000
200 2 8000
n
q( p)
2,33
10,
3
Tcp
1000
10003
Tcp
где q ( p ) q (0,99) 2,33 квантиль стандартной нормальной
функции распределения при уровне значимости 0, 01.
Ответ: Для обеспечения безотказной работы системы с вероятностью 0,99
в течение 8 000 ч необходимо 10 запасных элементов.
15. 3.2. Прогнозирование безотказности системы при малой начальной наработке
Оценка вероятности того, что при наработкесистемы в течение времени X отказов не будет
0
t, ч
X
p0 (t ) F (t ), где
F (t ) функция надёжности системы;
Пример
Исходная информация : Параметры закона надёжности
Тср 1 000 ч; s 300 ч;
Планируемая наработка системы t 200 ч.
Вычислить : Вероятность отсутствия отказов при заданной наработке.
Решение
F (t ) 1 F (t ) 1 pnorm(t , Тср, s ) 1 pnorm(200,1000,300) 0,996.
Примечание. Функция
pnorm( ) это стандартная функция вычисления
функции нормального распределения в пакете Mathcad .
Ответ: При наработке системы в течение 200 ч с вероятностью 0,996
отказов не будет.
16. 3.2.1. Прогнозирование отказа системы при малой начальной наработке
Оценка вероятности того, что при наработке системы втечение времени X произойдёт отказ
0
p1 (t ) F (t ), где
t, ч
X
F (t ) функция ненадёжности системы;
Пример
Исходная информация : Параметры закона надёжности
Тср 1 000 ч; s 300 ч;
Планируемая наработка системы t 200 ч.
Вычислить : Вероятность появления хотя бы одного отказа при заданной наработке.
Решение
F (t ) pnorm(t , Тср, s ) pnorm(200,1000,300) 0, 0038.
Ответ: При работе системы в течение 200 ч вероятность возникновения хотя
бы одного отказа равна 0,0038.
17. 3.3.Прогнозирование надёжности системы после очередного отказа
Оценка вероятности того, что после очередного отказа системаt
t
t
t
t
t
проработает ещё x ч
1
p( x)
2
3
4
i
i+1
0
1
F (u )du , где
Тср x
x
F (t ) функция надёжности системы;
Пример
Исходная информация : Параметры закона надёжности
Тср 1 000 ч; s 300 ч;
Планируемая наработка системы x 200 ч.
Вычислить : Вероятность того, что после очередного отказа система
проработает безотказно ещё 200 ч.
Решение
1
1
p( x)
F
(
u
)
du
1 pnorm(u,1000,300) du 0,80.
Тср x
1 000 200
Ответ: Вероятность того, что после очередного отказа система проработает
безотказно ещё 200 ч равна 0,80.
t, ч
18. 3.4. Прогнозирование работоспособного состояния системы при фиксированном времени восстановления
Tvt1
Tv
t2
0
Tv
t3
Tv
ti
Tv
ti+1
t, ч
x
pt ( x)
1
F (u )du,
Tcp Tv x
где Tcp средняя наработка между отказами;
Tv среднее время восстановления после отказа;
F (u ) функция надёжности системы;
Пример
Tcp 1000 ч; s 350 ч; Tv 10 ч.
Закон надёжности нормальный
Вычислить : вероятность застать систему в работоспособном состочнии
при наработке 100 ч.
Решение
1
1
pt ( x)
F
(
u
)
du
1 pnorm(u,1000,350) du 0,892.
Tcp Tv x
1000 10 100
Ответ: В момент наработки системы 100 ч она будет с вероятностью 0,892
в работоспособном состоянии.
19. 3.5. Прогнозирование безотказности на основе моделей множественной регрессии
Факторы, определяющие коррозионную стойкость тепловых сетейматериал труб, тепло- гидроизоляционных и
защитных покрытий;
коррозионная активность грунта;
уровень и химический состав грунтовых вод;
водо- и воздухопроницаемость грунта;
температура теплоносителя;
воздействие внутренних и внешних растягивающих
усилий и вибрация;
состояние дренажа;
наличие блуждающих токов;
наличие и работоспособность катодной защиты;
20. Статистика отказов тепловых сетей
Концентрациясульфатов и
хлоридов в
грунте, мг/л
Наработка между
отказами, ч
Температура
теплоносителя, ОС
Щелочное число
21. Влияние различных факторов на наработку между отказами тепловых сетей
-241,5996+3,5455*x+1,8521*y-0,0049*x*x-0,0286*x*y+0,0042*y*y= =631,3808-14,4107*x-27,8817*y+0,089*x*x+0,0515*x*y+3,0697*y*y
= 304,9347-1,7461*x-2,5022*y-0,0002*x*x+0,0175*x*y-0,0044*y*y
b0 b1 qSO b2 qCl b3 pH b4 R.
2
Уравнение множественной линейной регрессии,
100
60
80
устанавливающее связь между наработкой между50
отказами
60
4040
40
3020
тепловой сети и эксплуатационными факторами
20
200
0
10-20
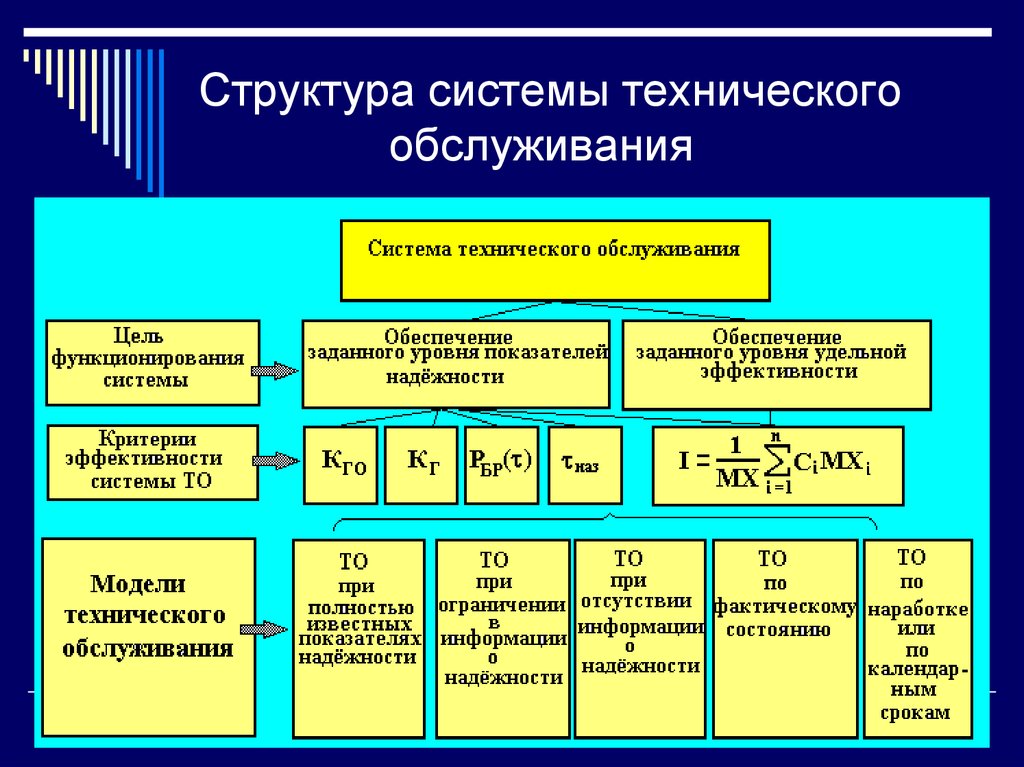
22. 3.6. Расчёт и корректировка сроков технического обслуживания ТС
Основные понятия и определенияТехническое обслуживание – комплекс
организационных и технических мероприятий по
обеспечению работоспособного состояния
технического объекта
ГОСТ 15.601- 98. Межгосударственный стандарт. Система разработки и постановки
продукции на производство. Техническое обслуживание и ремонт техники.
Основные положения. ОКСТУ 0028. Дата введения 1999-07-01.
ГОСТ 19489- 80 Система технического обслуживания и ремонта техники.
Испытания на ремонтопригодность. Основные положения.
Постановление Госстандарта России от 27.06.80 N 3147
23. Структура системы технического обслуживания
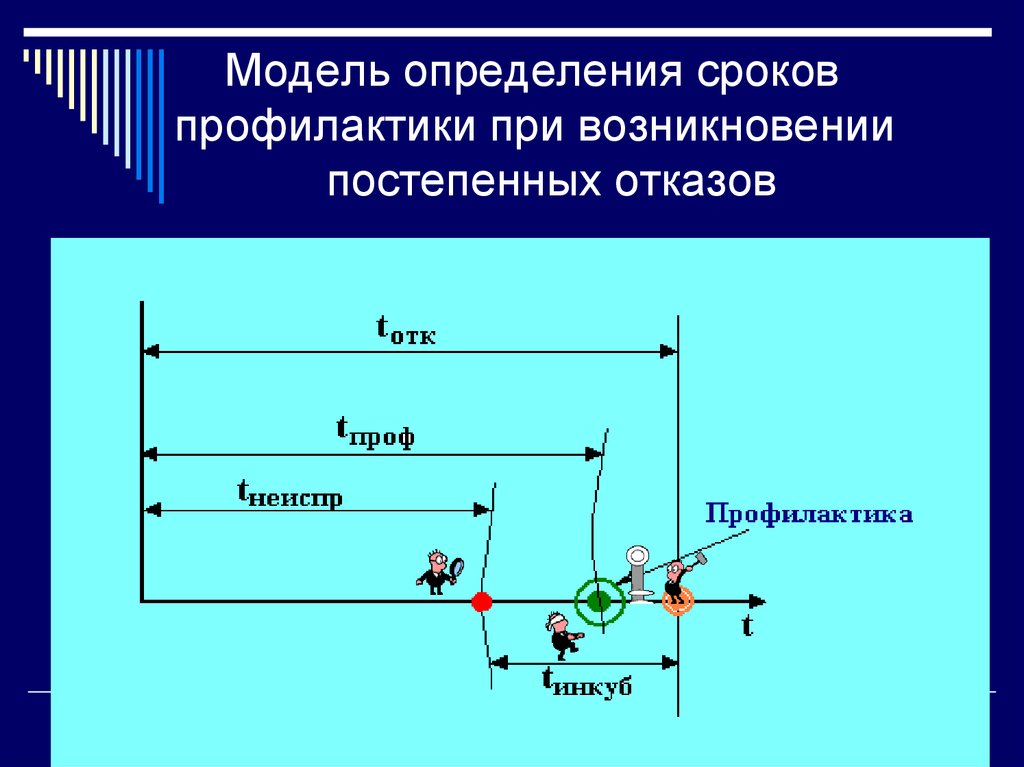
24. Модель определения сроков профилактики при возникновении постепенных отказов
25. 3.6.1. Пример расчёта сроков технического обслуживания (постепенные отказы)
Исходная информация:1 – интенсивность возникновения неисправности, 1/ч;
2 – интенсивность проявления отказа, 1/ч;
t ТО– время очередного технического обслуживания, ч;
Решение
Пример
1 = 0,001 , 1/ч;
2 = 0,1 , 1/ч;
tTO
ln 2 ln 1
;
2 1
tTO
ln 0,1 ln 0, 001
46 ч.
0,1 0, 001
Ответ: Отказ объекта можно предотвратить в случае, если
проводить техническое обслуживание через каждые 46 ч.
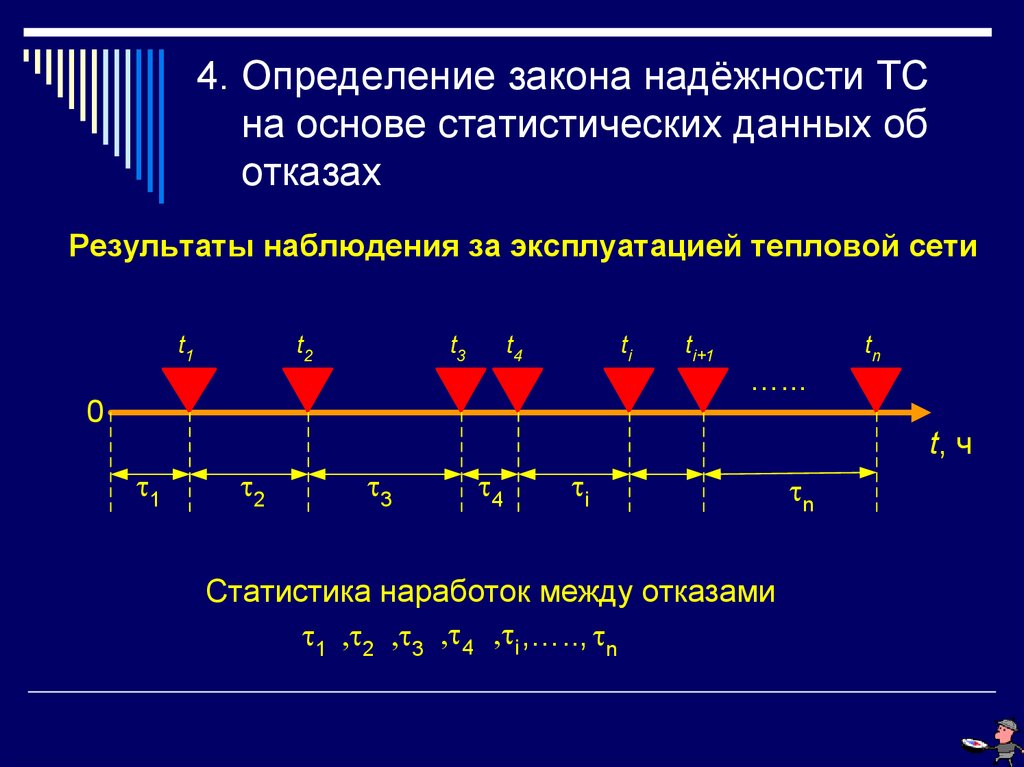
26. 4. Определение закона надёжности ТС на основе статистических данных об отказах
Результаты наблюдения за эксплуатацией тепловой сетиti
t4
t3
t2
t1
ti+1
…...
0
tn
t, ч
1
2
3
4
i
Статистика наработок между отказами
1 2 3 4 i ,….., n
n
27. 4.1.Определение закона надёжности и оценка параметров по случайно цензурированным выборкам
Случайно цензурированная выборка – это статистиканаработок объекта до отказа и до прекращения наблюдения,
сформированная в произвольный (случайный) момент
времени и объединённая в общий вариационный ряд.
Различают:
- выборку цензурированную слева;
- выборку цензурированную справа;
- выборку со смешанным цензурированием.
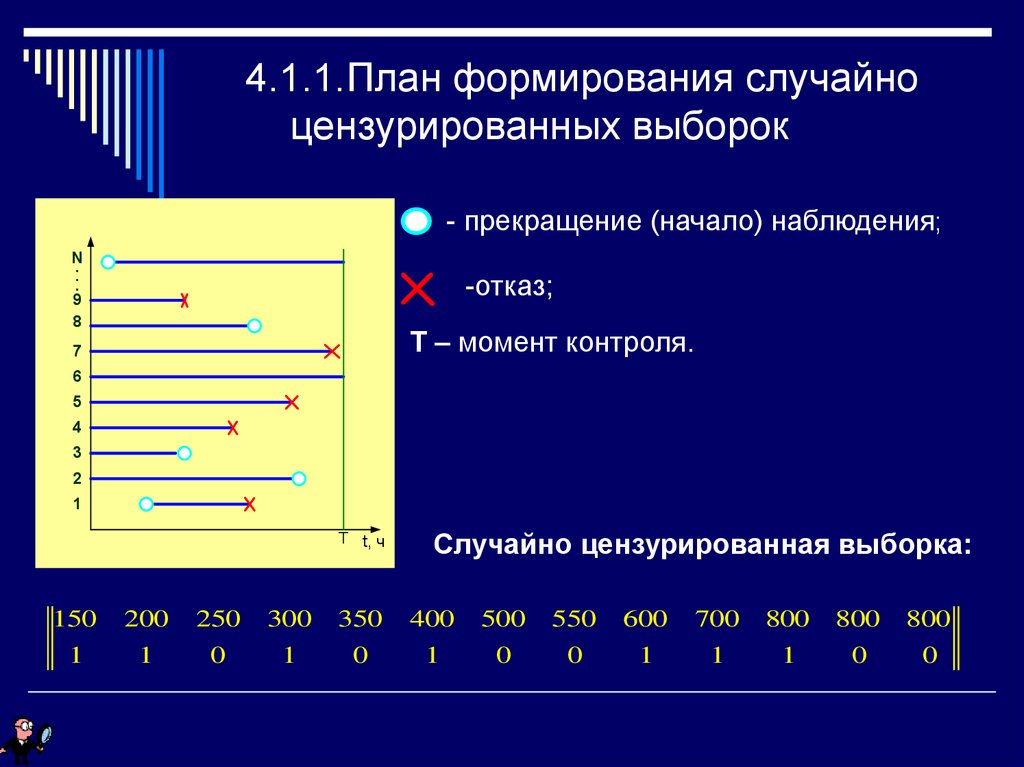
28. 4.1.1.План формирования случайно цензурированных выборок
- прекращение (начало) наблюдения;N
..
.
-отказ;
9
8
Т – момент контроля.
7
6
5
4
3
2
1
Т t, ч
Случайно цензурированная выборка:
150
200
250
300
350
400
500
550
600
700
800
800
800
1
1
0
1
0
1
0
0
1
1
1
0
0
29. 4.1.2. Пример определения закона надёжности и оценки его параметров для случайно цензурированных выборок
1. Формирование матрицы случайно цензурированнойвыборки
450 470 540 580 592 601 603 651 752 900
1
0
1
1
0
1
0
1
1
1
,
где первая строка матрицы наработки объекта;
вторая строка матрицы индикаторный массив;
1 соответствует наработке до отказа;
0 соответствует наработке до приостановки наблюдения;
30. Заключение
Статистический анализ наработок до отказа позволяетопределить закон надёжности объекта и его основные
параметры.
При известном законе надёжности можно решать
следующие задачи:
- проверять соответствие показателей надёжности
требованиям НТД;
- разрабатывать мероприятия по обеспечению
нормативных показателей надёжности в эксплуатации;
- прогнозировать работоспособность объекта;
- планировать сроки и объёмы ТО;
- рассчитывать потребные комплекты ЗИП.
























 Промышленность
Промышленность








