Logika rozmyta

1.

Logika rozmyta
Została rozwinięta przez Lotfi A. Zadeh w latach 60
ubiegłego wieku w celu zapewnienia matematycznych
zasad i funkcji które były by podobne do ludzkiego
języka

2.

Logika rozmyta
Logika rozmyta wprowadza obliczoną wartość średnią
między absolutną prawdą i absolutnym fałszem z
rezultatem spomiędzy zakresu 0,0 i 1,0. Wprowadza
ona odcienie szarości między czarny/biały i
prawdę/fałsz.

3.

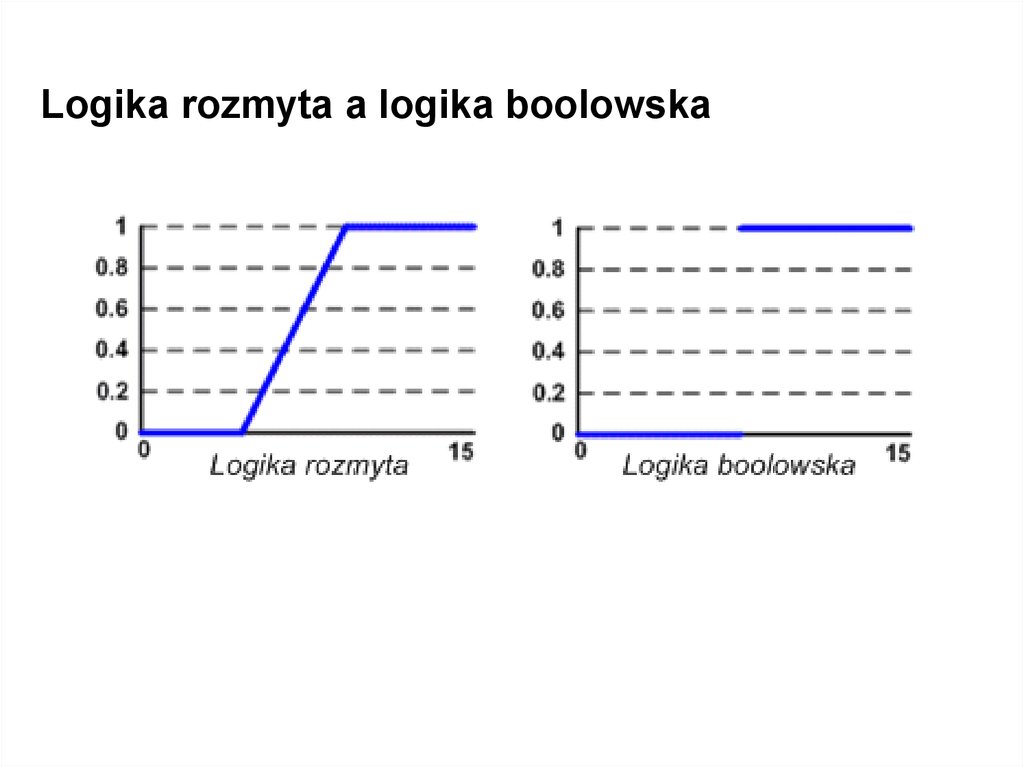
Logika rozmyta a logika boolowska

4.

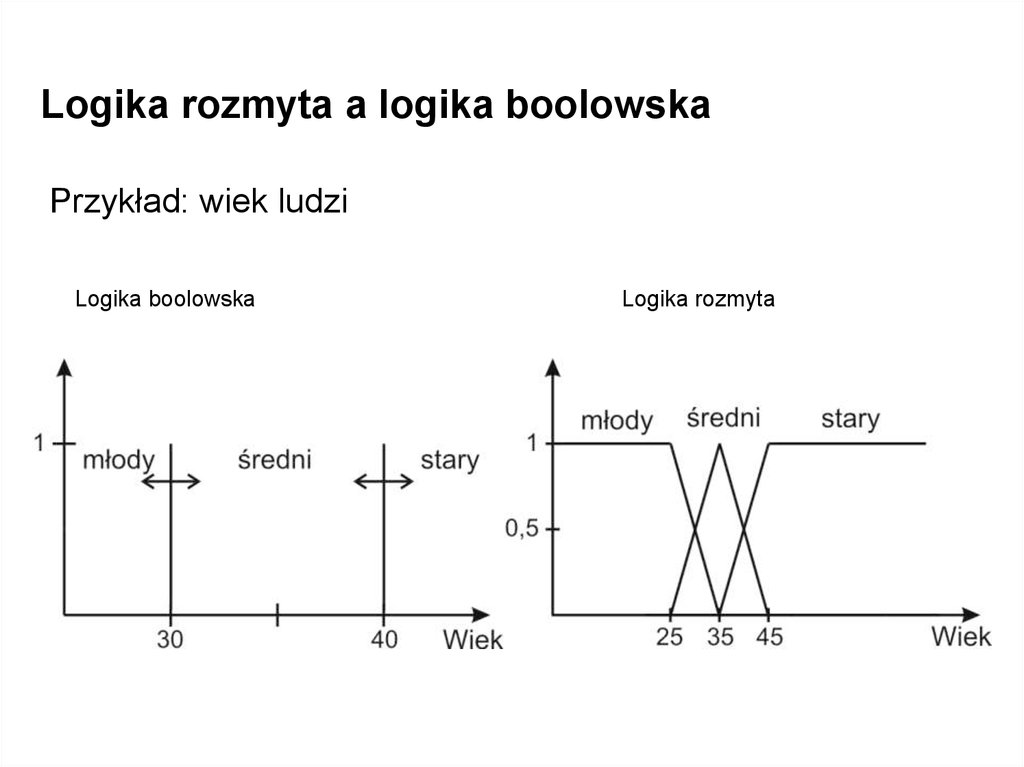
Logika rozmyta a logika boolowska
Przykład: wiek ludzi
Logika boolowska
Logika rozmyta

5.

Zmienna lingwistyczna
Zmienna lingwistyczna jest czwórką (N;T;X;MN), gdzie
• N nazwa zmiennej np. wiek
• T zbiór wartości lingwistycznych np. {młody, średni, stary}
• X przestrzeń rozważań np. [0; 125] lat
• MN funkcja semantyczna MN : T zbiór funkcji przynależności

6.

Zbiory rozmyte
1. Należy ustalić obszar rozważań X nazywany
przestrzenią – zakres zmian rozważanych wielkości
Zbiorem rozmytym A w pewnej (niepustej) przestrzeni X
nazywamy zbiór par:
A {( x, A ( x); x X )
w którym
A : X [0,1]
jest funkcją przynależności zbioru rozmytego A.

7.

Zbiory rozmyte – zapis symboliczny
A
A ( x1 )
x1
A ( xn )
xn
n
A ( xi )
i 1
xi
Elementami zbioru X mogą być nie tylko liczby, ale
również inne przedmioty, osoby lub pojęcia. Zapis ten ma
charakter symboliczny. Kreska ułamkowa nie oznacza
dzielenia a przyporządkowanie poszczególnym
elementom zbioru stopni przynależności. Podobnie znak
„+” nie oznacza dodawania, a sumę mnogościową
elementów.

8.

Zbiory rozmyte
Funkcja przynależności każdemu elementowi x przypisuje
jego stopień przynależności do zbioru rozmytego A, przy
czym można wyróżnić 3 przypadki:
A ( x) 1
oznacza pełną przynależność elementu x do
zbioru rozmytego A
A ( x) 0
oznacza brak przynależności elementu x do
zbioru rozmytego A
0 A ( x) 1 oznacza częściową przynależność elementu
x do zbioru rozmytego A

9.

Zbiory rozmyte - przykład
Niech naszym zbiorem X będą osoby, a zbiorem rozmytym A
osoby wysokie.
Funkcja przynależności:
0
A ( x) ( x 170) / 20
1
gdy wzrost < 170 cm
gdy 170 cm< wzrost < 190 cm
gdy wzrost > 190 cm

10.

Zbiory rozmyte - przykład
Funkcja przynależności:

11.

Zbiory rozmyte - przykład
Zbiór A:
Osoba x
Darek
Kamil
Zbyszek
Sławek
Karol
Mariusz
Jacek
Wzrost
Stopień przynależności
do A
193
139
128
182
175
179
187
1
0
0
0,6
0,25
0,45
0,85

12.

Zbiory rozmyte - przykład
Zbiór A:
A={(Darek,1);(Kamil,0);(Zbyszek,0);(Sławek,0.6);(Karol;0.25);(
Mariusz,0.45);(Jacek,0.85)}
1
0
0
0,6
0,25
0,45
0,85
A
Darek Kamil Zbyszek Slawek Karol Mariusz Jacek

13.

Zbiory rozmyte - definicje
Wysokość zbioru rozmytego A oznaczamy przez h(A) i
określamy jako:
h( A) sup A ( x)
x X
W przypadku zbiorów przeliczalnych jest to maximum funkcji
przynależności.
Przykład:
Jeżeli X={1,2,3,4,5} oraz
0,2 0,4 0,7
A
1
2
4
to h(A)=0,7

14.

Zbiory rozmyte - definicje
Normalnym nazywamy zbiór rozmyty wtedy i tylko wtedy, gdy
h(A) = 1. Jeśli zbiór rozmyty A nie jest normalny, to możemy go
znormalizować poprzez przekształcenie:
( x)
Azn ( x) A
h( A)
gdzie h(A) jest wysokością tego zbioru.
Przykład:
Zbiór rozmyty:
A
0,1 0,5 0,3
2
4
6
Po znormalizowaniu przybiera postać:
Azn
0,2 1 0,6
2 4 6

15.

Zbiory rozmyte - definicje
Zbiór rozmyty A jest równy zbiorowi rozmytemu B, co
zapisujemy A = B, wtedy i tylko wtedy, gdy: A(x) = B(x) dla
każdego x X.

16.

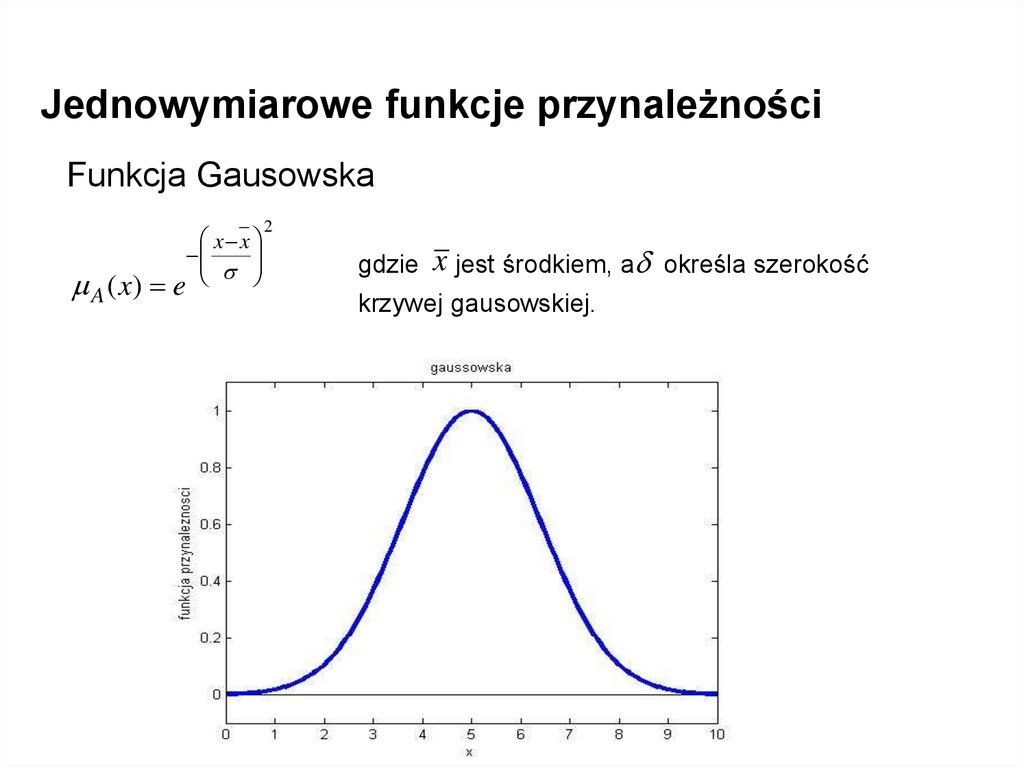
Jednowymiarowe funkcje przynależności
Funkcja Gausowska
A ( x)
x x
e
2
gdzie
x jest środkiem, a określa szerokość
krzywej gausowskiej.

17.

Jednowymiarowe funkcje przynależności
Funkcja przynależności typu dzwonowego
( x , a , b, c )
1
x c
1
a
2b
gdzie parametry a, b, c określają wygląd funkcji. a
określa szerokość, b nachylenie, c środek

18.

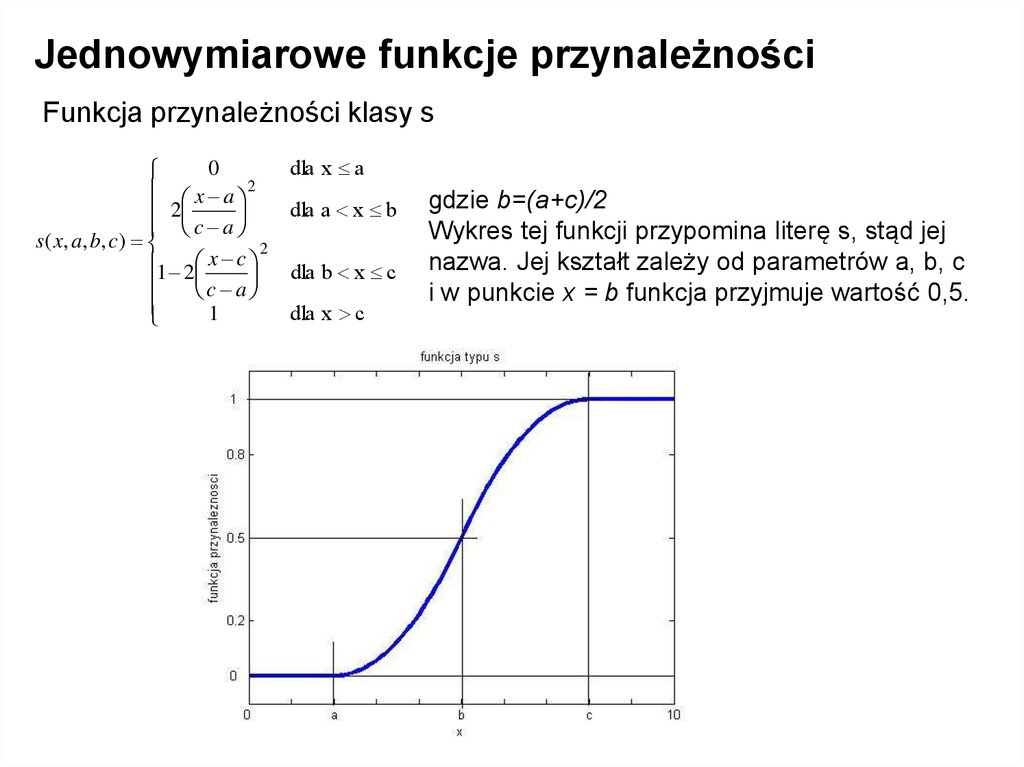
Jednowymiarowe funkcje przynależności
Funkcja przynależności klasy s
0
x a 2
2
c a
s ( x, a, b, c)
2
1 2 x c
c a
1
dla x a
dla a x b
dla b x c
dla x c
gdzie b=(a+c)/2
Wykres tej funkcji przypomina literę s, stąd jej
nazwa. Jej kształt zależy od parametrów a, b, c
i w punkcie x = b funkcja przyjmuje wartość 0,5.

19.

Jednowymiarowe funkcje przynależności
Funkcja przynależności klasy
Tą funkcję przynależności definiuje się poprzez funkcję klasy s:
b
s
(
x
,
c
b
,
c
, c)
dla x c
2
( x, b, c)
b
1 s( x, c, c , c b) dla x c
2
Funkcja ta przyjmuje wartości zerowe
dla x c+b oraz x c – b, natomiast w
punktach x = c b/2 jej wartość wynosi
0,5

20.

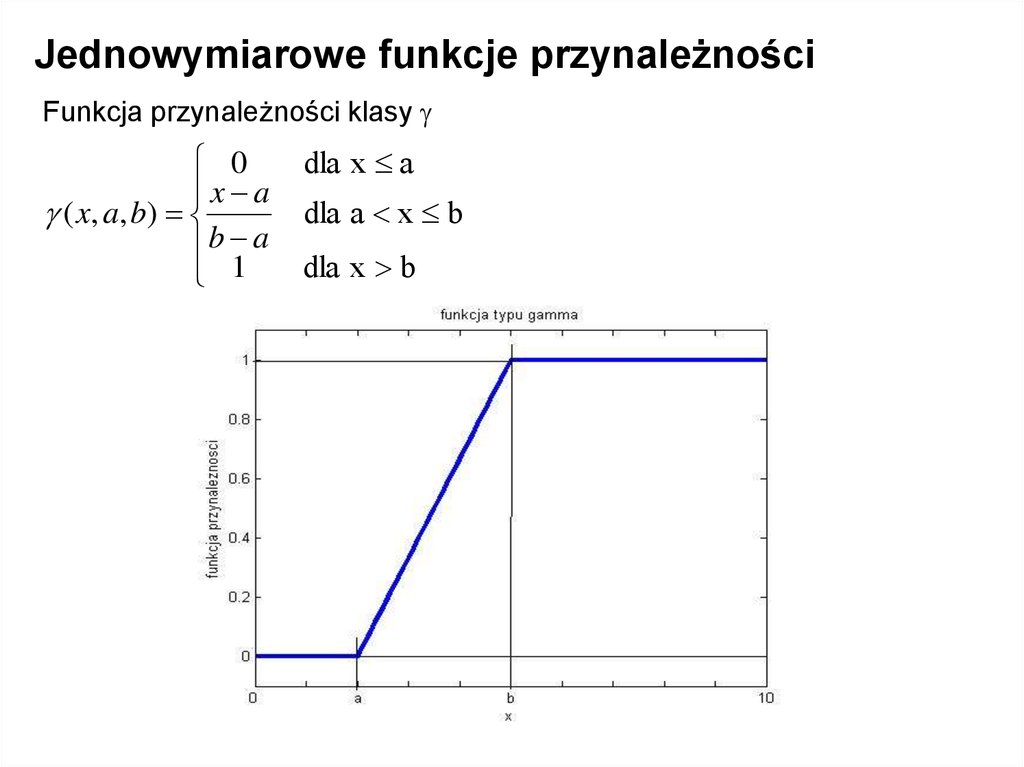
Jednowymiarowe funkcje przynależności
Funkcja przynależności klasy
0
x a
( x, a , b )
b a
1
dla x a
dla a x b
dla x b

21.

Jednowymiarowe funkcje przynależności
Funkcja przynależności klasy t
0
x a
b a
t ( x , a , b, c ) c x
c b
0
dla x a
dla a x b
dla b x c
dla x c

22.

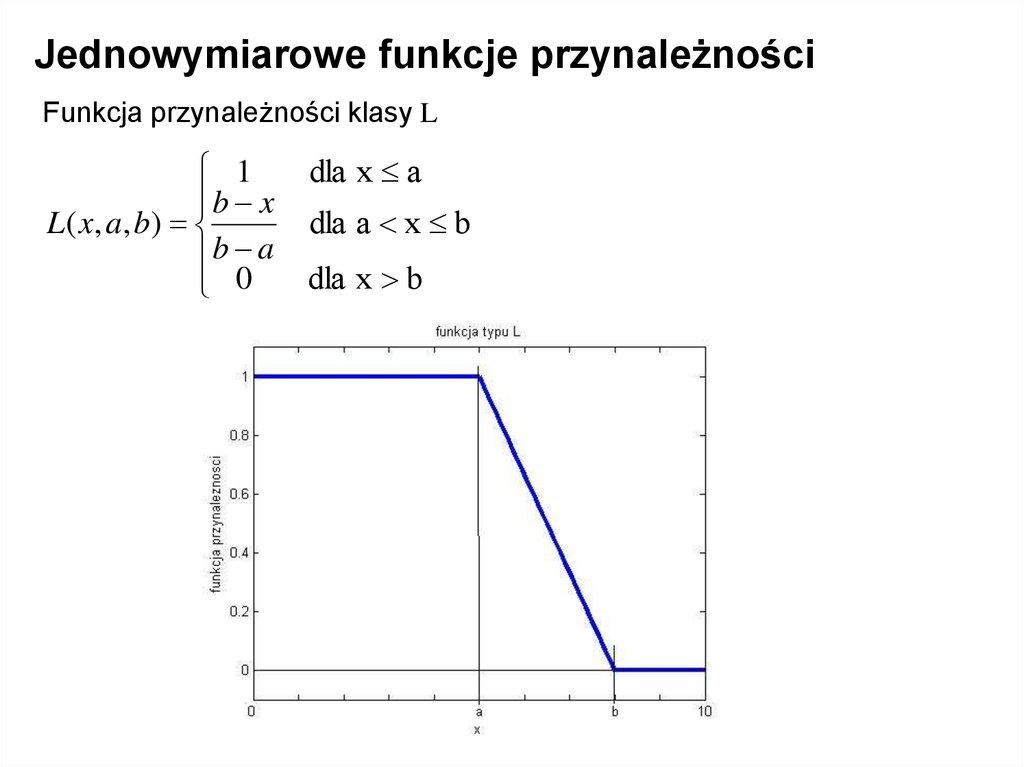
Jednowymiarowe funkcje przynależności
Funkcja przynależności klasy L
1
b x
L ( x, a , b )
b a
0
dla x a
dla a x b
dla x b

23.

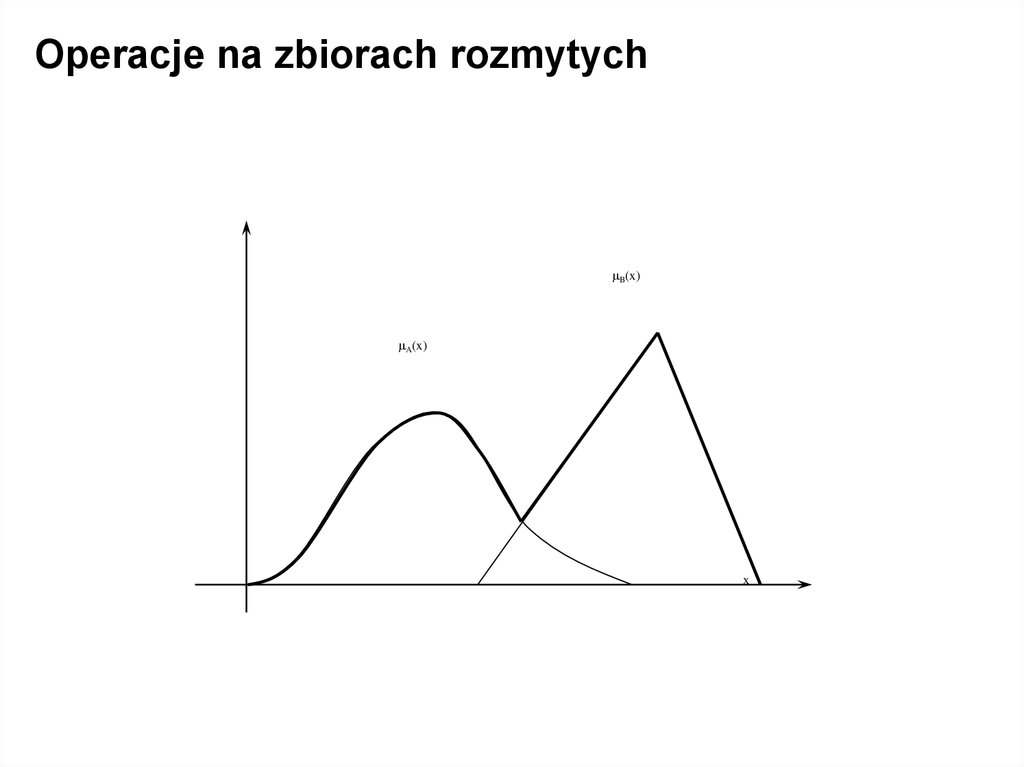
Operacje na zbiorach rozmytych
Sumą zbiorów rozmytych A i B jest zbiór rozmyty A B
określony funkcją przynależności:
A B(x) = max( A(x), B(x)) dla każdego x X.
Suma większej ilości zbiorów A1, A2, A3, …, An określona jest
podobną funkcją przynależności:
A1 A2 A3… An (x) = max( A1(x), A2(x) , A3(x), …, An(x)) dla
każdego x X.

24.

Operacje na zbiorach rozmytych
B(x)
A(x)
x

25.

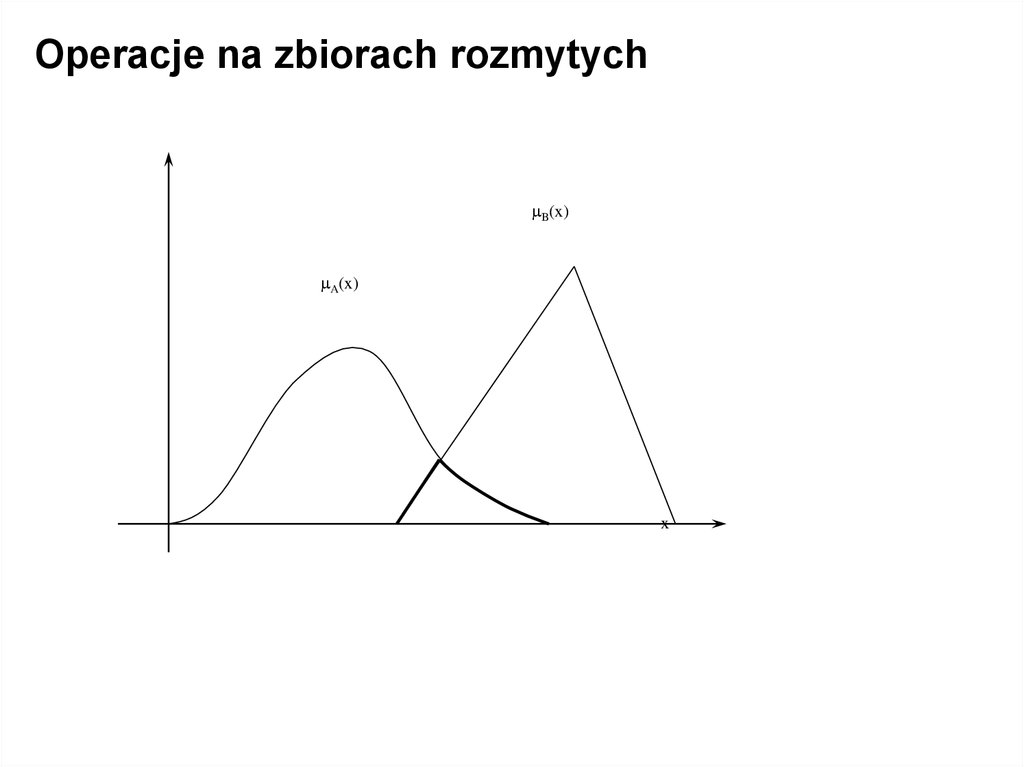
Operacje na zbiorach rozmytych
Przecięciem zbiorów rozmytych A, B X jest zbiór rozmyty
A B o funkcji przynależności:
A B(x) = min( A(x), B(x))
dla każdego x X.
Przecięcie większej ilości zbiorów A1, A2, A3, …, An określone
jest podobną funkcją przynależności:
A1 A2 A3… An (x) = min( A1(x), A2(x) , A3(x), …, An(x))
dla każdego x X.

26.

Operacje na zbiorach rozmytych
B(x)
A(x)
x

27.

Operacje na zbiorach rozmytych
Dopełnieniem zbioru rozmytego A X jest zbiór rozmyty A’
o funkcji przynależności:
A’(x) = 1- A(x)
dla każdego x X.