Dynamika bryły sztywnej

1. Slajd 1

Dynamika bryły
sztywnej
1

2. Slajd 2

Bryła sztywna
Układ cząstek w którym odległości między cząstkami
nie zmieniają się w czasie.
ri
rij
rj
Jeżeli położenie cząstek opisujemy
r
za pomocą wektorów ri i j , to
wektor
rij ri r j
łączący obie cząstki musi być
wektorem stałym

3. Slajd 3

Położenie bryły sztywnej
w przestrzeni
• Położenie 1-go punktu (np. środka
masy) i dwóch dodatkowych punktów.
• Bryła sztywna ma sześć stopni
swobody jej położenie w przestrzeni
opisują 3 współrzędne i 3 kąty.

4. Slajd 4

Ruch bryły sztywnej
Bryła sztywna może poruszać
się ruchem postępowym.
Wtedy wektory prędkości są
takie same dla wszystkich
punktów – bryła porusza się
jak „punkt materialny”.

5. Slajd 5

Ruch bryły sztywnej
Może też poruszać się ruchem
obrotowym. Wtedy wszystkie
punkty ciała poruszają się po
okręgach.
Najczęściej jednak występuje superpozycja ruchu
postępowego i obrotowego.
vi v0 ri
v0 – prędkość punktu przez który przechodzi oś obrotu

6. Slajd 6

Położenie, prędkość, przyspieszenie
jako wielkości kątowe
Długość
2 r
s
prędkość kątowa:
(t ) d (t )
lim
t 0
t
dt
Kąt
2
Położenie kątowe:
s
co daje:
r
przyspieszenie kątowe:
(t ) d (t )
lim
t 0
t
dt
Przesunięcie kątowe, prędkość i przyspieszenie kątowe mogą być:
• dodatnie, kiedy obrót zachodzi przeciwnie do kierunku wskazówek zegara
• ujemne, kiedy obrót zachodzi zgodnie z kierunkiem wskazówek zegara

7. Slajd 7

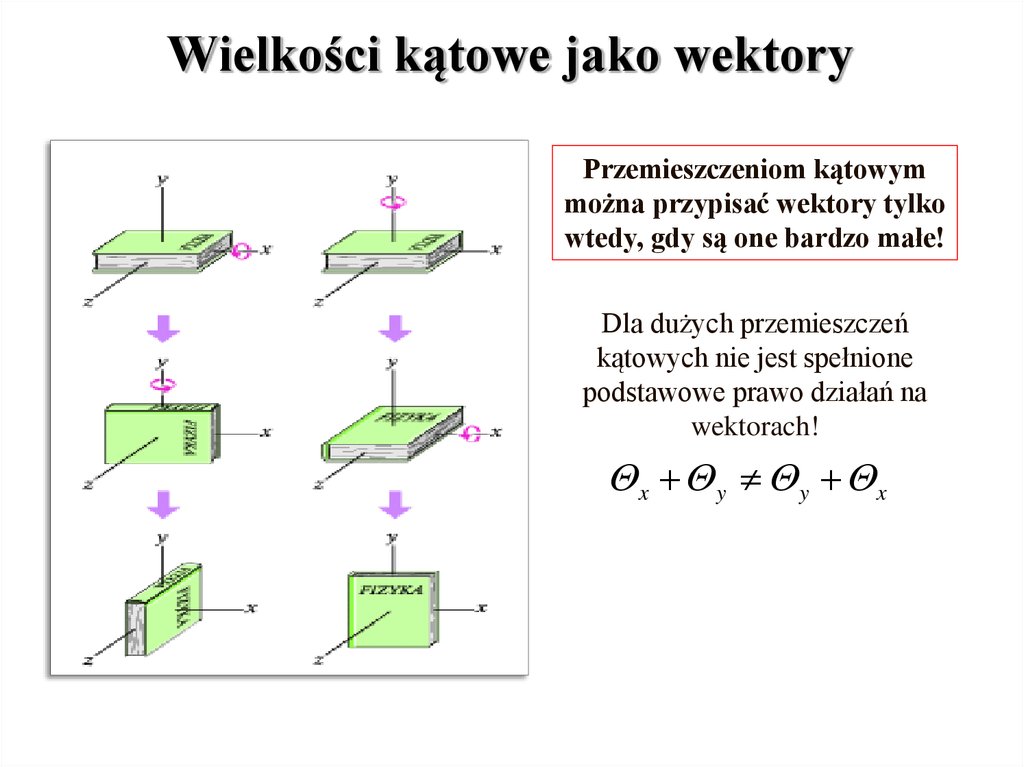
Wielkości kątowe jako wektory
Czy przemieszczenie kątowe, prędkość i przyspieszenie
kątowe mogą być opisane za pomocą wektorów?

8. Slajd 8

Wielkości kątowe jako wektory
Przemieszczeniom kątowym
można przypisać wektory tylko
wtedy, gdy są one bardzo małe!
Dla dużych przemieszczeń
kątowych nie jest spełnione
podstawowe prawo działań na
wektorach!
x y y x

9. Slajd 9

Całkowita energia kinetyczna bryły
sztywnej
1
Ek mi vi2
i 2
2
1
m
v
i 2 i 0 ri
1
1
1
2
mi v02 mi ri mi 2 v 0 ri
i 2
i 2
i 2
1
2 1
2
2 2
mi v0 mi ri sin ( , ri ) v 0 mi ri
2 i
2 i
i
energia kinetyczna ruchu
postępowego bryły
energia kinetyczna ruchu
obrotowego bryły
energia mieszana
(znika dla środka
masy w punkcie 0)

10. Slajd 10

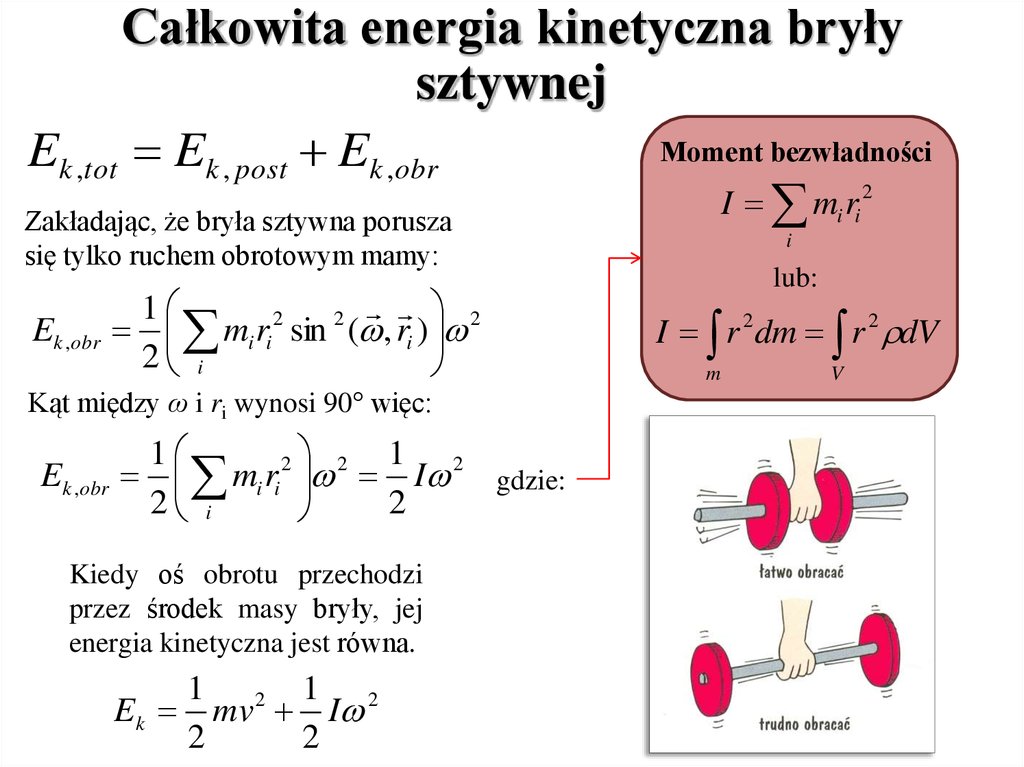
Całkowita energia kinetyczna bryły
sztywnej
Moment bezwładności
Ek ,tot Ek , post Ek ,obr
I m r
Zakładając, że bryła sztywna porusza
2
i i
i
się tylko ruchem obrotowym mamy:
Ek ,obr
1
2
2 2
mi ri sin ( , ri )
2 i
Kąt między ω i ri wynosi 90° więc:
Ek ,obr
1
1 2
2 2
mi ri I gdzie:
2 i
2
Kiedy oś obrotu przechodzi
przez środek masy bryły, jej
energia kinetyczna jest równa.
1 2 1 2
Ek mv I
2
2
lub:
I r 2 dm r 2 dV
m
V

11. Slajd 11

Przykład: Moment bezwładności
jednorodnego koła
I r 2 dm r 2 dV
m
r
Długość łuku:
s r
ds rd
Objętość elementarna:
dV rd dr h
Gęstość materiału:
M
2
R h
R
dr
d
0
V
2
M
r 2 rd dr h
R h
2
0
2
M
3
2 r d dr
R 0 0
R
M R4 1
2 2
MR 2
R 4 2
1
I MR 2
2

12. Slajd 12

Przykład: Moment bezwładności
jednorodnego pręta
Obrót wokół końca:
3 L
L
M
M x
Iy x
dx
L
L 3
0
2
y
dx
x
0
1
ML2
3
Obrót wokół środka masy:
L
3 L/2
L/2
I sm
M
M x
x
dx
L
L 3
L / 2
2
L / 2
1
ML2
12

13. Slajd 13

Twierdzenie Steinera
I r 2 dm r 2 dm ( x a) 2 ( y b) 2 dm
m
m
m
x 2 2 xa a 2 y 2 2 yb b 2 dm
m
( x 2 y 2 )dm (2ax 2by)dm (a 2 b 2 )dm
m
m
m
R 2 dm (2ax 2by )dm D 2 dm
m
m
m
I MD 2
I I ' MD
2

14. Slajd 14

Moment bezwładności pręta względem osi
przechodzącej przez jego koniec
y
x
L
Moment bezwładności względem osi
przechodzącej przez środek masy:
1
I ' ML2
12
Odległość między osiami:
L
D
2
Zgodnie z twierdzeniem Steinera:
2
1
1
1
1
L
2
2
2
2
I I ' MD ML M ML ML ML2
12
4
3
2 12

15. Slajd 15

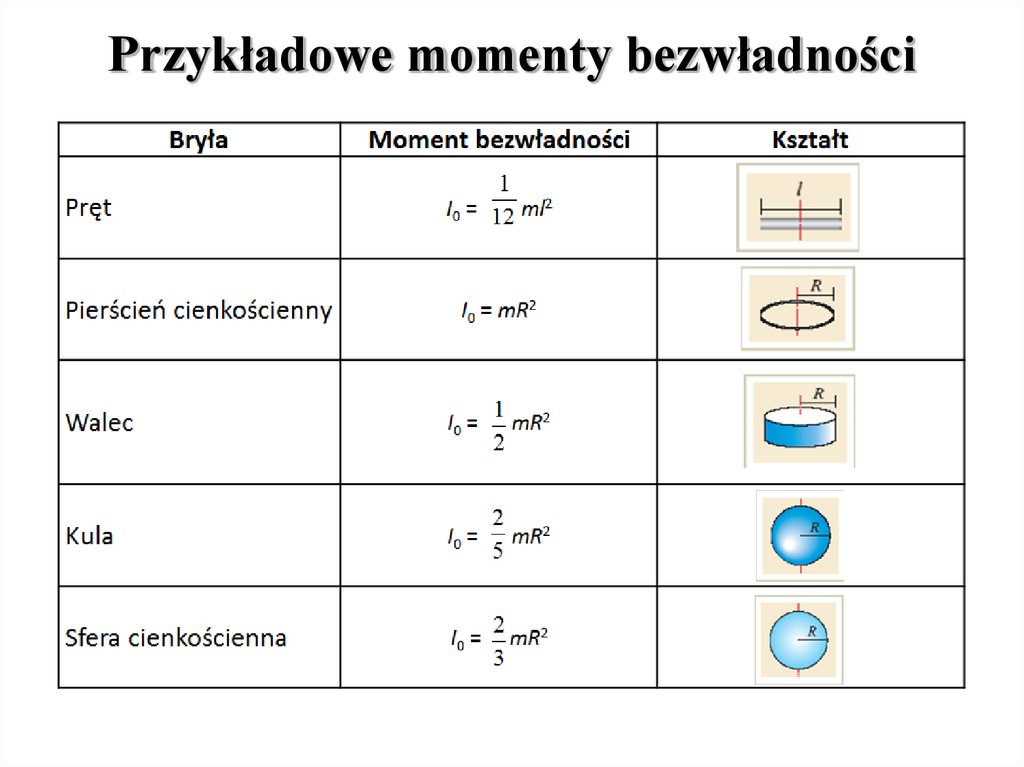
Przykładowe momenty bezwładności

16. Slajd 16

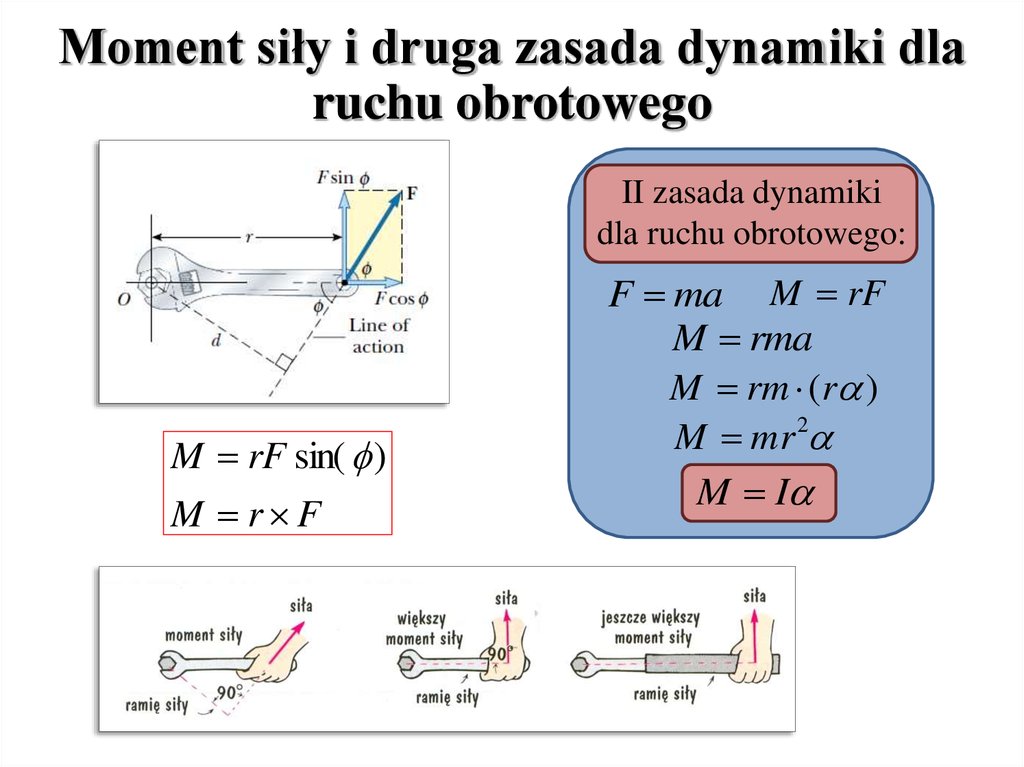
Moment siły i druga zasada dynamiki dla
ruchu obrotowego
II zasada dynamiki
dla ruchu obrotowego:
M rF sin( )
M r F
F ma M rF
M rma
M rm (r )
M mr 2
M I

17. Slajd 17

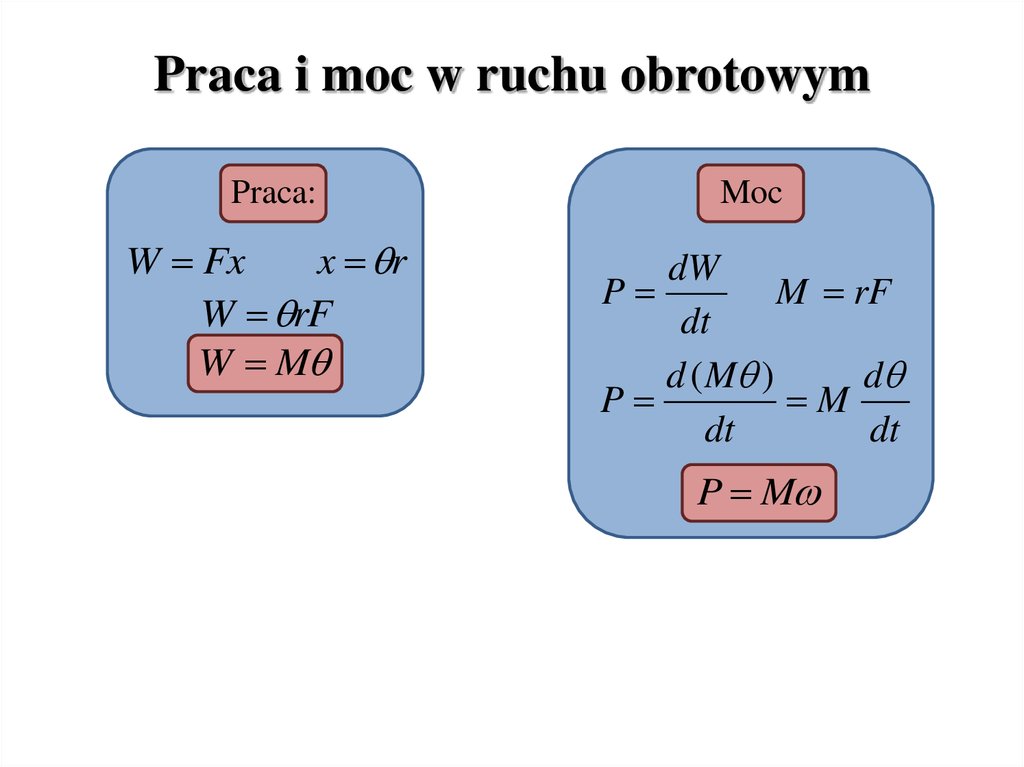
Praca i moc w ruchu obrotowym
Praca:
W Fx
x r
W rF
W M
Moc
dW
P
M rF
dt
d ( M )
d
P
M
dt
dt
P M

18. Slajd 18

Toczenie się ciał

19. Slajd 19

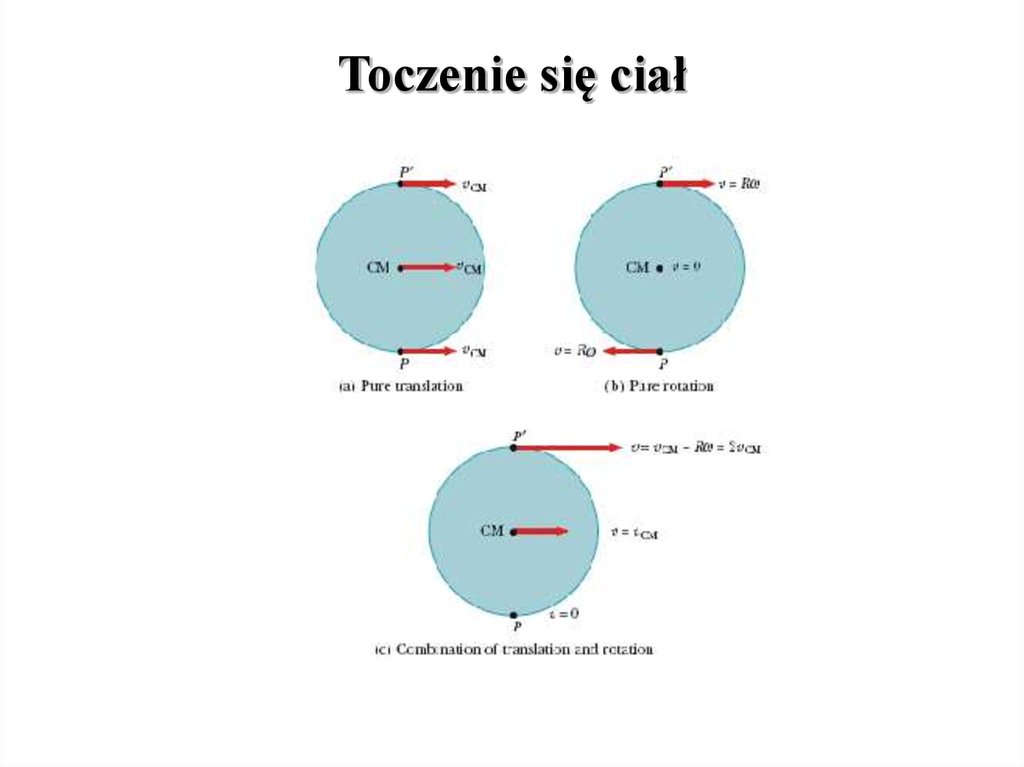
Toczenie się ciał

20. Slajd 20

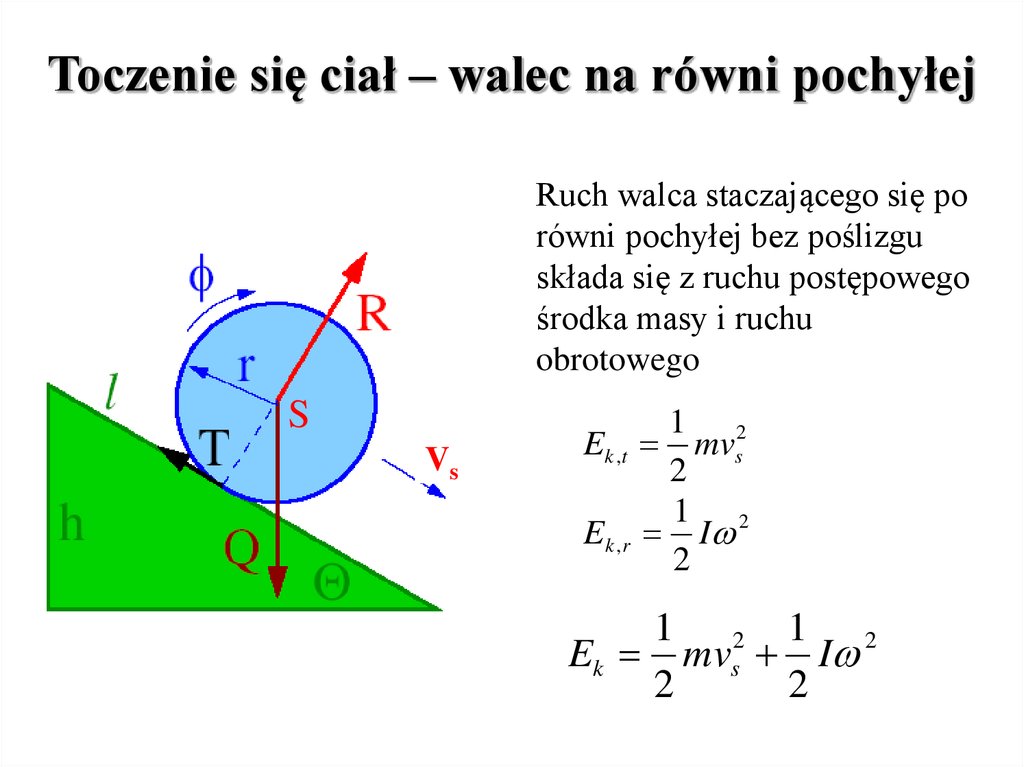
Toczenie się ciał – walec na równi pochyłej
Ruch walca staczającego się po
równi pochyłej bez poślizgu
składa się z ruchu postępowego
środka masy i ruchu
obrotowego
S
Vs
1 2
mvs
2
1 2
I
2
Ek ,t
Ek ,r
1 2 1 2
Ek mvs I
2
2

21. Slajd 21

Moment pędu
L rp
vi ri
n
n
L ri mi vi mi ri ri
i 1
i 1
a b c b a c c a b
z
L
n
L mi ri2 ri ri
p=mv
i 1
ri xi x yi y zi z
n
n
Lx x mi ri2 mi xi ri
i 1
i 1
n
n
Ly y mi ri mi yi ri
2
i 1
i 1
n
n
Lz z mi ri mi zi ri
2
i 1
i 1
x
r
y

22. Slajd 22

Moment pędu
n
Lx x mi ri x
i 1
2
2
i
m x y m x z
n
n
y
i
i
i
z
i 1
n
2
i 1
i 1
i i
i 1
Ly x mi xi yi y mi ri y
n
i
2
i
m y z
n
z
i 1
i
i i
Lz x mi xi zi y mi yi zi z mi ri 2 zi2
n
n
n
i 1
i 1
i 1
wprowadzając:
I xx mi ri 2 xi2
n
i 1
n
I xy mi xi2 yi2
i 1
n
I xz mi xi2 zi2
i 1
możemy powyższy układ równań zapisać
używając Tensora Bezwładności*:
Lx I xx
L I
y yx
Lz I zx
* wyrazy Tensora Bezwładności to momenty bezwładności
względem osi x, y, z oraz momenty dewiacji
I xy
I yy
I zy
I xz x
I yz y
I zz z
L Iˆ

23. Slajd 23

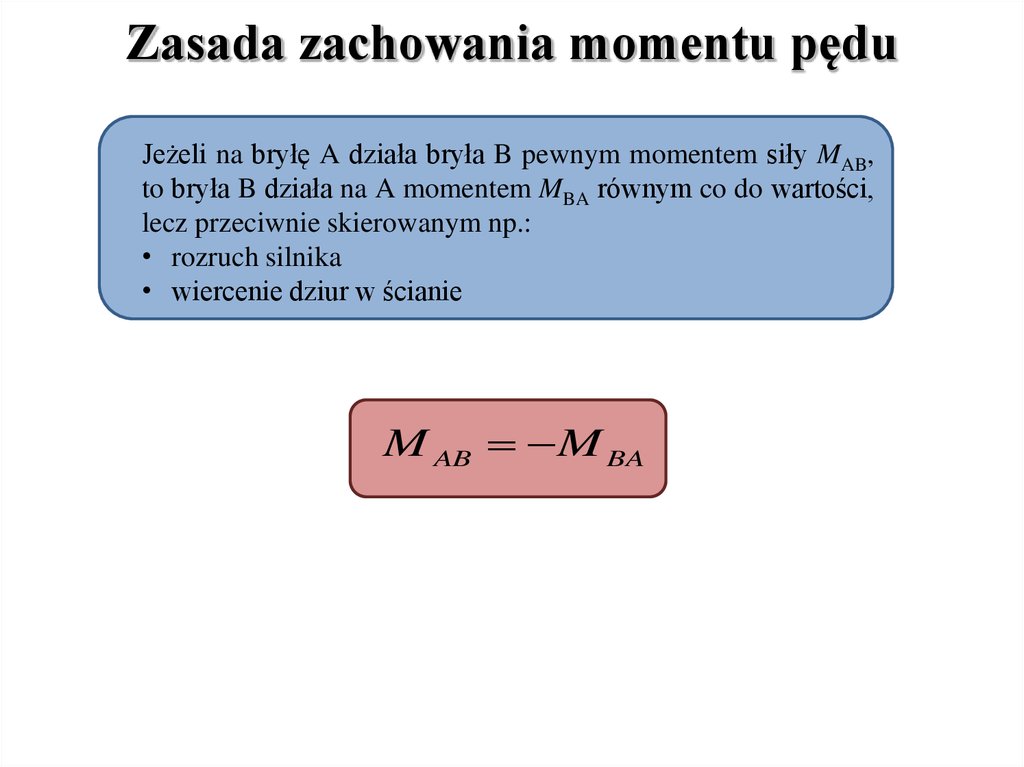
Zasada zachowania momentu pędu
Jeżeli na bryłę A działa bryła B pewnym momentem siły MAB,
to bryła B działa na A momentem MBA równym co do wartości,
lecz przeciwnie skierowanym np.:
• rozruch silnika
• wiercenie dziur w ścianie
M AB M BA

24. Slajd 24

Zasada zachowania momentu pędu
M
dL
dt
M 0
L const.
Obrotowy stołek: kręt układu
(człowiek + hantle) pozostaje
stały: zmniejszenie momentu
bezwładności wskutek zbliżenia
hantli przyspiesza obrót).
Skaczący gimnastyk
może zmieniać swoją
prędkość obrotową
przez odpowiednią
zmianę
momentu
bezwładności ciała,
gdyż moment pędu
musi być zachowany.

25. Slajd 25

Zasada zachowania momentu pędu
Ruch w polu siły centralnej.
(II prawo Keplera)
y
L const
p=mv
vdt
r
dS
1
r vdt sin
2
dS 1
1
1L
rv sin r v
dt 2
2
2m
x
dS 1 d 1 2
1 mr 2 1 L
r r
r
dt 2 dt 2
2 m
2m

26. Slajd 26

Analogie ruchu postępowego i obrotowego

27. Slajd 27

Staczanie się kuli po równi (bez poślizgu)
Ruch postępowy opisuje równanie:
ma Q sin T
ruch obrotowy (względem środka masy):
I Tr
eliminując siłę tarcia:
I
ma
mg sin
r
Miedzy przyspieszeniami
istnieje zależność:
a r
więc:
Im większy moment bezwładności, tym wolniej stacza się ciało.
g sin
a
I
1 2
mr

28. Slajd 28

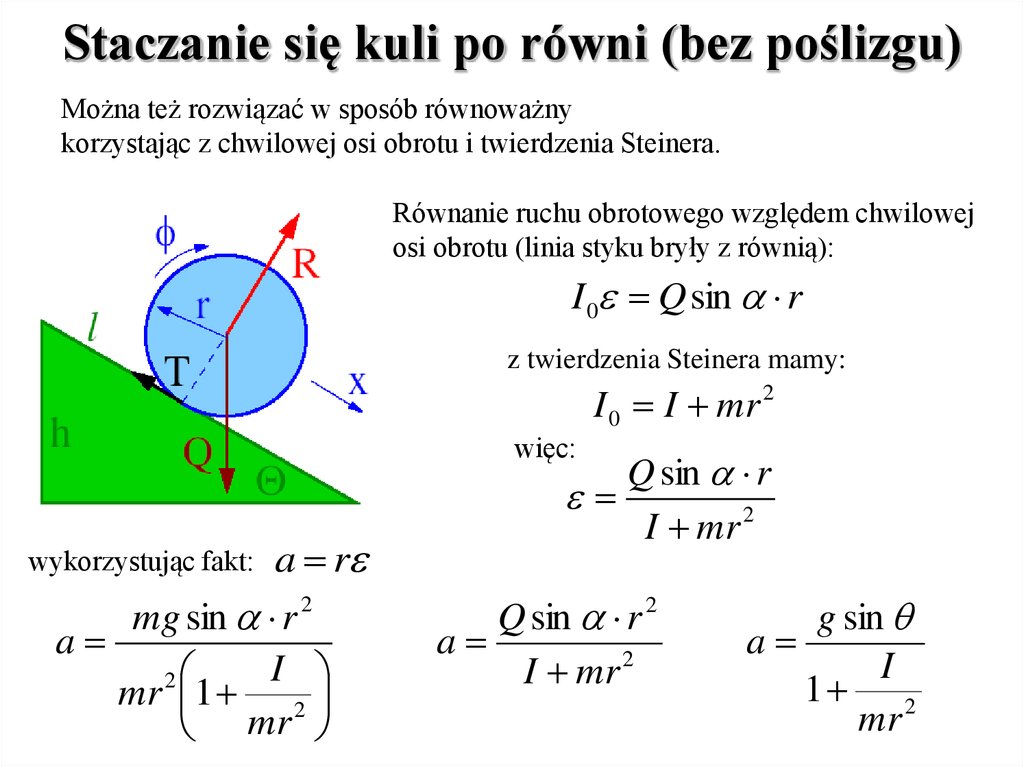
Staczanie się kuli po równi (bez poślizgu)
Można też rozwiązać w sposób równoważny
korzystając z chwilowej osi obrotu i twierdzenia Steinera.
Równanie ruchu obrotowego względem chwilowej
osi obrotu (linia styku bryły z równią):
I 0 Q sin r
z twierdzenia Steinera mamy:
I 0 I mr 2
więc:
a r
mg sin r 2
a
I
2
mr 1 2
mr
wykorzystując fakt:
Q sin r
I mr 2
Q sin r 2
a
I mr 2
g sin
a
I
1 2
mr

29. Slajd 29

Staczanie się ciał po równi (bez poślizgu)
1
2
I m r1 r22
2
1 2
I mr
2

30. Slajd 30

Zyroskop