Похожие презентации:
Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов
1.
Параллельные прямые.Признак параллельности
прямых по равенству
накрест лежащих углов
2.
Две прямые называются параллельными,если они не пересекаются.
a
b
Обозначают: a || b
3.
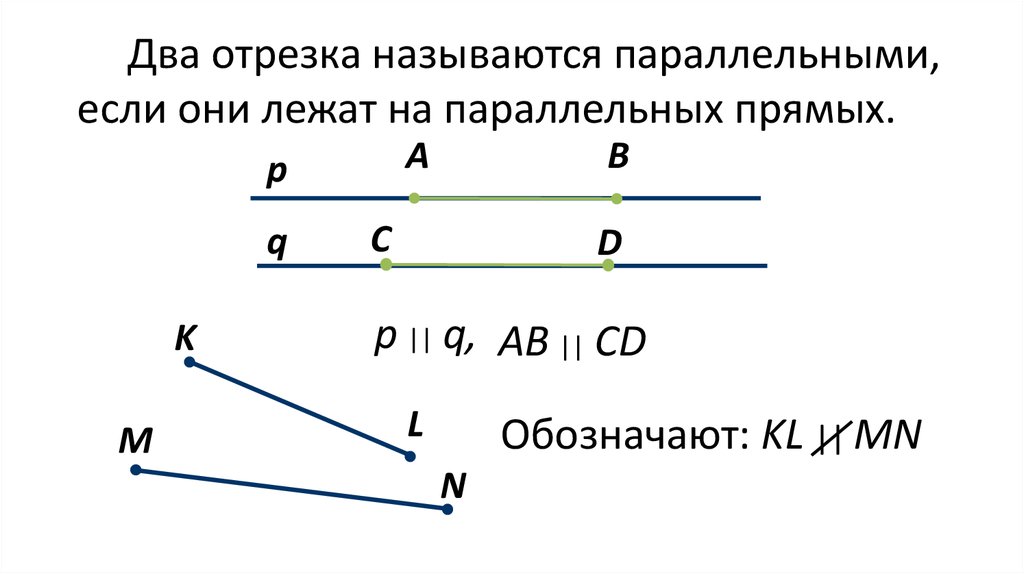
Два отрезка называются параллельными,если они лежат на параллельных прямых.
A
p
q
K
M
B
C
D
p || q, AB || CD
L
Обозначают: KL || MN
N
4.
QPQ || n
P
n
S
ST || EF
E
T
F
5.
ca
b
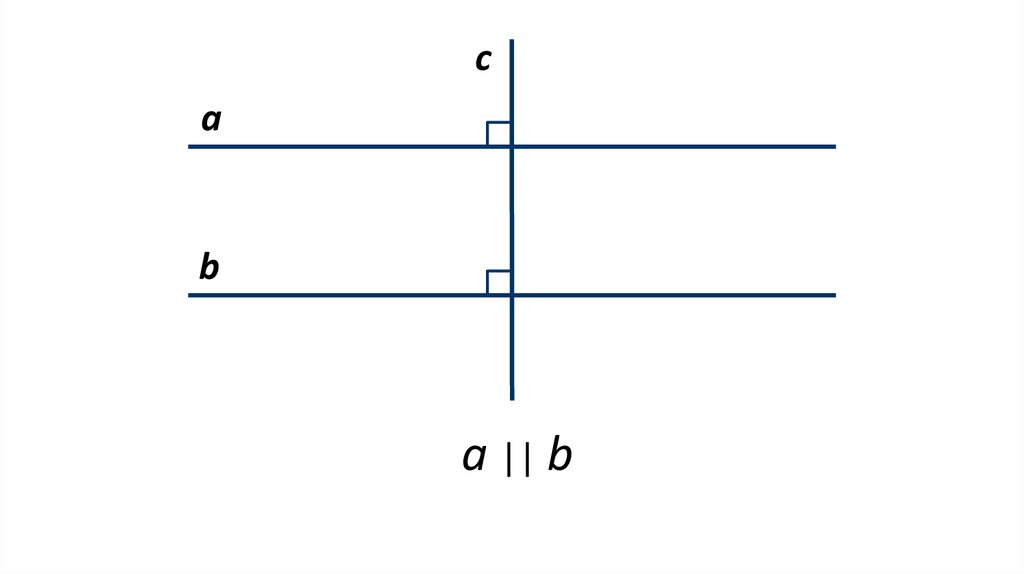
a || b
6.
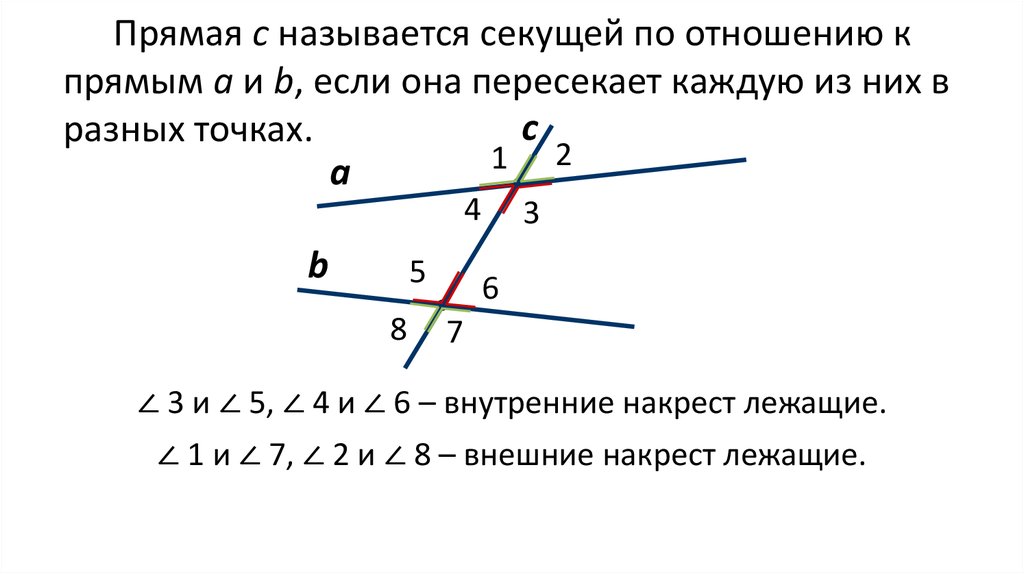
Прямая с называется секущей по отношению кпрямым а и b, если она пересекает каждую из них в
c
разных точках.
1 2
a
4
b
5
8
3
6
7
∠ 3 и ∠ 5, ∠ 4 и ∠ 6 – внутренние накрест лежащие.
∠ 1 и ∠ 7, ∠ 2 и ∠ 8 – внешние накрест лежащие.
7.
c1
a
3
4
b
5
8
2
6
7
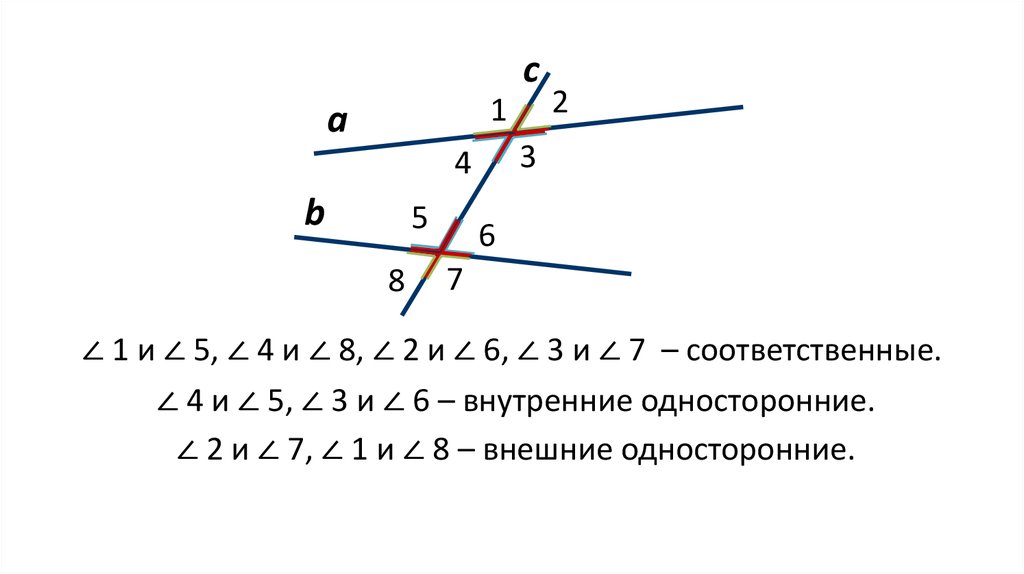
∠ 1 и ∠ 5, ∠ 4 и ∠ 8, ∠ 2 и ∠ 6, ∠ 3 и ∠ 7 – соответственные.
∠ 4 и ∠ 5, ∠ 3 и ∠ 6 – внутренние односторонние.
∠ 2 и ∠ 7, ∠ 1 и ∠ 8 – внешние односторонние.
8.
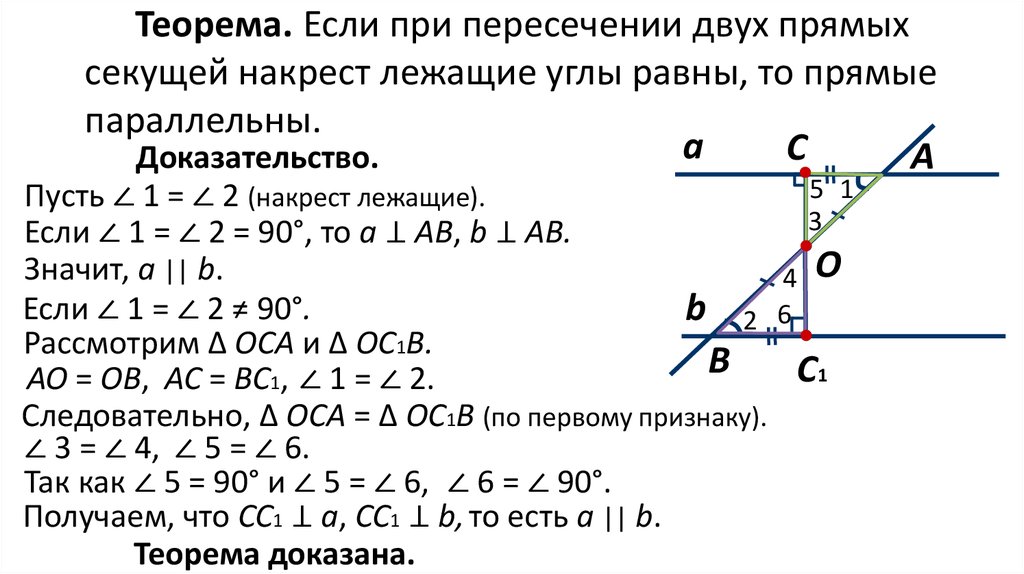
Теорема. Если при пересечении двух прямыхсекущей накрест лежащие углы равны, то прямые
параллельны.
a
С
Доказательство.
А
5 1
Пусть ∠ 1 = ∠ 2 (накрест лежащие).
3
Если ∠ 1 = ∠ 2 = 90°, то а ⊥ АВ, b ⊥ АВ.
Значит, а || b.
4 О
Если ∠ 1 = ∠ 2 ≠ 90°.
b 2 6
Рассмотрим ∆ ОСА и ∆ ОС1В.
В
С1
АО = ОВ, АС = ВС1, ∠ 1 = ∠ 2.
Следовательно, ∆ ОСА = ∆ ОС1В (по первому признаку).
∠ 3 = ∠ 4, ∠ 5 = ∠ 6.
Так как ∠ 5 = 90° и ∠ 5 = ∠ 6, ∠ 6 = ∠ 90°.
Получаем, что СС1 ⊥ а, СС1 ⊥ b, то есть а || b.
Теорема доказана.
9.
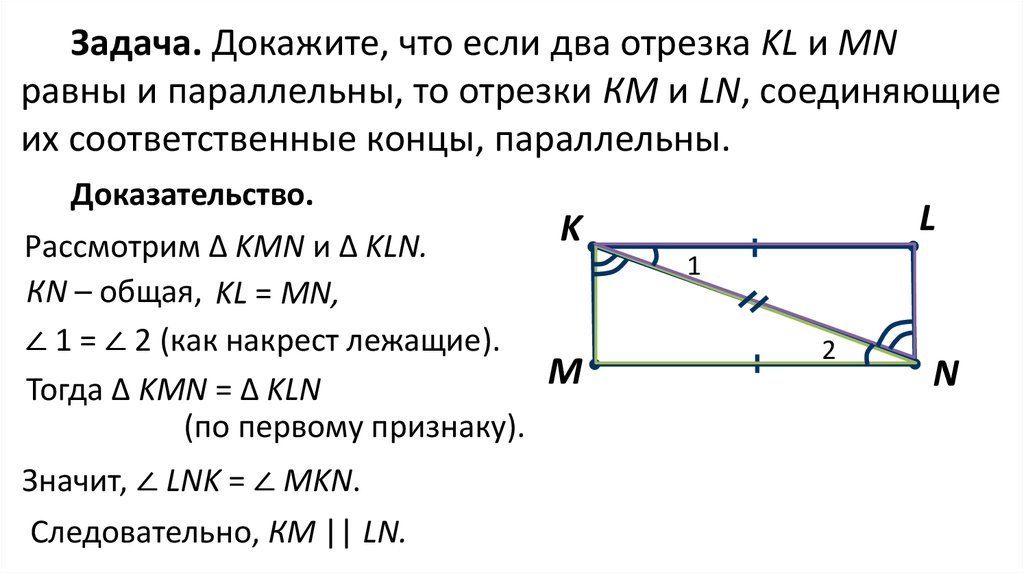
Задача. Докажите, что если два отрезка KL и MNравны и параллельны, то отрезки КМ и LN, соединяющие
их соответственные концы, параллельны.
Доказательство.
Рассмотрим ∆ KMN и ∆ KLN.
КN – общая, KL = MN,
∠ 1 = ∠ 2 (как накрест лежащие).
M
Тогда ∆ KMN = ∆ KLN
(по первому признаку).
Значит, ∠ LNK = ∠ MKN.
Следовательно, КМ || LN.
L
K
1
2
N
10.
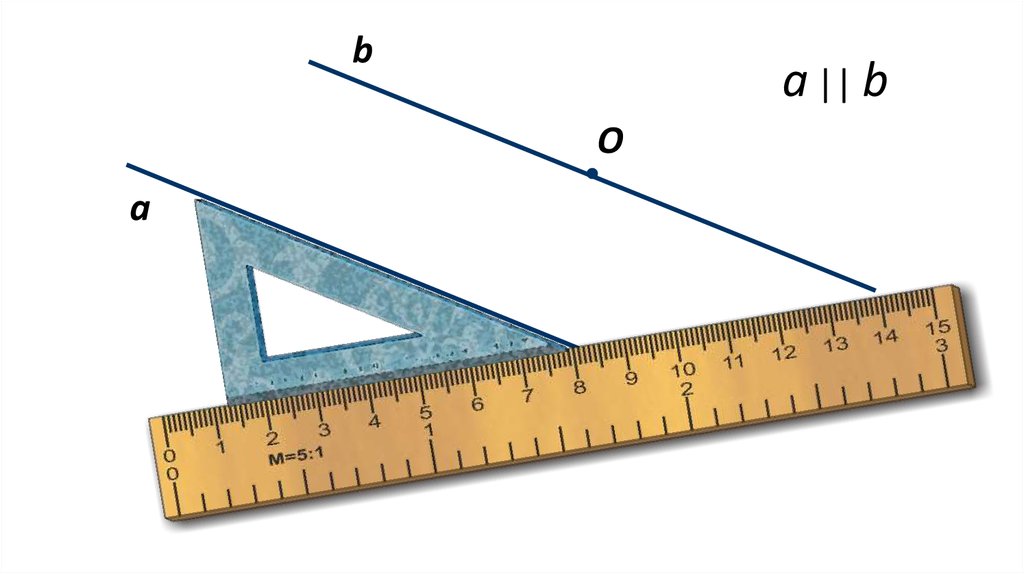
bа || b
О
a




 Математика
Математика








