Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов)

1. Анализ таблиц сопряжения.Меры эффекта в исследованиях (отношение рисков,шансов)

2.

• Таблица сопряжённости
• Таблица сопряжённости, или таблица контингентности, факторная
таблица в статистике — средство представления совместного
распределения двух переменных, предназначенное для
исследования связи между ними. Таблица сопряжённости
является наиболее универсальным средством изучения
статистических связей, так как в ней могут быть представлены
переменные с любым уровнем измерения. Таблицы
сопряжённости часто используются для проверки гипотезы о
наличии связи между двумя признаками с использованием
точного теста Фишера или критерия согласия Пирсона.

3.

• Многие задачи медицины могут быть решены с помощью статистики и все модули
системы STATISTICA, так или иначе, используются в медицине. Прежде всего, в
медицине статистика используется в задачах, связанных с выборочными
обследованиями, с проверкой эффективности различных доз различных лекарств,
диагностика заболеваний на основании проводимых медицинских анализов,
выявление сезонных факторов и скрытых периодичностей (например, определение
того, как рождаемость зависит от месяца или дня недели), оценка интенсивности
вызовов скорой помощи в зависимости от времени суток, прогнозирование
выздоровления больных, оценка зависимостей между различными переменными,
например, как состояние зубов детей связано со способом кормления (кормление
грудью или искусственное кормление) и т.д.
• Ситуация осложняется тем, что часто исследователь располагает неполными
данными (наблюдения могут быть цензурированными, например, пациент переведен
в другой госпиталь или выписан и связь с ним утеряна). Для анализа неполных
наблюдений применяются специальные статистические методы, реализованные в
модуле Анализ выживаемости.
• Кроме того, данные могут содержать много пропусков. Методы обработки
пропущенных значений доступны в любом модуле системы.

4.

• Если анализируются данные небольшого объема и нет никаких обоснованных предположений о
форме распределения наблюдаемых величин, применяются методы, реализованные в модуле
Непараметрическая статистика.
• Если нужно провести классификацию больных, описываемых несколькими признаками, то следует
использовать модуль Дискриминантный анализ. Однако методы дискриминантного анализа
"работают", если переменные измерены в достаточно богатой шкале, например, интервальной. Если
предикторы измерены в номинальной или порядковой шкале, то используют методы модуля Деревья
классификации.
• Для задач прогнозирования выздоровления пациентов применяются методы Множественной
регрессии. Однако во многих ситуациях приходится иметь дело с кусочно линейными моделями, т.к.
до определенного критического момента (например, спустя 23 дня после операции) адекватна одна
линейная модель и хороший прогноз дает одно подмножество предикторов. По прошествии
критического момента, модель меняется и меняется множество предикторов, позволяющих строить
прогноз. Методы модуля Нелинейное оценивание содержат необходимый инструментарий для
анализа таких задач.
• Специальные методы анализа многовходовых таблиц сопряженности реализованы в модулях
Логлинейный анализ и Анализ соответствий.
• Широкий круг задач может быть решен в модуле Основные статистики и таблицы.

5.

• Исследование эффективности прививок
• Рассмотрим следующий пример анализа в модуле Основные
статистики и таблицы.
• Предположим, вы хотите исследовать, как связаны прививка
против определенной болезни и заболеваемость этой болезнью.
Случайным образом вы выбираете истории болезней из архива и
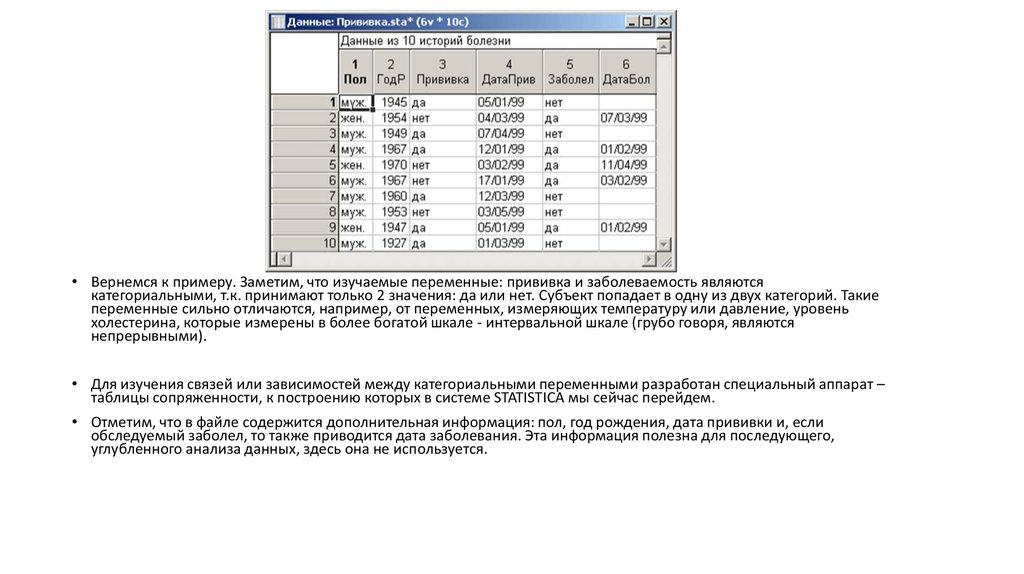
создаете файл данных, подобный тому как показан ниже:
• Вы хотите установить, как связаны два признака (и связаны ли
они вообще): прививка и заболеваемость.

6.

• Вернемся к примеру. Заметим, что изучаемые переменные: прививка и заболеваемость являются
категориальными, т.к. принимают только 2 значения: да или нет. Субъект попадает в одну из двух категорий. Такие
переменные сильно отличаются, например, от переменных, измеряющих температуру или давление, уровень
холестерина, которые измерены в более богатой шкале - интервальной шкале (грубо говоря, являются
непрерывными).
• Для изучения связей или зависимостей между категориальными переменными разработан специальный аппарат –
таблицы сопряженности, к построению которых в системе STATISTICA мы сейчас перейдем.
• Отметим, что в файле содержится дополнительная информация: пол, год рождения, дата прививки и, если
обследуемый заболел, то также приводится дата заболевания. Эта информация полезна для последующего,
углубленного анализа данных, здесь она не используется.

7.

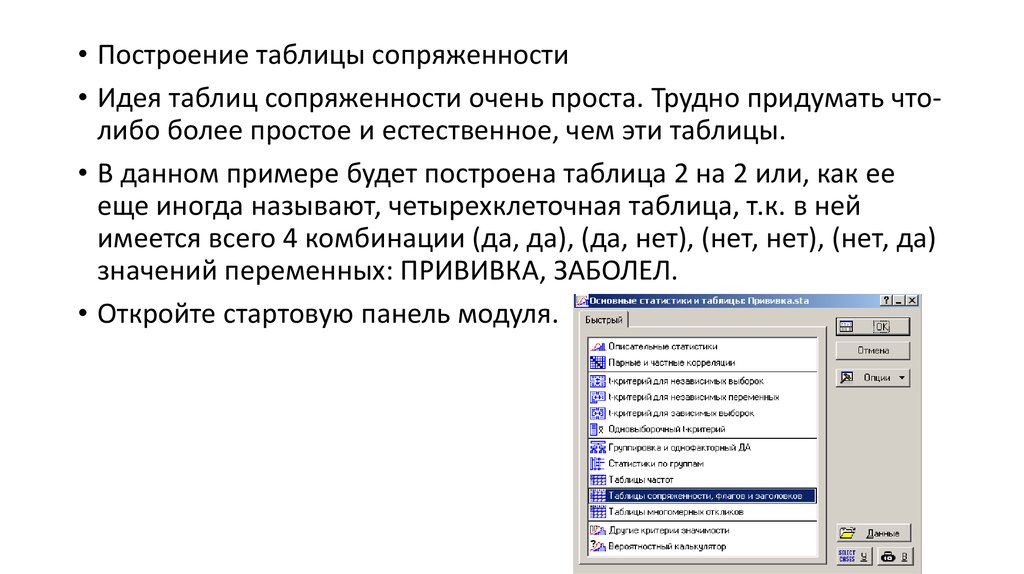
• Построение таблицы сопряженности
• Идея таблиц сопряженности очень проста. Трудно придумать чтолибо более простое и естественное, чем эти таблицы.
• В данном примере будет построена таблица 2 на 2 или, как ее
еще иногда называют, четырехклеточная таблица, т.к. в ней
имеется всего 4 комбинации (да, да), (да, нет), (нет, нет), (нет, да)
значений переменных: ПРИВИВКА, ЗАБОЛЕЛ.
• Откройте стартовую панель модуля.

8.

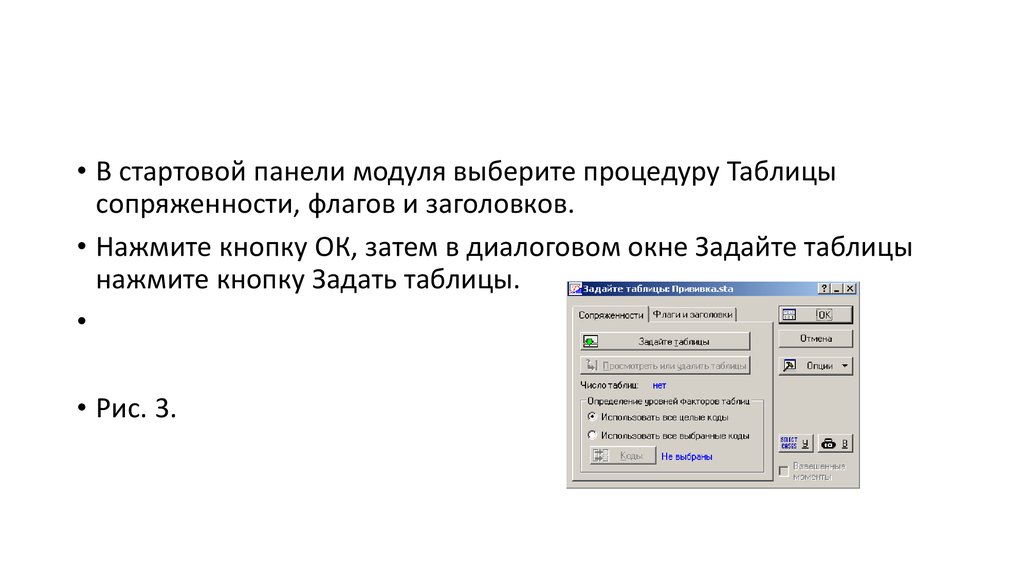
• В стартовой панели модуля выберите процедуру Таблицы
сопряженности, флагов и заголовков.
• Нажмите кнопку ОК, затем в диалоговом окне Задайте таблицы
нажмите кнопку Задать таблицы.
• Рис. 3.

9. Выберите переменные, как показано ниже:

10.

• Всего можно выбрать до 6 списков группирующих переменных
(т.е. тех переменных, которые задают разбиение пациентов на
группы), нам достаточно выбрать только 2 переменные. Нажмите
кнопку ОК. Вы снова вернетесь в диалоговое окно задания
таблицы, где следует нажать кнопку Коды.

11.

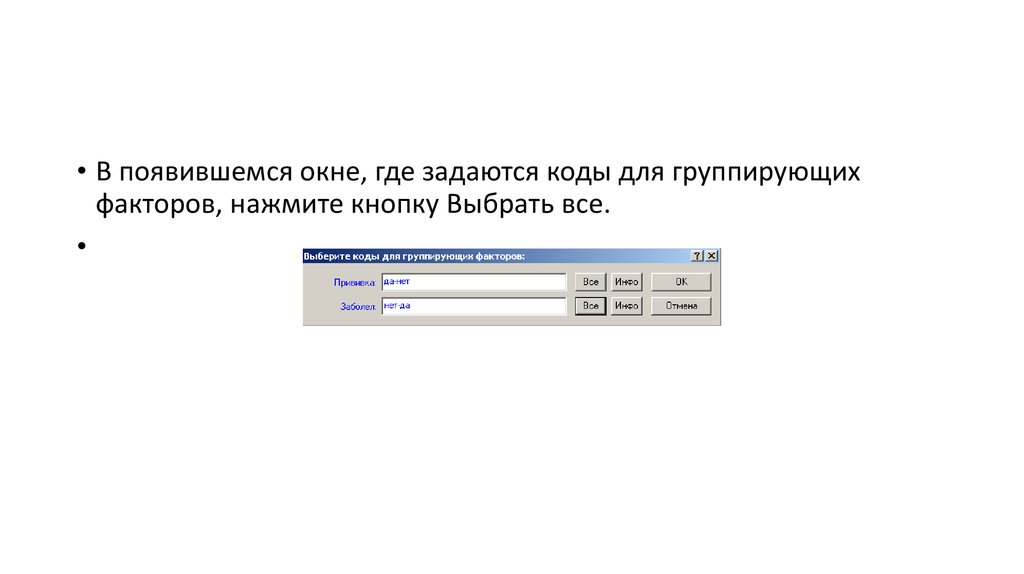
• В появившемся окне, где задаются коды для группирующих
факторов, нажмите кнопку Выбрать все.

12.

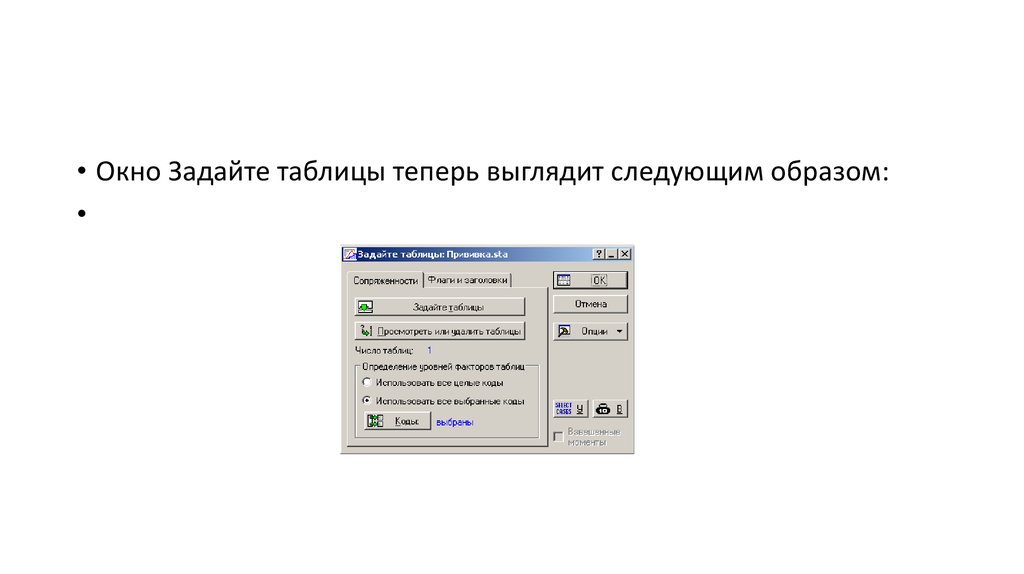
• Окно Задайте таблицы теперь выглядит следующим образом:

13.

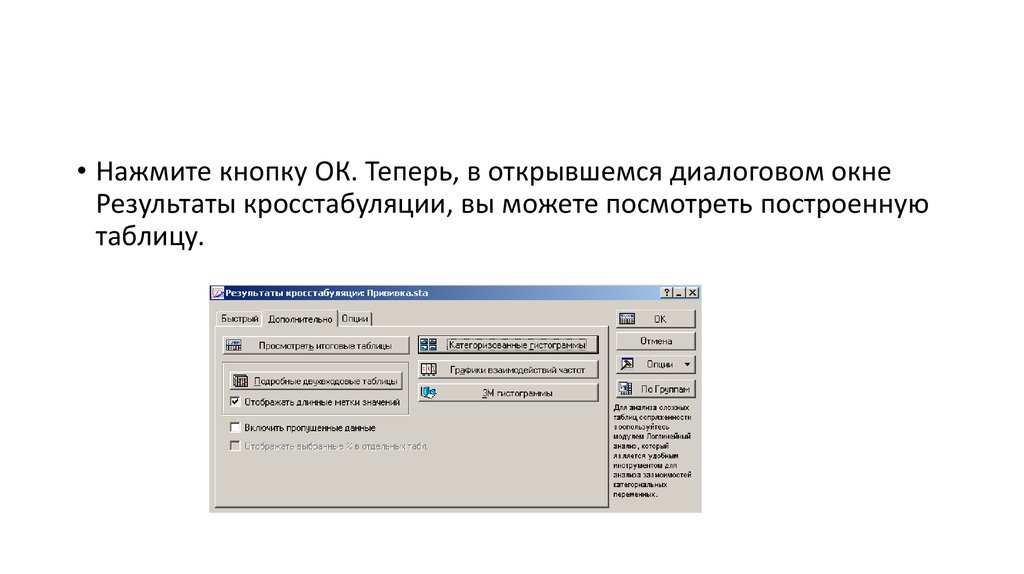
• Нажмите кнопку ОК. Теперь, в открывшемся диалоговом окне
Результаты кросстабуляции, вы можете посмотреть построенную
таблицу.

14.

• Нажмите кнопку Просмотреть итоговые таблицы и вы увидите
нужную таблицу сопряженности. Немного поупражнявшись, вы
научитесь строить таблицы сопряженности в системе за
несколько минут. Эта таблица содержит в сжатом виде всю
информацию, позволяющую оценить зависимость между
категориальными переменными: ПРИВИВКА, ЗАБОЛЕЛ.

15.

• Посмотрев на таблицу, вы видите, например, что 1 человек из
числа обследуемых – не имел прививок и не заболел (левая
верхняя клетка), 3 человека не имели прививок и заболели
(следующая клетка в первой строке), 4 человека имели прививки
и не заболели (первая клетка во второй строке), 2 человека имели
прививки и заболели (вторая клетка во второй строке).
• В нижней строке записаны суммы значений по столбцам. В
крайнем правом столбце – суммы значений по строкам. Эти
значения иногда называют маргинальными или краевыми, т.к.
они находятся на краях таблицы.

16.

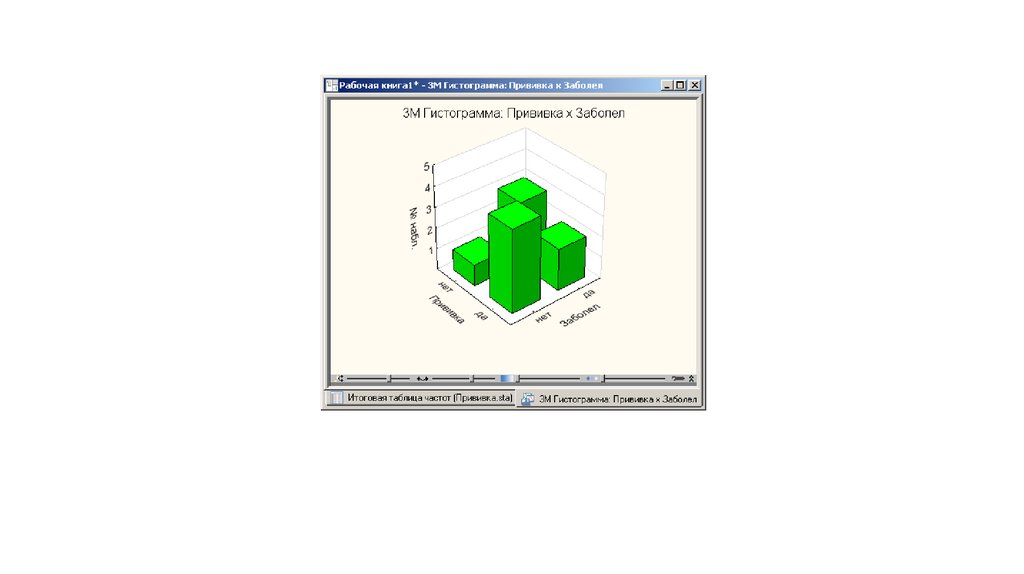
• Графическое представление таблиц сопряженности
• Посмотрим теперь на графическое представление данной
таблицы. Нажмите кнопку 3М гистограммы и вы увидите
гистограмму частот. Это 3-х мерная гистограмма частот.

17.

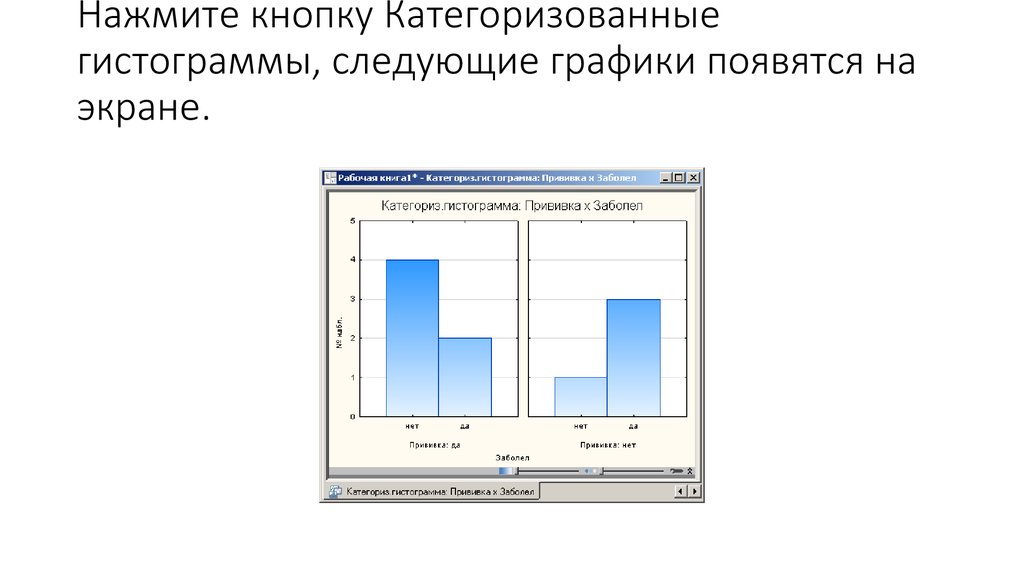
18. Нажмите кнопку Категоризованные гистограммы, следующие графики появятся на экране.

19.

• Каждый из этих графиков по-своему удобен и полезен, и мы
сейчас продемонстрируем это.
• Во втором, категоризованном графике, как вы видите, все
обследуемые разбиты на две категории (группы): ПРИВИВКА нет, ПРИВИВКА – да. Из графика видно, что число заболевших в
группе, несделавших прививки, больше числа заболевших в
группе, сделавших прививки.
• Если прививка не сделана, то число незаболевших 1, а число
заболевших 3. Если прививка сделана, то число незаболевших 4,
число заболевших 2.

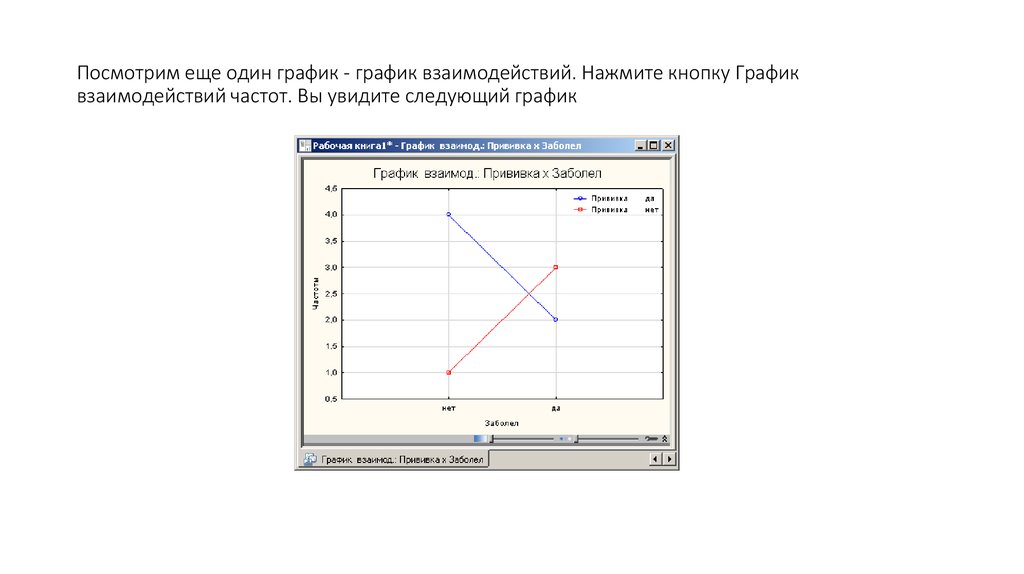
20. Посмотрим еще один график - график взаимодействий. Нажмите кнопку График взаимодействий частот. Вы увидите следующий график

21.

• Из графиков также видно, что число людей, сделавших прививки
и заболевших, меньше, числа людей не сделавших прививки и
заболевших. Прямые на графике пересекаются, следовательно
факторы взаимодействуют между собой.
• Итак, проявление зависимости между признаками на графике
взаимодействий – пересечение прямых.
• Если бы прямые были параллельны, мы бы сказали, что
взаимодействие между факторами отсутствует.

22.

• ОТНОШЕНИЕ ШАНСОВ
• ​Отношение шансов – статистический показатель (на русском его
название принято сокращать как ОШ, а на английском - OR от
"odds ratio"), один из основных способов описать в численном
выражении то, насколько отсутствие или наличие определённого
исхода связано с присутствием или отсутствием определённого
фактора в конкретной статистической группе.

23.

• 1. История разработки показателя отношения шансов
• Термин "шанс" пришел из теории азартных игр, где при помощи
данного понятия обозначали отношение выигрышных позиций к
проигрышным. В научной медицинской литературе показатель
отношения шансов был впервые упомянут в 1951 году в работе
Дж. Корнфилда. Впоследствие данным исследователем были
опубликованы работы, в которых отмечалась необходимость
расчета 95% доверительного интервала для отношения шансов.
(Cornfield, J. A Method for Estimating Comparative Rates from Clinical
Data. Applications to Cancer of the Lung, Breast, and Cervix // Journal
of the National Cancer Institute, 1951. - N.11. - P.1269–1275.)

24.

• 2. Для чего используется показатель отношения шансов?
• Отношение шансов позволяет оценить связь между
определенным исходом и фактором риска.
• Отношение шансов позволяет сравнить группы исследуемых по
частоте выявления определенного фактора риска. Важно, что
результатом применения отношения шансов является не только
определение статистической значимости связи между фактором
и исходом, но и ее количественная оценка.

25.

• 3. Условия и ограничения применения отношения шансов
• Результативные и факторные показатели должны быть измерены в номинальной шкале.
Например, результативный признак - наличие или отсутствие врожденного порока развития
у плода, изучаемый фактор - курение матери (курит или не курит).
• Данный метод позволяет проводить анализ только четырехпольных таблиц, когда и фактор,
и исход являются бинарными переменными, то есть имеют только два возможных значения
(например, пол - мужской или женский, артериальная гипертония - наличие или отсутствие,
исход заболевания - с улучшением или без улучшения...).
• Сопоставляемые группы должны быть независимыми, то есть показатель отношения
шансов не подходит для сравнения наблюдений "до-"после".
• Показатель отношения шансов используется в исследованиях по типу "случай-контроль"
(например, первая группа - больные гипертонической болезнью, вторая - относительно
здоровые люди). Для проспективных исследований, когда группы формируются по признаку
наличия или отсутствия фактора риска (например, первая группа - курящие, вторая группа некурящие), обычно рассчитывается относительный риск.

26.

• 4. Как рассчитать отношение шансов?
• Отношение шансов – это значение дроби, в числителе которой,
находятся шансы определённого события для первой группы, а в
знаменателе шансы того же события для второй группы.
• Шансом является отношение числа исследуемых, имеющих
определенный признак (исход или фактор), к числу исследуемых, у
которых данный признак отсутствует.
• Например, была отобрана группа пациентов, прооперированных по
поводу панкреонекроза, число которых составило 100 человек. Через 5
лет из их числа в живых осталось 80 человек. Соответственно, шанс
выжить составил 80 к 20, или 4,0.
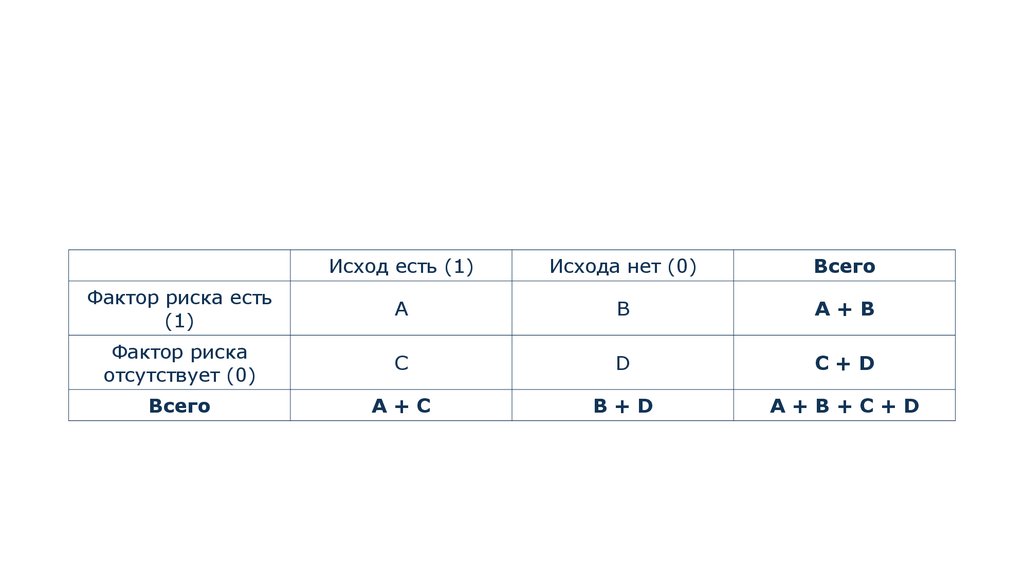
• Удобным способом является расчёт отношения шансов со сведением
данных в таблицу 2х2:

27.

Исход есть (1)
Исхода нет (0)
Всего
Фактор риска есть
(1)
A
B
A+B
Фактор риска
отсутствует (0)
C
D
C+D
Всего
A+C
B+D
A+B+C+D

28.

• Для данной таблицы отношение шансов рассчитывается по следующей формуле:
• Очень важно оценить статистическую значимость выявленной связи между исходом и фактором
риска. Связано это с тем, что даже при невысоких значениях отношения шансов, близких к единице,
связь, тем не менее, может оказаться существенной и должна учитываться в статистических выводах.
И наоборот, при больших значениях OR, показатель оказывается статистически незначимым, и,
следовательно, выявленной связью можно пренебречь.
• Для оценки значимости отношения шансов рассчитываются границы 95% доверительного интервала
(используется абрревиатура 95% ДИ или 95% CI от англ. "confidence interval"). Формула для
нахождения значения верхней границы 95% CI:
• Формула для нахождения значения нижней границы 95% CI:

29. 5. Как интерпретировать значение отношения шансов?

• Если отношение шансов превышает 1, то это означает, что шансы обнаружить фактор риска больше в
группе с наличием исхода. Т.е. фактор имеет прямую связь с вероятностью наступления исхода.
• Отношение шансов, имеющее значение меньше 1, свидетельствует о том, что шансы обнаружить
фактор риска больше во второй группе. Т.е. фактор имеет обратную связь с вероятностью наступления
исхода.
• При отношении шансов, равном единице, шансы обнаружить фактор риска в сравниваемых группах
одинакова. Соответственно, фактор не оказывает никакого воздействия на вероятность исхода.
• Дополнительно в каждом случае обязательно оценивается статистическая значимость отношения
шансов исходя из значений 95% доверительного интервала.
• Если доверительный интервал не включает 1, т.е. оба значения границ или выше, или ниже 1,
делается вывод о статистической значимости выявленной связи между фактором и исходом при
уровне значимости p<0,05.
• Если доверительный интервал включает 1, т.е. его верхняя граница больше 1, а нижняя - меньше 1,
делается вывод об отсутствии статистической значимости связи между фактором и исходом при
уровне значимости p>0,05.
• Величина доверительного интервала обратно пропорциональна уровню значимости связи фактора и
исхода, т.е. чем меньше 95% ДИ, тем более существенной является выявленная зависимость.

30.

• 6. Пример расчета показателя отношения шансов
• Представим две группы: первая состояла из 200 женщин, у
которых был диагностирован врожденный порок развития плода
(Исход+). Из них курили во время беременности (Фактор+) - 50
человек (А), являлись некурящими (Фактор-) - 150 человек (С).
• Вторую группу составили 100 женщин без признаков ВПР плода
(Исход -) среди которых курили во время беременности (Фактор+)
10 человек (B), не курили (Фактор-) - 90 человек (D).
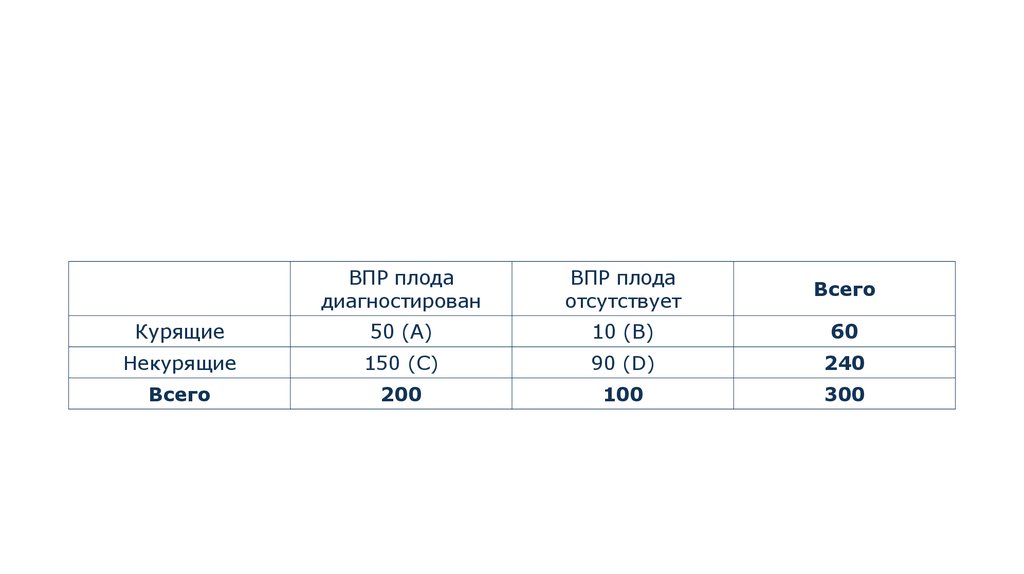
• 1. Составим четырехпольную таблицу сопряженности:

31.

ВПР плода
диагностирован
ВПР плода
отсутствует
Всего
Курящие
50 (А)
10 (В)
60
Некурящие
150 (С)
90 (D)
240
Всего
200
100
300

32.

• 2. Рассчитаем значение отношения шансов:
• OR = (A * D) / (B * C) = (50 * 90) / (150 * 10) = 3.
• 3. Найдем границы 95% CI. Значение нижней границы, рассчитанной
по указанной выше формуле составило 1,45, а верхней - 6,21.
• Таким образом, исследование показало, что шансы встретить курящую
женщину среди пациенток с диагностированным ВПР плода в 3 раза
выше, чем среди женщин без признаков ВПР плода. Наблюдаемая
зависимость является статистически значимой, так как 95% CI не
включает 1, значения его нижней и верхней границ больше 1.

33. Спасибо за внимание