Похожие презентации:
Неустойчивость тонких пленок, самоорганизация на поверхности
1. Наномеханика Nanomechanics of materials and systems
Lecture 5Неустойчивость тонких пленок,
само-организация на поверхности.
Surface instability and selforganization
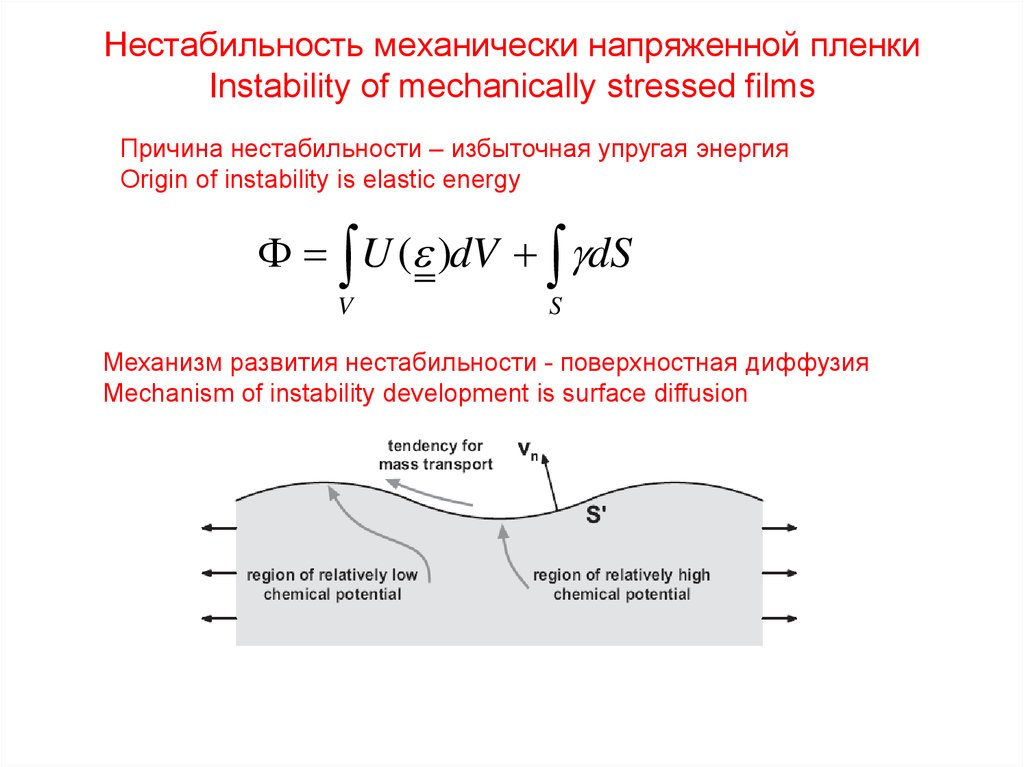
2. Нестабильность механически напряженной пленки Instability of mechanically stressed films
Причина нестабильности – избыточная упругая энергияOrigin of instability is elastic energy
U ( )dV dS
V
S
Механизм развития нестабильности - поверхностная диффузия
Mechanism of instability development is surface diffusion
3. Малые периодические изменения толщины Small periodic variation of thickness
ω=2π/λn ( n x , n y ); n x
h
a sin x o 2a 2 ; n y 1 o 2a 2
x
n 0
Плоская задача. РРешени с помощью функций Айри.
2 A
2 A
2 A
Plane strain. Solving via Airy stress function. σ xx 2 ; σ yy 2 ; σ xy
y
x
x y
1
(1) ( 2 ) ; 4 A 0; A(1) m y 2 xx(1) m ; yy(1) xy(1) 0
2
4. Малые периодические изменения толщины Small periodic variation of thickness
4 A( x, y ) 0; ( 2 ) 0 as yA( 2 ) ( c0 c1 y )a m exp ( y h ) cos x
A( 2 ) a m ( y h ) exp ( y h ) cos x
xx( 2 ) 2 A y 2 2 2 ( y h ) a m exp ( y h ) cos x
yy( 2 ) 2 A x 2 a m ( y h ) 2 exp ( y h ) cos x
xy( 2 ) 2 A x y a m 2 ( y h ) exp ( y h ) sin x
Граничные ууслови (Boundary conditions ) y h :
t x( 2 ) xx( 2 ) n x xy( 2 ) n y a m sin x o( a 2 2 )
(2)
t (y2 ) xy( 2 ) n x yy
n y 0 o( a 2 2 )
t x(1) xx(1) n x a m sin x o( a 2 2 )
t (y1) 0 o( a 2 2 )
5. Плотность энергии и химический потенциал Energy and chemical potential
Плоская задача ( plane strain )1 (2)
(1 ) ( 2 )
xx (1 2 ) yy( 2 ) (1 ) ; xy( 2 )
xy
E
E
Изменение ээнерги деформации вдоль поверхности ( Deformation energy along x )
zz( 2 ) 0; zz( 2 ) ( xx( 2 ) yy( 2 ) ); xx( 2 )
U ( x)
(1)
(2)
m2 (1 v 2 )
Ef
m2 (1 v ) 4 a
2 x
2a cos x
cos
Mf
Увеличение площади поверхности квадратично по a / λ (change in surface area)
2
h( x, t )
2 a
2 2 x
1
2
sin
2
2
x
Кривизна поверхности ( curvature of surface)
2
2h ( x, t )
2 x
2 a
4
cos
x 2
2
Химический потенциал (Chemical potential)
a
m2
U U m 4 (1 )
Mf
2 x
cos
6. Критическая длина стабильности Critical length of stability
Пусть a зависит от времениИзменение свободной энергии, усредненное по периоду λ:
Free energy over a period
vn dx 2 aa (1 )U m
0
Критическая длина периода (Critical period )
с
M
(1 ) m2 (1 ) M m2
Нестабильность Азаро-Тиллера—Гринфельда
Asaro-Tiller-Grinfeld instability
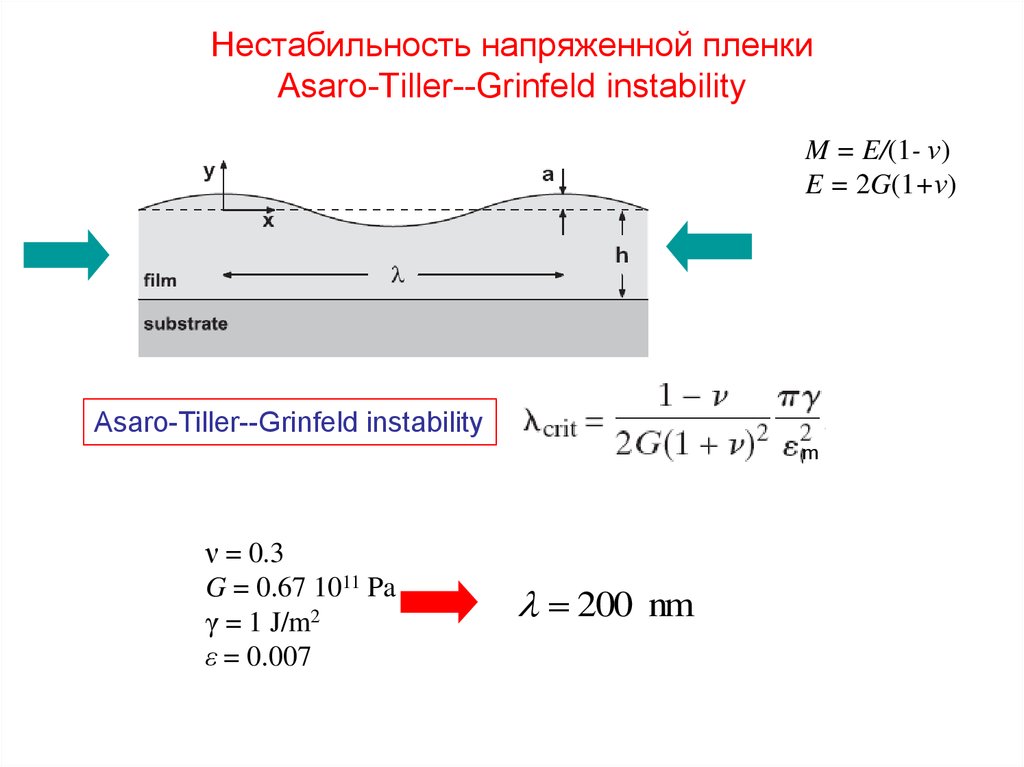
7. Нестабильность напряженной пленки Asaro-Tiller--Grinfeld instability
M = E/(1- ν)E = 2G(1+ν)
Asaro-Tiller--Grinfeld instability
m
ν = 0.3
G = 0.67 1011 Pa
γ = 1 J/m2
ε = 0.007
200 nm
8. Нестабильность пленки GeSi на Si Asaro-Tiller--Grinfeld instability of GeSi on Si
aTransmission electron microscopy cross-sectional image of a Si0:81Ge0:19 alloy
film grown epitaxially on a Si substrate (a). The ridges are aligned with a <100>
crystallographic direction. While the TEM image appears to represent a fully twodimensional configuration, the planview images of the film surface (b) shows that
the regular ordering has a relatively short range. The normal distance between
parallel lines in the lower images is the peak-to-peak distance in the upper
image, or about 300nm. Reproduced from Cullis et al. (1992). m=0.66%
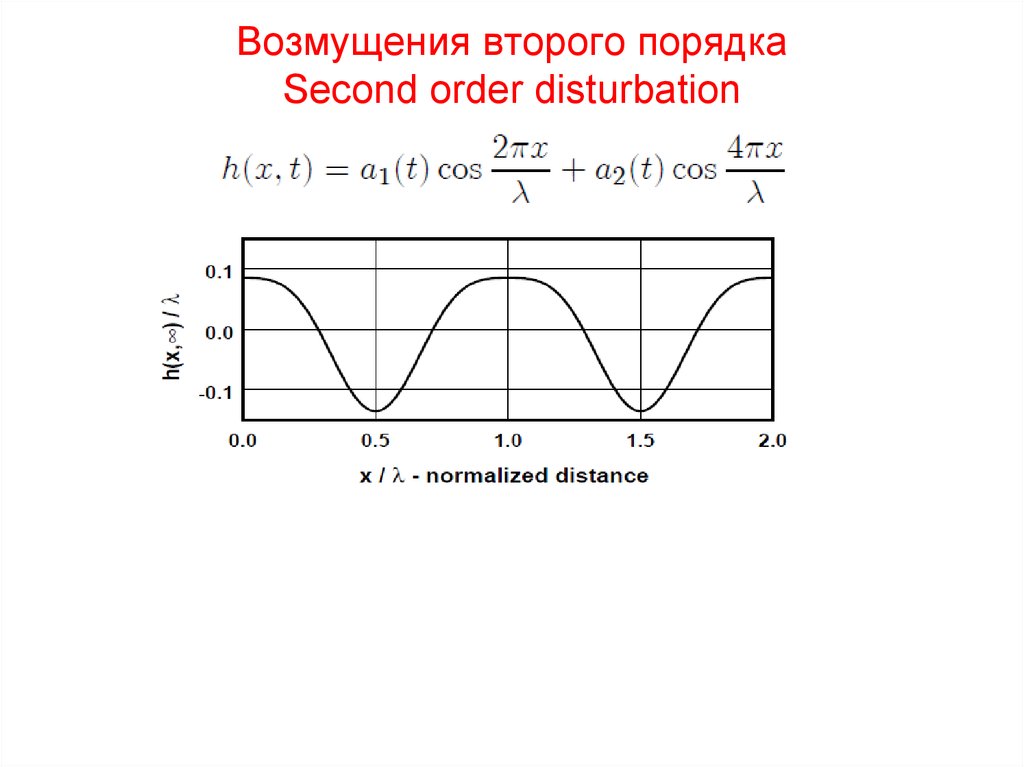
9. Возмущения второго порядка Second order disturbation
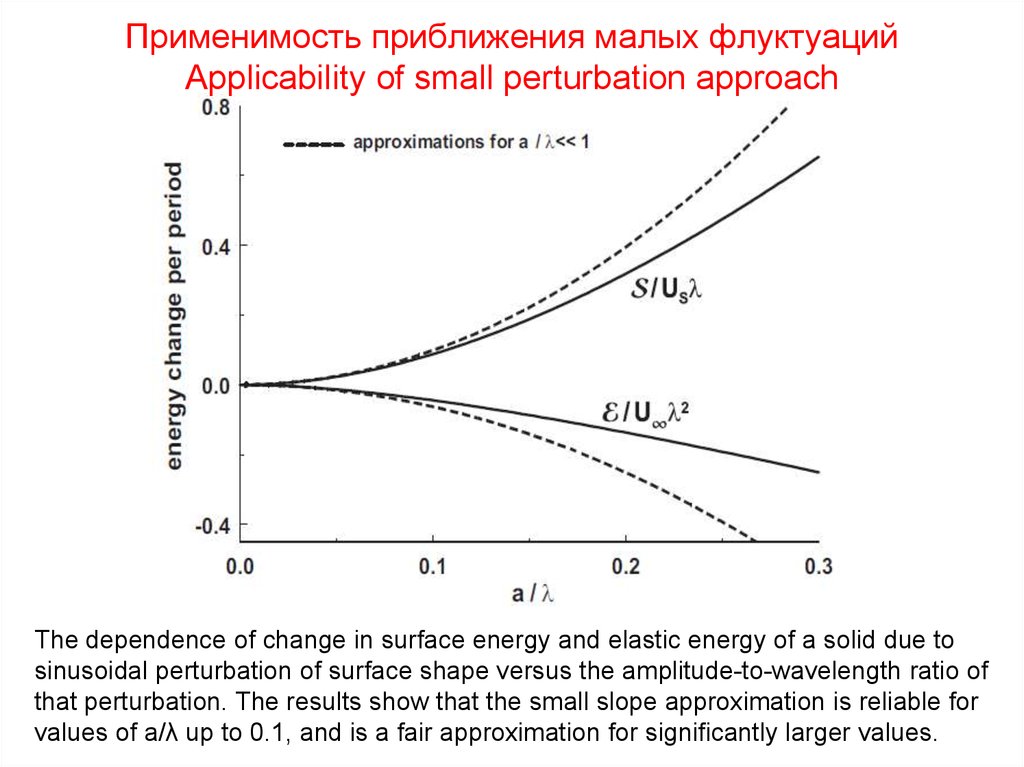
10. Применимость приближения малых флуктуаций Applicability of small perturbation approach
The dependence of change in surface energy and elastic energy of a solid due tosinusoidal perturbation of surface shape versus the amplitude-to-wavelength ratio of
that perturbation. The results show that the small slope approximation is reliable for
values of a/λ up to 0.1, and is a fair approximation for significantly larger values.
11. Домашнее задание (Homework) 4
Пленка Ge толщиной 4 нм выращенаэпитаксиально на подложке Si с ориентацией (111)
и толщиной 400 мкм.
4-nm-thick Ge epitaxial film was grown over 400-μmthick Si substrate with (111) orientation.
Определить (determine)
1. Анизотропию кривизны структуры по Стони
Anisotropy of Stoney curvature (if any?)
2. Критическую длину Asaro-Tiller-Grinfeld
нестабильности пленки (γ = 1 J/m2).
Asaro-Tiller-Grinfeld critical length (γ = 1 J/m2).
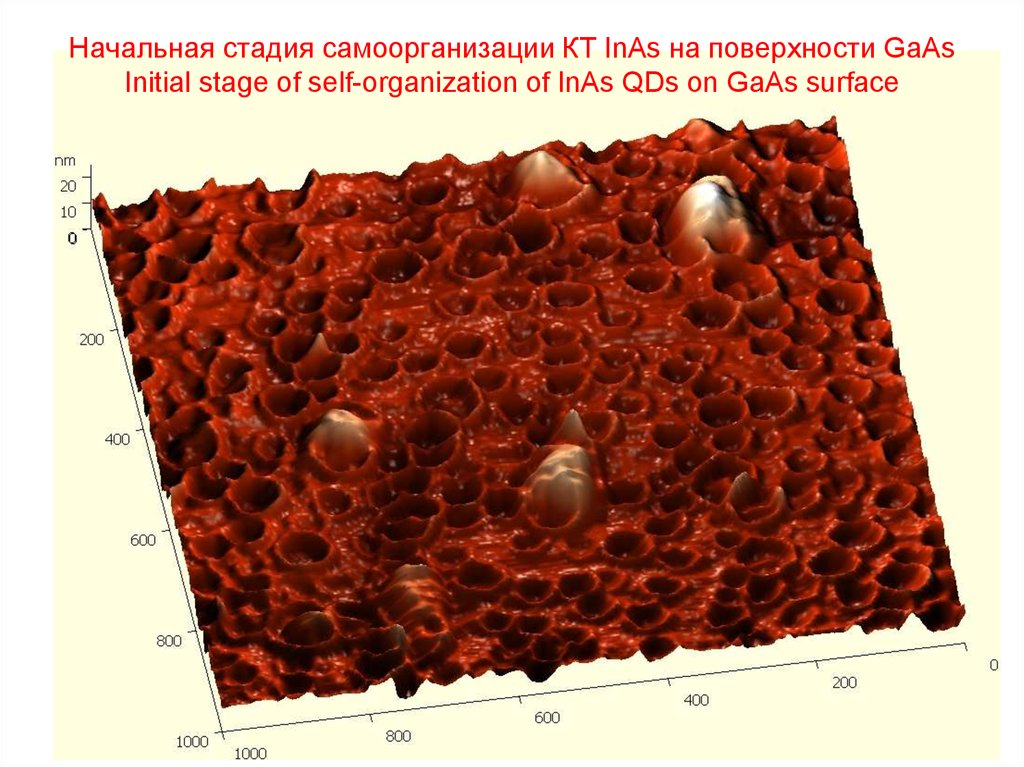
12. Начальная стадия самоорганизации КТ InAs на поверхности GaAs Initial stage of self-organization of InAs QDs on GaAs surface
13. КТ InAs на поверхности GaAs InAs quantum dots on GaAs surface
AFM image14. Причина формирования КТ – выигрыш в упругой энергии The reason for self-organization is a release of elastic energy
Effect of island shape on the volume elastic relaxation of acoherently strained island. The dark area is that with a large elastic
strain energy density: (a) island with height-to-width
ratio h/L<<1 is weakly relaxed; (b) island with height-to-width ratio
h/L>>1 is nearly completely relaxed.
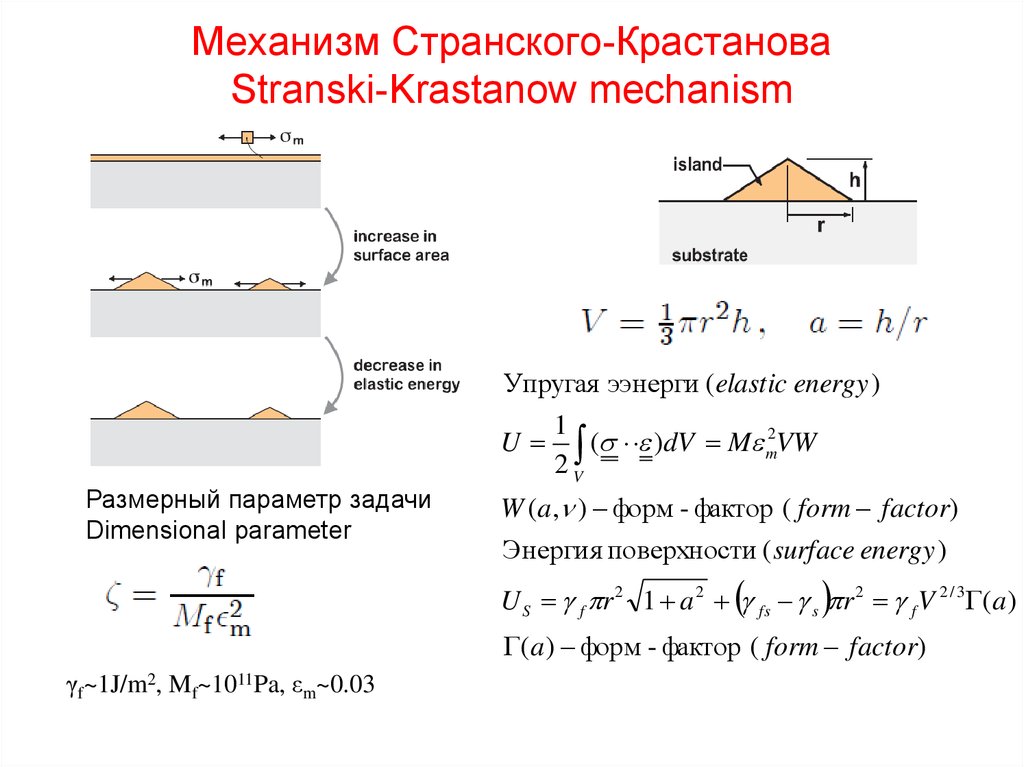
15. Механизм Странского-Крастанова Stranski-Krastanow mechanism
Упругая ээнерги ( elastic energy )U
Размерный параметр задачи
Dimensional parameter
1
2
(
)
dV
M
VW
m
2V
W ( a, ) форм - фактор ( form factor)
Энергия поверхности ( surface energy )
U S f r 2 1 a 2 fs s r 2 f V 2 / 3 ( a )
( a ) форм - фактор ( form factor)
γf~1J/m2, Mf~1011Pa, εm~0.03
16. Механизм Странского-Крастанова Stranski-Krastanow mechanism
dimensionless parameter17. Соотношение вертикального и латерального размеров Optimal aspect ratio
Free energy change per unit volume of island of material due to reorganizationof uniformly strained film material to a nonuniformly strained conical island.
The parameter Z = ζ/V1/3 represents the size of the island relative to the natural
system length ζ.
18. Упругая энергия при изменении отношения высоты островка к его основанию Elastic energy vs. aspect ratio
Начальные стадии формирования пирамид Ge на SiInitial stages of formation of Ge islands on Si
STM images of the
surface evolution during
growth of a Ge layer on
Si (001). In panels (a)–
(d), the Ge coverage
grows from 2.8 to 4.0
ML’s. During growth (a)–
(c) first mounds
(prepyramids) develop,
then these convert (d) to
{105} facetted pyramids.
From Vailionis et al.,
2000.
19. Начальные стадии формирования пирамид Ge на Si Initial stages of formation of Ge islands on Si
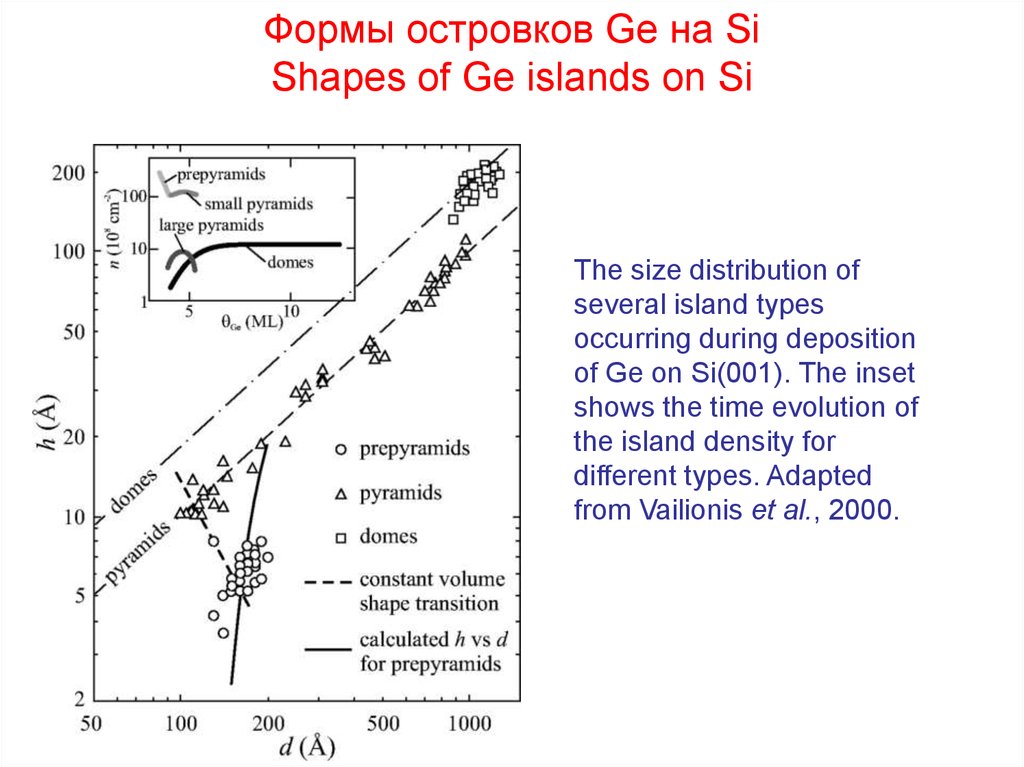
Формы островков Ge на SiShapes of Ge islands on Si
The size distribution of
several island types
occurring during deposition
of Ge on Si(001). The inset
shows the time evolution of
the island density for
different types. Adapted
from Vailionis et al., 2000.
20. Формы островков Ge на Si Shapes of Ge islands on Si
Распределение по размерамSize distribution
0
1
2
Size distributions of domes and pyramids calculated by means of
equilibrium statistics (lines) for two different Ge coverages Q, and
obtained from AFM (black dots). From Rudd et al., 2003
21. Распределение по размерам Size distribution
Эволюция формыShape evolution
Shape transition of Ge or SiGe islands grown on Si(001) during growth solid arrows,
postgrowth annealing (dotted arrow), and Si capping (dashed arrow). The solid
curves represent the critical volumes for pyramids and domes. From Rastelli,
Kummer, and von Kaenel, 2002.
22. Эволюция формы Shape evolution
Формы островковShape evolution
Typical Ge island shapes obtained by STM during Si capping of Ge domes
grown on Si(001): (a),(b), domes; (c) pyramids; (d)–(f) prepyramids. The Si
coverages are 0, 1, 2, 4, 8, and 16 ML’s for panels (a)–(f). From Rastelli et
al., 2001.
23. Формы островков Shape evolution
Геометрия островков InAs на GaAs и Ge на SiGeometry of InAs islands on GaAs and Ge on Si
Geometry of an InAs pyramid over
an InAs wetting layer deposited on
a GaAs(001) surface.
3D STM image (a) and schematic top and side views (b) of a 3D island formed during the deposition of
pure Ge on Si(001). All faces of the island are {105} facets. The height of the island is 2.8 nm while the
base dimensions are of the order of 20 and 40 nm. Due to frequently observed elongation of the islands—
that is either in [100] or [010] direction—the island’s shape resembles that of a “hut”. The vertical scale of
the STM image is exaggerated: the islands actually are fairly Kat with an 11.3° tilt angle of the facets as it is
shown in (b) (after Mo et al. and Teichert et al.).
24. Геометрия островков InAs на GaAs и Ge на Si Geometry of InAs islands on GaAs and Ge on Si
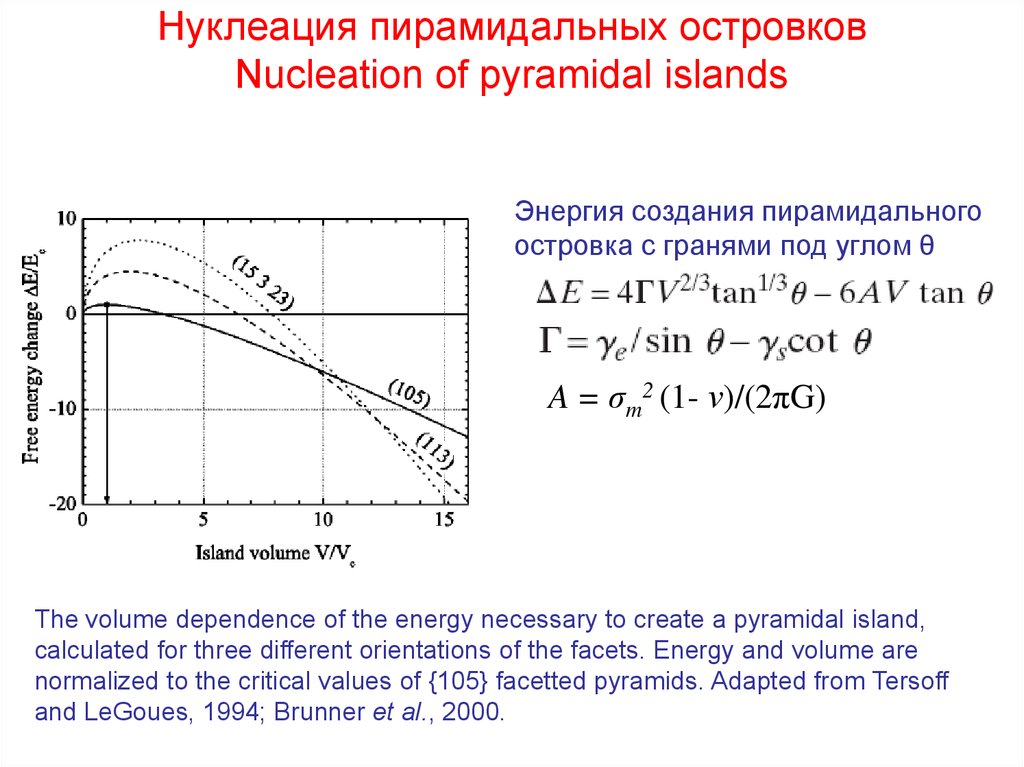
Нуклеация пирамидальных островковNucleation of pyramidal islands
Энергия создания пирамидального
островка с гранями под углом θ
A = σm2 (1- ν)/(2πG)
The volume dependence of the energy necessary to create a pyramidal island,
calculated for three different orientations of the facets. Energy and volume are
normalized to the critical values of {105} facetted pyramids. Adapted from Tersoff
and LeGoues, 1994; Brunner et al., 2000.
25. Нуклеация пирамидальных островков Nucleation of pyramidal islands
Фасетирование островков InAs на GaAsFacetting of InAs islands on GaAs
Facetting of InAs islands (a)
sketch of facets of an InAs
islands on GaAs(001)
obtained by STM; (b) and
(c) zoom of the
reconstructed {-1-37} facet;
(d) structure model of facet
reconstruction. From
Marquez et al., 2003.
26. Фасетирование островков InAs на GaAs Facetting of InAs islands on GaAs
Фасетирование островковFacetting of islands
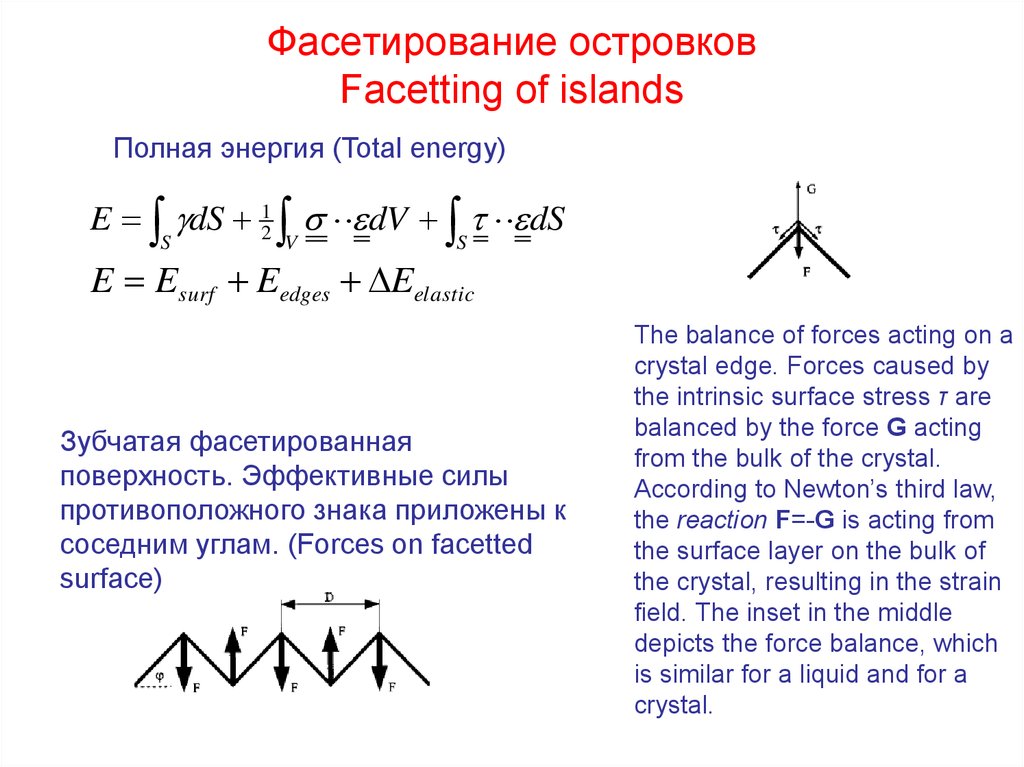
Полная энергия (Total energy)
E dS 12 dV dS
S
V
S
E Esurf Eedges Eelastic
Зубчатая фасетированная
поверхность. Эффективные силы
противоположного знака приложены к
соседним углам. (Forces on facetted
surface)
The balance of forces acting on a
crystal edge. Forces caused by
the intrinsic surface stress τ are
balanced by the force G acting
from the bulk of the crystal.
According to Newton’s third law,
the reaction F=-G is acting from
the surface layer on the bulk of
the crystal, resulting in the strain
field. The inset in the middle
depicts the force balance, which
is similar for a liquid and for a
crystal.
27. Фасетирование островков Facetting of islands
Энергия фасетированной поверхностиEnergy of facetted surface
Выигрыш в упругой энергии
Release of elastic energy
Полная энергия поверхности
Total energy of facetted surface
Оптимальный период
Optimal period
C ( ) m2 D
Eelastic
ln
ED
a
( ) ( ) C ( ) m2 D
E
ln
cos
D
ED
a
( ) E
Dopt a exp
1
~ 10a
2
C
(
)
m
The energy of a periodically faceted surface per unit surface area vs the
period D. There always exists an optimum period of faceting Dopt due to the
logarithmic dependence of the elastic relaxation energy on the period D.
28. Энергия фасетированной поверхности Energy of facetted surface
Самоорганизация QD на поверхности:Кинетика или термодинамика?
Self-organization: kinetics or thermodynamics?
• Формирование квантовых точек на поверхности
обычно проходит в неравновесных условиях
Formation happens under non-equilibrium conditions
• Термодинамические модели в целом описывают
наблюдаемые явления
Thermodynamics describes the process reasonably well
• Роль кинетики зависит от конкретной системы и
условий формирования квантовых точек
Role of kinetics is specific for systems and conditions
• Для большого числа практически важных
полупроводниковых гетеросистем разработаны
рецепты воспроизводимого получения массивов
квантовых точек на поверхности
Technology has been developed for reliable production
of quantum dots in different systems
29. Равновесность системы островков
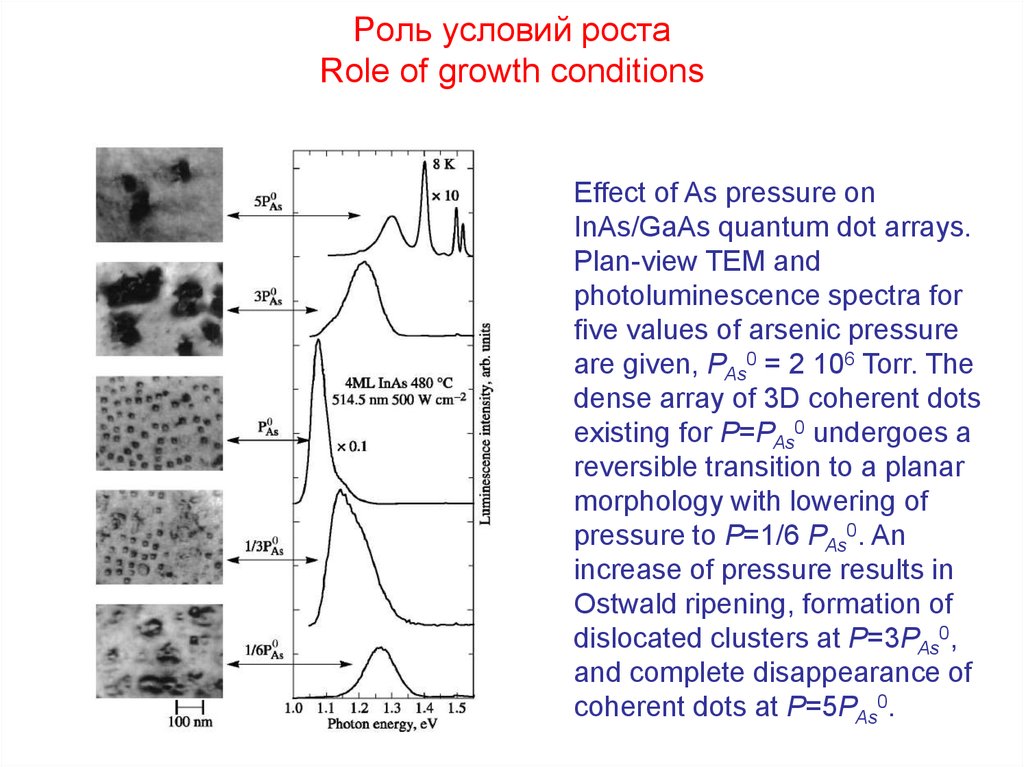
Роль условий ростаRole of growth conditions
Effect of As pressure on
InAs/GaAs quantum dot arrays.
Plan-view TEM and
photoluminescence spectra for
five values of arsenic pressure
are given, PAs0 = 2 106 Torr. The
dense array of 3D coherent dots
existing for P=PAs0 undergoes a
reversible transition to a planar
morphology with lowering of
pressure to P=1/6 PAs0. An
increase of pressure results in
Ostwald ripening, formation of
dislocated clusters at P=3PAs0,
and complete disappearance of
coherent dots at P=5PAs0.
30. Самоорганизация QD на поверхности: Кинетика или термодинамика? Self-organization: kinetics or thermodynamics?
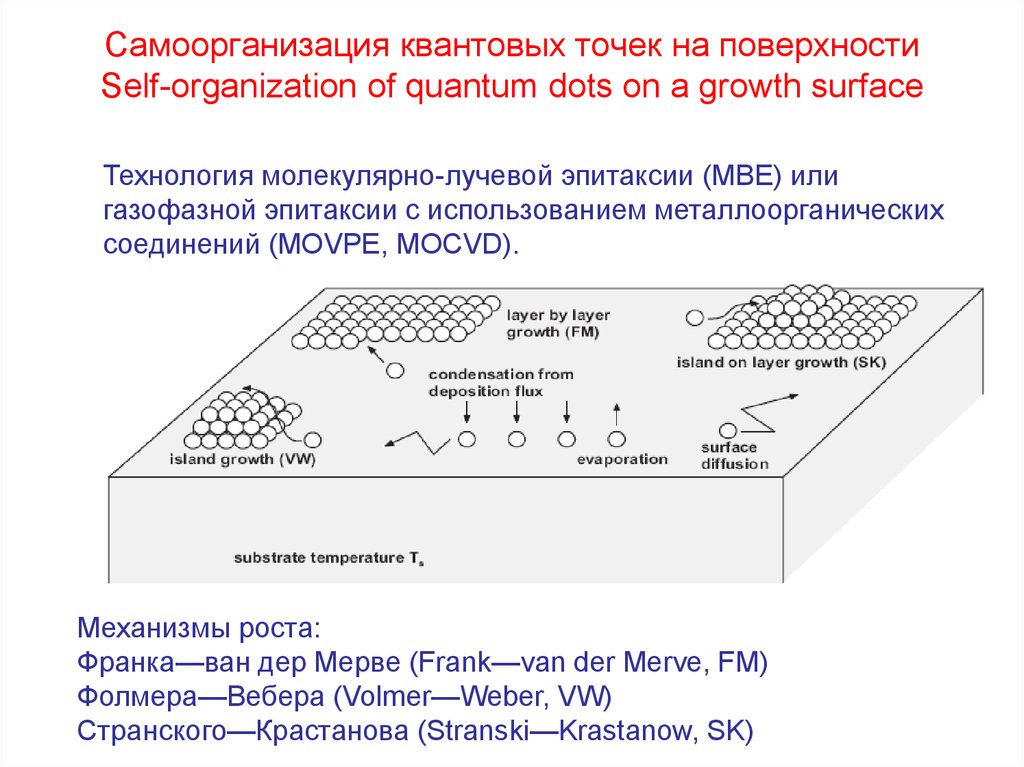
Самоорганизация квантовых точек на поверхностиSelf-organization of quantum dots on a growth surface
Технология молекулярно-лучевой эпитаксии (MBE) или
газофазной эпитаксии с использованием металлоорганических
соединений (MOVPE, MOCVD).
Механизмы роста:
Франка—ван дер Мерве (Frank—van der Merve, FM)
Фолмера—Вебера (Volmer—Weber, VW)
Странского—Крастанова (Stranski—Krastanow, SK)
31. Роль условий роста Role of growth conditions
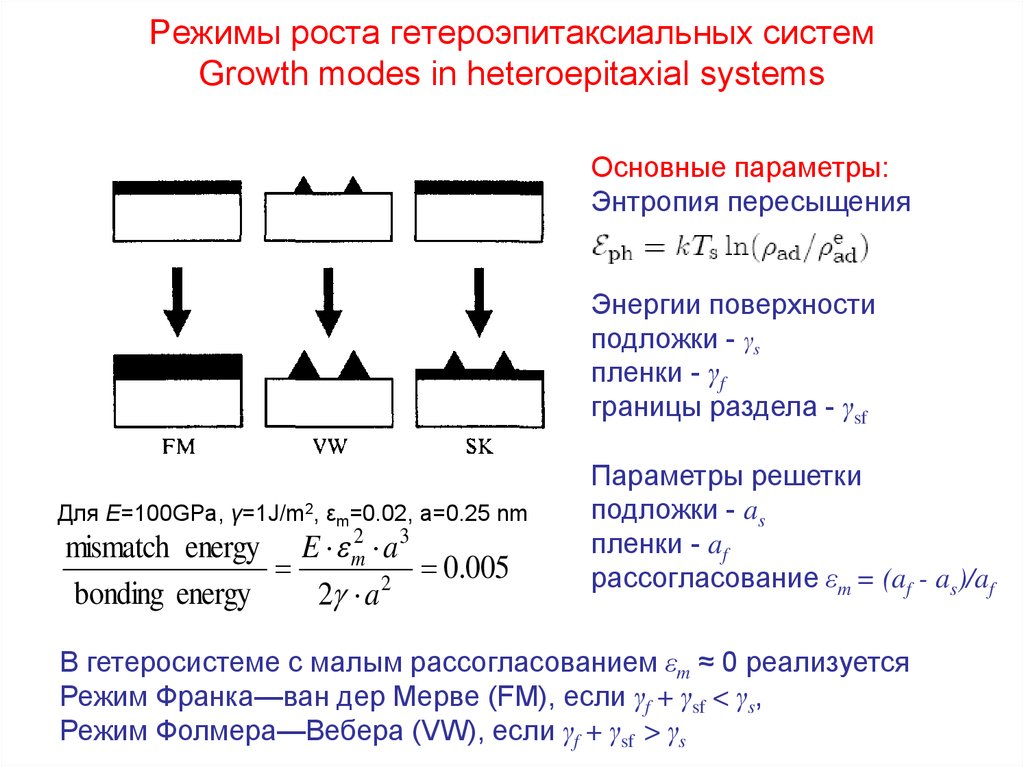
Режимы роста гетероэпитаксиальных системGrowth modes in heteroepitaxial systems
Основные параметры:
Энтропия пересыщения
Энергии поверхности
подложки - γs
пленки - γf
границы раздела - γsf
s
Для Е=100GPa, γ=1J/m2, εm=0.02, a=0.25 nm
mismatch energy E m2 a 3
0.005
2
bonding energy
2 a
Параметры решетки
подложки - as
пленки - af
рассогласование εm = (af - as)/af
В гетеросистеме с малым рассогласованием εm ≈ 0 реализуется
Режим Франка—ван дер Мерве (FM), если γf + γsf < γs,
Режим Фолмера—Вебера (VW), если γf + γsf > γs
32. Самоорганизация квантовых точек на поверхности Self-organization of quantum dots on a growth surface
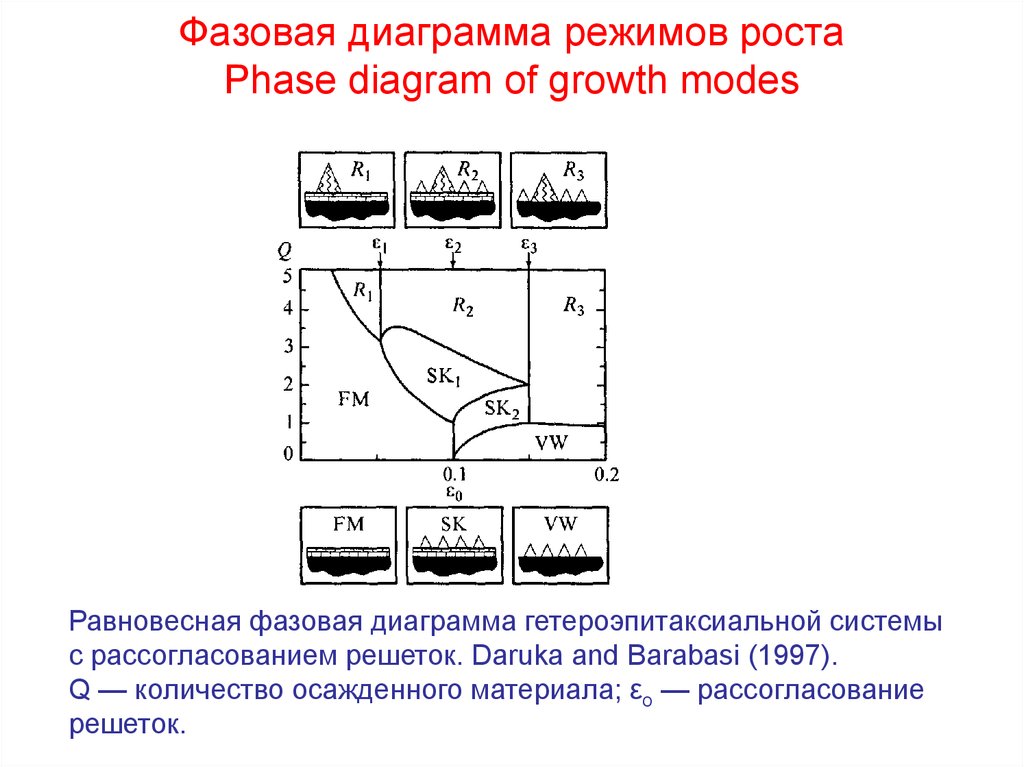
Фазовая диаграмма режимов ростаPhase diagram of growth modes
Равновесная фазовая диаграмма гетероэпитаксиальной системы
с рассогласованием решеток. Daruka and Barabasi (1997).
Q — количество осажденного материала; εо — рассогласование
решеток.
33. Режимы роста гетероэпитаксиальных систем Growth modes in heteroepitaxial systems
Домашнее задание (Homework) 5Пленка Ge толщиной 4 нм выращена
эпитаксиально на подложке Si с ориентацией (111)
и толщиной 400 мкм.
4-nm-thick Ge epitaxial film was grown over 400-μmthick Si substrate with (111) orientation.
Определить (determine)
4.2. Критическую длину Asaro-Tiller-Grinfeld
нестабильности пленки (γ = 1 J/m2).
Asaro-Tiller-Grinfeld critical length (γ = 1 J/m2).
5. Характерный размер квантовых точек Ge
Characteristic size of Ge quantum dots
34. Фазовая диаграмма режимов роста Phase diagram of growth modes
Латеральное упорядочение островковЭнергия латерального взаимодействия островков
R – расстояние между островками;
V – объем островка;
(mx ; my) – единичный вектор на поверхности;
B, C – константы;
для изотропной среды В2 = 0, изотропное дипольное
отталкивание;
для анизотропной среды возможно притяжение по “мягким”
направлениям, обычно <100>.
35. Домашнее задание (Homework) 5
Энергия латерального взаимодействияостровков на поверхности
Normalized interaction energy as a function of island separation, for islands with
aspect ratio AR = V/A3/2 = 1/3. Jonsdottir et al, 2006
36. Латеральное упорядочение островков
InAs на GaAsOrdering of quantum dots:
(a) plan-view transmission electron microscopy (TEM) micrograph
of a single sheet of InAs dots grown in molecular beam epitaxy by
four-monolayer deposition of InAs. Dots are preferentially aligned in
rows parallel to <100>.
(b) Histogram of the direction between the nearest neighboring dots.
37. Энергия латерального взаимодействия островков на поверхности
Искусственное упорядочение квантовых точекПроблемой самоорганизации КТ является статистический разброс размеров
Латеральное самоупорядочение КТ на поверхности малоэффективно
AFM images of the surface of a Ge layer grown on lithographically prepatterned
Si(001) substrates. In the sample shown at top left, the islands are arranged into
a regular array along two orthogonal <110> directions. In the sample shown at
bottom right, the unit vectors of the 2D array of pits are oriented along <100> and
<110> directions, leading to a 45° island alignment. Zhong and Bauer, 2004.
























 Физика
Физика








