Методы решения ЗЛП. Двойственность. Анализ оптимальных решений ЗЛП. (Леция 3)

1. Методы решения ЗЛП. Двойственность. Анализ оптимальных решений ЗЛП

Лекция
3
Add Your Company
Slogan
Методы решения ЗЛП.
Двойственность.
Анализ оптимальных
решений ЗЛП

2.

Свойства решений ЗЛП
.
1. Область
допустимых значений задачи линейного
программирования выпукла
2. Целевая функция ЗЛП достигает своего минимального
(максимального) значения в угловой точке многогранника
решений. Если целевая функция достигает своего
экстремального значения более чем в одной угловой
точке многогранника решений, то она достигает того же
значения в любой линейной выпуклой комбинации этих
угловых точек.
www.wondershare.com

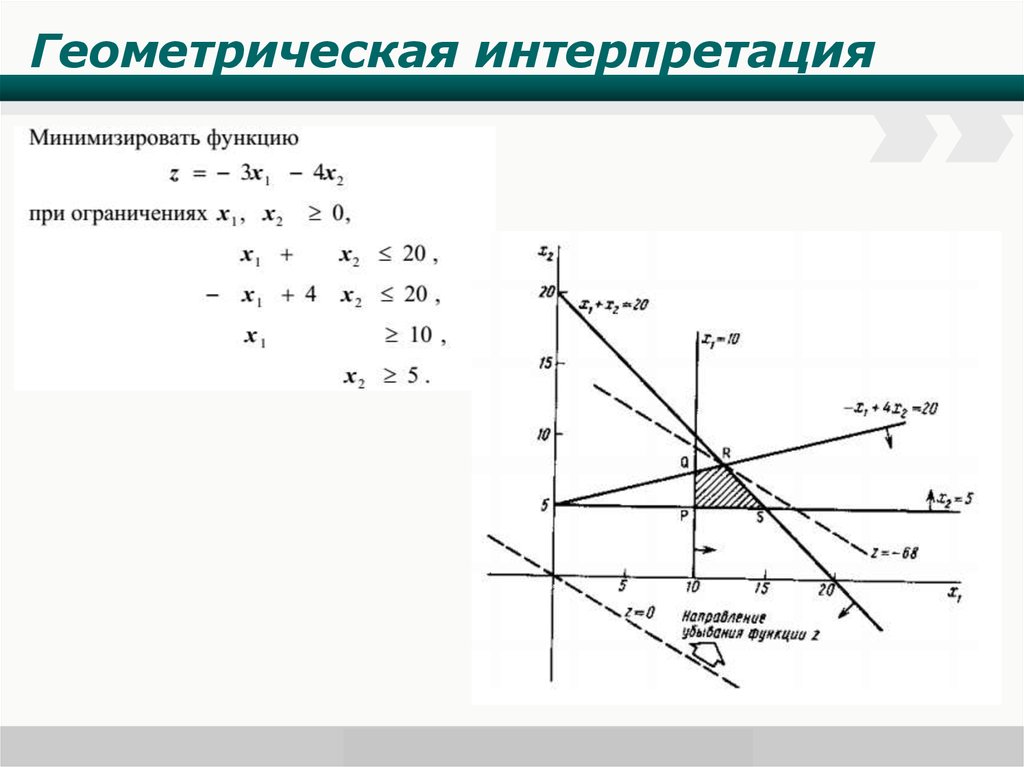
3. Геометрическая интерпретация

www.wondershare.com

4.

Симплекс-метод
www.wondershare.com

5.

Симплекс-метод
Методы контроля:
1. Z-оценки при базисных переменных равны нулю
2. Значения правой части всегда неотрицательны
3. Значение целевой функции на каждом шаге не
ухудшается.
Зацикливание
Зацикливание
может
возникать
при
наличии
вырожденного опорного решения. Выражается в том,
что значение целевой функции на следующем шаге не
меняется.
www.wondershare.com

6.

Исследование оптимальных решений
Исследование на устойчивость
Исследование на устойчивость – исследование диапазона
изменения правых частей системы ограничений, при котором
.
найденное
оптимальное решение не изменяется.
Исследование на чувствительность
При исследовании на чувствительность исследуется
зависимость решения ЗЛП от небольших изменений
коэффициентов в условии задачи. При этом предыдущее
решение
может
стать
либо
недопустимым,
либо
неоптимальным.
• К недопустимости пред. решения могут привести
изменения запасов ресурсов и/или добавление новых
ограничений.
• К неоптимальности пред. решения могут привести
изменение
целевой
функции
и/или
изменение
технологических коэффициентов и/или включение в модель
нового вида производственной деятельности.
www.wondershare.com

7.

Анализ решения ЗЛП
.
www.wondershare.com

8.

Анализ решения ЗЛП
.
www.wondershare.com

9.

Анализ решения ЗЛП
.
www.wondershare.com

10.

Графический анализ чувствительности
Изменение коэффициентов целевой функции
.
www.wondershare.com

11.

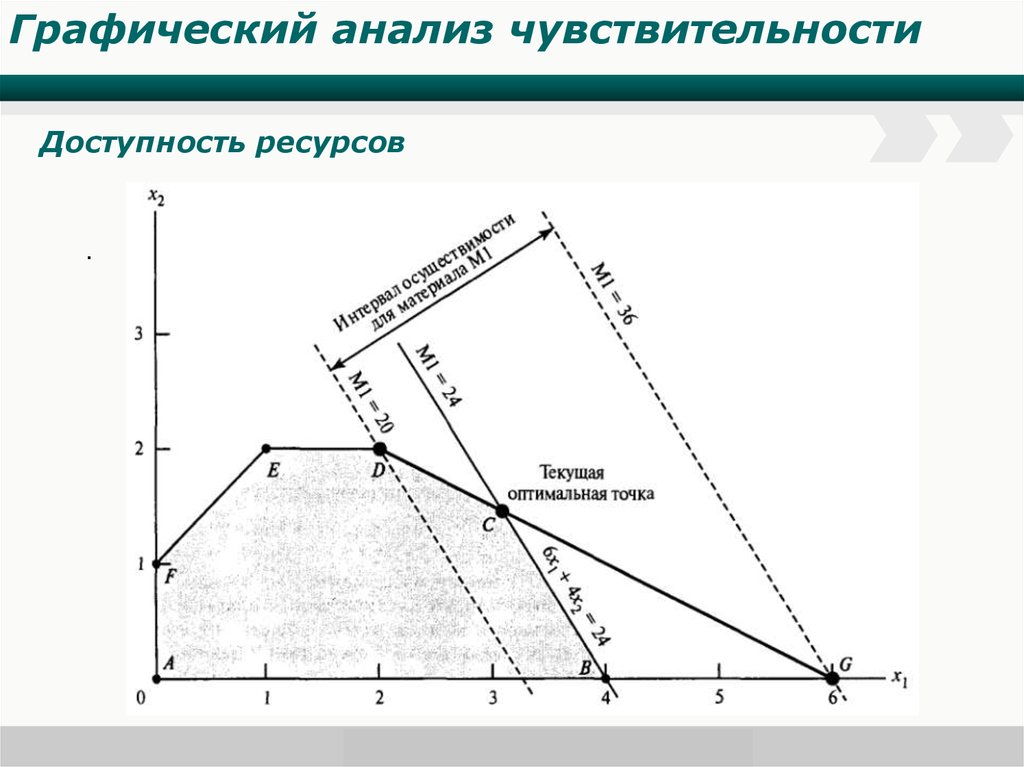
Графический анализ чувствительности
Доступность ресурсов
.
www.wondershare.com

12.

Графический анализ чувствительности
Доступность ресурсов
.
www.wondershare.com

13.

Двойственность в линейном программировании
Правила построения двойственных задач:
1. Если в исходной задаче целевая функция
исследуется на min, то в двойственной задаче она
будет исследоваться на max и наоборот.
2. Если в исходной задаче n переменных и m
уравнений, то в двойственной задаче будет m
переменных и n уравнений.
3.
Коэффициенты целевой функции исходной
задачи становятся правыми частями ограничений
двойственной задачи, а правые части системы
ограничений
исходной
задачи
становятся
коэффициентами целевой функции исходной задачи.
www.wondershare.com

14.

Двойственность в линейном программировании
4. Матрица
ограничений
двойственной
задачи получается из матрицы ограничений
исходной
задачи транспонированием.
.
xk 0,
то
в
5. Если в исходной задаче
двойственной
задаче
k-ое
ограничение
будет
неравенством, если же в исходной задаче x k не имело
ограничений на знак, то k-ое ограничение в
двойственной задаче будет равенством.
6. Если в исходной задаче l-ое ограничение неравенство, то в двойственной задаче y 0 ; если
l
же в исходной задаче l-ое ограничение - равенство, то
в двойственной задаче нет ограничений на знак yi.
www.wondershare.com

15.

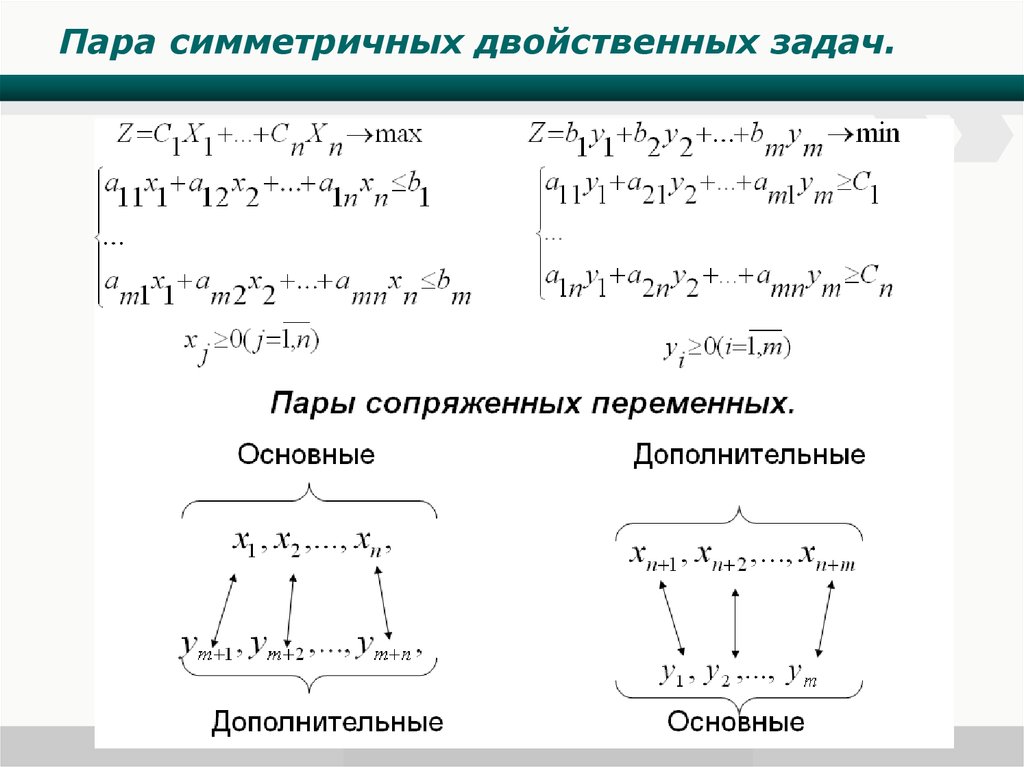
Пара симметричных двойственных задач.
www.wondershare.com

16.

Экономический смысл двойственности
.
www.wondershare.com

17.

Исследование на чувствительность
.
www.wondershare.com

18.

Экономический смысл двойственности
F 2 x1 3 x2 max
Z 18 y1 16 y2
x1 3 x2 18
2 x x 16
1 2
x2 5
3 x1 21
x1 , x2 0
F
*
5 y3 21 y4 min
y1 2 y2 3 y4 2
3 y1 y2 y3 3
y1 , y2 , y3 , y4 0
max
Z
*
min
24
www.wondershare.com

19.

Экономический смысл двойственности
Задача 1
Остатки ресурсов (ед.)
Число единиц
продукции
x*1 = 6 x*2 = 4 x*3 = 0
x*4 = 0 x*5 = 1 x*6 = 3
y*5 = 0 y*6 = 0 y*1 = 4/5 y*2 = 3/5 y*3 = 0 y*4 = 0
Превышение
Условные цены ресурсов
затрат на
ресурсы над
ценой
реализации
Задача 2
Компоненты оптимального решения двойственной задачи
называются оптимальными двойственными оценками исходной
задачи (скрытые доходы).
Они определяют степень дефицитности ресурса.
www.wondershare.com

20.

Метод искусственного базиса
Z 3x 2 x min
1
2
5 x 3x 5,
1
2
3x 10 x 10.
2
1
5 3
5
3 10
10
x ,x 0
1 2
Z 3x 2 x Mx Mx min
1
2
3
4
5 x 3x x 5,
1
2 3
3x 10 x x 10.
1
2 4
5 3 1 0 5
3 10 0 1 10
x ,x ,x ,x 0
1 2 3 4
www.wondershare.com

21.

Метод искусственного базиса
В результате может быть:
1. Получено оптимальное решение, в котором все
искусственные переменные равны нулю. Это и есть
оптимальное решение задачи.
2. Получено оптимальное решение, в котором хотя бы
одна искусственная переменная осталась в базисе.
Это означает, что исходная задача не имеет решения,
т.е. ОДЗ пустая.
3. В искусственной задаче видно, что целевая функция
не ограничена на ОДЗ.
www.wondershare.com