Методы оптимизации технических объектов. (Тема 3)

1.

2
ОСНОВЫ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
Занятие 3
МЕТОДЫ ОПТИМИЗАЦИИ ТЕХНИЧЕСКИХ ОБЪЕКТОВ
3.1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Одним из типовых приёмов системного анализа является представление исследуемого объекта в виде кибернетической системы, называемой «чёрным ящиком»:
Входные параметры,
характеризующие
воздействие на объект,
принято называть
факторами
Параметры, характеризующие реакцию объекта
на изменения факторов,
принято называть
откликами
Если речь идёт о технических объектах, факторами являются проектные
параметры объекта, которые мы можем изменять, стремясь улучшить качество
объекта: размеры, конфигурацию и взаимное расположение деталей, свойства
конструкционных материалов и рабочих сред, режимные параметры и т.п.).
В качестве откликов мы будем рассматривать функциональные параметры,
характеризующие качество выполнения объектом заданного назначения.
Эти показатели называют критериями оптимизации.

2.

Если в процессе оптимизации предполагается изменять один из проектных
параметров объекта − задача называется однопараметрической оптимизацией.
Если изменяемых параметров два и более − задача многопараметрическая.
2
Если в процессе оптимизации предполагается улучшать один показатель качества
объекта − задача называется однокритериальной оптимизацией.
Если ставится задача параллельно улучшить несколько характеристик объекта −
задача многокритериальная.
3.2. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
Если задача однокритериальная, она формулируется следующим образом:
− найти такое сочетание значений варьируемых факторов (y1*, Y2*, . . . Yк*), которое
обеспечивает максимальное (или минимальное) значение критерия, т.е.
К→Кmax или К→Кmin
Выбор направления поиска оптимума зависит от физической природы критерия:
если это показатель, увеличение которого желательно (например, удельная мощность,
коэффициент полезного действия и т.п.), выбирается движение к максимуму, если
желательно уменьшение показателя (например, масса, стоимость, виброактивность), то
выбирается движение к минимуму.
Если задача многокритериальная, то точного математического решения она, как
правило, не имеет в связи с противоречивостью критериев. Речь может идти только о
поиске и обосновании компромиссного решения.

3.

2
3.3. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ФАКТОРАМ
• Факторы должны выражаться количественной мерой. Если фактор выражается
качественной мерой, необходимо специальное кодирование.
• Факторы должны быть управляемыми, т.е. значения факторов должны подчиняться
воле лица, выполняющего оптимизацию. Если все факторы являются
управляемыми - можно проводить активную оптимизацию.
• Факторы должны быть совместимыми – т.е. никакое из запланированных
сочетаний значений факторов не должно приводить к аварии объекта, опасности
для персонала, заражению окружающей среды и т.п., а также к физически
Последнеепараметров
указание требует
некоторых пояснений:
нереальным значениям
объекта.
Допустим, мы имеем дело с машиной, рабочий процесс которой осуществляется с
• Факторы должны быть независимы друг от друга.
помощью порции газа массой G, химический состав которого определяется
коэффициентом R. Можем ли мы добиваться улучшения характеристик машины
путём одновременного воздействия на 3 термодинамических параметра газа:
объём V, давление P и абсолютную температуру T?
Люди, не знакомые с основами термодинамики газов, могут ответить: почему бы
и нет? Но мы-то с Вами, разумеется, знаем об уравнении Менделеева-Клапейрона,
связывающего эти параметры:
P∙V = G∙R∙T
Из него следует, что задав два из указанной тройки параметров, третий мы получим
в строгом соответствие с этим уравнением, поэтому число произвольно варьируемых
факторов для этой порции газа не может быть больше двух.

4.

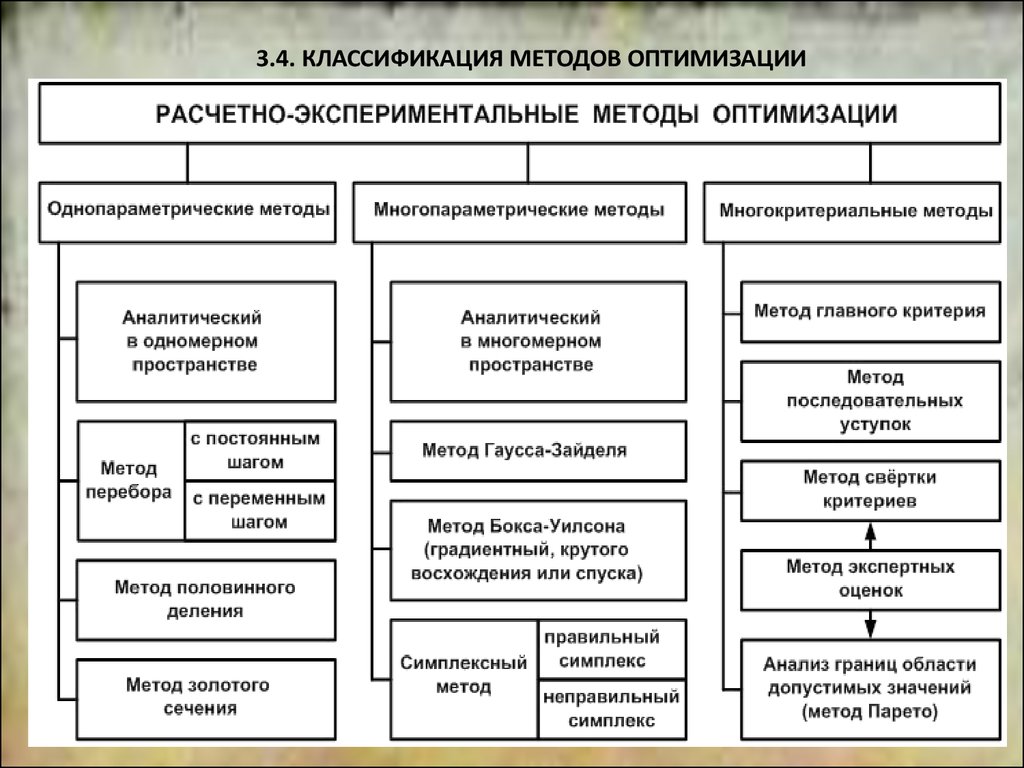
2
3.4. КЛАССИФИКАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ

5.

4. ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ
2
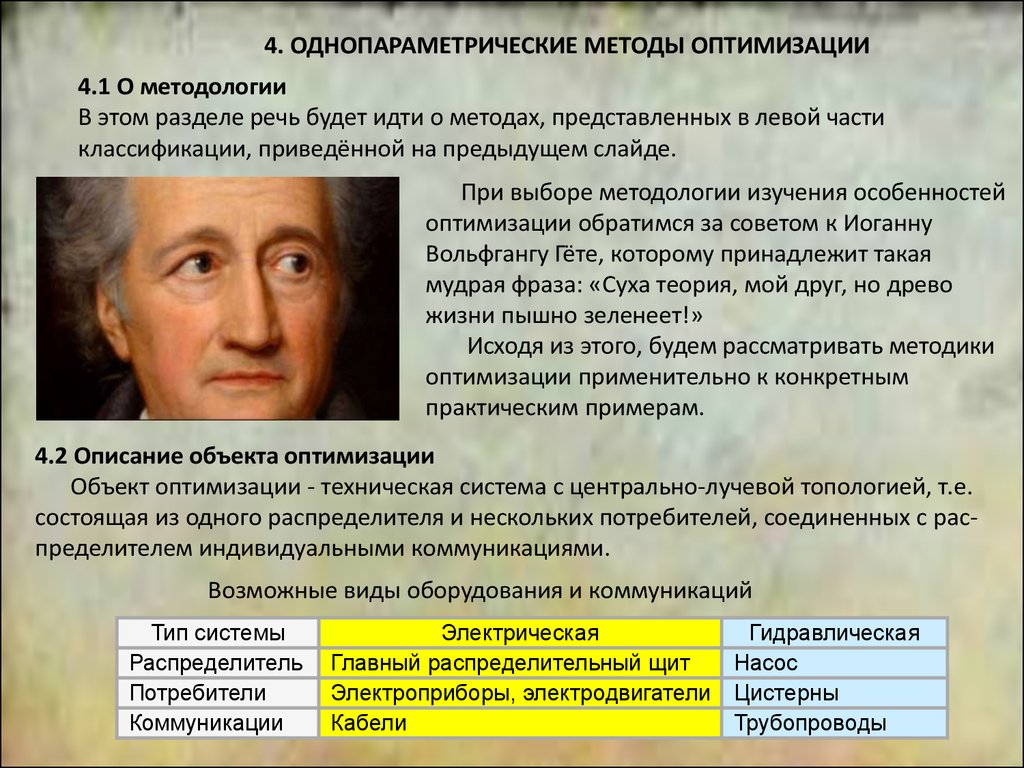
4.1 О методологии
В этом разделе речь будет идти о методах, представленных в левой части
классификации, приведённой на предыдущем слайде.
При выборе методологии изучения особенностей
оптимизации обратимся за советом к Иоганну
Вольфгангу Гёте, которому принадлежит такая
мудрая фраза: «Суха теория, мой друг, но древо
жизни пышно зеленеет!»
Исходя из этого, будем рассматривать методики
оптимизации применительно к конкретным
практическим примерам.
4.2 Описание объекта оптимизации
Объект оптимизации - техническая система с центрально-лучевой топологией, т.е.
состоящая из одного распределителя и нескольких потребителей, соединенных с распределителем индивидуальными коммуникациями.
Возможные виды оборудования и коммуникаций
Тип системы
Распределитель
Потребители
Коммуникации
Электрическая
Гидравлическая
Главный распределительный щит
Насос
Электроприборы, электродвигатели Цистерны
Кабели
Трубопроводы

6.

2
Потребители размещены в судовом пространстве или в производственном
помещении, имеющем форму параллелепипеда длиной L, шириной B и высотой H.
Коммуникации состоят из прямолинейных участков, параллельных продольной (X),
поперечной (Y) и вертикальной (Z) осям координат, и не имеют петель:
Условные обозначения:
Р – центральный распределитель;
П – потребители.
Габаритные размеры помещения:
длина L= 42 м; ширина B = 20 м; высота H =12 м
4.3 Формулировка цели оптимизации
№
1
2
3
4
5
6
7
8
9
Координаты потребителей и
характеристики коммуникаций:
удельные масса m и стоимость c
X(м) Y(м) Z(м) m(кг/м) c($/м)
4
1
11
3
8
7
3
11
6
10
16
5
1
10
15
20
7
1
5
10
30 13
6
10
15
35 15
6
12
20
37 19
8
15
30
40 10
7
15
30
41
6
7
10
25
Целью оптимизации является поиск наилучшего
расположения распределителя, при котором
минимальна суммарная длина коммуникаций
(критерий К1), суммарная масса коммуникаций
(критерий К2) или суммарная стоимость
коммуникаций (критерий К3).
Кроме того, может быть выполнена комплексная
оптимизация, учитывающая все три критерия.
Заданная точность оптимизации – 0,1 м
(по всем координатам).

7.

4.4 Возможности аналитического метода оптимизации
2
Как мы уже выяснили, оптимизация заключается в поиске условий, при которых
критерий оптимизации достигает экстремального (максимального или минимального)
значения.
Поиск координаты экстремума является вполне тривиальной математической задачей.
Её аналитическое решение заключается в том, что, если известна функция, описывающая
зависимость исследуемого критерия от варьируемого параметра К = f(X), нужно эту
функцию продифференцировать, приравнять производную нулю и,