Похожие презентации:
Бір факторлы және екі факторлы дисперсиялық талдау
1.
№ 19-20 ДәрісТақырыбы:
Бір факторлы және екі факторлы
дисперсиялық талдау.
2. Дәріс жоспары:
1.2.
3.
4.
5.
Дисперсиялық талдаудың негізгі түсініктері және
әдістері.
Жалпы, факторлық және қалдық дисперсиялар.
Бір факторлы дисперсиялық талдауды
қолданудың сызбасы.
Бір факторлы дисперсиялық талдаудың баламасы
Крускал-Уоллистің параметрлік емес белгісі.
Екі факторлы дисперсиялық талдау.
3. Дисперсиялық талдау
Дисперсиялықталдау деп
ағылшын
математигі
және
генетигі Р.Фишер ХХ ғасырдың
20-жылдарында биология мен
ауыл шаруашылығының бірқатар
эксперименттік тапсырмалары
үшін әзірленген статистикалық
әдістер топтамасын атайды.
Рональд Фишер
(1890—1962)
4.
Дисперсиялық талдаудағы есептіңқойылуы
Х1, Х2....Хk бас жинтықтары берілсін,
мұнда:
• барлық «k» таңдама қалыпты
үлестірілген;
• барлық таңдаманың дисперсиялары
бірдей.
Осындай шарттар орындалғанда және «р»
маңыздылық деңгейінде орташа шамалардың
теңдігінің нөлдік болжамын тексеру қажет, яғни
H0: x1 х2 ... хk .
5.
Дисперсиялық талдаудың негізгітүсініктері және әдістері
Бас жинтықтың кез келгеніне бір немесе бірнеше
факторлар әсер етіп, олардың орташа мәндерін
өзгертуі мүмкін.
Фактор - соңғы нәтижеге әсерін тигізетін көрсеткіш.
Фактор деңгейі - фактордың нақты іске асуы.
Жауап (үн қату) - өлшенетін белгінің мәні.
6.
Дисперсиялық талдаудың негізгітүсініктері және әдістері
1 мысал. Гипертония ауруына шалдыққан кейбір науқастар санына
қарай кездейсоқ түрде «k» топтарына бөлінген, олардың әрқайсысына
белгілі бір дәрі-дәрмек қабылдау тағайындалған. Нәтижесінде
артериалдық қысым көрсеткішінің орташа мәнінің өзгеруі бақылауға
алынады.
Бұл мысалда:
•дәрі-дәрмек – бұл бақылаудағы көрсеткіш шамасына ықпалын
тигізетін фактор;
•артериялық қысым өзгерісінің көрсеткіші – бұл фактор ықпалына
деген үн қату.
Топтар бойынша қабылданатын дәрідәрмектер не түрімен, не мөлшерімен, не
қандай да бір басқа жағдайларымен
ажыратылады деген болжам бар. Онда
ықпал етуші фактор, фактор деңгейлері
деп аталатын бірқатар құрамдарға бөлінеді.
7.
Дисперсиялық талдаудың негізгітүсініктері және әдістері
Егер фактор шаманың үн қатуына әсер етсе, онда шамалар
орташаларының теңдігі туралы H0: x1 х2 ... хk нөлдік
болжам қабылданбайды.
Зерттеліп отырған факторлар санына байланысты
дисперсиялық талдау бірфакторлы және көпфакторлы
болып бөленеді.
1 мысалдағы артериалдық қысымның өзгеруін зерттеу
жолдары:
• фактор – жыл маусымы (деңгейлері: қыс, көктем, жаз,
күз);
• фактор – тәжирібе жүргізілетін орын (оның деңгейлері:
ауруханада немесе үйде емделу);
• фактор – режим (оның деңгейлері: төсекте, әдеттегідей
немесе таза ауада үнемі жаяу жүру) және т.б.
8.
Дисперсиялық талдаудың негізгітүсініктері және әдістері
Бір факторлы дисперсиялық талдау үшін таңдалған деректерді
кесте түрінде жазады.
«А» факторының деңгейі
Сынақ нөмері
A1
A2
...
Ak
1
x11
x12
...
x1k
2
x21
x22
...
x2k
...
...
...
...
...
nj
xn11
x n2 2
...
x nk k
Топтық орташа
xтоп1
xтоп 2
...
xтопk
9. Дәріс жоспары:
1.2.
3.
4.
5.
Дисперсиялық талдаудың негізгі түсініктері және
әдістері.
Жалпы, факторлық және қалдық дисперсиялар.
Бір факторлы дисперсиялық талдауды
қолданудың сызбасы.
Бір факторлы дисперсиялық талдаудың баламасы
Крускал-Уоллистің параметрлік емес белгісі.
Екі факторлы дисперсиялық талдау.
10. Жалпы, факторлық және қалдық дисперсиялар
Дисперсиялық талдаудың негізгі мақсаты таңдамалыдисперсияны екі құрамдас бөлікке бөлу:
• біріншісі – бұл орташа мәндердің өзгеруіне әсерін тігізетін
факторге сәйкес келетін факторлық дисперсия;
• екіншісі – бұл кездейсоқ себептер әсерінен пайда болатын,
орташалардың өзгеріуіне әсерін тигізетін қалдық
дисперсия.
Зерттелетін факторды сандық жағынан бағалау үшін осы
құрамдас бөліктерді Фишер F-белгісімен салыстыру
қолданылады.
11. Факторлық дисперсия (S2факт ) – бұл фактордың әсерінен таңдаманың орташа шамаларының өзгеруіне сәйкес келетін дисперсия:
Жалпы, факторлық және қалдықдисперсиялар
Факторлық дисперсия (S2факт ) – бұл фактордың әсерінен
таңдаманың орташа шамаларының өзгеруіне сәйкес келетін
дисперсия:
k
S
мұндағы
SS факт
2
факт
SS факт
k 1
r x топ j x
2
j 1
k 1
- орташа квадраттық ауытқулардын факторлық
қосындысы,
k - фактор деңгейлерінің саны,
r - әр топтағы мәндер саны,
х - жалпы орташа,
х топ - топтық орташа.
12.
Жалпы, факторлық және қалдық дисперсияларS 2 ќалд
Қалдық дисперсия (
) – бұл орташа шамалардың өзгеруіне
ықпал етпейтін, кездейсоқ себептер әсерінен ғана болатын
дисперсия:
r
r
r
S
2
ќалд
SS ќалд
x
i 1
i1
x топ1 xi 2 x топ 2 ... xi k x топ k
2
2
i 1
2
i 1
,
k (r 1)
k (r 1)
мұндағы SS ќалд - ауытқулар квадраттарының қалдық
қосындысы.
Жалпы дисперсия – бұл
дисперсияның қосындысы:
факторлық
SS жалпы SS факт SS калд.
және
қалдық
13. Дәріс жоспары:
1.2.
3.
4.
5.
Дисперсиялық талдаудың негізгі түсініктері және
әдістері.
Жалпы, факторлық және қалдық дисперсиялар.
Бір факторлы дисперсиялық талдауды
қолданудың сызбасы.
Бір факторлы дисперсиялық талдаудың баламасы
Крускал-Уоллистің параметрлік емес белгісі.
Көп факторлы дисперсиялық талдау.
14. Бір факторлық дисперсиялық талдауды жүргізу сызбасы
.Бір факторлық дисперсиялық
талдауды жүргізу сызбасы
1) Н0: x1 х2 ... хk .
Н1: x1 x2 ... хk .
2) р=0,05 – маңыздылық деңгейі.
3) Fесеп
S 2 факт
2
.
S ќалд
4) F
кесте ( р; f1 ; f 2 ),
мұндағы f1=k-1, f2=k(r-1) – еркіндік дәрежелер саны,
k - фактор деңгейінің саны, r - әр топтағы мәндер саны.
5) Егер Fесеп ≤ Fкесте болса, онда «H0» қабылданады.
Егер Fесеп > Fкесте болса, онда «H0» қабылданбайды.
15. Бір факторлы дисперсиялық талдауды қолдану мысалы
2 мысал. Белгілі бір жас санатындағы ересек тұрғындар арасында екіжыл бойындағы тыныс алу жолдары ауруларының саны тіркелген.
Кездейсоқ түрде әрқайсысы 4 адамнан тұратын 3 топ іріктеліп алынды,
олардың ішінде:
1 топ – темекі тартпайтындар,
2 топ – темекі тарту өтелі 5 жылға дейін,
3 топ – темекі тарту өтелі 5 жылдан астам.
хij – 12 ауру санының мәні алынды, мұндағы j – фактор деңгейінің
нөмірі (j=1,2,3), i – топтағы нөмірі (i=1,2,3,4):
x11
x
21
x31
x41
x12 x13
1
0
x22 x23
1
x32 x33
x42 x43
2
3 3
2 4
.
2 5
1 3
Темекі тартудың тыныс алу жолдары ауруларына
тігізетін әсері маңызды ма екендігін анықтау керек.
16. Бір факторлы дисперсиялық талдауды қолдану мысалы
2 мысал.Шешуі.
«А» факторы – темекі тарту,
фактор деңгейлері А1, А2, А3 - темекі тарту өтелі,
факторына жауап - тыныс алу жолдарының ауру саны.
xij - қалыпты үлестірілген жинақтан алынған таңдама деп
қарастырылады. Барлық берілгендерді кестеге енгізу керек:
Сынақ нөмері
«А» факторының деңгейі
A1
A2
A3
1
1
3
3
2
0
2
4
3
1
2
5
4
2
1
3
Топтық орташа
4/4=1
8/4=2
15/4=3,75
17. Бір факторлы дисперсиялық талдауды қолдану мысалы
2 мысал.Шешуі (жалғасы).
1) Н0: x1 х2 ... хk .
Н1: x1 x2 ... хk .
2) р=0,05 – маңыздылық деңгейі.
3) Есептеледі:
3.1) Жалпы орташа:
х1 х2 х3 1 2 3,75
х
2,25.
3
3
3.2) Квадраттық ауытқудың факторлық қосындысы:
3
SS факт r x топ j x
2
j 1
4 1 2,25 2 2,25 3,75 2,25 15,5.
2
2
2
18. Бір факторлы дисперсиялық талдауды қолдану мысалы
2 мысал.Шешуі (жалғасы).
3.3) Факторлық дисперсия:
SSфакт 15,5
2
Sфакт
7,75.
k 1 3 1
3.4) Квадраттық ауытқудың қалдық қосындысы:
4
4
4
SS ќалд xi1 x топ1 xi 2 x топ 2 xi k x топ 3
i 1
2
2
i 1
2
i 1
(1 1) 2 (0 1) 2 (1 1) 2 (2 1) 2 (3 2) 2 (2 2) 2 (2 2) 2 (1 2) 2
(3 3,75) 2 (4 3,75) 2 (5 3,75) 2 (3 3,75) 2 6,75.
19. Бір факторлы дисперсиялық талдауды қолдану мысалы
2 мысал.Шешуі (жалғасы).
3.5) Қалдық дисперсия:
SS ќалд
6,75
2
S ќалд
0,75.
k (r 1) 3(4 1)
3.6) Fесеп
4)
5)
S 2 факт 7,75
2
10,3.
S ќалд 0,75
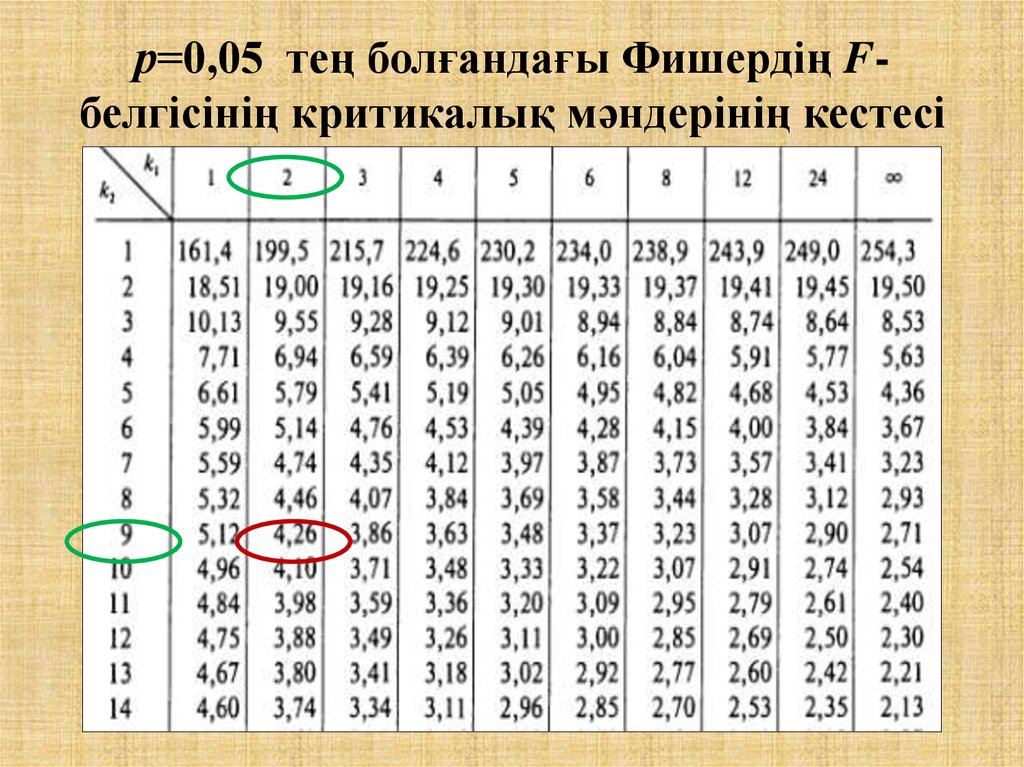
Fкесте (0,05; 2; 9)=4,26.
Fесеп > Fкесте болса, онда «H0» қабылданбайды, яғни темекі
тарту факторы тыныс алу жолдары ауруларына елеулі әсерін
тигізеді.
20. р=0,05 тең болғандағы Фишердің F-белгісінің критикалық мәндерінің кестесі
р=0,05 тең болғандағы Фишердің Fбелгісінің критикалық мәндерінің кестесі21. Дәріс жоспары:
1.2.
3.
4.
5.
Дисперсиялық талдаудың негізгі түсініктері және
әдістері.
Жалпы, факторлық және қалдық дисперсиялар.
Бір факторлы дисперсиялық талдауды
қолданудың сызбасы.
Бір факторлы дисперсиялық талдаудың баламасы
Крускал-Уоллистің параметрлік емес белгісі.
Екі факторлы дисперсиялық талдау.
22. Крускал-Уоллистің параметрлік емес белгісі
Крускал–Уоллис Н-белгісі - үш және одан көп тәуелсізтоптарды салыстыру үшін дисперсиялық талдаудың параметрлік
емес баламасы.
М. Крускал
(1925—2006)
У. Уоллис
(1912—1998)
Аталған белгі берілгендердің нақты берілген мәндері емес,
олардың шендерін қолданып есептейді.
Егер топтағы үлестірім бір қалыпты болмаса, Н-белгісі
қолданылады.
23. Крускал-Уоллистің параметрлік емес белгісі
Үштаңдаманы
салыстырғанда,
олардың
әрқайсысында 3 бақылаудан кем болмауы,
немесе 4 бақылаудан, ал басқасында - 2-ден; бұл
жерде қай таңдамада қанша сынақ жүргізілгені
емес, олардың 4:2:2 қатынасы маңызды.
Н-белгісінің критикалық мәндері таңдаманың
саны k≤5, ал сынақтың саны әрбір топта ni≤8
болған жағдайда ғана қарастырылады.
Үлкен көлемді таңдама санында және әрбір
таңдамадағы сынақта кестеден χ2-белгісінің
критикалық мәнін қолдануға болады.
24.
Крускал – Уоллистің Н-белгісінқолданудың сызбасы
1) Н0:
Н1:
x1 х2 ... хk .
x1 x2 ... хk .
2) р=0,05 – маңызыдылық деңгейі.
3)
k
Ri2
12
3 n 1 ,
n n 1 i 1 ni
Н есеп
k
мұндағы n ni - барлық топ бойынша жалпы бақылау саны,
i 1
Ri - i-ші таңдама шендерінің қосындысы.
4) Егер k≤5 болса, онда Н кесте (р;n1;n2;…;n5), мұндағы n1;n2;…;n5
– қарастырылатын таңдаманың көлемдері.
2
Егер k>5 болса, онда Н кесте кесте ( р; f ) , мұндағы f=k-1 –
еркіндік дәреежелерінің саны.
5) Егер Н есеп < Н кесте болса, онда «H0» қабылданады.
Егер Н есеп ≥ Н кесте болса, онда «H0» қабылданбайды.
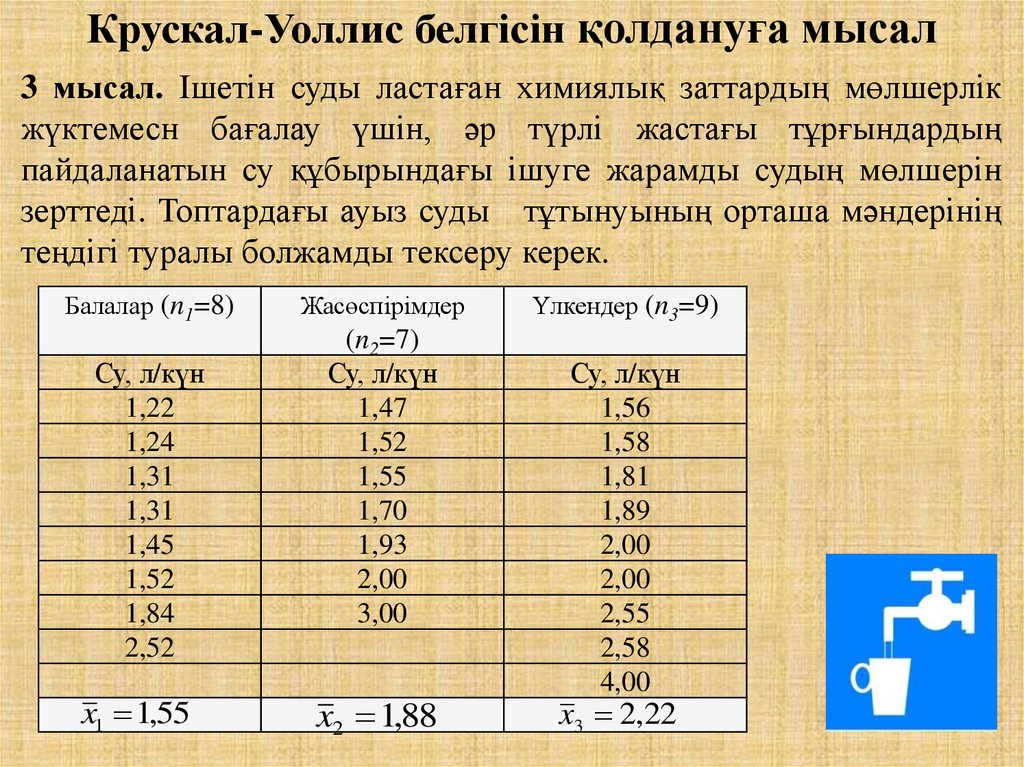
25. Крускал-Уоллис белгісін қолдануға мысал
3 мысал. Ішетін суды ластаған химиялық заттардың мөлшерлікжүктемесн бағалау үшін, әр түрлі жастағы тұрғындардың
пайдаланатын су құбырындағы ішуге жарамды судың мөлшерін
зерттеді. Топтардағы ауыз суды тұтынуының орташа мәндерінің
теңдігі туралы болжамды тексеру керек.
Балалар (n1=8)
Су, л/күн
1,22
1,24
1,31
1,31
1,45
1,52
1,84
2,52
x1 1,55
Жасөспірімдер
(n2=7)
Су, л/күн
1,47
1,52
1,55
1,70
1,93
2,00
3,00
x2 1,88
Үлкендер (n3=9)
Су, л/күн
1,56
1,58
1,81
1,89
2,00
2,00
2,55
2,58
4,00
x3 2,22
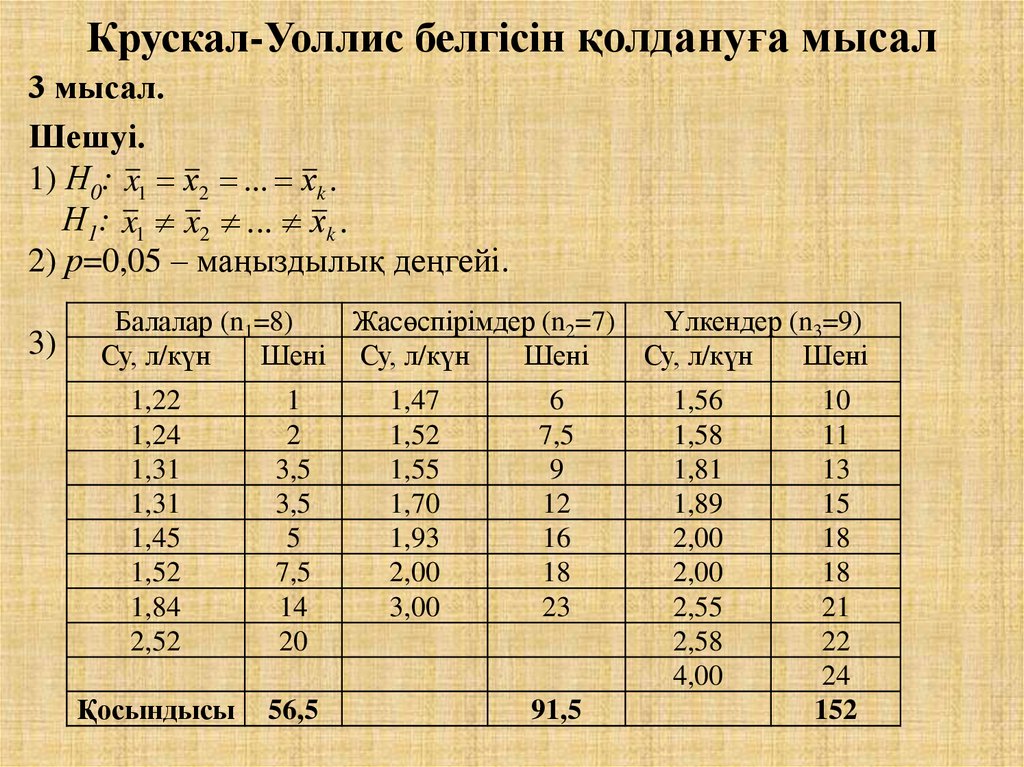
26. Крускал-Уоллис белгісін қолдануға мысал
3 мысал.Шешуі.
1) Н0: x1 х2 ... хk .
Н1: x1 x2 ... хk .
2) р=0,05 – маңыздылық деңгейі.
3)
Балалар (n1=8)
Жасөспірімдер (n2=7)
Үлкендер (n3=9)
Су, л/күн
Шені Су, л/күн
Шені
Су, л/күн
Шені
1,22
1,24
1,31
1,31
1,45
1,52
1,84
2,52
1
2
3,5
3,5
5
7,5
14
20
Қосындысы
56,5
1,47
1,52
1,55
1,70
1,93
2,00
3,00
6
7,5
9
12
16
18
23
91,5
1,56
1,58
1,81
1,89
2,00
2,00
2,55
2,58
4,00
10
11
13
15
18
18
21
22
24
152
27. Крускал-Уоллис белгісін қолдануға мысал
3 мысал.Шешуі (жалғасы).
Н есеп
k
Ri2
12
3 n 1
n n 1 i 1 ni
56,52 91,52 152 2
12
3 (24 1)
24 (24 1) 8
7
9
0,02 (399 1196 2567,1) 75 8,24.
2
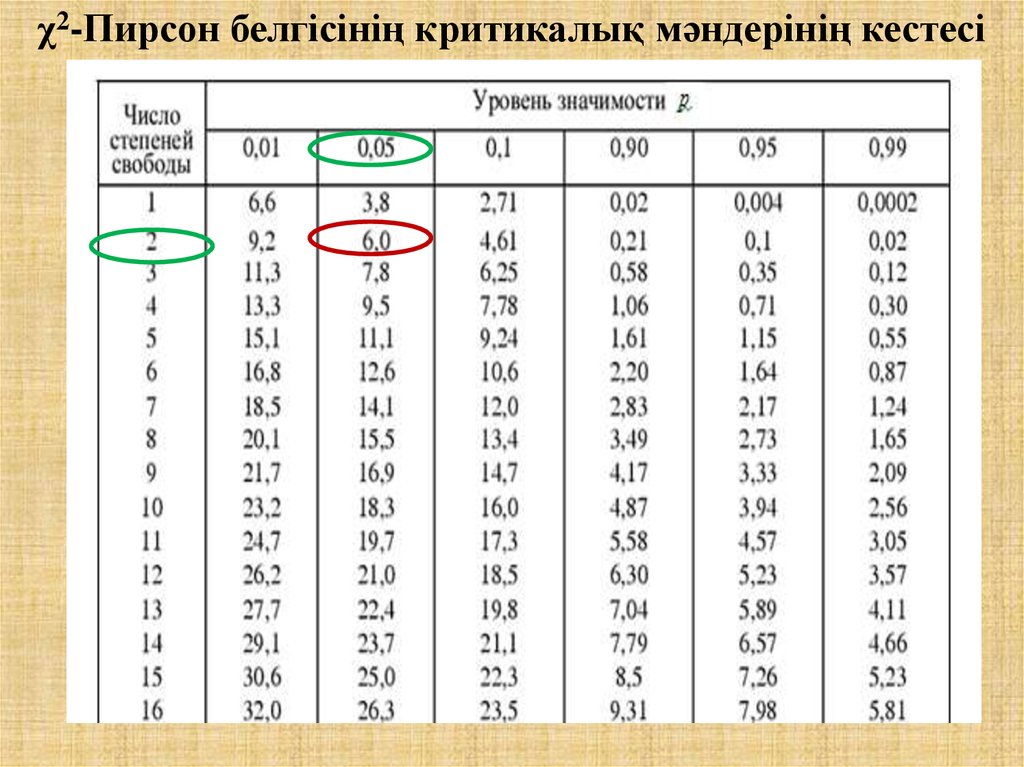
4) Н кесте кесте
(0,05; 2) 6.
5) Н есеп Н кесте болса, онда «H0» қабылданбайды,
яғни әр түрлі жастағы топтарда күнделікті әр
түрлі мөлшерде ішетін су пайдаланылады.
28. χ2-Пирсон белгісінің критикалық мәндерінің кестесі
29. Дәріс жоспары:
1.2.
3.
4.
5.
Дисперсиялық талдаудың негізгі түсініктері және
әдістері.
Жалпы, факторлық және қалдық дисперсиялар.
Бір факторлы дисперсиялық талдауды
қолданудың сызбасы.
Бір факторлы дисперсиялық талдаудың баламасы
Крускал-Уоллистің параметрлік емес белгісі.
Екі факторлы дисперсиялық талдау.
30.
Екі факторлы дисперсиялық талдауЕкі факторлы дисперсиялық талдау – белгіге екі
ұйымдастырылған
фактор
әсер
етуін
зерттейтін
статистикалық әдістер жүйесі.
Екі факторлық дисперсиялық талдау тек әр фактордың жеке
әсерін ғана емес, сонымен қатар олардың өзара
әрекеттесуінің де әсерін бағалауға мүмкіндік береді.
Екі факторлы дисперсиялық талдауды үлкен болғандықтан,
оны есептеу үшін арнайы бағдарламаларды («Statistica 10»,
SPSS және т.б.) пайдалануды ұсынады.
31.
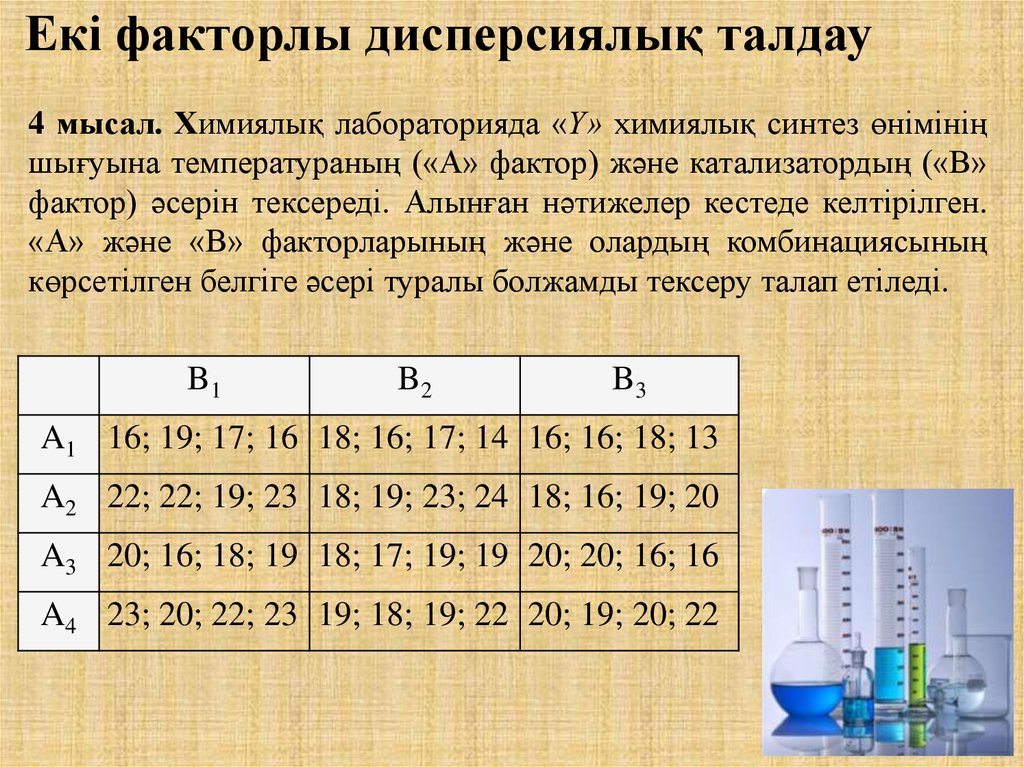
Екі факторлы дисперсиялық талдау4 мысал. Химиялық лабораторияда «Y» химиялық синтез өнімінің
шығуына температураның («А» фактор) және катализатордың («В»
фактор) әсерін тексереді. Алынған нәтижелер кестеде келтірілген.
«А» және «В» факторларының және олардың комбинациясының
көрсетілген белгіге әсері туралы болжамды тексеру талап етіледі.
B1
B2
B3
A1 16; 19; 17; 16 18; 16; 17; 14 16; 16; 18; 13
A2 22; 22; 19; 23 18; 19; 23; 24 18; 16; 19; 20
A3 20; 16; 18; 19 18; 17; 19; 19 20; 20; 16; 16
A4 23; 20; 22; 23 19; 18; 19; 22 20; 19; 20; 22
32.
Екі факторлы дисперсиялық талдау4 мысал. Шешуі.
1) Болжамды құрастыру.
«A» факторы үшін болжам:
Н0: «Ai» температураның барлық режимінде «Y» химиялық синтез
өнімінің нәтижелерінің орташалары арасында айырмашылық жоқ.
Н1: «Ai» температураның барлық режимінде «Y» нәтижелерінің
орташалары арасында айырмашылық бар.
«B» факторы үшін болжам:
Н0: «Bj» катализатор түрлері үшін «Y» орташа нәтижелері арасында
айырмашылық жоқ.
Н1: «Bj» катализатор түрлері үшін «Y» орташа нәтижелері арасында
айырмашылық бар.
«А» және «В» факторларының өзара әсерлері үшін
болжам:
Н0: «А» және «В» факторлары «Y» нәтижесіне тиімді
өзара әсері болмайды.
Н1: «А» және «В» факторлары «Y» нәтижесіне тиімді
өзара әсері болады.
33.
Екі факторлы дисперсиялық талдау4 мысал.
Шешуі (жалғасы).
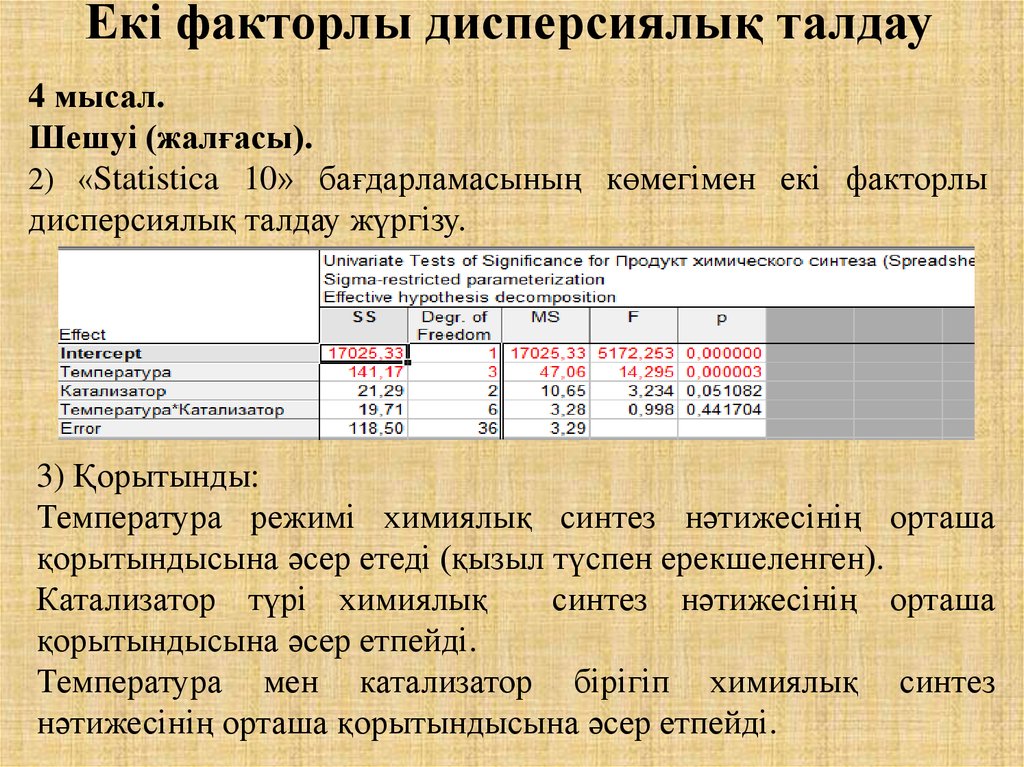
2) «Statistica 10» бағдарламасының көмегімен екі факторлы
дисперсиялық талдау жүргізу.
3) Қорытынды:
Температура режимі химиялық синтез нәтижесінің орташа
қорытындысына әсер етеді (қызыл түспен ерекшеленген).
Катализатор түрі химиялық
синтез нәтижесінің орташа
қорытындысына әсер етпейді.
Температура мен катализатор бірігіп химиялық синтез
нәтижесінің орташа қорытындысына әсер етпейді.
34. Бақылау сұрақтары:
1. Қандай нөлдік болжам дисперсиялықталдаудың көмегімен тексеріледі?
2. Дисперсиялық талдауды қолданғанда
қандай шарттар орындалуы керек?
3. Дисперсиялық талдаудың негізгі
идеясы қандай?
4. Крускал–Уоллистің Н-белгісі қай кезде
қолданылады?




























 Математика
Математика








