Похожие презентации:
Биостатистика. Сапалы белгілерді талдау
1.
БИОСТАТИСТИКА№ 16-17 Дәріс
Сапалы белгілерді талдау.
2. Дәріс жоспары
1. Түйіндес кестелер.2. Екі тәуелсіз популяцияның пропорциясын
салыстыру. Пирсонның χ2- келісім белгісі.
3. Йетс түзетуі.
4. Екі тәуелді популяцияның пропорциясын
салыстыру. Макнемардың χ2- белгісі.
3.
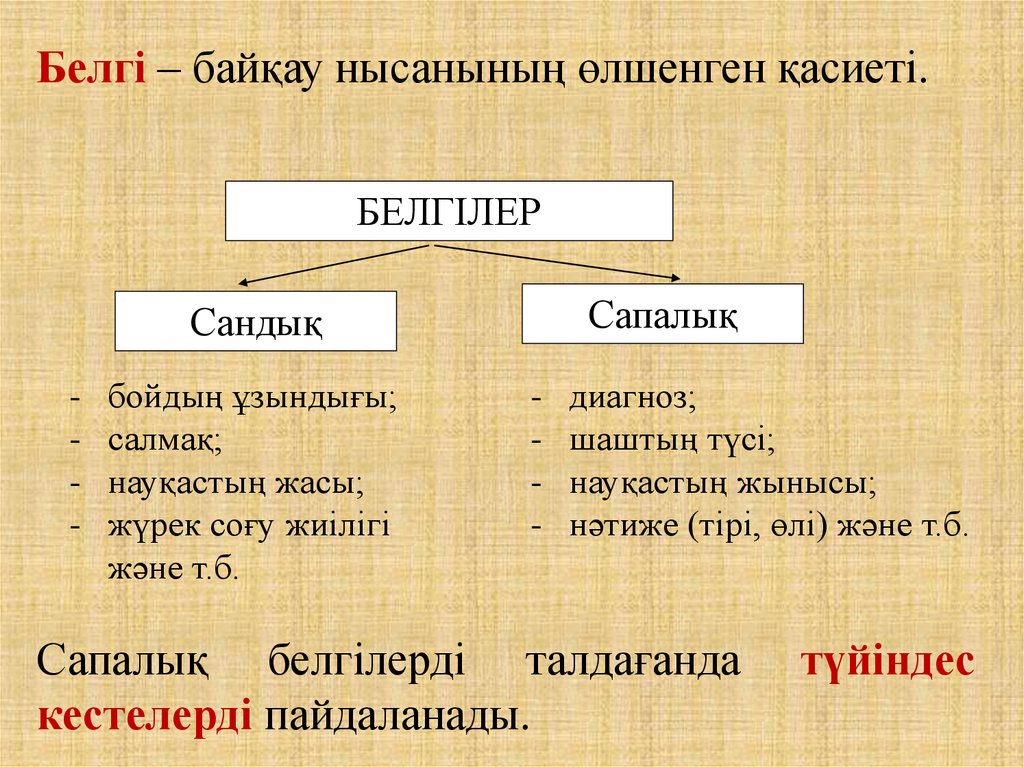
Белгі – байқау нысанының өлшенген қасиеті.БЕЛГІЛЕР
Сапалық
Сандық
-
бойдың ұзындығы;
салмақ;
науқастың жасы;
жүрек соғу жиілігі
және т.б.
-
диагноз;
шаштың түсі;
науқастың жынысы;
нәтиже (тірі, өлі) және т.б.
Сапалық белгілерді талдағанда
кестелерді пайдаланады.
түйіндес
4. Түйіндес кестелер
Екі «А» және «В» сапалы белгілері болсын. «А»белгісінің сатылары (градация) - r, ал «B» белгісінің
сатылары - s.
Көлемі n таңдама берілген.
Таңдаманың
әрбір
нысаны
«А»
белгісінің
деңгейілерінің біреуіне және бір мезгілде қандайда бір
«В» белгісінің деңгейіне ие болуы мүмкін. Осы таңдама
арқылы Аi және Вj оқиғаларының жиіліктерін жеке
және кез келген комбинацияда анықтауға болады.
5.
Түйіндес кестелерАiBj. Оқиғасының жиілігі νij белгіленген.
белгісінің пайда болу саны (Аi белгісінің жиілігі)
s
i. ij i1 i 2 ... is
j 1
тең болады.
Bj белгісінің пайда болу саны
r
. j ij 1 j 2 j ... rj
i 1
тең болады.
Жалпы бақылау саны, яғни таңдама көлемі:
r
s
i 1
j 1
r
s
.. i. . j ij
i 1 j 1
Аi
6.
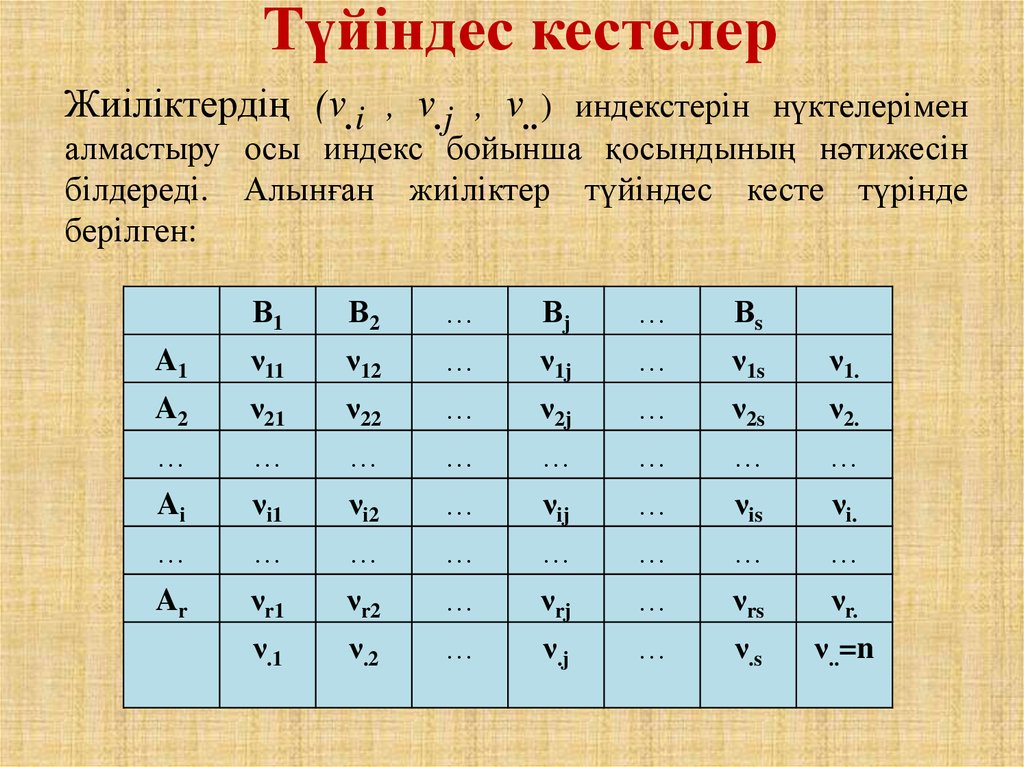
Түйіндес кестелерЖиіліктердің (ν.i , ν.j , ν..) индекстерін нүктелерімен
алмастыру осы индекс бойынша қосындының нәтижесін
білдереді. Алынған жиіліктер түйіндес кесте түрінде
берілген:
В1
В2
…
Вj
…
Вs
A1
ν11
ν12
…
ν1j
…
ν1s
ν1.
A2
ν21
ν22
…
ν2j
…
ν2s
ν2.
…
…
…
…
…
…
…
…
Ai
νi1
νi2
…
νij
…
νis
νi.
…
…
…
…
…
…
…
…
Ar
νr1
νr2
…
νrj
…
νrs
νr.
ν.1
ν.2
…
ν.j
…
ν.s
ν..=n
7.
Түйіндес кестелерТүйіндес кестелерді талдау кезінде нөлдік болжам
келесі түрде беріледі:
Н0: А және В белгілер арасында байланыс жоқ.
8.
Түйіндес кестелерТүйіндес кестенің әрбір ұяшығы үшін теориялық жиіліктер
есептеледі (яғни АiBj комбинацияларының әрқайсына).
. j
.i
..
*
ij
В1
В2
A2
11*
*
21
12*
*
22
…
…
…
A1
Ai
i*1
i*2
…
…
…
Ar
*
r1
*
r2
.*1=
.*2 =
ν.1
ν.2
…
Вj
…
1*j
2* j
…
…
…
…
ij*
…
…*
…
…
rj
.*j =
ν.j
…
Вs
…
1s* 1*. = ν
1.
*
*
2 s 2=. ν
2.
…
…
…
…
is*
…
…
…
…
*
rs
.s* =
ν.s
…
i*. = ν
*
r.
i.
…
= νr.
ν..
9.
Түйіндес кестелерН0 болжамы орындалған кезде бақыланатын νij
жиіліктері ij* теориялық жиілітерінен
айырмашылығы көп болмау керек.
Теориялық және бақыланатын жиіліктерді
салыстыру
үшін
Пирсонның
χ2-белгісі
қолданылады.
10. Дәріс жоспары
1. Түйіндес кестелер.2. Екі тәуелсіз популяцияның пропорциясын
салыстыру. Пирсонның χ2- келісім белгісі.
3. Йетс түзетуі.
4. Екі тәуелді популяцияның пропорциясын
салыстыру. Макнемардің χ2- белгісі
11. Пирсонның χ2 - белгісі
Бұл белгі, егер түйіндес кестесініңұяшықтарында жиіліктер 5-тен жоғары
немесе
тең
болғанда
сапалық
сипаттамаларды
талдау
үшін
қолданылады.
Егер байқау саны аз болса және кесте
торындағы ұяшықтардың жиілігі 5-тен аз
болса,
онда
χ2
өлшемі
белгісі
қолданылмайды.
Оның
орнына
Фишердің нақты белгісі қолданылады.
12.
Пирсонның χ2 – келісім белгісінқолданудың тізбесі
1) Н0: белгілердің арасында байланыс жоқ.
Н1: белгілердің арасында байланыс бар.
2) р=0,05 – маңызыдылық деңгейі
3)
r
2
есеп
s
i 1 j 1
ij
*
ij
* 2
ij
,
мүндағы νij – бақыланатын жиіліктер, ν*ij – теориялық
жиіліктер
2
4)
кесте ( р, f ) , мұндағы f =(r-1)(s-1) - еркіндік дәреже
саны (2 қосымшаны қара).
2
2
5) Егер есеп < кесте болса, онда «H0» қабылданады.
2
2
есеп > кесте болса, онда «H » қабылданбайды.
Егер
0
13.
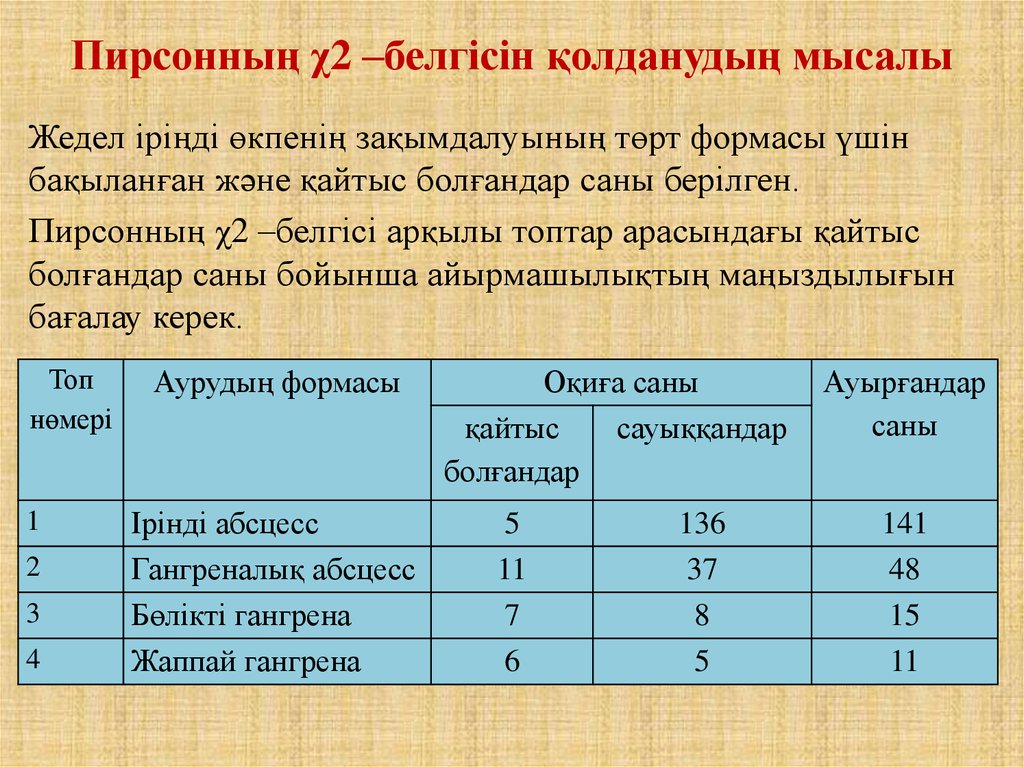
Пирсонның χ2 –белгісін қолданудың мысалыЖедел іріңді өкпенің зақымдалуының төрт формасы үшін
бақыланған және қайтыс болғандар саны берілген.
Пирсонның χ2 –белгісі арқылы топтар арасындағы қайтыс
болғандар саны бойынша айырмашылықтың маңыздылығын
бағалау керек.
Топ
нөмері
1
2
3
4
Аурудың формасы
Ірінді абсцесс
Гангреналық абсцесс
Бөлікті гангрена
Жаппай гангрена
Оқиға саны
қайтыс
сауыққандар
болғандар
5
11
7
6
136
37
8
5
Ауырғандар
саны
141
48
15
11
14.
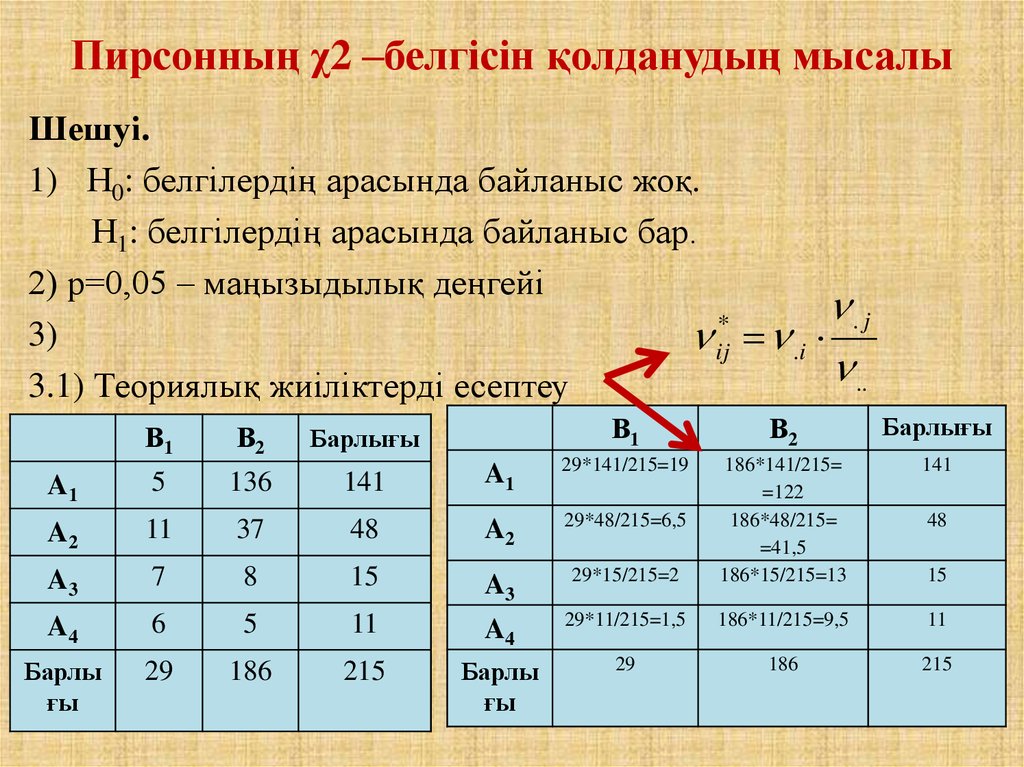
Пирсонның χ2 –белгісін қолданудың мысалыШешуі.
1) Н0: белгілердің арасында байланыс жоқ.
Н1: белгілердің арасында байланыс бар.
2) р=0,05 – маңызыдылық деңгейі
. j
*
3)
ij .i
..
3.1) Теориялық жиіліктерді есептеу
В1
В2
Барлығы
В1
В2
Барлығы
29*141/215=19
141
A1
5
136
141
A1
A2
11
37
48
A2
29*48/215=6,5
A3
7
8
15
A3
29*15/215=2
186*141/215=
=122
186*48/215=
=41,5
186*15/215=13
A4
6
5
11
A4
29*11/215=1,5
186*11/215=9,5
11
Барлы
ғы
29
186
215
Барлы
ғы
29
186
215
48
15
15.
Пирсонның χ2 –белгісін қолданудың мысалыШешуі (жалғасы).
3.2) Шамасын есептеу
ij
* 2
ij
*
ij
В1
В2
A1
(5-19)2/19=10,3
(136-122)2/122=1,6
A2
(11-6,5)2/6,5=3,1
(37-41,5)2/41,5=0,5
A3
(7-2)2/2=12,5
(8-13)2/13=1,9
A4
(6-1,5)2/1,5=13,5
(5-9,5)2/9,5=2,1
3.3) Есеп
r
s
2
есеп
i 1 j 1
*
ij
ij
*
ij
2
10,3 3,1 12,5 13,5 1,6 0,5 2 2,1 45,5
16.
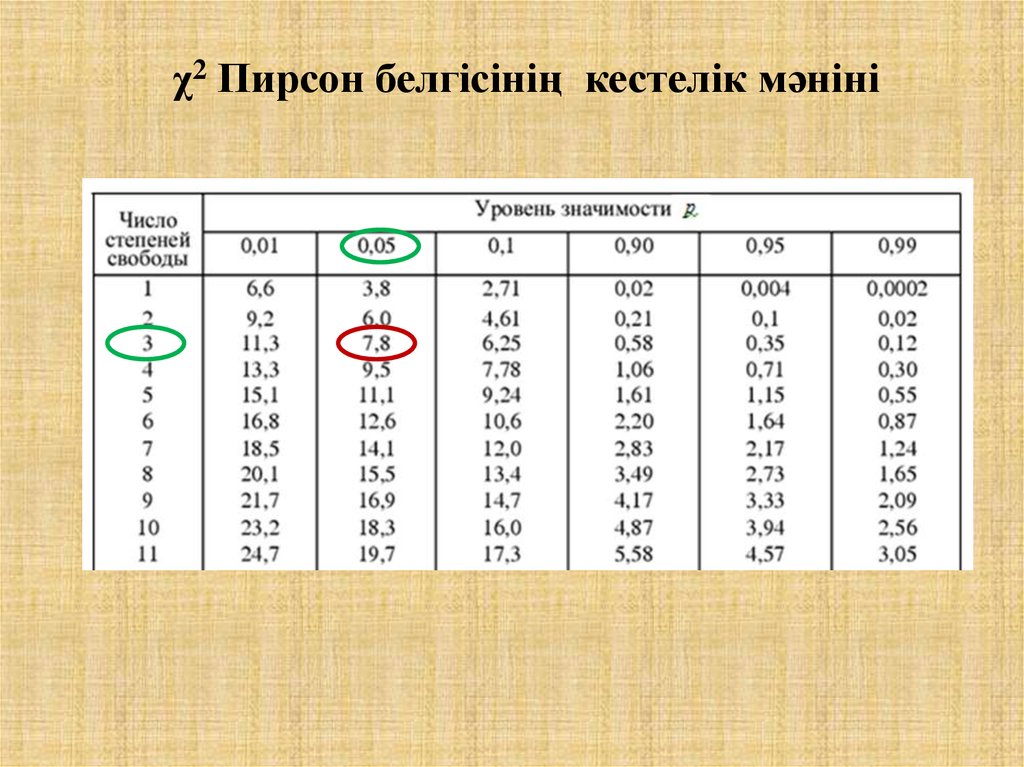
Пирсонның χ2 –белгісін қолданудың мысалыШешуі (жалғасы).
2
4) кесте ( р, f ) , мұндағы f =(r-1)(s-1) =(4-1)(2-1)=3 –
еркіндік дәрежісі саны, (қосымша 2 қара).
2
кесте
(0,05;3) 7,8
2
2
есеп
5) Егер
> кесте болса, онда «H0» қабылданбайды,
яғни топтар арасындағы қайтыс болғандар саны бойынша
айырмашылық маңызды.
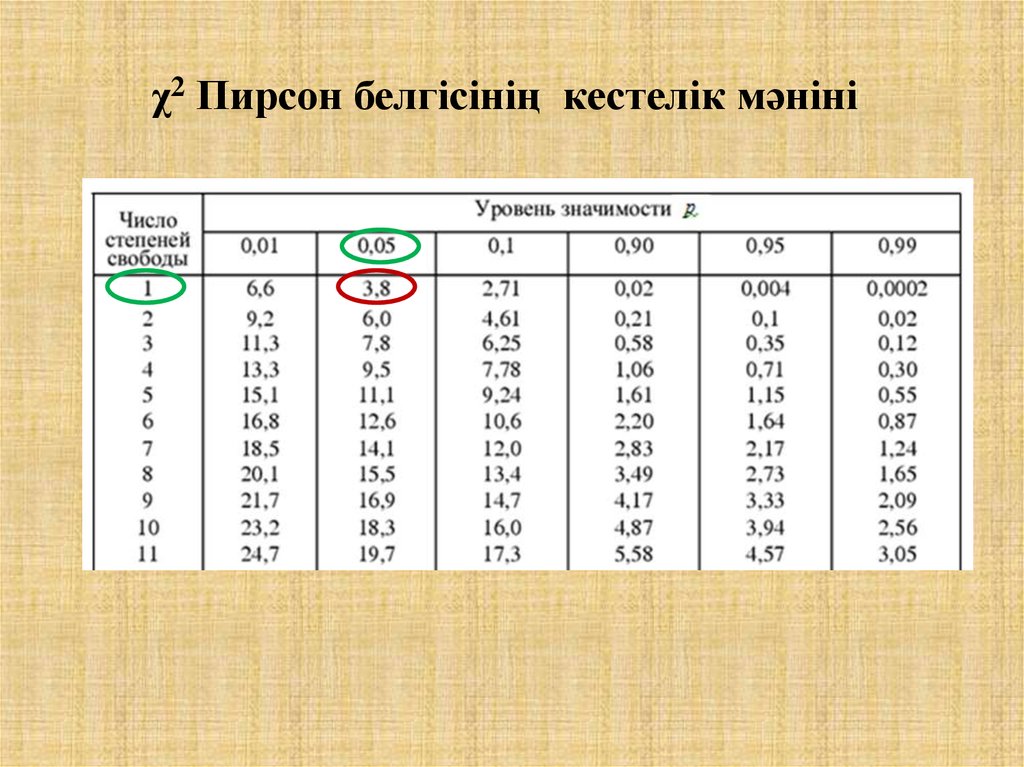
17.
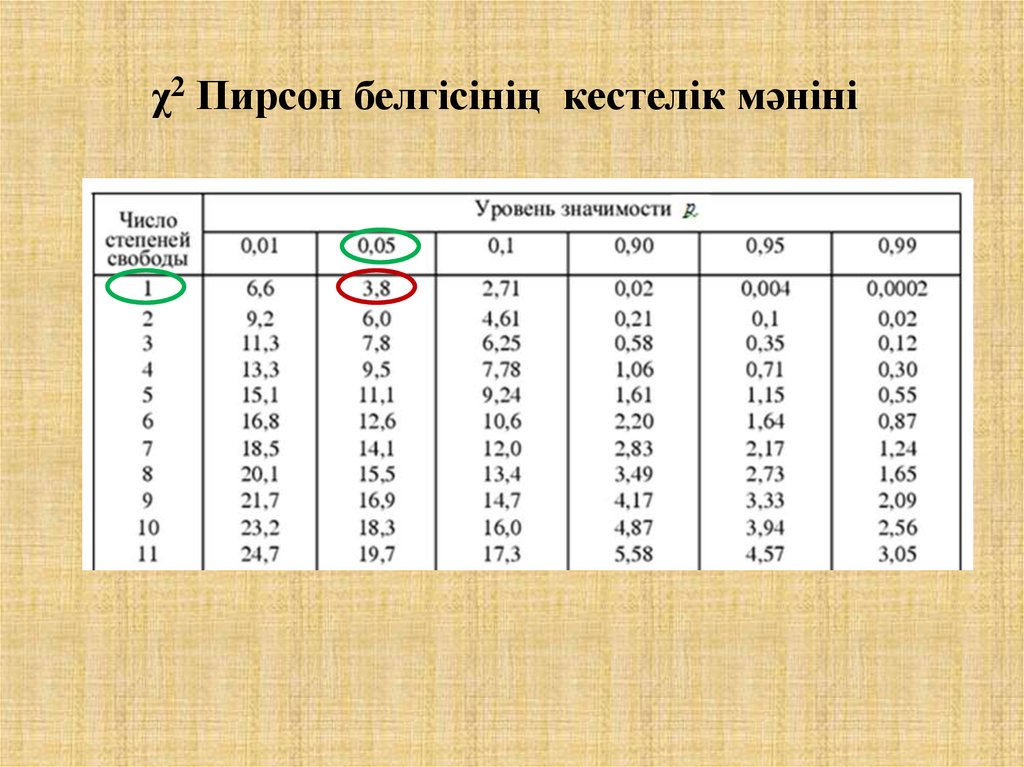
χ2 Пирсон белгісінің кестелік мәніні18.
Белгіні есептеу рәсімі өте күрделі, сондықтанталдауды арнайы (мысалы, «STATISTICA»)
бағдарламасы арқылы орындау тиімді.
19. «STATISTICA» бағдарламасында Пирсонның χ2 – белгісін орындаудың мысалы
1. Деректерді енгізу.2. «Basic statistics and
tables» модулі,
«Tables and banners»
рәсімі. Түйіндес
кесте құру.
3. «Expected
frequencies»,
«Pearson & M-L
Chi-square»
опциялары.
4. Қорытынды кесте.
1
2
4
Р<0,05 болғандықтан болжам
қабылданбайды, яғни белгілер
арасында байланыс бар.
3
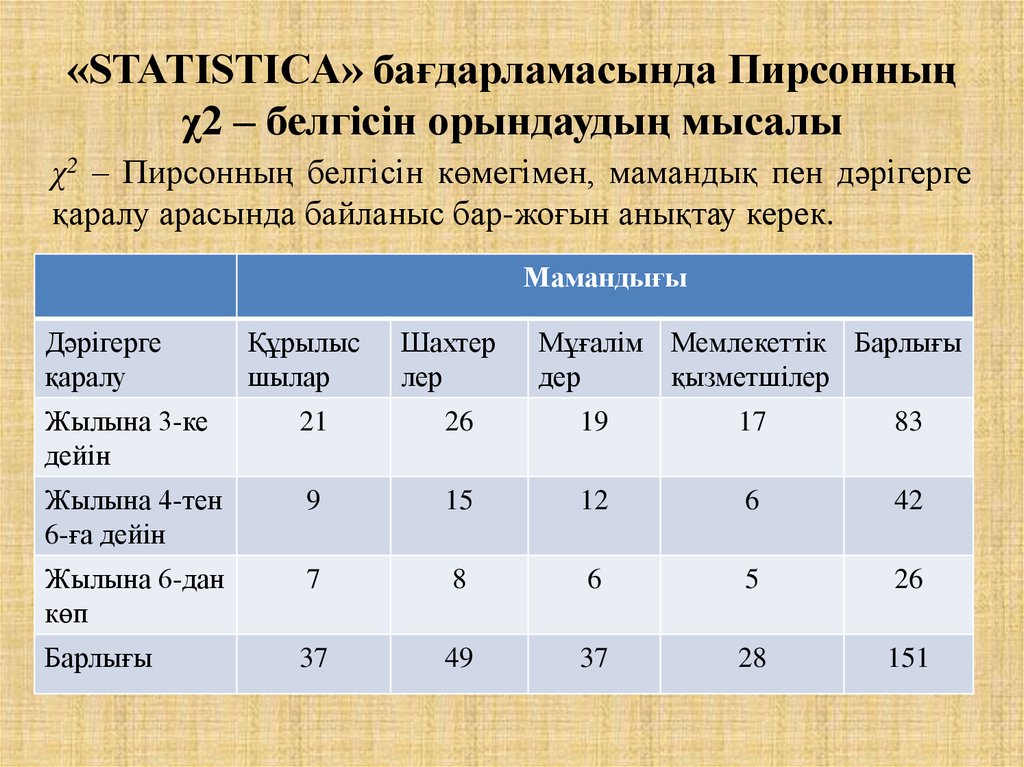
20. «STATISTICA» бағдарламасында Пирсонның χ2 – белгісін орындаудың мысалы
χ2 – Пирсонның белгісін көмегімен, мамандық пен дәрігергеқаралу арасында байланыс бар-жоғын анықтау керек.
Мамандығы
Дәрігерге
қаралу
Құрылыс
шылар
Шахтер
лер
Мұғалім Мемлекеттік Барлығы
дер
қызметшілер
Жылына 3-ке
дейін
21
26
19
17
83
Жылына 4-тен
6-ға дейін
9
15
12
6
42
Жылына 6-дан
көп
7
8
6
5
26
Барлығы
37
49
37
28
151
21. «STATISTICA» бағдарламасында Пирсон χ2 – белгісі сынағын орындаудың мысалы
1.2.
3.
4.
Деректерді енгізу.
«Basic statistics and
tables» модулі,
«Tables and banners»
рәсімі. Түйіндес
кестесі құру.
«Expected
frequencies»,
«Pearson & M-L Chisquare» опциялары.
Қорытынды кесте.
1
4
р>0,05 болғандық болжам
қабылданады, яғни мамандық
пен дәрігерге қаралу арасында
байланыс жоқ.
32
22.
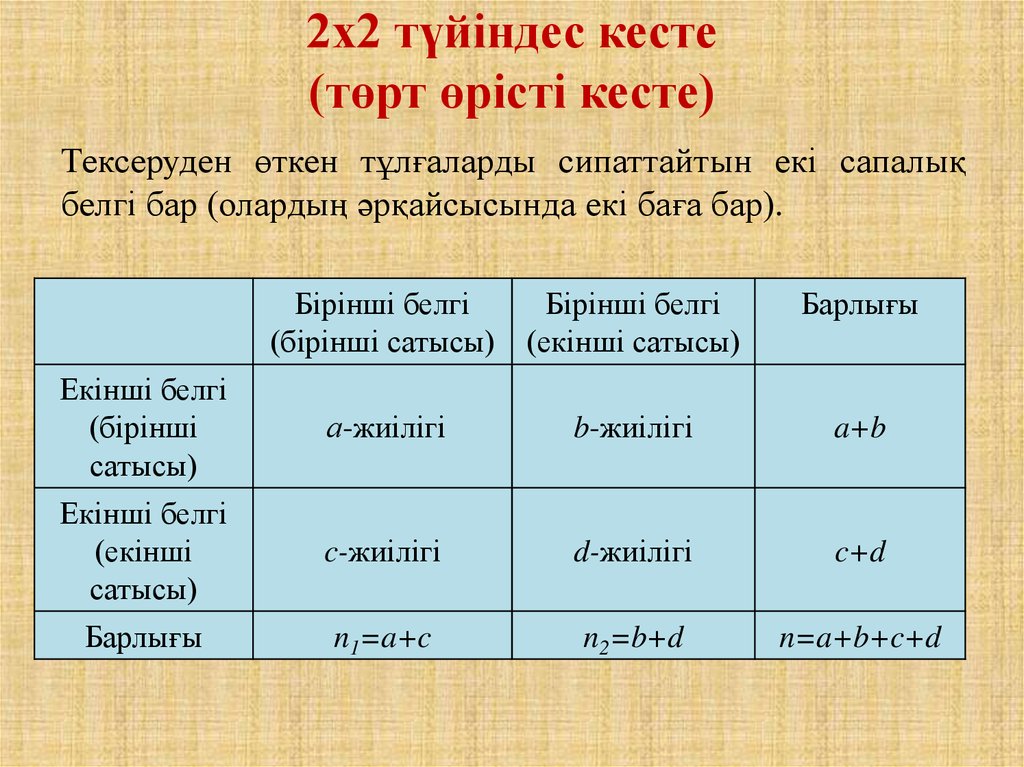
Биология және медицинада 2х2 өлшем түйіндескестелері өте жиі қолданылады.
23. 2х2 түйіндес кесте (төрт өрісті кесте)
Тексеруден өткен тұлғаларды сипаттайтын екі сапалықбелгі бар (олардың әрқайсысында екі баға бар).
Бірінші белгі
(бірінші сатысы)
Бірінші белгі
(екінші сатысы)
Барлығы
Екінші белгі
(бірінші
сатысы)
а-жиілігі
b-жиілігі
a+b
Екінші белгі
(екінші
сатысы)
c-жиілігі
d-жиілігі
c+d
Барлығы
n1=a+c
n2=b+d
n=a+b+c+d
24. Пирсонның χ2 –белгісін 2х2 кестесі үшін қолданудың тізбесі
1)Н0: бір белгінің кездесу жиілігі екінші белгінің кездесу
жиілігіне байланысты емес.
Н1: бір белгінің кездесу жиілігі екінші белгінің кездесу
жиілігіне байланысты.
2)
р=0,05 – маңыздылық деңгейі.
2
ad
bc
n
2
есеп
,
(a b)(c d )( a c)(b d )
3)
мұндағы a, b, c, d - түйіндес кестесіндегі жиіліктер.
2
4) кесте ( р, f ) , мұндағы f- еркіндік дәрежесі. Ол 2х2
түйіндес кестелер үшін f=1 (2 қосымшаны қара).
2
2
5) Егер есеп < кесте болса, онда «H0» қабылданады.
2
2
Егер есеп > кесте болса, онда «H0» қабылданбайды.
25.
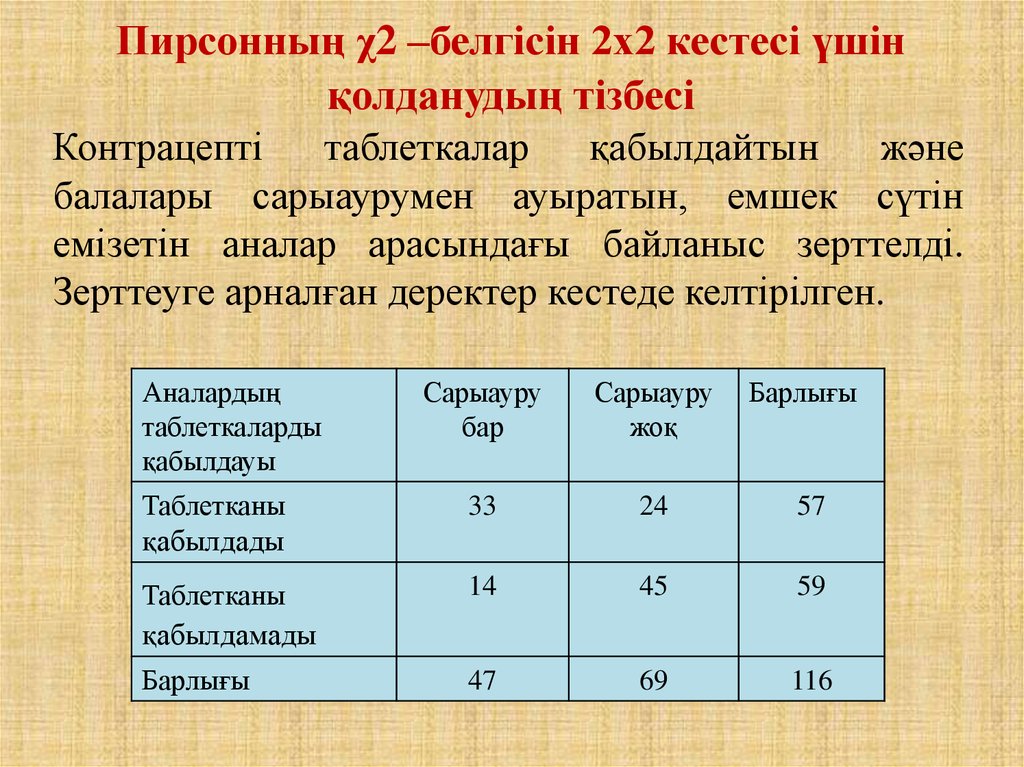
Пирсонның χ2 –белгісін 2х2 кестесі үшінқолданудың тізбесі
Контрацепті
таблеткалар
қабылдайтын
және
балалары сарыаурумен ауыратын, емшек сүтін
емізетін аналар арасындағы байланыс зерттелді.
Зерттеуге арналған деректер кестеде келтірілген.
Аналардың
таблеткаларды
қабылдауы
Сарыауру
бар
Сарыауру
жоқ
Барлығы
Таблетканы
қабылдады
33
24
57
Таблетканы
қабылдамады
14
45
59
Барлығы
47
69
116
26.
Пирсонның χ2 –белгісін 2х2 кестесі үшінқолданудың тізбесі
Шешуі.
Н0: балалардың сарыаурумен ауыруы анасының
контрацепті препаратты қабылдауына тәуелді емес.
Н1: балалардың сарыаурумен ауыруы анасының
контрацепті препаратты қабылдауына тәуелді.
2) р=0,05 – маңыздылық деңгейі
1)
3)
2
есеп
ad bc n
(33 45 24 14) 2 116
14,04
(a b)(c d )( a c)(b d )
57 59 47 69
2
кесте
(0,05;1) 3,8
2
4)
2
2
есеп
5)
> кесте болғандықтан, балалардың сарыаурумен
ауыруы анасының контрацепті препаратты қабылдауына
тәуелді болады.
27. χ2 Пирсон белгісінің кестелік мәніні
28. Дәріс жоспары
1. Түйіндес кестелер.2. Екі тәуелсіз популяцияның пропорциясын
салыстыру. Пирсонның χ2- келісім белгісі.
3. Йетс түзетуі.
4. Екі тәуелді популяцияның пропорциясын
салыстыру. Макнемардің χ2- белгісі
29. Йетс түзетуі.
2x2 кестесіндегі χ2 үшін келтірілген формула жоғарымәндер береді. Іс жүзінде, бұл нөлдік болжамның тым
жиі қабылданбауына алып келеді. Бұл әсерді
болдырмау үшін формулаға Йетс түзету енгізеді:
2
2
есеп
n
n ad bc
2
(a b)(c d )( a c)(b d )
Жоғарыда қарастырылған мысал
түзетуімен белгінің есептелген мәні:
2
2
есеп
үшін
Йетс
2
n
116
n ad bc
116 33 45 24 14
2
2
12,66
(a b)(c d )( a c)(b d )
57 59 47 69
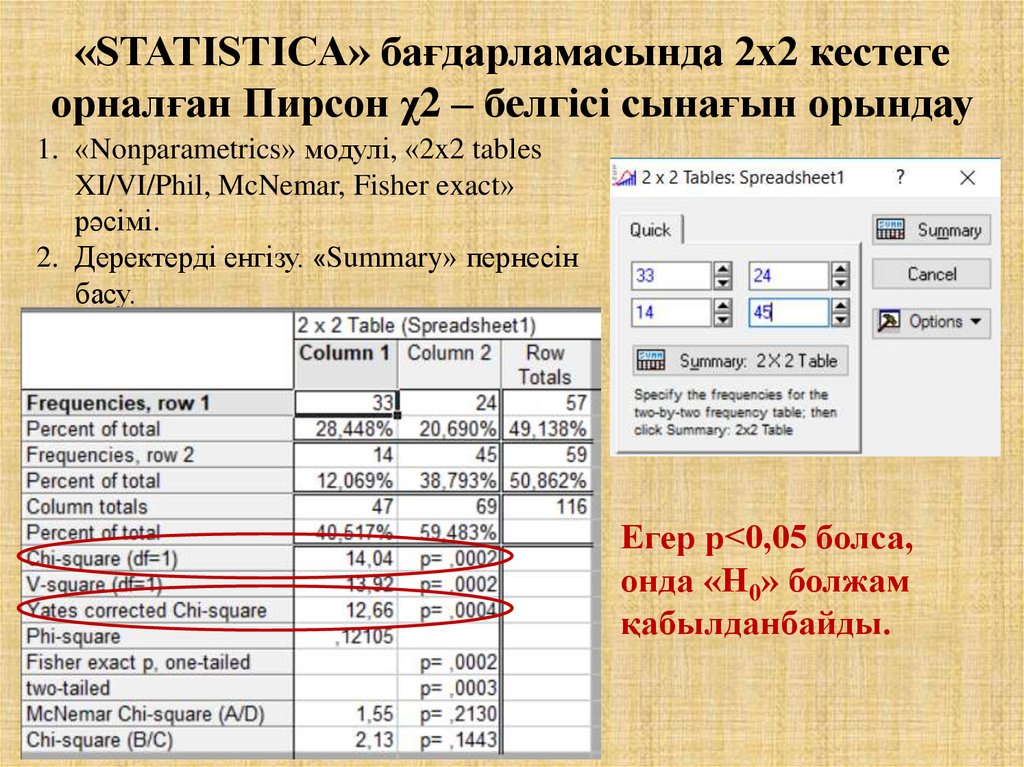
30. «STATISTICA» бағдарламасында 2x2 кестеге орналған Пирсон χ2 – белгісі сынағын орындау
1. «Nonparametrics» модулі, «2x2 tablesXI/VI/Phil, McNemar, Fisher exact»
рәсімі.
2. Деректерді енгізу. «Summary» пернесін
басу.
Егер p<0,05 болса,
онда «H0» болжам
қабылданбайды.
31. Дәріс жоспары
1. Түйіндес кестелер.2. Екі тәуелсіз популяцияның пропорциясын
салыстыру. Пирсонның χ2- келісім белгісі.
3. Йетс түзетуі.
4. Екі тәуелді популяцияның пропорциясын
салыстыру. Макнемардің χ2- белгісі
32.
Пирсонның χ2-белгісі тәуелсіз таңдамалардысалыстыру үшін қолданылады. Егер таңдамалар
тәуелді болса, онда Макнемардің χ2-белгісі
қолданылады.
Егер бірдей нысандарда екі байқау жасалса: «дейін»
және «кейін», онда таңдамалар тәуелді деп аталады.
Макнемардің χ2-белгісі тек 2x2 өлшемді түйіндес
кестелер үшін қолданылады.
33. Макнемардің χ2- белгісі
«кейінгі» белгі«дейінгі» белгі
«кейінгі» (-) екінші
сатысы
«кейінгі» (+) бірінші
сатысы
«дейінгі» (+)
бірінші сатысы
а (+) тен (-) ке өзгеру
саны
b (+) тің сақталу саны
«дейінгі» (-)
екінші сатысы
c (-) тің сақталу саны
d (-) тен (+) ке өзгеру
саны
34. Макнемардің χ2 – белгісін қолданудың тізбесі
1) Н0: фактор әсер еткеннен кейін белгі сатысының кездесужиілігі өзгерген жоқ.
Н1: фактор әсер еткеннен кейін белгі сатысының
кездесу жиілігі өзгерді.
2) р=0,05 – маңыздылық деңгейі
a d 1
2
3)
2
есеп
(a d )
2
кесте ( р, f ) ,
4)
мұндағы f - еркіндік дәрежесінің
саны. Ол 2х2 ұқсас кестелер үшін f=1 (2 қосымша).
2
2
есеп
5) Егер
< кесте болса, онда «H0» қабылданады.
2
Егер есеп > 2 кесте болса, онда «H0» қабылданбайды .
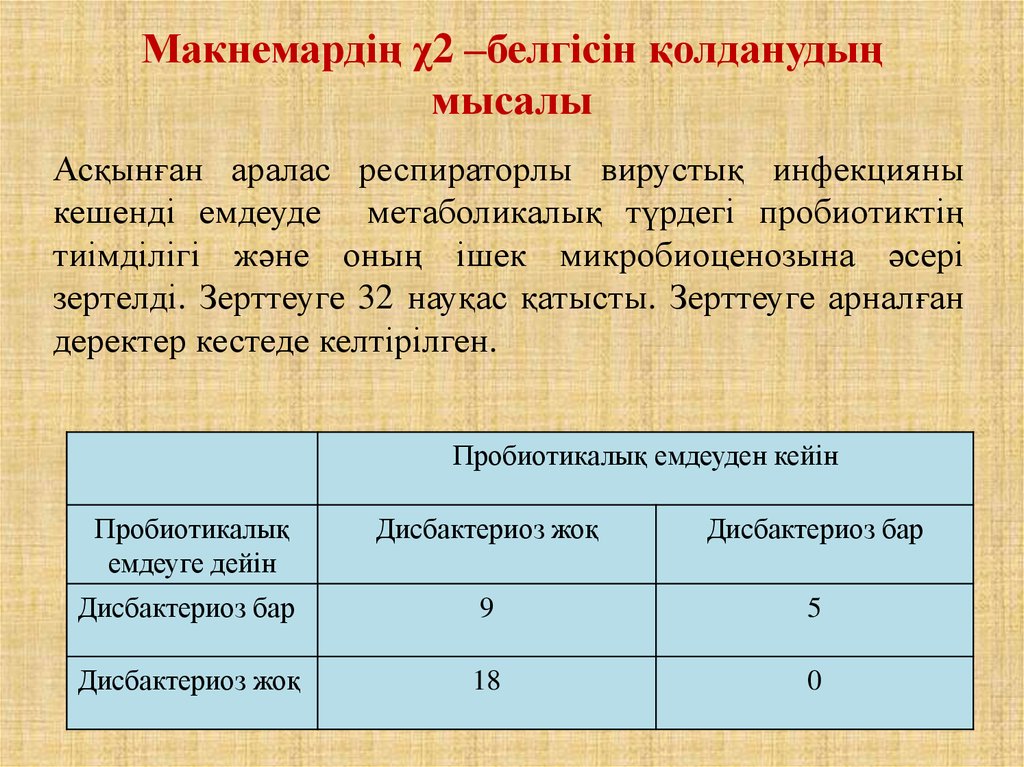
35. Макнемардің χ2 –белгісін қолданудың мысалы
Асқынған аралас респираторлы вирустық инфекцияныкешенді емдеуде метаболикалық түрдегі пробиотиктің
тиімділігі және оның ішек микробиоценозына әсері
зертелді. Зерттеуге 32 науқас қатысты. Зерттеуге арналған
деректер кестеде келтірілген.
Пробиотикалық емдеуден кейін
Пробиотикалық
емдеуге дейін
Дисбактериоз жоқ
Дисбактериоз бар
Дисбактериоз бар
9
5
Дисбактериоз жоқ
18
0
36.
Макнемардің χ2 –белгісін қолданудыңмысалы
Шешуі.
1) Н0: пробиотикті қолданғаннан кейін дисбактериоздың
жиілігі өзгерген жоқ.
Н1: пробиотикті қолданғаннан кейін дисбактериоздың
жиілігі өзгерді.
2) р=0,05 – маңыздылық деңгейі
2
2
a d 1
9 0 1
2
есеп
7,11
(a d )
(9 0)
3) кесте (0,05;1) 3,8 ,
2
2
есеп
5)
> кесте болғандық пробиотикті қолданғаннан кейін
дисбактериозбен ауыратын науқастардың саны өзгермегені
туралы болжам қабылданбайды.
2
37. χ2 Пирсон белгісінің кестелік мәніні
38. Бақылау сұрақтары:
1. Сапалыбелгілерді
талдаудың
ерекшелігі неде?
2. 2x2 түйіндес кесте дегеніміз не?
3. Пирсонның χ2 – белгісін қолдану
кезінде қандай шарттарды сақтау
керек?
4. Не үшін Йетс түзетулерін қолдану
керек?
5. Макнемардің χ2 – белгісі қандай
жағдайларда қолданылады?


























 Математика
Математика