Похожие презентации:
Комбинация геометрических тел
1.
Тема урока:Цели урока:
Образовательная: формировать знания, умения, навыки по построению
чертежей пространственных фигур;
Развивающая: совершенствовать навыки по решению стереометрических
задач на тему: “Комбинация геометрических тел”, развивать логическое
мышление, память, познавательный интерес, способствовать развитию
творческой деятельности, воображения;
Воспитательная: приучать к эстетическому оформлению записи в
тетради и выполнении чертежей, умению выслушивать других, прививать
трудолюбие, доброжелательность, воспитывать честность в оценке своих
знаний и знаний товарищей.
2.
32
4
1
к
у
2
п
т
о б р
л
а
п
е
3
ц
и
п р я
к р у г
о
5
ш
н
а з у ю щ а я
6
р
с
с
ф
4
д
е
и л и н д р
а
а
м о й
е
т
р
1
1
(по
4(по
вертикали):
2
(погоризонтали):
горизонтали):Тело,
3
(по
горизонтали):
4(по
горизонтали):
3
1
(по
(по
вертикали):
вертикали):Тело,
ТелоУгол
6
:
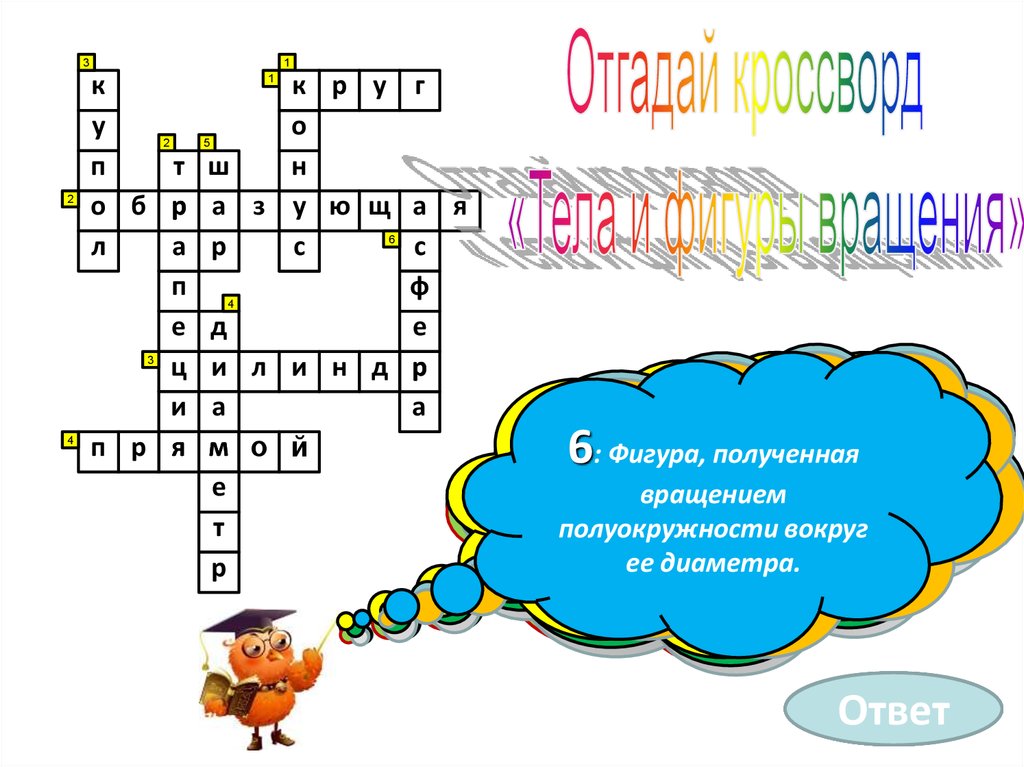
Фигура,
полученная
2
(по
вертикали):
Отрезок,
соединяющий
Фигура
на
плоскости,
все
Прямая,
при
вращении
5
: Тело,
полученное
между
высотой
и
полученное
вращением
вращения,
полученное
являющееся
вращением
вращением
Плоская
фигура,
при
две
точки
сферы
и
точки
которой
которой
вокруг
оси
плоскостью
основания
вращением
полукруга
прямоугольника
вокруг
верхней
прямоугольного
частью
полуокружности
проходящий
через
вокруг
вращении
которой
расположены
не
далее
конуса.
образуется
боковая
вокруг
его
диаметра.
одной
из
его
сторон.
центр
шара
треугольника
архитектурного
вокруг
ее
диаметра.
образуется
усеченный
данного
расстояния
от
поверхность цилиндра,
одного
сооружения.
изконус.
его
катетов.
одной
точки.
конуса.
Ответ
Ответ
3.
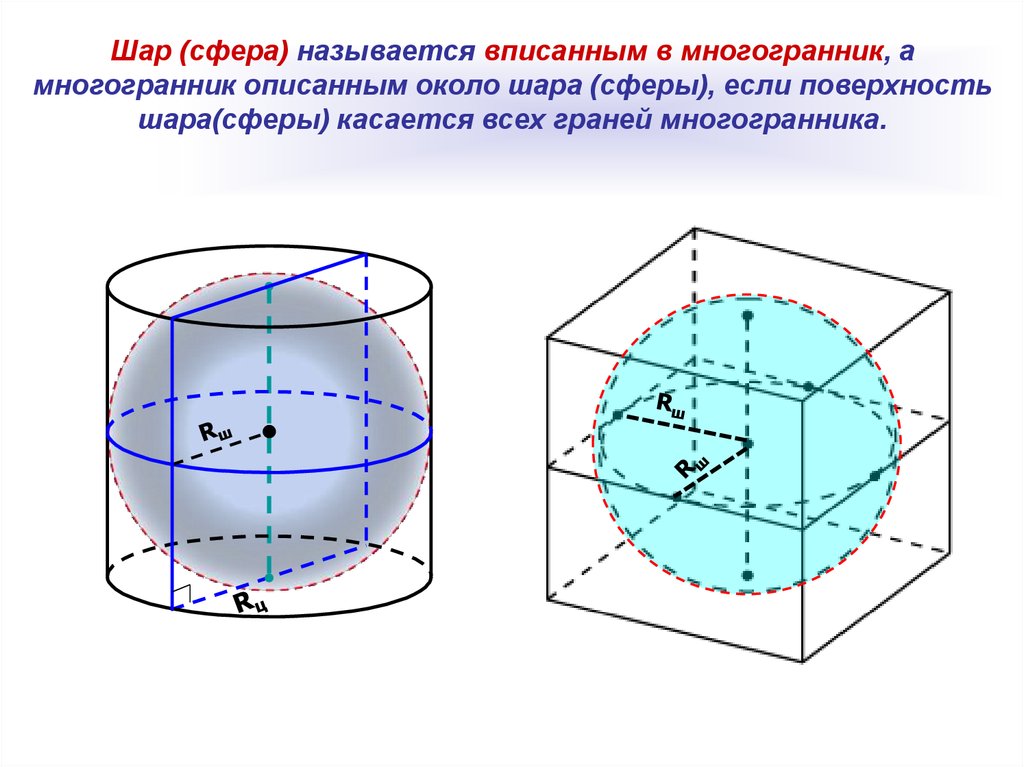
Шар (сфера) называется вписанным в многогранник, амногогранник описанным около шара (сферы), если поверхность
шара(сферы) касается всех граней многогранника.
4.
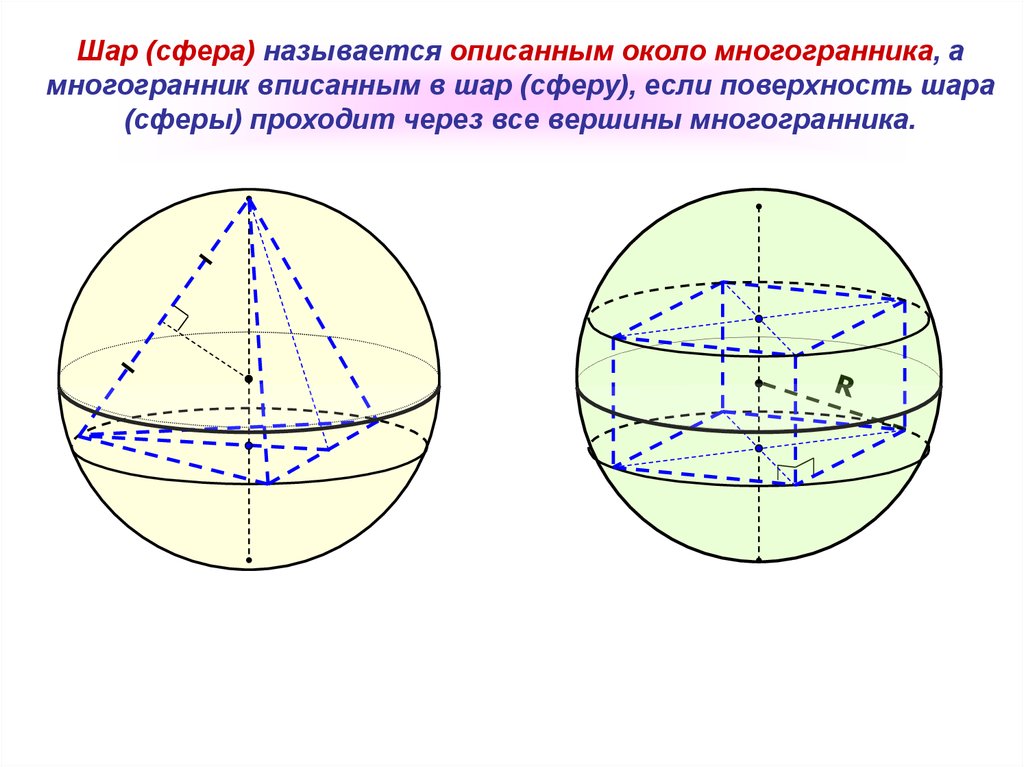
Шар (сфера) называется описанным около многогранника, амногогранник вписанным в шар (сферу), если поверхность шара
(сферы) проходит через все вершины многогранника.
5. Построение чертежей пространственных фигур
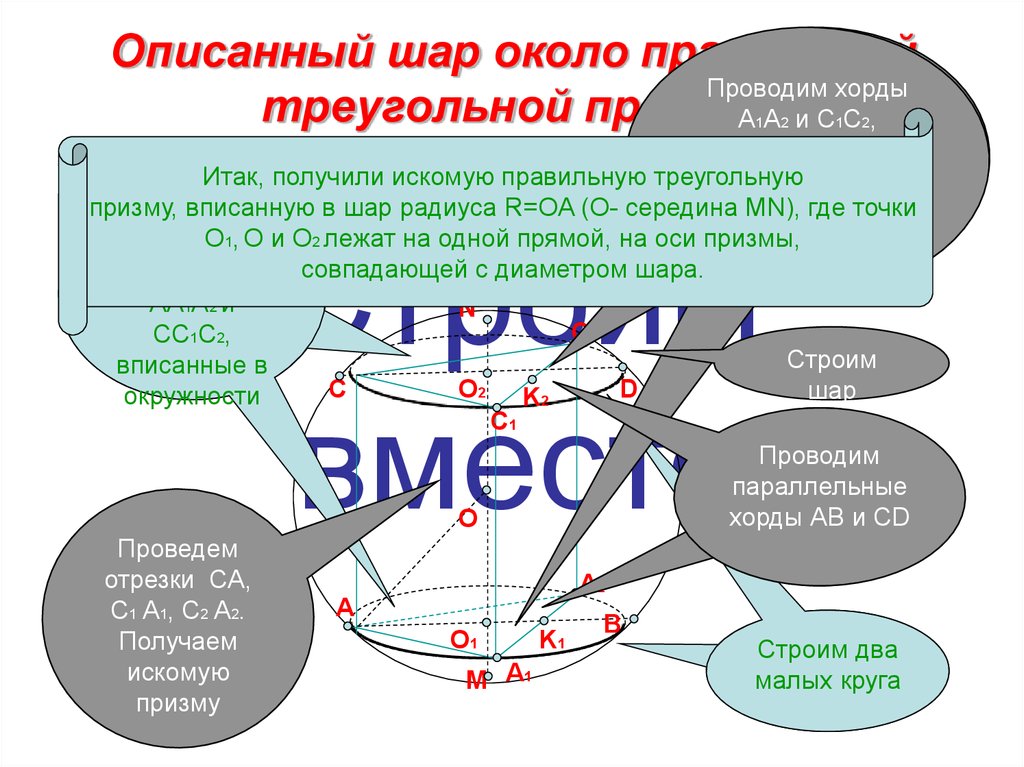
6. Описанный шар около правильной треугольной призмы
Описанный шар около правильнойПроводим хорды
треугольной призмы
AA иCC,
1
2
1
2
которые
Итак, получили искомую правильную треугольную
перпендикулярны
призму, вписанную в шар радиуса R=OA (О- середина
точки
AB MN),
и CDгде
и делят
O1, O и O2 лежат на одной прямой, на осиОпризмы,
Получаем
1В и О2D пополам
треугольники совпадающей с диаметром шара.
АA1A2 и
N
C2
СC1C2,
Строим
вписанные в
C
O2 K2
D
шар
окружности
C1
Проводим
параллельные
хорды АВ и СD
O
Проведем
отрезки CA,
A2
A
C1 A1, С2 A2.
B
O1
K1
Получаем
Строим два
искомую
M A1
малых круга
призму
Строим
вместе
7.
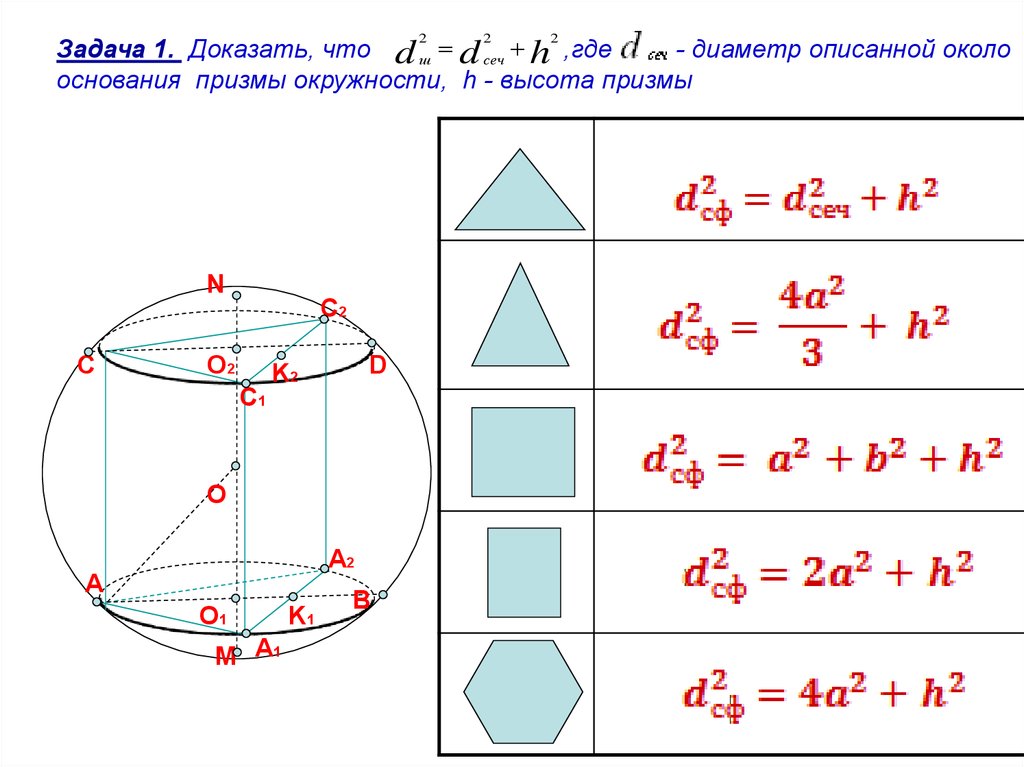
Задача 1. Доказать, что d ш d сеч h ,где- диаметр описанной около
основания призмы окружности, h - высота призмы
2
N
C2
C
O2
D
K2
C1
O
A2
A
O1
M A1
K1
B
2
2
8. Правильная пирамида, вписанная в сферу
Правильная пирамида,вписанная в сферуСтроим
Проводим хорду
ВС, которая
перпендикулярна
АD и делит О1D
пополам
Получаем
треугольник
ABC
шар
S
Строим
вместе
Проводим
хорду АD
O
Соединяем A
и S, B и S и D
и S.
Получаем
искомую
пирамиду
C
A
D
O1
B
M
Строим
малый круг
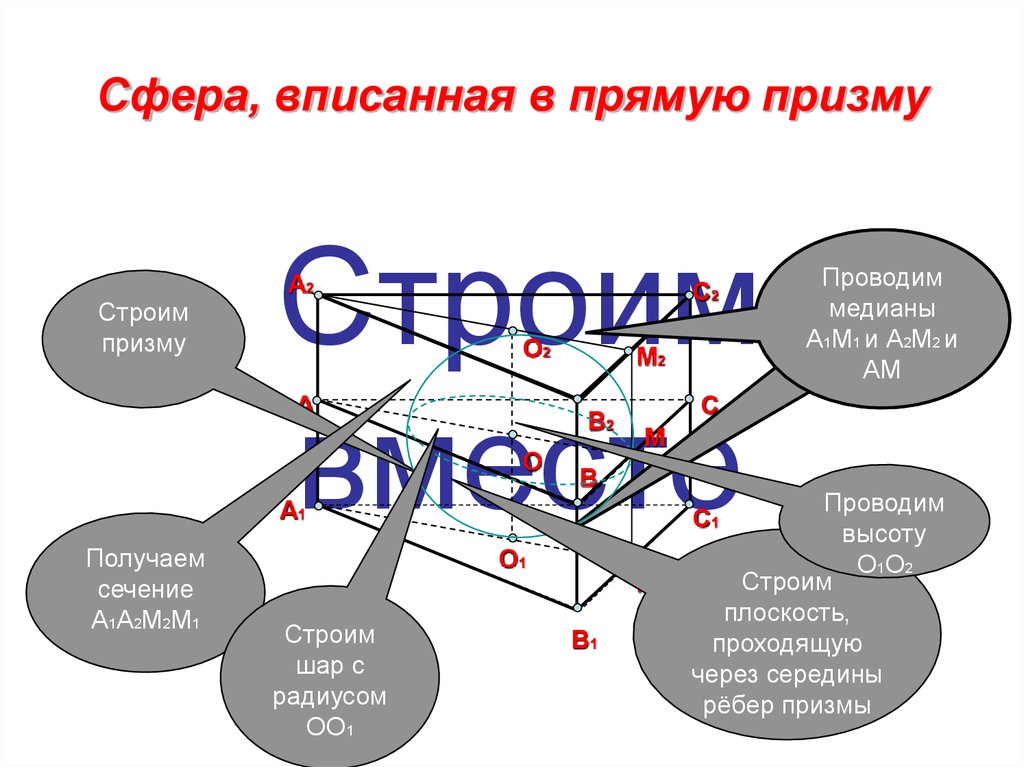
9. Сфера, вписанная в прямую призму
Строимпризму
Строим
вместе
A2
C2
O2
A
M2
B2
O
C
M
B
A1
Получаем
сечение
A1A2M2M1
Проводим
высоту
O 1O 2
Строим
плоскость,
проходящую
через середины
рёбер призмы
C1
O1
M1
Строим
шар с
радиусом
OO1
B1
Проводим
медианы
А1М1 и А2М2 и
АМ
10.
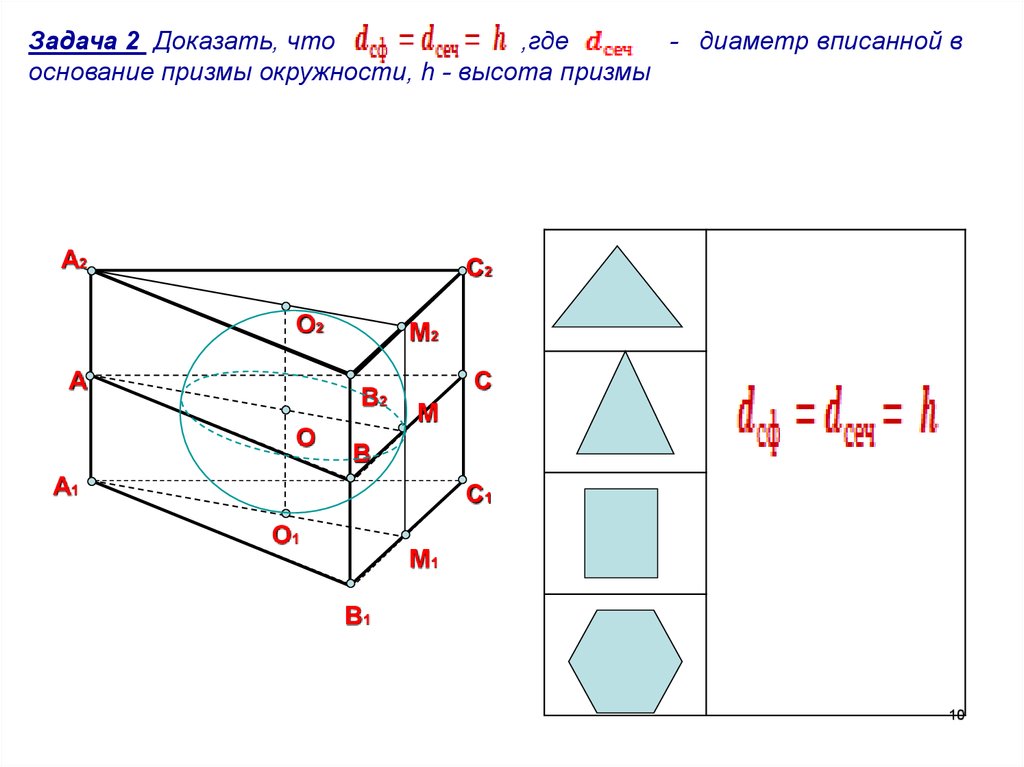
Задача 2 Доказать, что,где
- диаметр вписанной в
основание призмы окружности, h - высота призмы
A2
C2
O2
A
M2
B2
O
C
M
B
A1
C1
O1
M1
B1
10
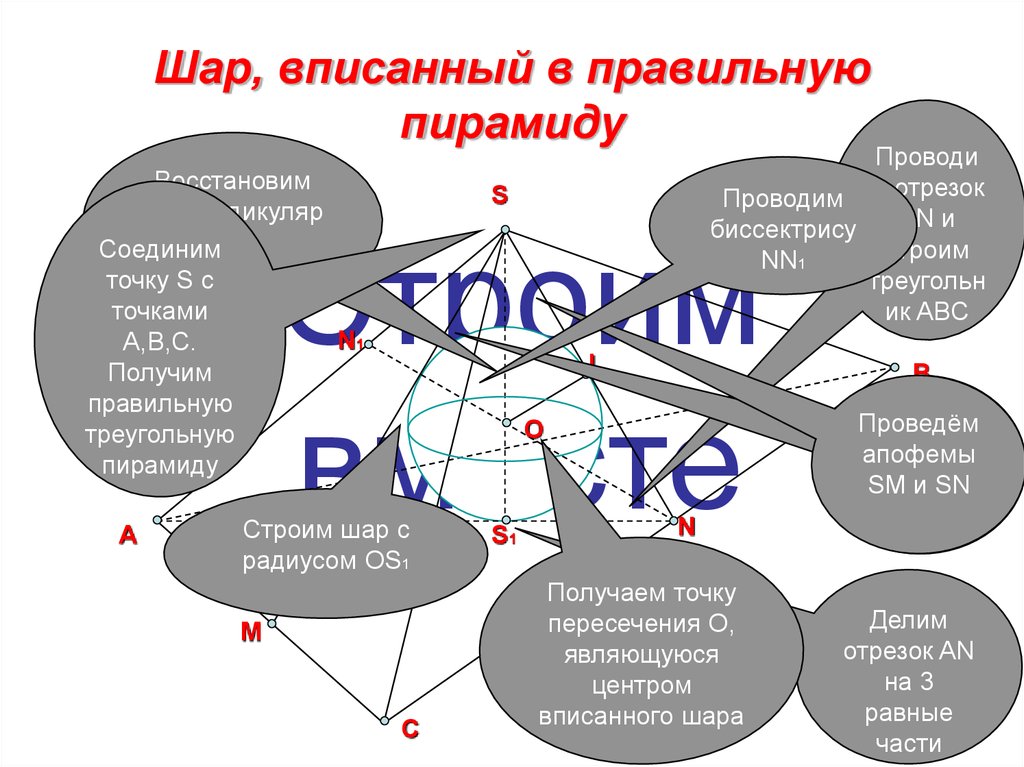
11. Шар, вписанный в правильную пирамиду
Восстановимперпендикуляр
СоединимSS1
точку S с
точками
N1
A,B,C.
Получим
правильную
треугольную
пирамиду
A
Проводи
Проводим м отрезок
AN и
биссектрису
строим
NN1
треугольн
ик ABC
S
Строим
вместе
L
O
Строим шар с
радиусом OS1
M
C
S1
B
Проведём
апофемы
SM и SN
N
Получаем точку
пересечения O,
являющуюся
центром
вписанного шара
Делим
отрезок AN
на 3
равные11
части
12. Задача 3. Вычислить поверхность шара, вписанного в треугольную пирамиду, все рёбра которой равны a.
План решения: 1) SK-?2) KO-? 3) SO-? 4) SM -? 5) MP-? 6) S пов
S
B
M
P
A
О
K
С
2
a
Ответ:
6
12
13. Итог урока
Выбор за вамиЯ ничего не понял и
с нетерпением ждал
конца урока
На уроке было
не интересно
Я все понял.
Урок понравился






 Математика
Математика








