Системы пропорционирования. Золотое сечение

1. Системы пропорционирования

Золотое сечение
Модулор Ле Корбюзье
Последовательность фибоначчи

2. Золотое сечение

• Законы, по которым создаются произведения искусства, принято
называть
законами
гармонии.
К
ним
относятся
равновесия, закон единства и соподчинения.
закон
Средствам
гармонизации относятся так же ритм, контраст, нюанс,
тождество, а также пропорции и масштаб.
• Обратим
внимание
на
одно
из
важнейших
средств
гармонизации — пропорции (связи частей и целого). Продолжая
тему единства целостного произведения, мы утверждаем, что
пропорции и есть именно то средство, в основе которого
заложена идея соотношения целого и составляющих это целое
частей. Под пропорцией понимается отношение частей целого
между собой и этим целым.

3. Золотое сечение

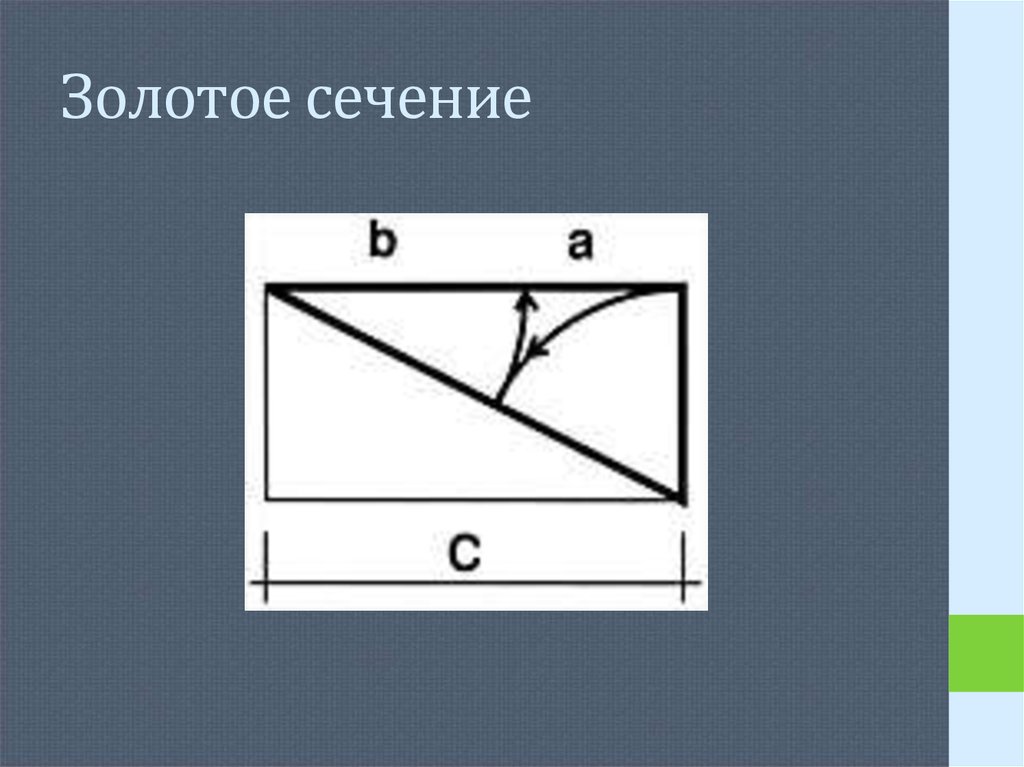
• Золотое сечение – это такое пропорциональное деление
отрезка на неравные части, при котором меньший отрезок
так относится к большему, как больший ко всему.
• a : b = b : c или с : b = b : а.

4. Золотое сечение

• К примеру, в правильной пятиконечной звезде, каждый
сегмент делится пересекающим его сегментом в золотом
сечении. Эти отношения равны 1.618. Число 1,618
называется коэффициентом золотого сечения.
• Построим отрезки в пропорциях золотого сечения. В
прямоугольнике с соотношением сторон 1:2 проводится
диагональ, на которую поворотом накладывается меньшая
сторона. Остаток диагонали поворачивается вокруг
вершины прямоугольника до совмещения с положением
верхнего основания. Таким образом, верхнее основание
поделилось на два неравных отрезка в пропорции
золотого сечения.

5. Золотое сечение

6. Золотое сечение

• Принято считать, что понятие о золотом сечении ввел в
научный обиход Пифагор.
• Есть
предположение,
что
Пифагор
свое
знание
позаимствовал у египтян и вавилонян. И действительно,
пропорции
пирамиды
Хеопса,
храмов,
барельефов,
предметов быта и украшений из гробницы Тутанхамона
свидетельствуют, что египетские мастера пользовались
соотношениями золотого деления при их создании.

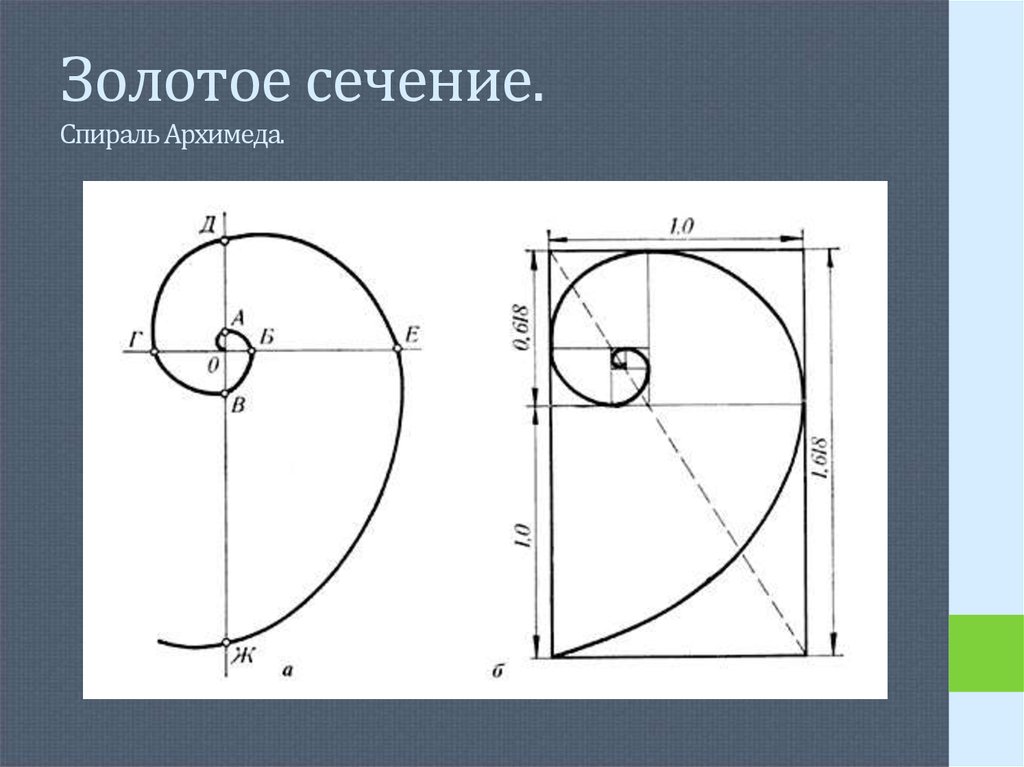
7. Золотое сечение. Спираль Архимеда.

8. Золотое сечение. Спираль Архимеда.

9. Золотое сечение

10. Золотое сечение

11. Золотое сечение.

12. Золотое сечение.

13. Золотое сечение

14. Последовательность Фибоначчи.

С историей золотого сечения косвенным образом связано имя
итальянского математика монаха Леонардо из Пизы, более известного
под именем Фибоначчи (сын Боначчи). В 1202 г вышел в свет
математический труд Фибоначчи «Книга об абаке» (счетной доске), в
котором были собраны все известные на то время задачи. Одна из задач
гласила «Сколько пар кроликов в один год от одной пары родится».
Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы
0 1 2 3 4 5 6 7 8
9 10
Пары кроликов
0 1 1 2 3 5 8 13 21 34 55
11
12 и т.д.
89 144 и т.д.

15. Как рассчитать золотое сечение?

Числа ряда Фибоначчи часто используются в дизайне для вычисления
пропорций, т.к. работать с ними легче, чем с числом 1,618.
Пара удобных приложений, которые помогут вычислить Золотое сечение.
Phiculator - http://www.thismanslife.co.uk/main.asp?contentid=phiculator –
маленькая и удобная программка, которая из любого введенного числа,
автоматически вычислит, соответствующее Золотому сечению, значение.
Golden Section Ratio Design Tool - http://www.atrise.com/golden-section – а
это уже солидный инструмент, который поможет избежать рутинных
операций при работе с компоновкой объектов и форм. Результат можно
увидеть на лету.

16. Где применяется золотое сечение?

Самым главным остается вопрос, зачем дизайнеру эта математика и
какой в ней практический смысл? А смысл есть. Например, отношение
сторон у iPod Shuffle 1.59, iPod Classic 1.67, а у iPhone4 1.7 – объем продаж
за первые 4 дня торговли превысил 1 миллион 700 тысяч штук.

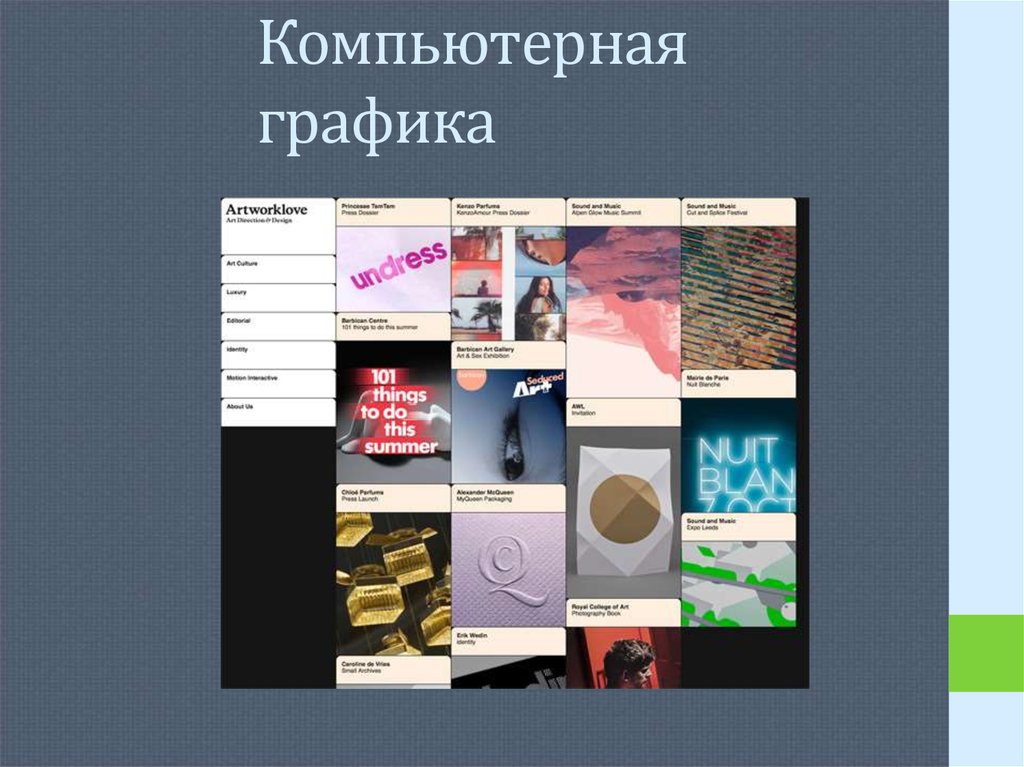
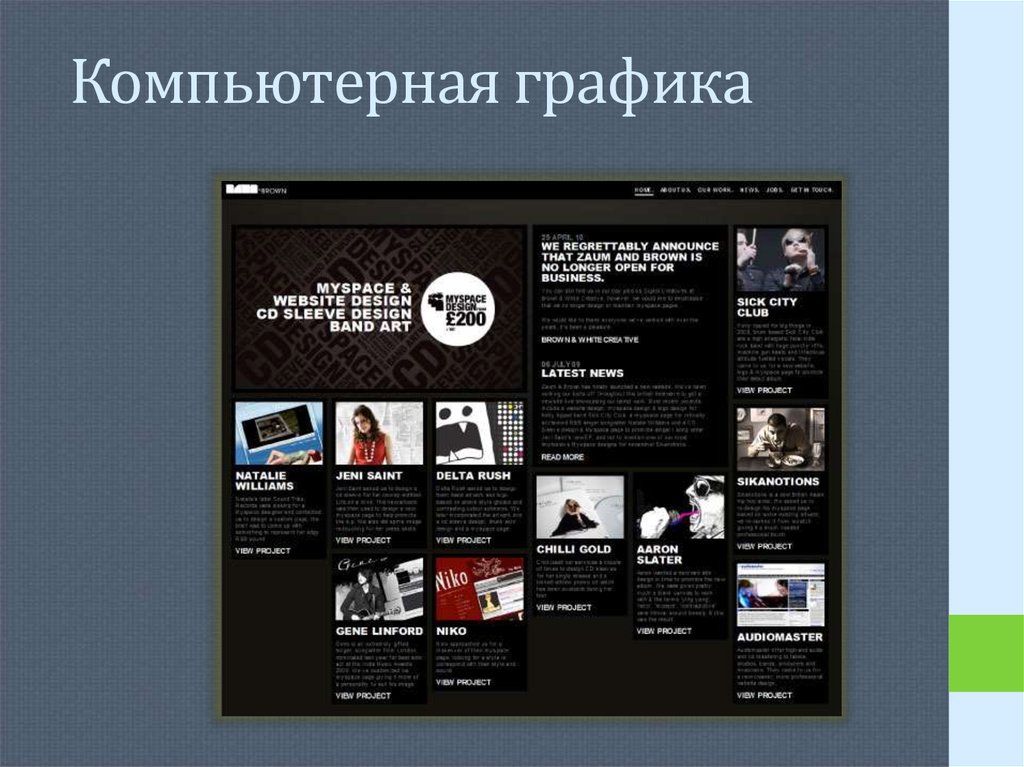
17. Компьютерная графика

Примером использования правила «Золотого сечения» может являться
расположение основных компонентов изображения в особых точках —
«зрительных центрах». Часто используются четыре точки, расположенные на
расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.

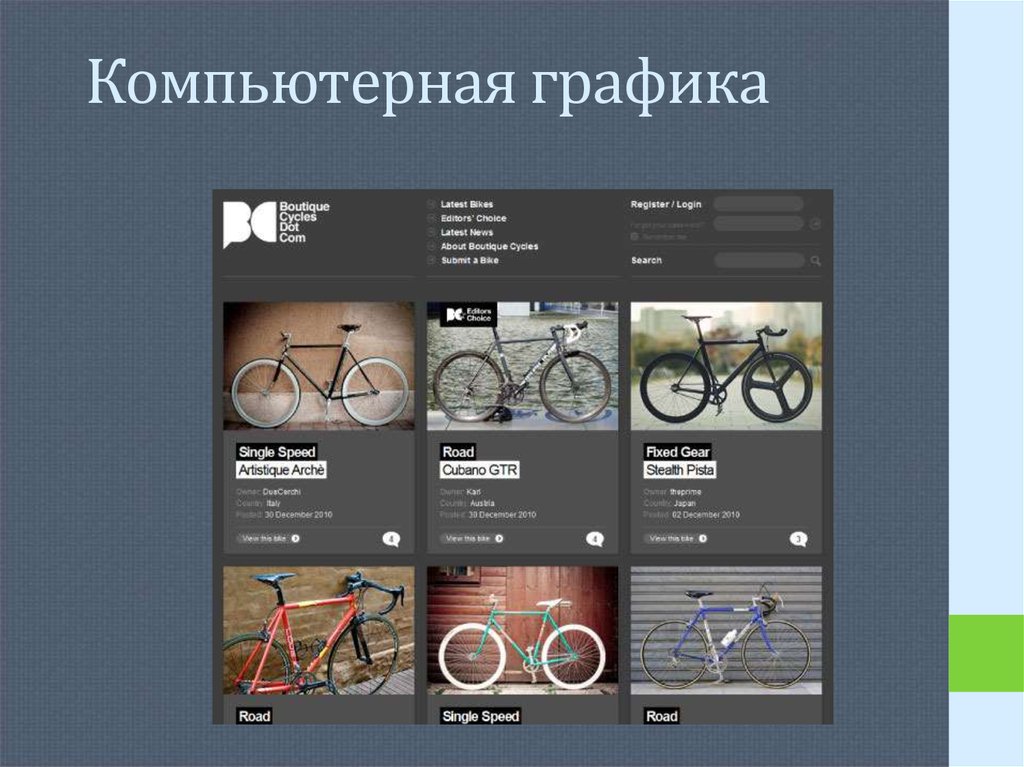
18. Компьютерная графика

Применение «зрительных точек» находящихся на третях соотношения высоты и
ширины.

19. Как применяется золотое сечение?

Принцип золотого сечения на практике в Web поможет определить,
какого размера должны быть элементы на странице, в каком месте и на
каком расстоянии они должны располагаться друг от друга, чтобы не
нарушать баланс, чтобы сайт выглядел гармоничным.
Правило третей позволяет определить точки визуального восприятия на
странице, для этого поделим страницу на три части по горизонтали и
вертикали.
На пересечении линий находятся 4 важные точки, которые можно
использовать для выделения основных деталей макета сайта.
Как правило, не стоит использовать сразу все четыре точки, но, одну или
две – обязательно.

20. Как применяется золотое сечение?

Важную деталь лучше поместить в левый верхний угол, т. к. пользователи
начинают просматривать сайт именно оттуда – логотип, контактную
информацию и пр.
Навигационное меню можем расположить на первой горизонтальной
линии.
Еще один-два важных элемента располагают на точках пересечения
горизонтальных и вертикальных линий.
Таким образом наиболее важные вещи помещены в местах наибольшего
внимания пользователя. При таком расположение элементов сайт
становится более удобным и более структурированным для просмотра.

21. Модульная сетка

Сетка – один из самых известных приёмов дизайнеров, который
позволяет создавать ровные и пропорциональные макеты. Существует
множество видов сеток, и ресурсов, посвященных им.
Чаще всего модульная сетка строится по принципу квадрата или
прямоугольника и его кратных повторений.
Чаще всего используют отношения, целых модулей или 0,5 и 1,5 модуля.

22. Компьютерная графика

23. Компьютерная графика

24. Компьютерная графика

25. Компьютерная графика

26. Спасибо за внимание