Похожие презентации:
Соотношения между сторонами и углами треугольника
1. Соотношения между сторонами и углами треугольника
Проект по геометриивыполнила Манасян Луиза
ученица 7 в класса. Учитель
Садыкова Лилия Ренатовна
2. Теорема о сумме углов треугольника
ТеоремаСумма углов
треугольника равна
180⁰
Теорема
Внешний угол
треугольника равен
сумме двух углов
треугольника
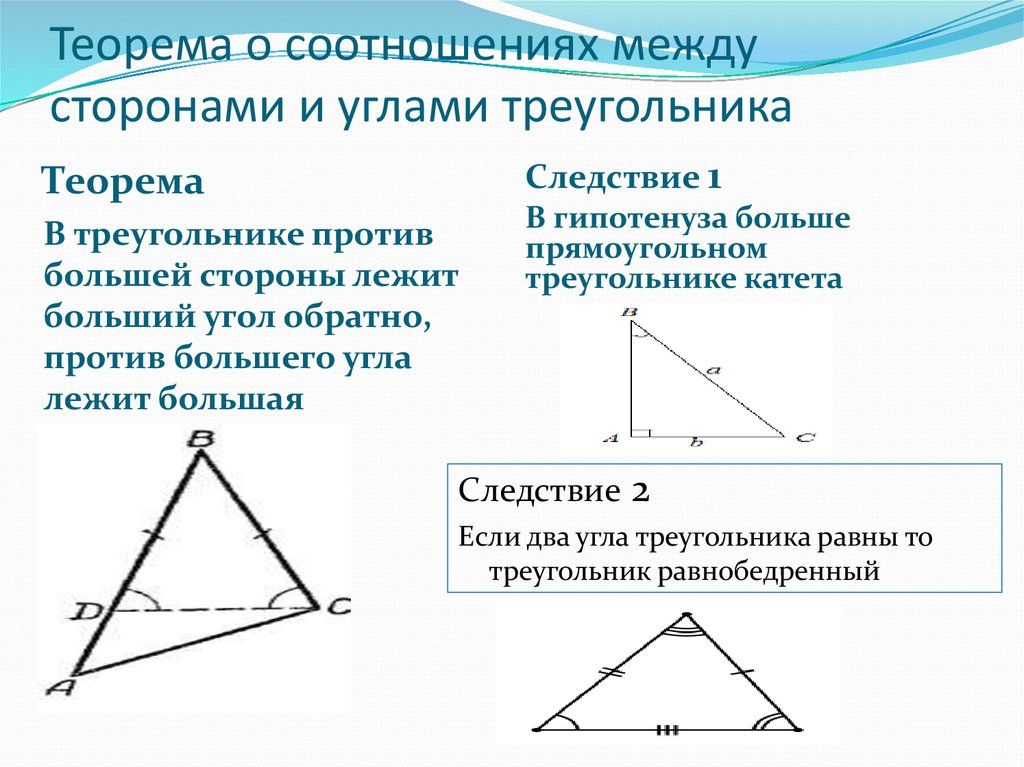
3. Теорема о соотношениях между сторонами и углами треугольника
ТеоремаСледствие 1
В треугольнике против
большей стороны лежит
больший угол обратно,
против большего угла
лежит большая
В гипотенуза больше
прямоугольном
треугольнике катета
Следствие 2
Если два угла треугольника равны то
треугольник равнобедренный
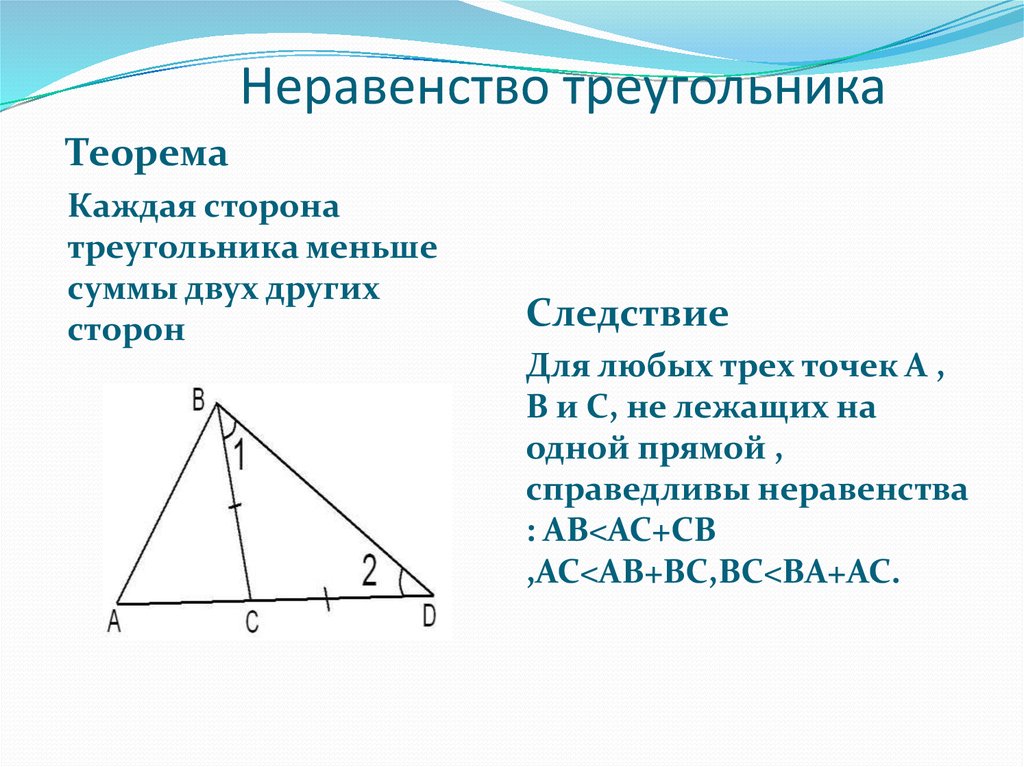
4. Неравенство треугольника
ТеоремаКаждая сторона
треугольника меньше
суммы двух других
сторон
Следствие
Для любых трех точек А ,
В и С, не лежащих на
одной прямой ,
справедливы неравенства
: AB<AC+CB
,AC<AB+BC,BC<BA+AC.
5. Если катет прямоугольного треугольника равен половине гипотенузы то угол лежащий против этого катета равен 30 градусов
Катет прямоугольноготреугольника лежащий
против угла в 30 градусов
равен половине
гипотенузы
Сумма двух острых углов
прямоугольного
треугольника равна 90⁰
6. Признаки равенства прямоугольных треугольников .
Из второго признака равенстваИз первого признака
равенства треугольников
следует :
Если катеты одного
прямоугольного треугольника
соответственно равны катетам
другого , то такие
треугольники равны .
треугольников следует :
Если катет и прилежащий к нему
острый угол одного
прямоугольного треугольника
соответственно равны катету и
прилежащему к нему острому углу
другого , то такие треугольники
равны.
7. Признаки равенства прямоугольных треугольников
Теорема :Теорема:
Если гипотенуза и катет
Если гипотенуза и катет
одного прямоугольного
одного прямоугольного
треугольника
треугольника
соответственно равны
соответственно равны
гипотенузе катету
гипотенузе и острому углу
другого , то такие
другого ,то такие
треугольники равны.
треугольники равны .
8. Расстояние от данной точки до прямой. Расстояние между параллельными прямыми.
Обратное доказанной теореме:Теорема
Все точки каждой из двух
параллельных прямых
равноудалены от другой
прямой.
Все точки плоскости
расположенные по одну сторону от
данной прямой и равноудалённые
от неё лежат на прямой
параллельной данной .
Из доказанной теоремы и ей
обратной следует ,что множества
всех точек плоскости находящихся на
заданном расстоянии от данной
прямой и лежащих по одну сторону то
неё , есть прямая ,параллельная
данной прямой .








 Математика
Математика








