Похожие презентации:
Производная интеграла по переменному верхнему пределу
1.
Лекция 91. Производная интеграла по переменному
верхнему пределу .
При изменении верхнего предела величина
интеграла будет изменяться, то есть интеграл
можно рассматривать как функцию верхнего
x
предела:
F ( x)
f (t ) dt
d
F ( x ) называется интегралом с переменным
верхним пределом.
2.
ТЕсли
то
f (t )
непрерывна на [a,b],
F '( x )
f t dt f ( x )
d
x
Доказательство
По определению производной
F ( x x ) F ( x )
F '( x ) lim
x 0
x
3.
Рассмотрим приращение F(x) :x x
x
d
d
f ( t )dt
F ( x x ) F ( x ) f ( t )dt
x
x x
x
d
x
d
f ( t )dt
f
(
t
)
dt
f
(
t
)
dt
x x
f
(
c
)
x
;
f
(
t
)
dt
x c x x
x
( По теореме о среднем )
4.
F ( x x ) F ( x )lim
x 0
x
lim f (c ) f ( x );
x 0( c x )
F '( x ) f ( x )
5.
Следствие:Всякая непрерывная на [a,b]
f ( x)
имеет на этом отрезке первообразную :
x
F ( x)
f
(
t
)
dt
,или
a
x
F ( x)
f ( t )dtС
a
(т.к. первообразная определена с точностью до
произвольной постоянной)
6.
2. Формула Ньютона-Лейбница.Т
Если
f ( x)
непрерывна на [a,b], то
b
f ( x)dx F (b) F (a)
a
F (b) F (a) F ( x) обозначение
b
a
7.
Доказательство:Раз функция f(x) непрерывна, то она имеет
x
первообразную
F ( x)
f
(
t
)
dt
C
a
Положим
x a
a
F (a )
f ( t )dt C C
Положим
a
x b
b
F (b )
f ( t )dt F (a )
a
8.
bb
a
a
f
(
t
)
dt
f
(
x
)
dx
F (b) F (a );
Следовательно, для вычисления определенного
интеграла нужно:
1) Найти
F ( x );
2) вычислить
F (b) F (a ).
9.
Примеры.b
b
2 b
x
1)
kx dx k x dx k
a
2
a
a
k 2 2
b a ;
2
10.
2)sin x dx cos x cos cos0
0
0
1 1 2
11.
Замена переменной в определенноминтеграле .
3.
Т
Если
1) f ( x )
непрерывна на
2) x g( t )
a, b ,
непрерывно дифференцируема
на ,
3) a g( ); b g ( ),
12.
тоb
f ( x )dx
f ( g ( t )) g '( t ) dt
a
Доказательство.
Пусть F(x) – первообразная для f(x),тогда
b
f ( x )dx F (b ) F (a )
a
13.
f(
g
(
t
))
g
'(
t
)
dt
f
(
g
(
t
))
dg
(
t
)
F ( g( )) F ( g( )) F (b) F (a )
14.
Примеры.r
1)
r
x
dx
2
2
0
0 r sin
, :
r r sin
/2
x r sin t
dx r cos tdt
0
/2
r
r
sin
t
r
cos
tdt
2
0
2
2
15.
2 /2/2
r
r cos t
r cos tdt
2
0
2
r
2
/2
1
t sin 2t
2
0
1 cos 2t dt
0
r
.
4
2
16.
22)
x
1
dx
1 x
2
1
1
, :
1
2
1
x
t
dt
dx 2
t
1
1/ 2
1/ 2
t
2
dt
2
2
1 t
t
1
17.
11
1 t
1/ 2
2
dt ln t 1 t
2
1 5
ln 1 2 ln
2
ln
2(1 2)
1 5
;
1
1/ 2
18.
Интегралы от чётных и нечётных функцийв симметричных пределах.
I . f ( x)
чётная функция.
f ( x ) f ( x )
a
0
a
a
a
0
f
(
x
)
dx
f
(
x
)
dx
f
(
x
)
dx
;
0
f
(
x
)
dx
a
x t
dx dt
a; 0
19.
0f ( t ) dt
a
a
f
(
t
)
dt
0
a
a
a
0
a
f
(
x
)
dx
;
0
f
(
x
)
dx
2
f
(
x
)
dx
20.
II . f ( x )нечётная функция.
f ( x ) f ( x )
a
0
a
a
a
0
f
(
x
)
dx
f
(
x
)
dx
f
(
x
)
dx
;
0
f ( x )dx
a
x t
dx dt
a; 0
21.
0f ( t ) dt
a
a
f ( t ) dt
0
a
a
0
0
f ( t ) dt
f ( x ) dx;
a
f
(
x
)
dx
0
a
22.
Интегрирование по частям в определенноминтеграле.
4.
Т
Если u( x ), v ( x ) имеют на [a,b]
непрерывные производные, то
b
b
b
udv u v vdu
a
a
a
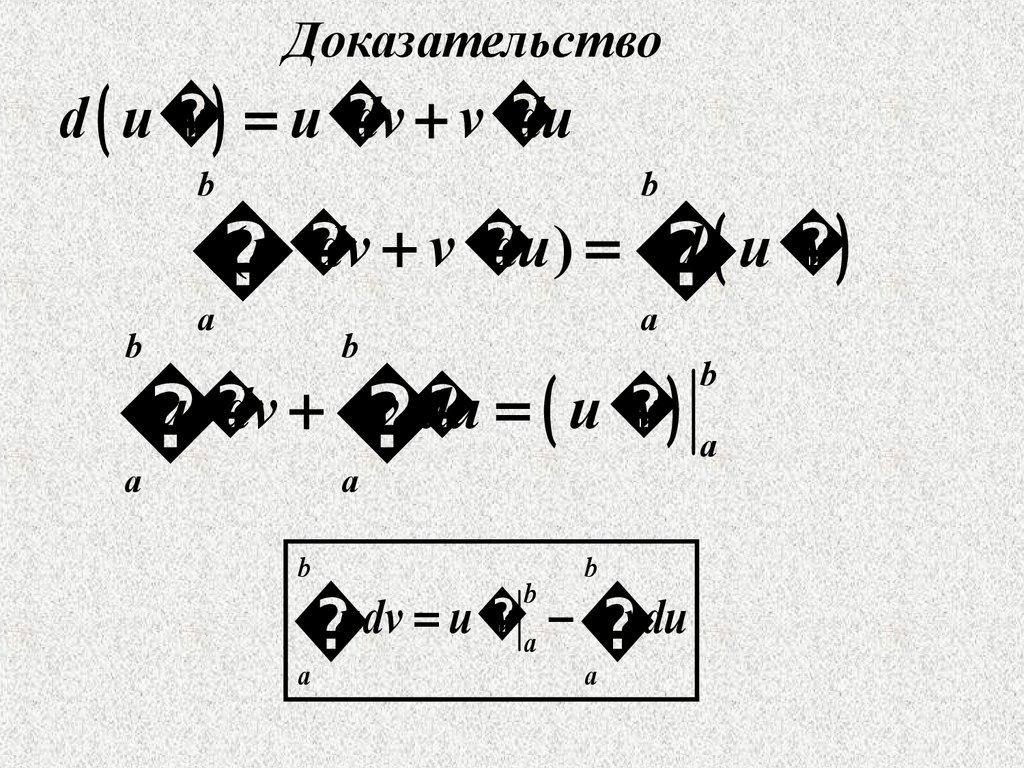
23.
Доказательствоd u
v u
dv v
du
b
b
a
a
(
u
dv
v
du
)
d
u
v
b
b
u
dv
v
du u
v
a
a
b
b
b
udv u v vdu
a
a
a
b
a
24.
Пример.1
u arctgx; dv dx;
arctgx
dx
dx
du
;
v
x
2
1 x
0
1
xdx
x
arctgx 0 2
1 x
0
1
25.
12
ln 1 x
4 2
1
0
1
ln 2.
4 2








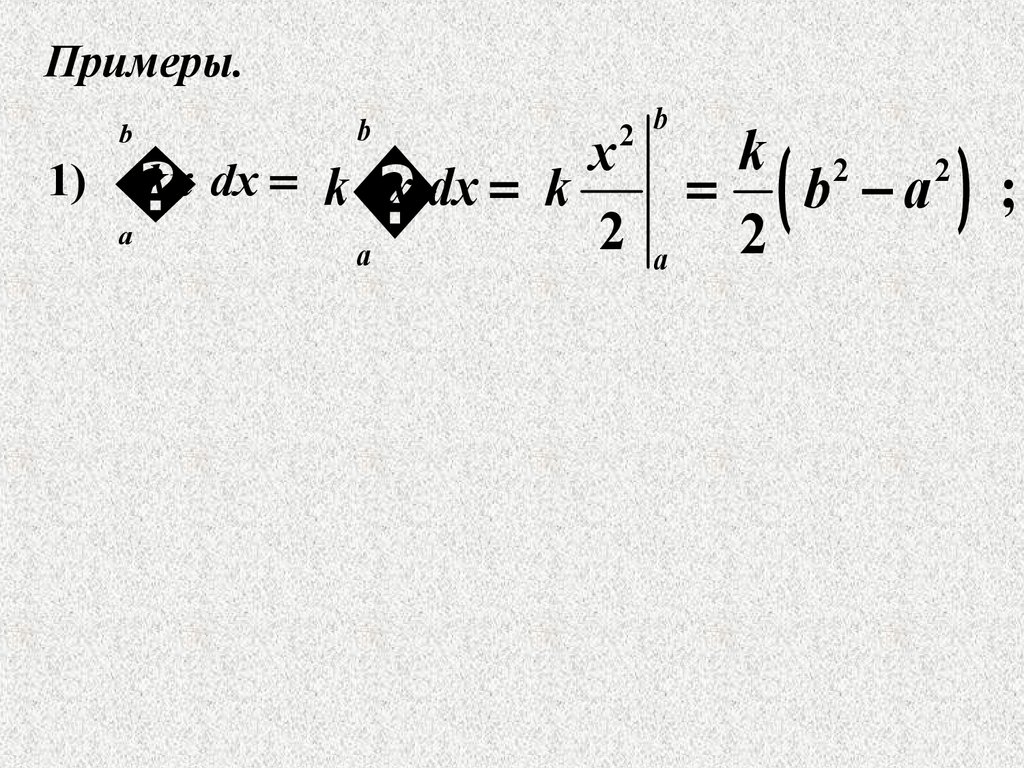
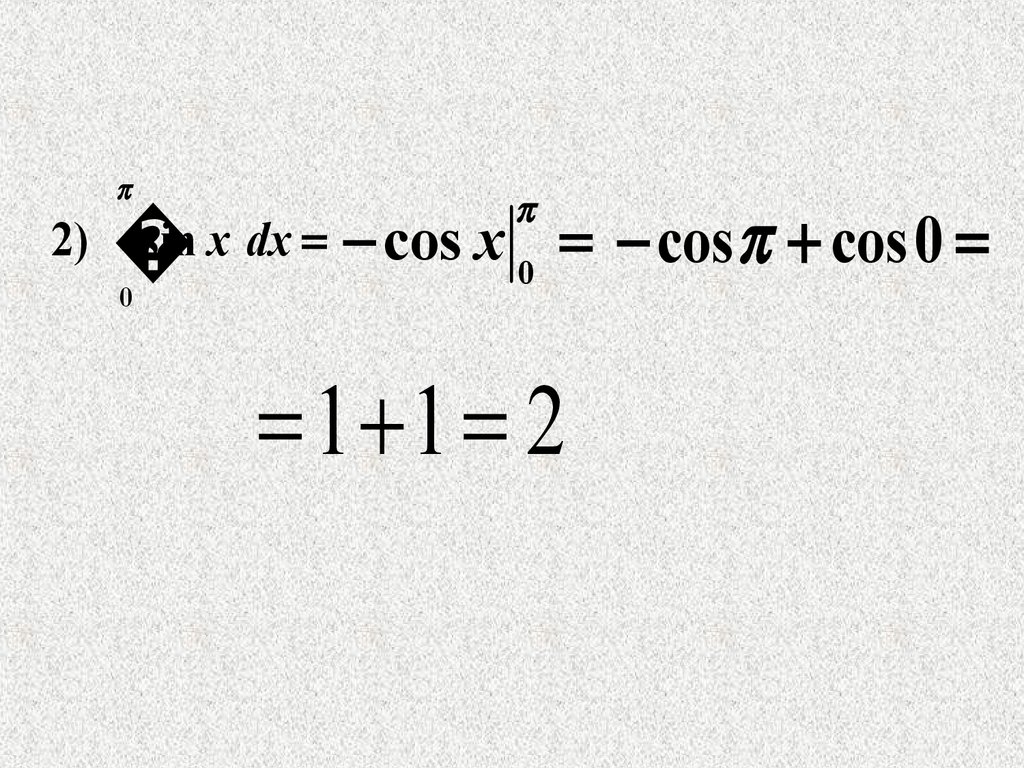

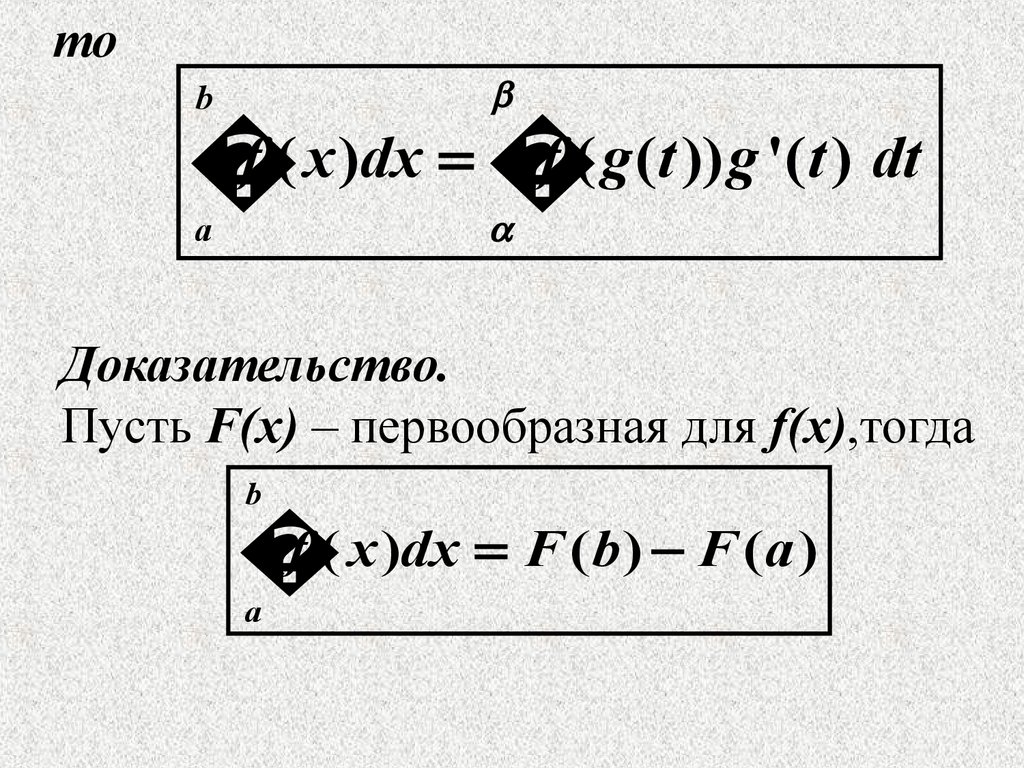
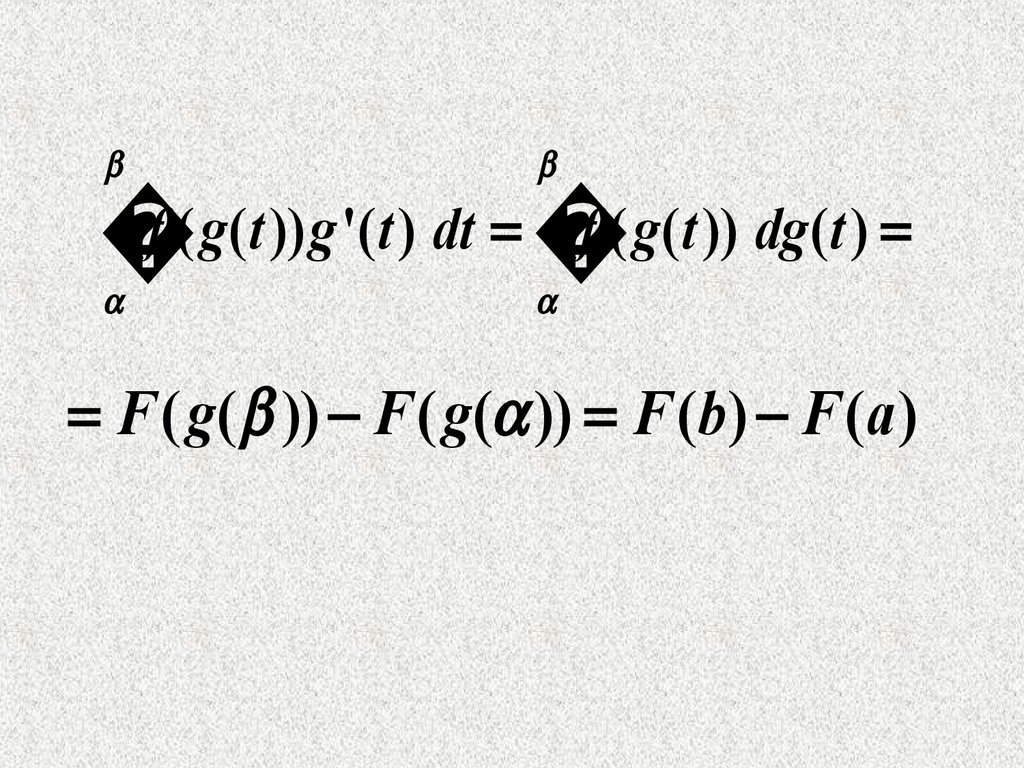







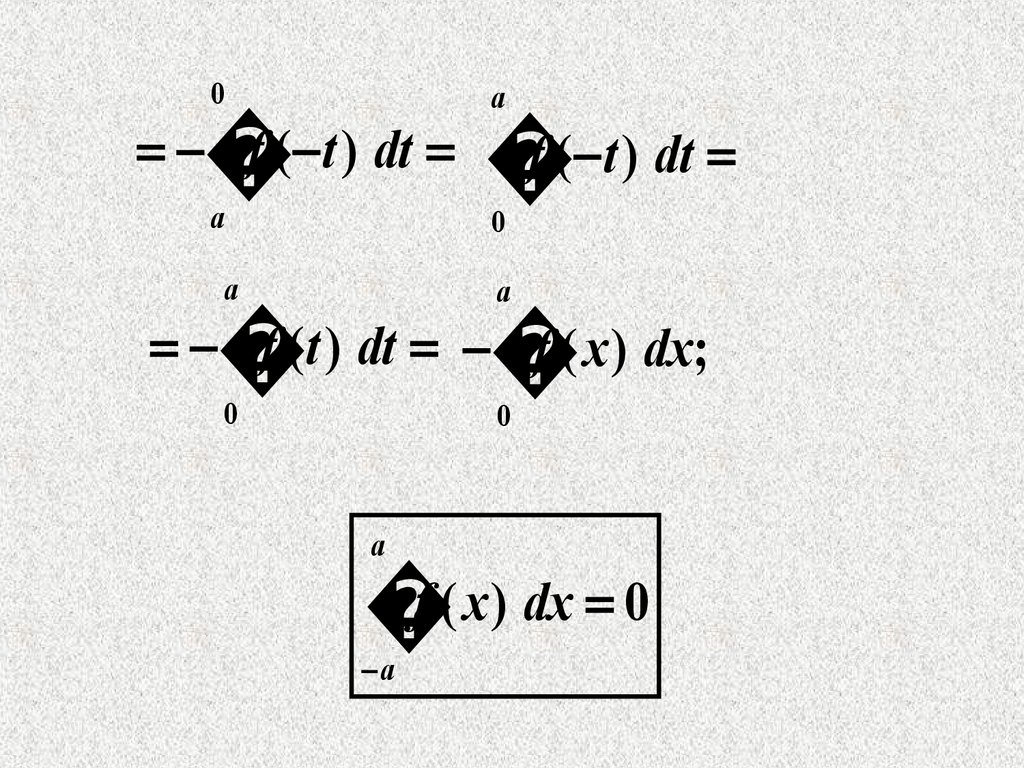

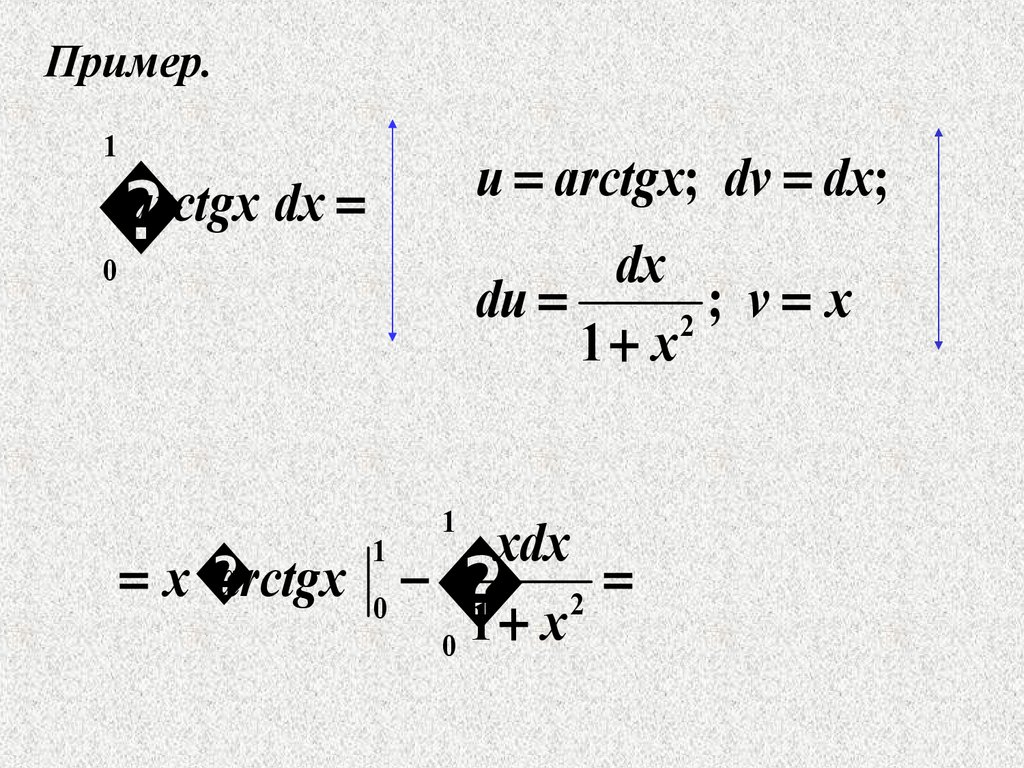
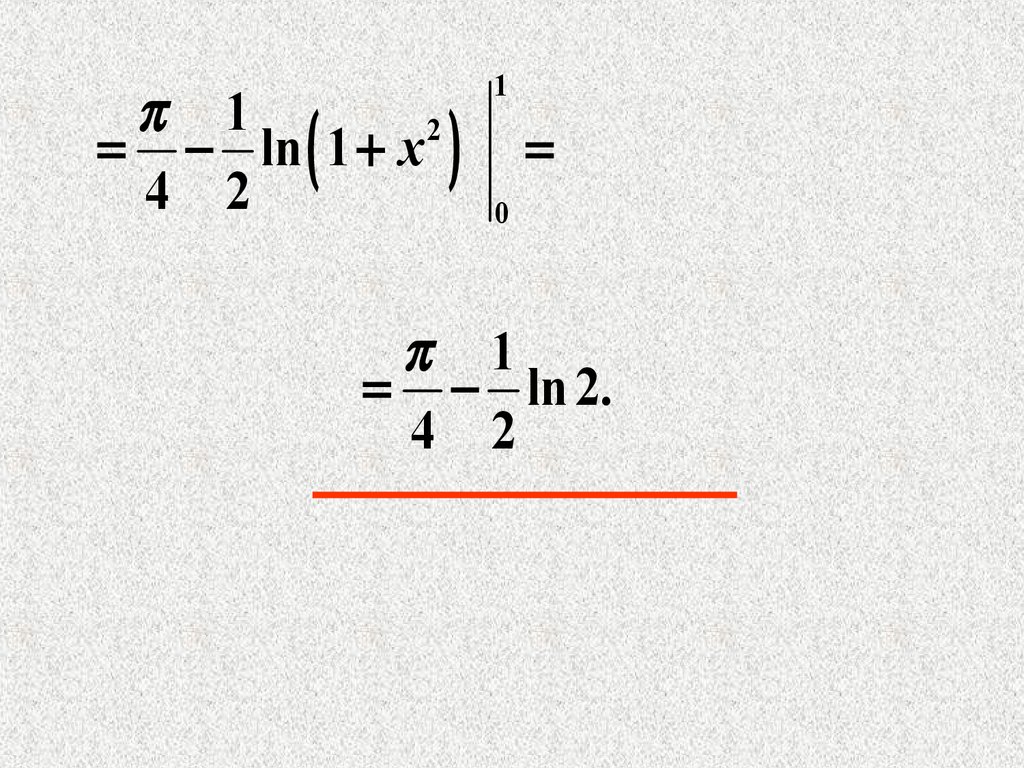
 Математика
Математика








