Статистика, часть 2

1. Статистика, часть 2

Николай Вячеславович Павлов
[email protected]

2. Условные обозначения

Это самое важное, надо знать на 100%!!!
2*2=4
Быть или не быть?
Это надо решить и записать!!!
2

3. АНАЛИЗ ЭМПИРИЧЕСКИХ РАСПРЕДЕЛЕНИЙ

3

4.

Анализ эмпирических распределений = детальное
исследование одномерных массивов данных.
Комплексный анализ рядов распределения включает:
1. Табличное и графическое представление ряда
распределения.
2. Расчет и анализ показателей центра и структуры
распределения.
3. Расчет и анализ показателей вариации.
4. Характеристику формы распределения.
5. Выравнивание эмпирического распределения и
оценку его соответствия тому или иному типу
теоретических распределений.
4

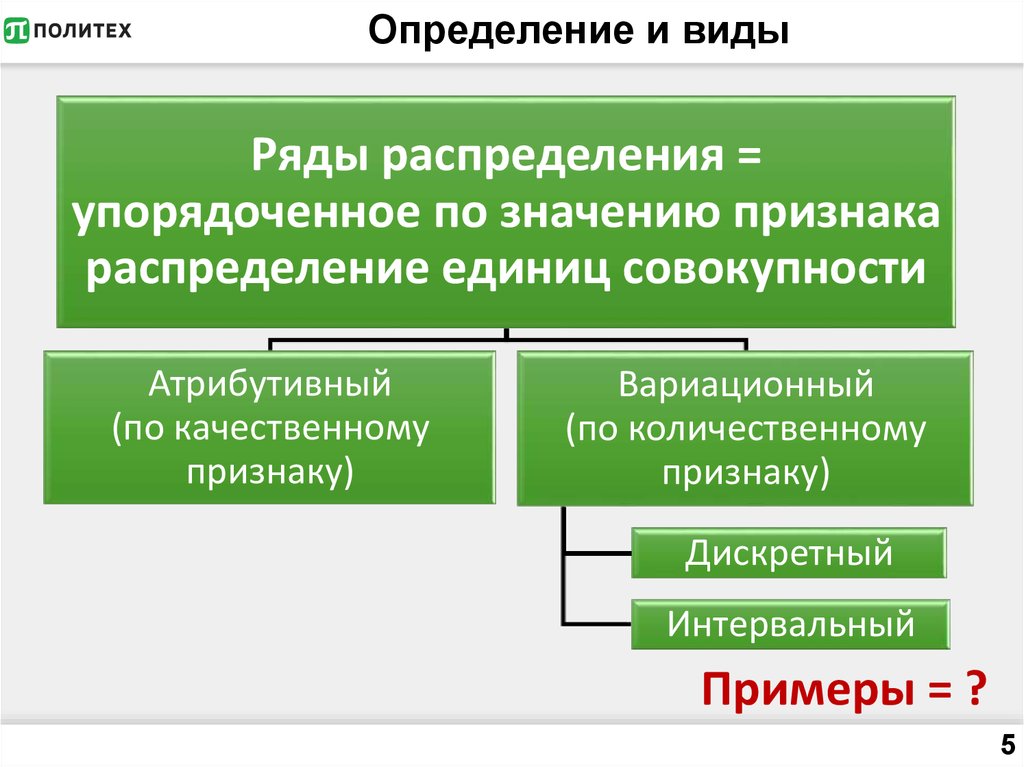
5. Определение и виды

Ряды распределения =
упорядоченное по значению признака
распределение единиц совокупности
Атрибутивный
(по качественному
признаку)
Вариационный
(по количественному
признаку)
Дискретный
Интервальный
Примеры = ?
5

6. Элементы ряда

Варианта
Частота
Ранжирование = упорядочение (Оно есть?)
6

7.

7

8. Ракеты КНДР

8

9. Парк автомобилей

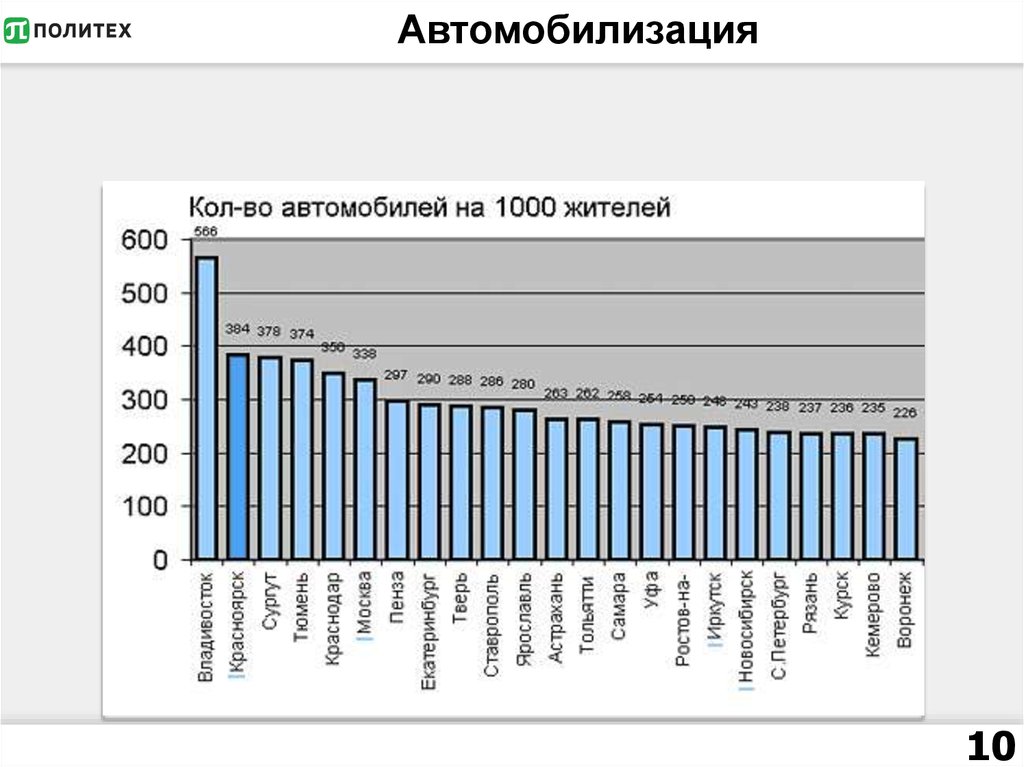
9

10. Автомобилизация

10

11. Показатели центра распределения

11

12. Показатели центра распределения

• Арифметическое среднее значение
• Мода
• Для атрибутивного ряда (категория занятости) = ?
• Для дискретного ряда (размер обуви) = ?
• Для интервального ряда = ?
• Медиана
• Для атрибутивного ряда (уровень образования) = ?
• Для дискретного ряда (размер обуви)= ?
• Для интервального ряда = ?
12

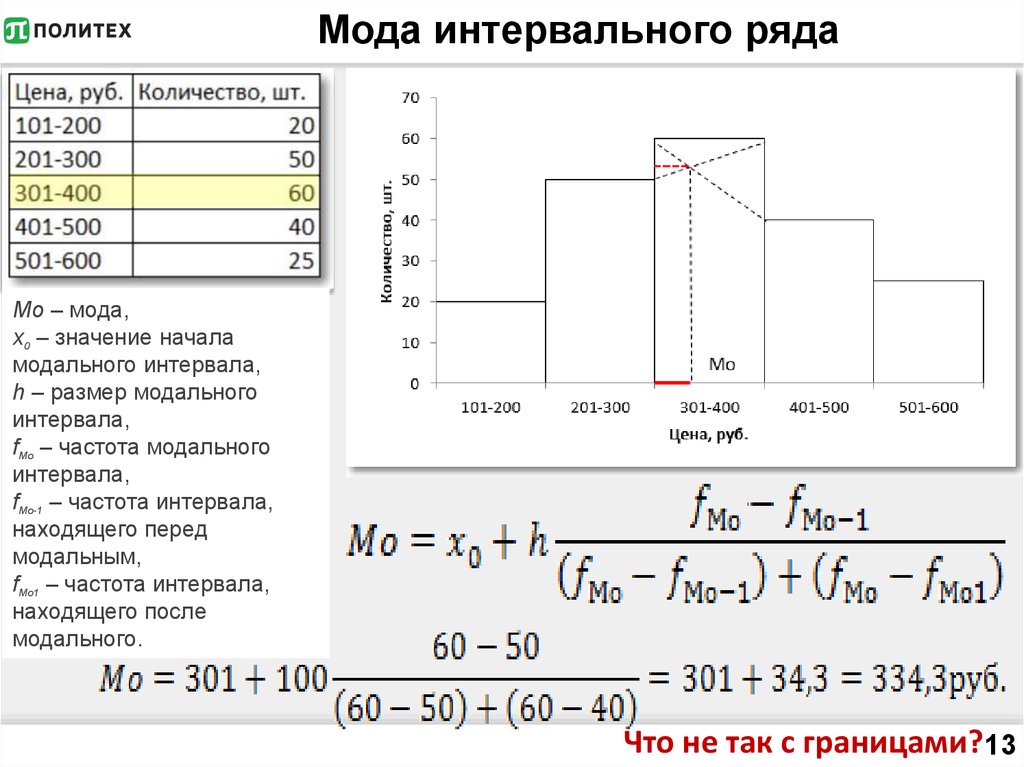
13. Мода интервального ряда

Мо – мода,
x0 – значение начала
модального интервала,
h – размер модального
интервала,
fМо – частота модального
интервала,
fМо-1 – частота интервала,
находящего перед
модальным,
fМо1 – частота интервала,
находящего после
модального.
Что не так с границами?13

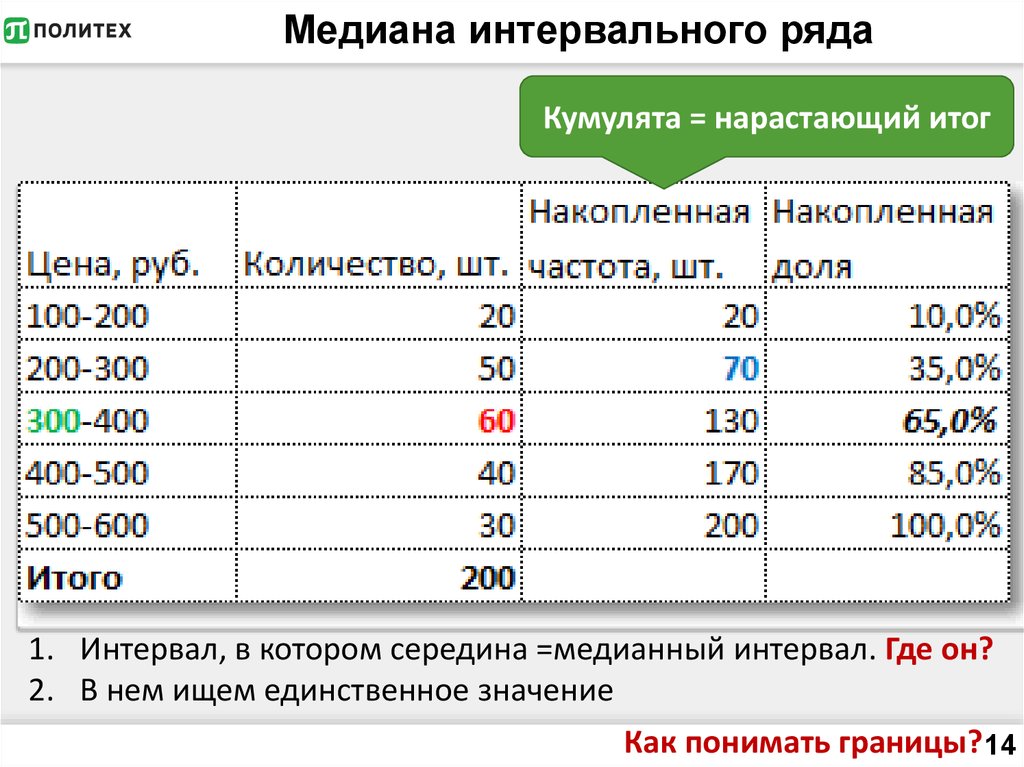
14. Медиана интервального ряда

Кумулята = нарастающий итог
1. Интервал, в котором середина =медианный интервал. Где он?
2. В нем ищем единственное значение
Как понимать границы? 14

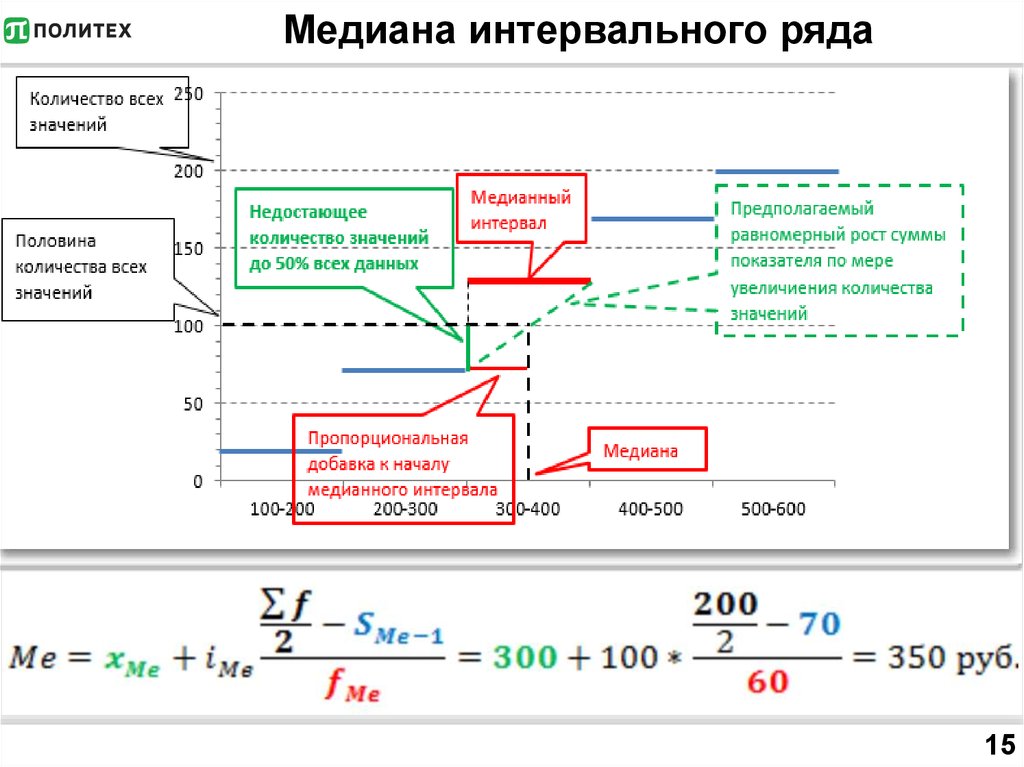
15. Медиана интервального ряда

15

16. Медиана интервального ряда

где
• xMe — нижняя граница медианного интервала;
• iMe — ширина медианного интервала;
• ∑f/2 — количество всех значений, деленное на 2 (два);
• S(Me-1)— суммарное количество наблюдений, которое
было накоплено до начала медианного интервала, т.е.
накопленная частота предмедианного интервала;
• fMe — число наблюдений в медианном интервале.
16

17. Заработная плата в РФ 2016

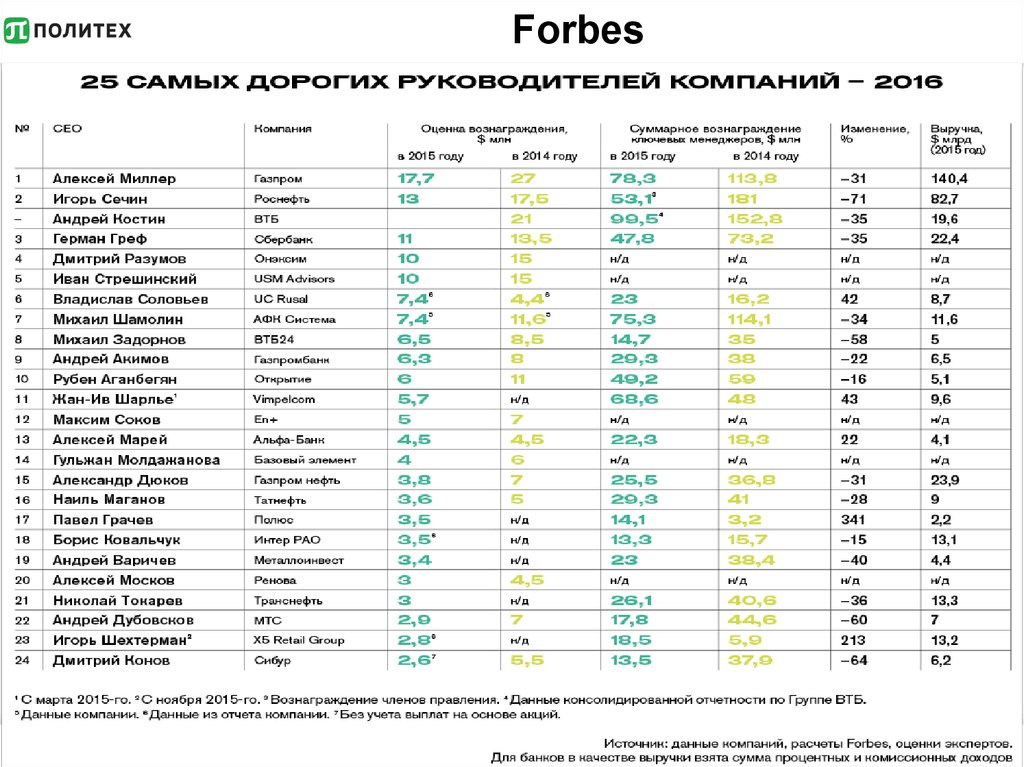
17

18. Forbes

18

19. Показатели структуры распределения

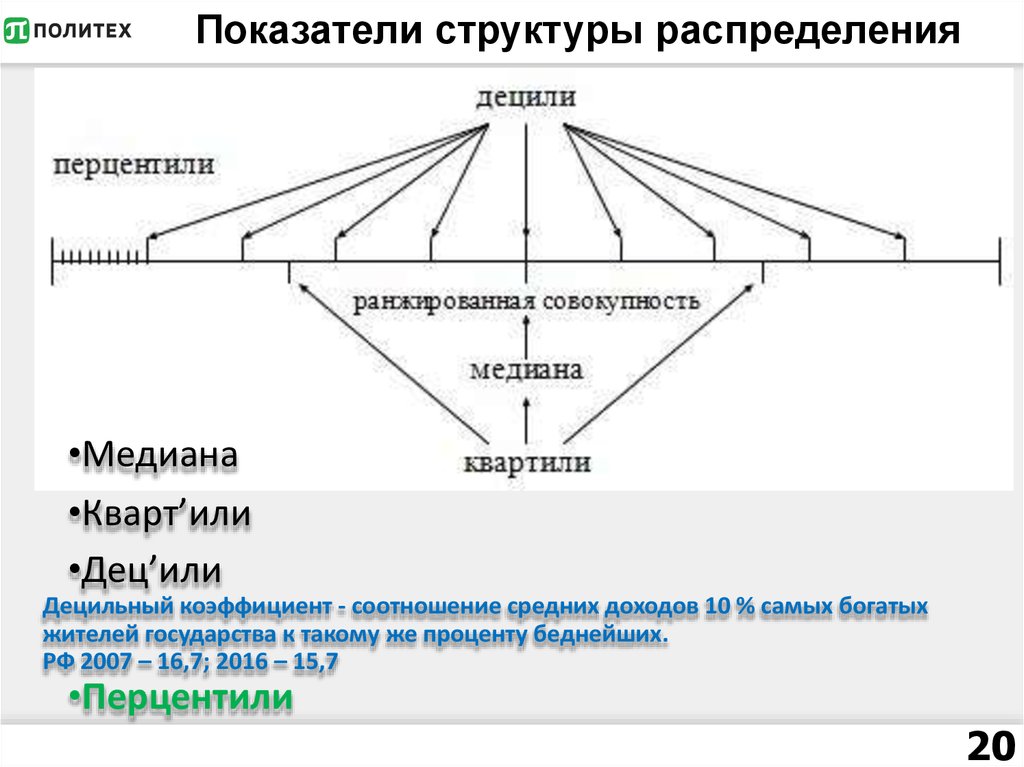
19

20. Показатели структуры распределения

•Медиана
•Кварт’или
•Дец’или
Децильный коэффициент - соотношение средних доходов 10 % самых богатых
жителей государства к такому же проценту беднейших.
РФ 2007 – 16,7; 2016 – 15,7
•Перцентили
20

21. Перцентили

• Это характеристики данных, которые выражают
ранги элементов в виде процентов (от 0 до 100%),
а не в числах.
• Наименьшему значению признака соответствует
нулевой перцентиль, наибольшему – 100-й.
• Перцентили – это показатели, разбивающие
ранжированный ряд данных на определенное
число частей.
21

22. Выбросы

22

23. Было: 10 групп Что это?

Что это?
23

24. Выбросы видны в ранжированном ряду

24

25. Выбросы

• Это единицы совокупности,
значения признака которых
резко отличаются в меньшую
или большую сторону от
основной массы значений
признака.
• Данные единицы
не подчиняются
общей закономерности
распределения, поэтому
анализируются отдельно.
25

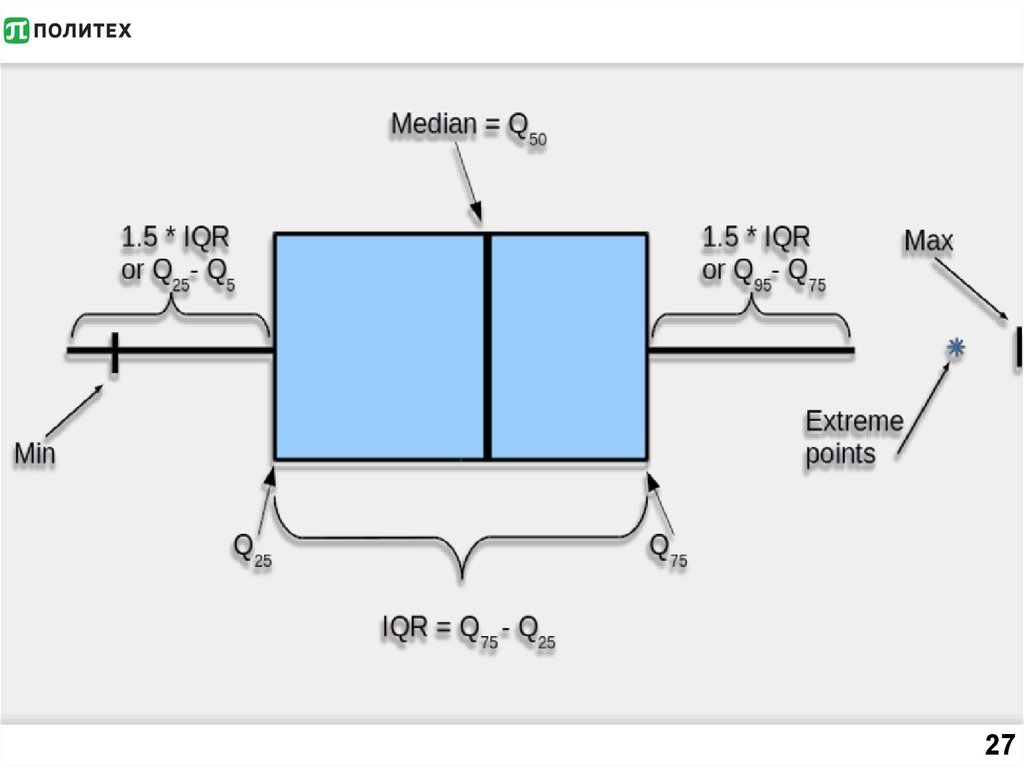
26. Метод Тьюки

• Границы ящика –
1-й (снизу) и 3-й
квартили
• Ширина ящика =
интерквартильный размах
• Ус = полтора
интерквартильных размаха от
ящика
Япония
Ливан
Италия
Эритрея
Португалия
Кабо-Верде
Бутан
Почему медиана
не посередине?
Почему разные
усы???
26

27.

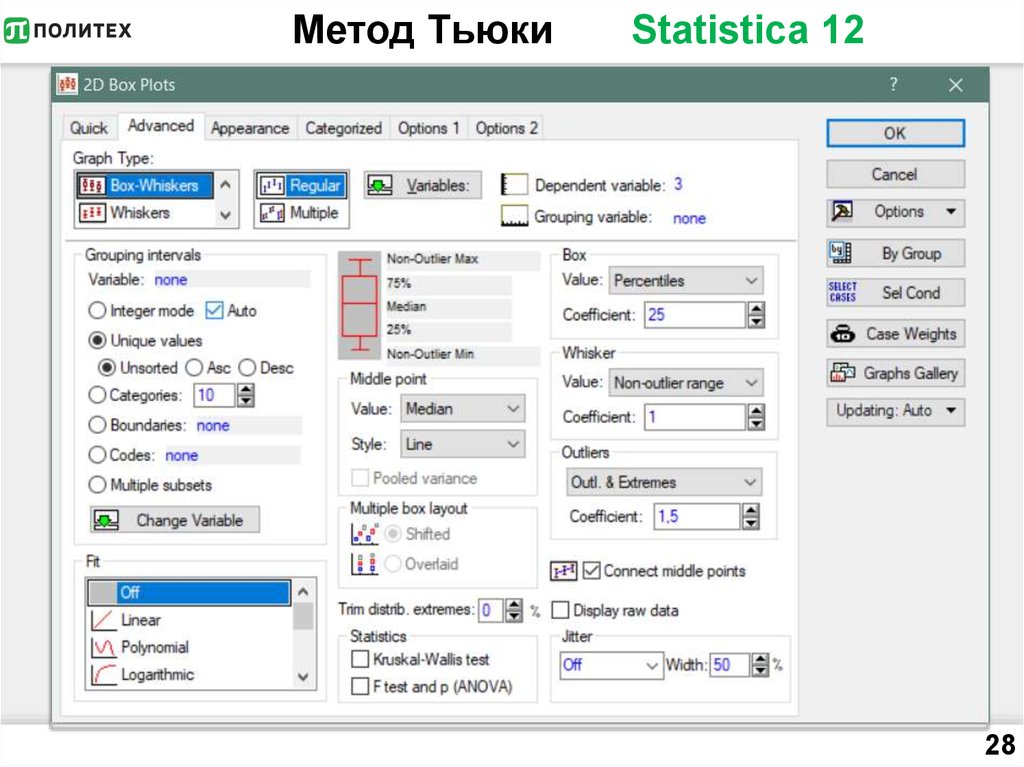
27

28. Метод Тьюки Statistica 12

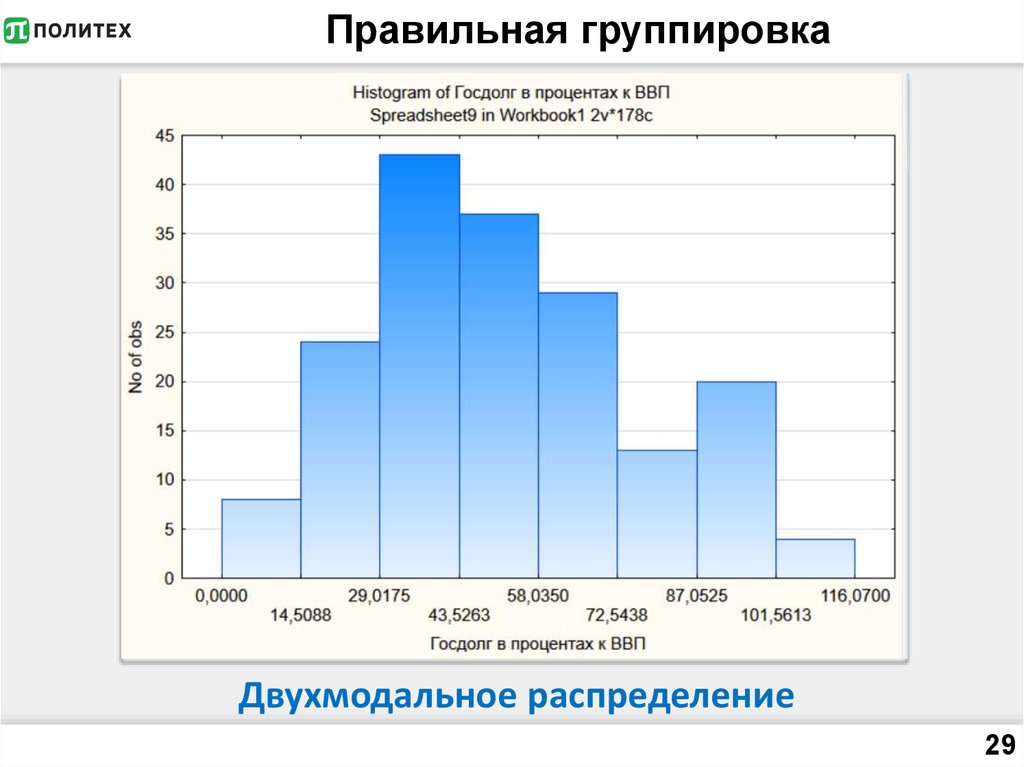
28

29. Правильная группировка

Двухмодальное распределение
29

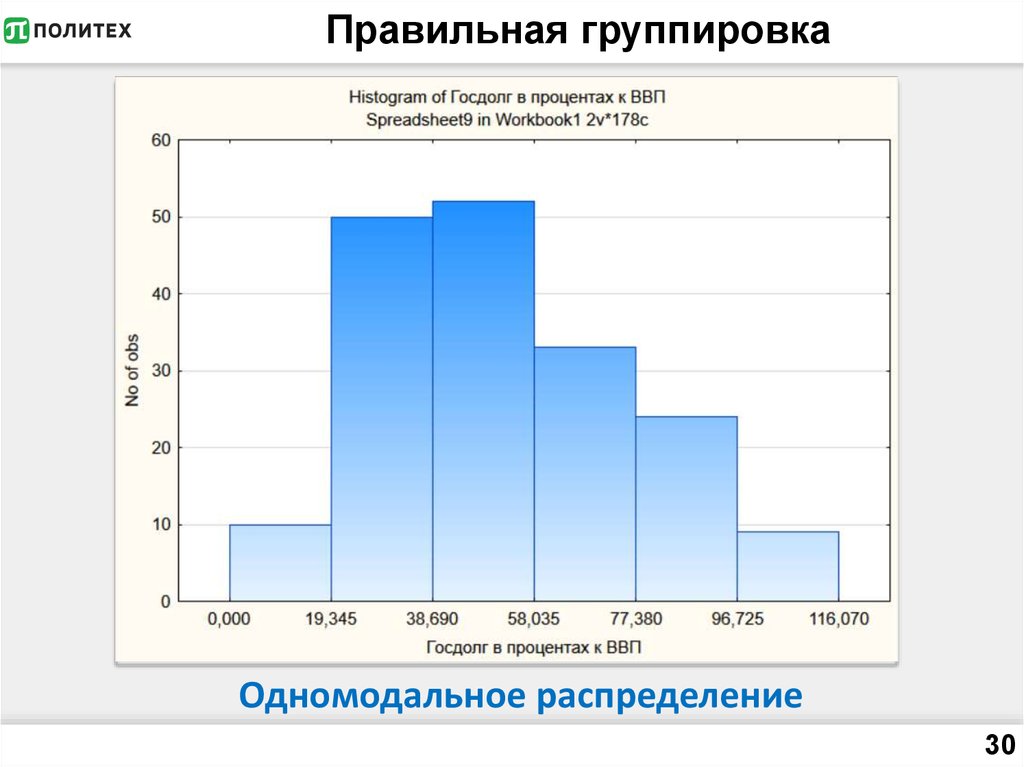
30. Правильная группировка

Одномодальное распределение
30

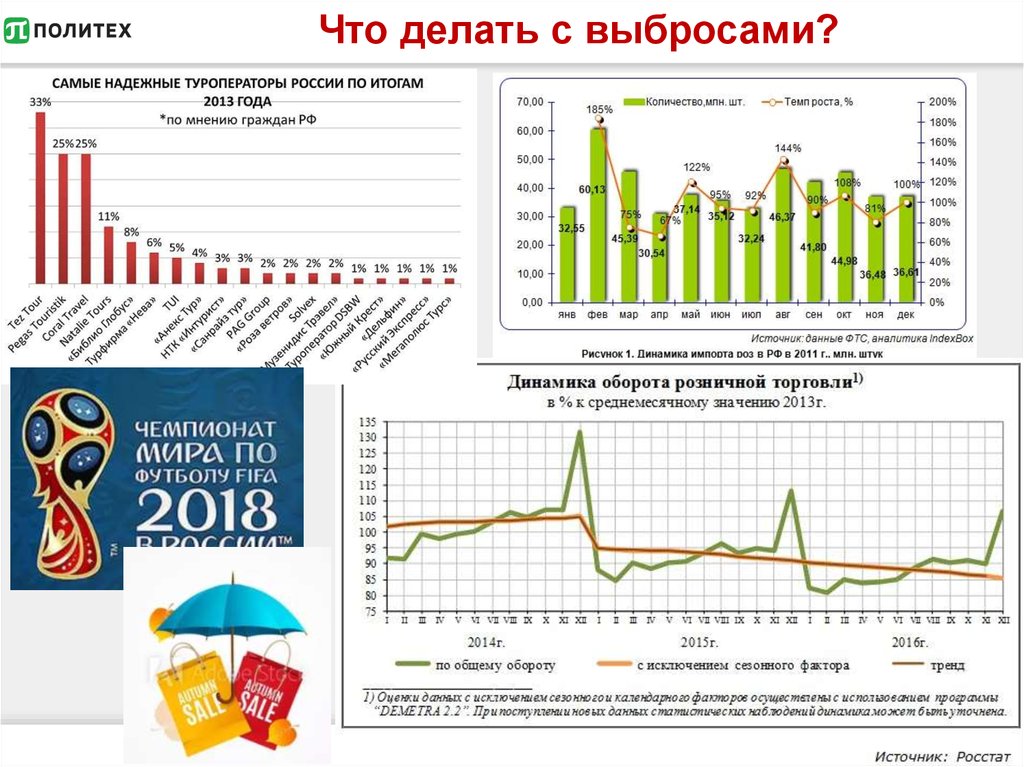
31. Что делать с выбросами?

31

32. Показатели вариации

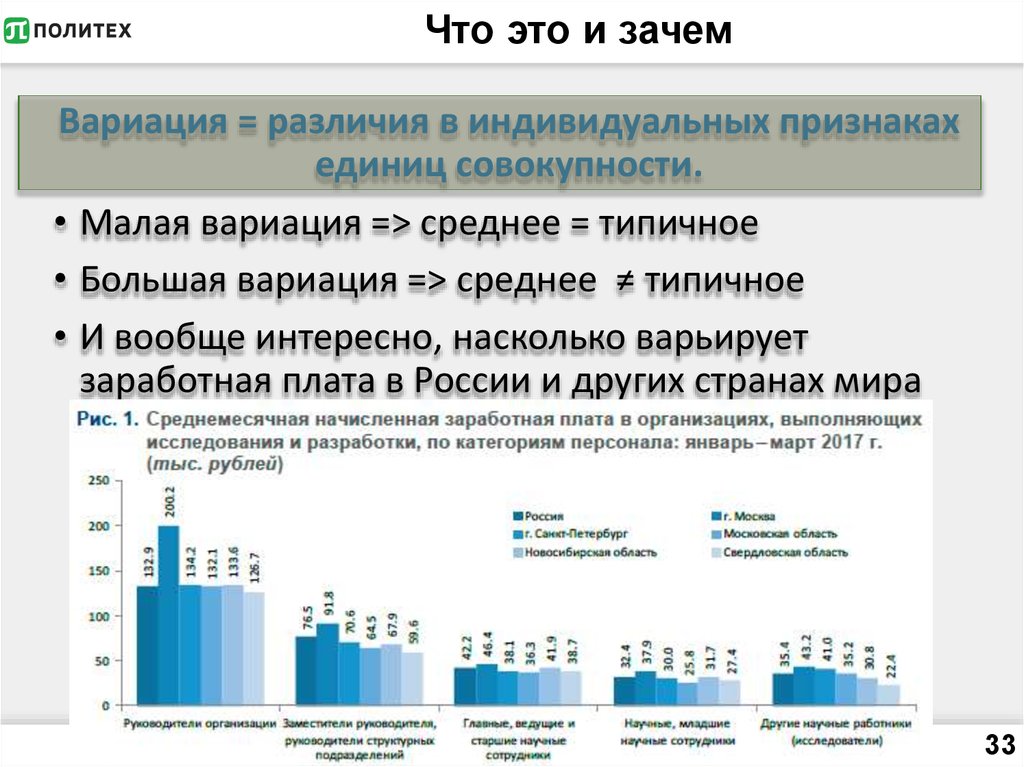
32

33. Что это и зачем

Вариация = различия в индивидуальных признаках
единиц совокупности.
• Малая вариация => среднее = типичное
• Большая вариация => среднее ≠ типичное
• И вообще интересно, насколько варьирует
заработная плата в России и других странах мира
33

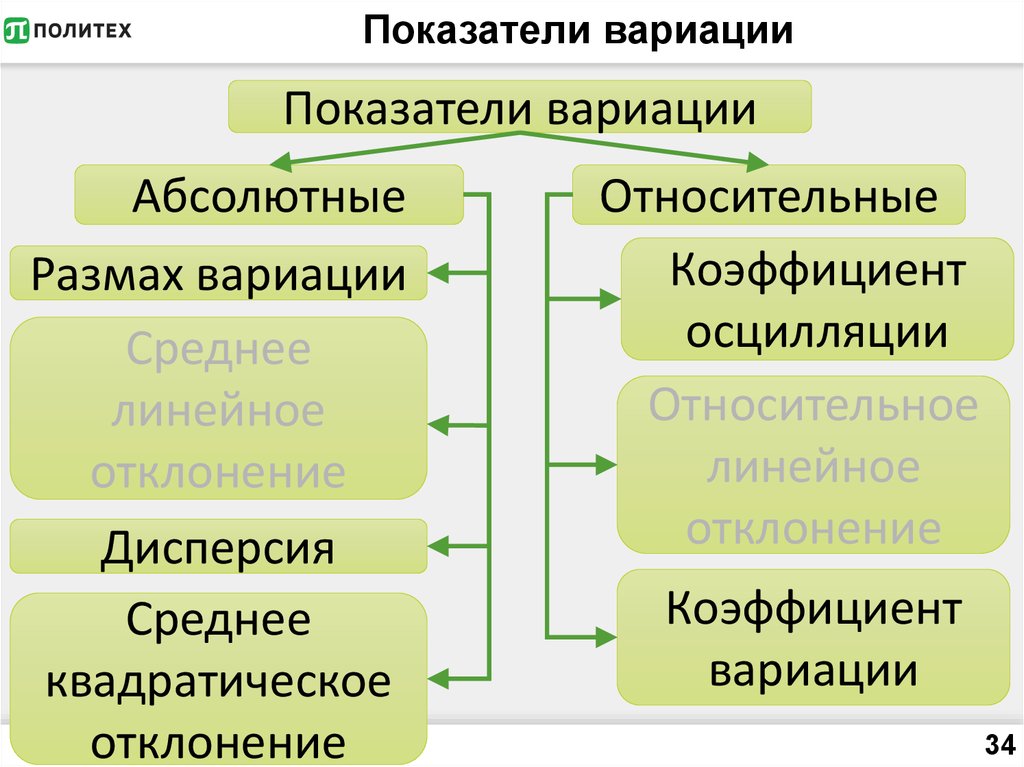
34. Показатели вариации

Показатели вариации
Абсолютные
Размах вариации
Среднее
линейное
отклонение
Дисперсия
Среднее
квадратическое
отклонение
Относительные
Коэффициент
осцилляции
Относительное
линейное
отклонение
Коэффициент
вариации
34

35. Абсолютные показатели вариации

35

36. Размах вариации

R = Xmax - Xmin
Xmax, Xmin – максимальное и минимальное
значения признака в изучаемой совокупности
Зависит от двух измерений, поэтому
неустойчив
Это как так?
Пример: размах зарплаты по СПб

37. Среднее линейное отклонение

x x* f
d
f
i
i
i
x
- среднее значение признака в
совокупности;
x i - индивидуальные значения признака;
f - вес или частота (частость).
i
Формула попроще, без взвешивания = ?
37

38. Дисперсия

2