Похожие презентации:
Загадочный мир фракталов
1.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»
МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ
Загадочный мир фракталов
Выполнил студент 1 курса
группа АТПт-17-9-1
Серёдкин Юрий Евгеньевич
Руководитель: Муштенко Татьяна Петровна
Тюмень, 2018
2.
Содержание проекта•1. История возникновения фракталов
•2. Классификация фракталов и примеры
•3. Практическое применение в жизни
•4. Заключение
•5. Используемая литература
3.
Цель проекта:Познакомиться с миром фракталов и
изучить подробнее эту тему
4.
Задачи проектаИзучить литературу по данной теме
Познакомиться с историей возникновения фракталов
Разобраться в классификации фракталов
Узнать способы практического применения фракталов
в жизни
5.
АктуальностьЗа фракталами будущее. Они точнее передают наш
изменчивый мир, а также с помощью фракталов
можно изучать различные процессы и явления
6.
История фракталовС выходом книги Мандельброта «Фрактальная геоме
трия природы» (The Fractal Geometry of Nature'.) в
1977 году связывают рождение фрактальной геометр
ии.
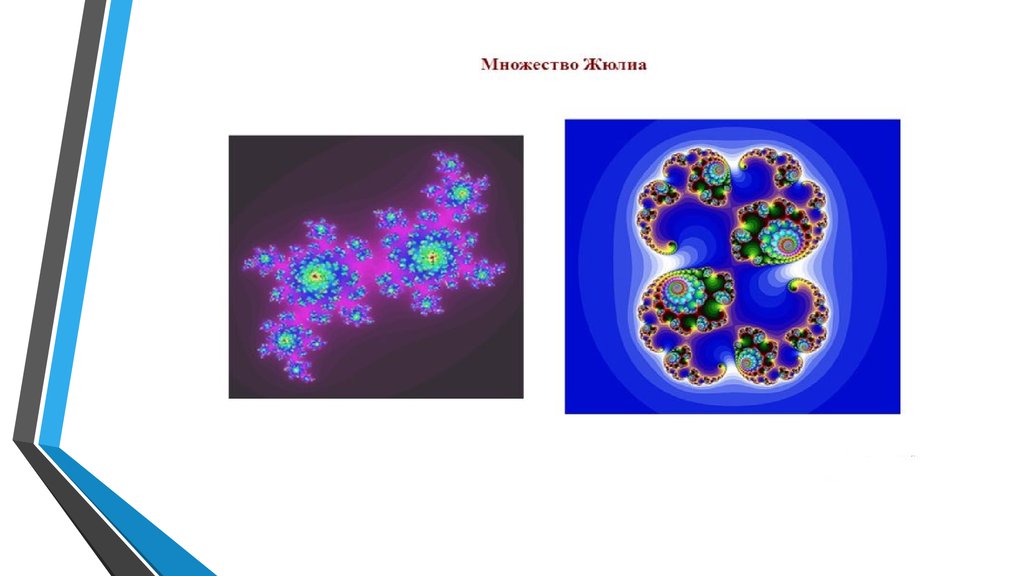
В ней применены научные результаты учёных, среди
них Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф,
работавших
в
период
1875—1925
гг.
в той же области.
И только в наше время
удалось объединить в единую систему эти работы.
Фрактальная геометрия является революцией в матем
атике и математическом описании природы.
7.
История фракталовПонятия «фрактал» и «фрактальная геометрия» появились в 70-80-х годах
XX века. Они устойчиво закрепились в употреблении математиков
и программистов. Слово «фрактал», что в переводе с латинского
означает разбитый, поделённый на части, было предложено Бенуа Мандельброт
ом,французским
математиком, в 1975 году, с целью обозначения нерегулярных самоподобных стр
уктур.
8.
Понятие фракталаФрактал — это
бесконечно самоподобная
геометрическая фигура,
каждый фрагмент которой
повторяется при
уменьшении масштаба.
9.
Бенуа МандельбротСлово «фрактал», что
в переводе с латинского
означает разбитый, поделённый на час
ти,
было предложено Бенуа Мандельброт
ом, французским
математиком, в 1975 году, с целью обо
значения нерегулярных самоподобных
структур.
10.
11.
Алгебраическиефракталы
•Это фракталы
которые можно
построить,
используя простые
алгебраические
формулы
12.
Самым известным примером являетсямножество Мандельброта
13.
Геометрическиефракталы
•Этот тип фракталов
получается
путем
простых
геометрических
построений.
14.
Классическим примером геометрическогофрактала является Снежинка Коха
15.
Стохастическиефракталы
•Они получаются в том
случае, если в итерационном
процессе случайным образом
менять какие-либо его
параметры.
•При этом получаются
объекты очень похожие на
природные - несимметричные
деревья, изрезанные береговые
линии и т.д.
16.
17.
Применение в жизниВ компьютерной графике
фракталы применяются для
построения изображений
природных объектов, таких,
как поверхности морей,
деревья, кусты, горные
ландшафты и т. д.
18.
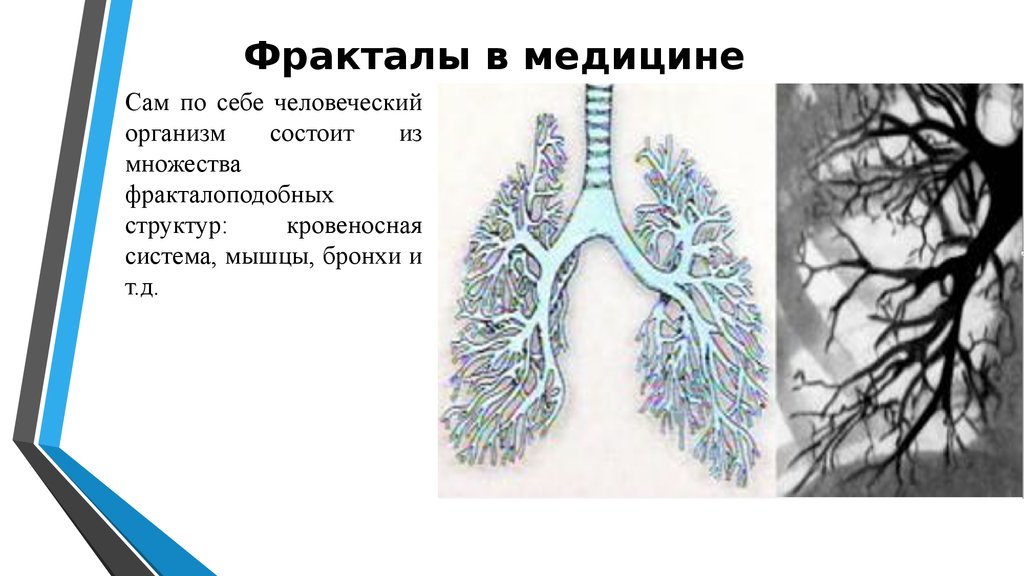
Фракталы в медицинеСам по себе человеческий
организм
состоит
из
множества
фракталоподобных
структур:
кровеносная
система, мышцы, бронхи и
т.д.
19.
ЗаключениеЗнакомясь с историей возникновения фракталов, мы
узнали, что учёные ещё в 19 веке заинтересовались
данной темой, и только в 70-е годы прошлого
столетия появилось понятие фрактал и фрактальная
геометрия. В наши дни практическое применение
фракталов стало незаменимым во многих областях
науки и техники.
20.
Используемая литература1. А. А. Кириллов Повесть о двух фракталах - www.mccme.ru/dubna/2007/notes/kirillov-preprint.pdf. — Летняя
школа «Современная математика». — Дубна, 2007.
2. Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.
3. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.
4. Федер Е. Фракталы. — М: «Мир», 1991.
5. https://ru.wikipedia.org/wiki/Фрактал
6. https://m-rush.ru/theory/item/184-fraktaly-na-praktyke.html
7. https://elementy.ru/posters/fractals/nature
8. http://3dfractal.ru/stati-o-fraktalah/28.html
9. https://ru.wikipedia.org/wiki/Мандельброт,_Бенуа
21.
СПАСИБО ЗАВНИМАНИЕ!



















 Математика
Математика Искусство
Искусство








