Преобразования графиков функций

1. Преобразования графиков функций

Цель презентации: дать теоретическое
обоснование и практический прием
выполнения основных преобразований
графиков функций

2. Пусть y=f(x)- заданная функция. График этой функции может быть подвергнут преобразованиям:

y = f(x)+a
y = f(x+a)
y = - f(x)
y = f(-x)
y = |f(x)|
y = f(|x|)
y = аf(x)
y = f(аx)
комбинации преобразований
Примечание: После рассмотрения каждого из выделенных видов
преобразований Вы можете вернуться на этой слайд,
воспользовавшись гиперссылкой «Возврат».

3.

Заметим, что в уравнении функции y =
f(x)+a «а»- слагаемое при f(x).
Значит: при одном значении аргумента
значение функции y = f(x)+a отличается от
значения функции y= f(x) на «а», то есть:
Если а>0, то значение функции y = f(x)+a
больше значения функции y = f(x) на «a».
Если а<0, то значение функции y = f(x)+a
меньше значения функции y = f(x) на «|a|».
Взаимное расположение графиков в
выделенных случаях проиллюстрировано на
Рис.1.

4.

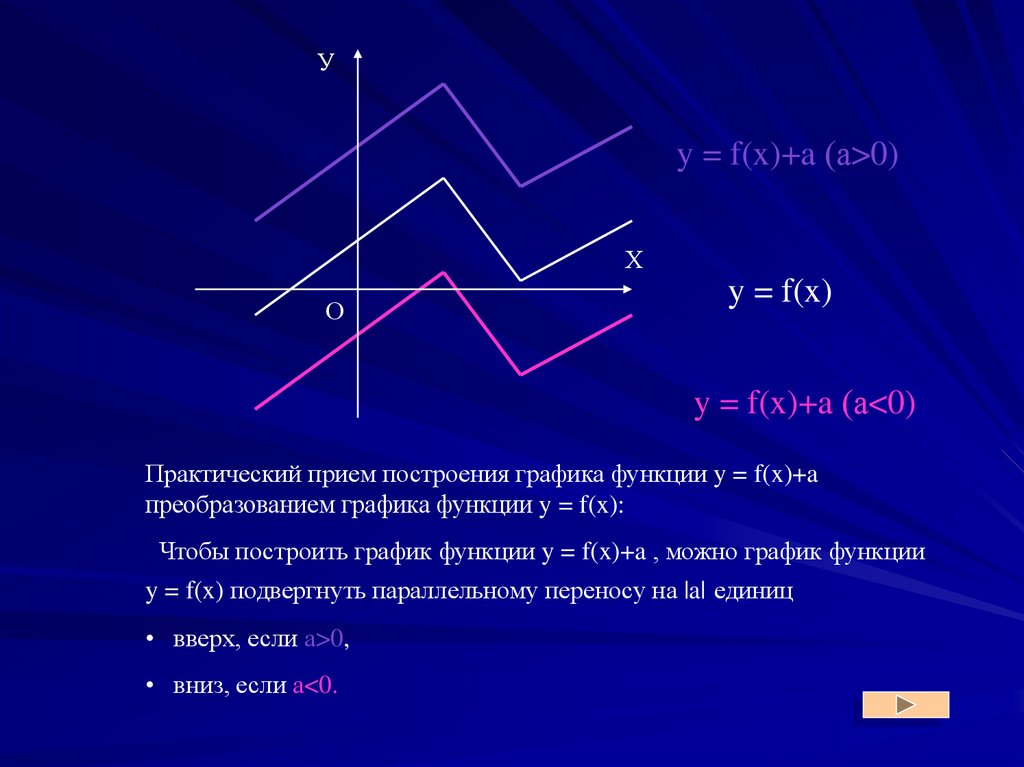
У
y = f(x)+a (а>0)
Х
О
y = f(x)
y = f(x)+a (а<0)
Практический прием построения графика функции y = f(x)+a
преобразованием графика функции y = f(x):
Чтобы построить график функции y = f(x)+a , можно график функции
y = f(x) подвергнуть параллельному переносу на |a| единиц
• вверх, если а>0,
• вниз, если а<0.

5.

Элементы самоконтроля (правильности построения графика):
Аналитическим путем
• найти область определения функции и сопоставить с соответствующим
свойством графика;
• найти множество значений функции и сопоставить с соответствующим
свойством графика;
• найти корни функции и сравнить их с абсциссами (абсциссой) точек
пересечения графика с осью абсцисс;
• найти ординату точки пересечения графика функции с осью ординат и
сравнить с соответствующей характеристикой точки графика
Замечание:
• если график основной функции y = f(x) имеет асимптоты, то и
результатирующий график, полученный в результате преобразования
(композиции преобразований) также имеет асимптоты.

6.

1. Сравнивая уравнения функций y = f(x) и y = f(x+a), заметим, что «a» слагаемое при аргументе.
2. Чтобы установить взаимное расположение графиков выделенных
функций, выясним взаимосвязь аргументов этих функций при равных
значениях функций.
3. Пусть (х0,y0) – координаты точки графика y=f(x), а (х1,y0) – координаты
соответствующей точки графика функции y=f(x+а).
То есть верны равенства: y0= f(х0), y0= f(х1 +а).
Отсюда верно равенство: х0= х1 +а
или
х1 = х0- а
Последнее равенство говорит о том, что:
# если а 0, то х1 х0 на « а »,
#
если а 0, то х1 х0 на « а ».

7.

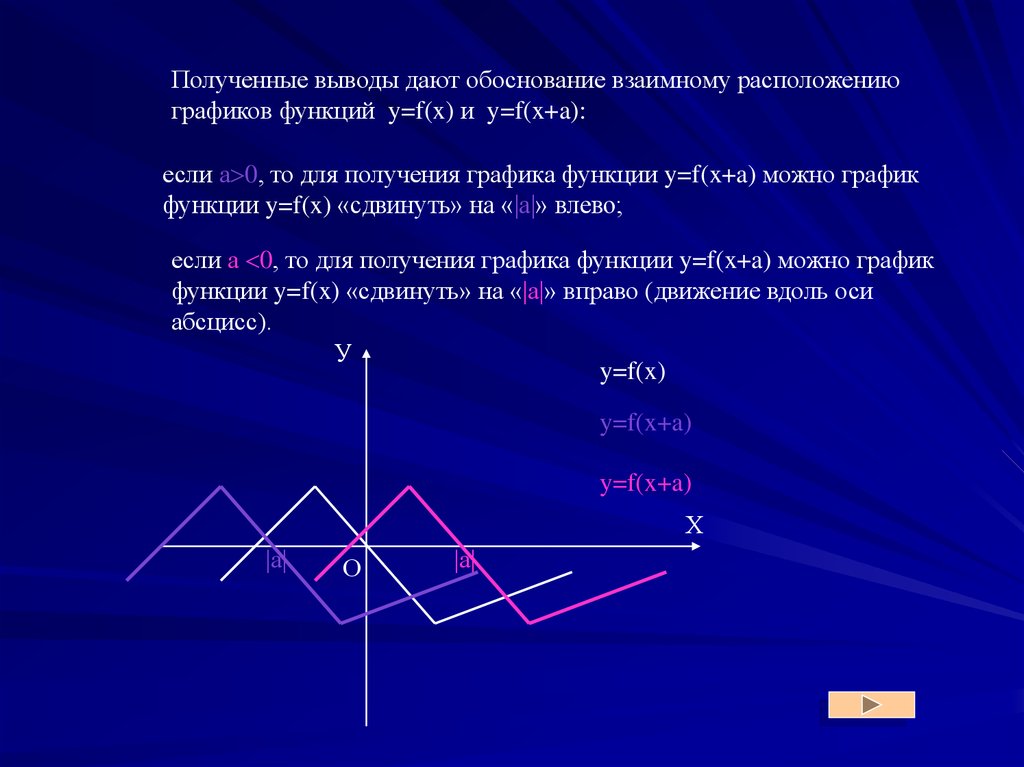
Полученные выводы дают обоснование взаимному расположению
графиков функций y=f(x) и y=f(x+a):
если а 0, то для получения графика функции y=f(x+a) можно график
функции y=f(x) «сдвинуть» на « а » влево;
если а 0, то для получения графика функции y=f(x+a) можно график
функции y=f(x) «сдвинуть» на « а » вправо (движение вдоль оси
абсцисс).
У
y=f(x)
y=f(x+a)
y=f(x+a)
Х
а
О
а

8.

Уравнение функции y = - f(x) можно привести к виду y = (-1)f(x).
Не трудно заметить, что при одном значении аргумента значение
функции y = - f(x) противоположно значению функции y= f(x).
Это означает, что если точка с координатами (х0,y0) – точка графика y=f(x),
то точка с координатами (х0,- y0) – точка графика y= - f(x).
По свойству взаимного расположения точек координатной плоскости:
точки с равными абсциссами и противоположными ординатами
симметричны относительно оси абсцисс.
Вывод: График функции y = - f(x) можно получить из графика функции
y = f(x), выполнив преобразование «осевая симметрия относительно оси
абсцисс».
Взаимное расположение графиков продемонстрировано на Рис.3

9.

У
y = f(x)
Х
О
y = - f(x)
При выполнении симметрии относительно оси абсцисс целесообразно
помнить:
отрезки переходят в равные отрезки, прямые – в прямые, кривые – в
равные им кривые;
характеристические точки основного графика переходят в
симметричные им точки относительно оси абсцисс;
точки пересечения основного графика с осью абсцисс отображаются
на себя (остаются на месте)
если мысленно перегнуть плоскость по оси абсцисс, графики
функций «наложатся» друг на друга

10.

1. Чтобы установить взаимное расположение графиков выделенных
функций, выясним взаимосвязь аргументов этих функций при
равных значениях функций.
2. Сравнивая уравнения функций y = f(- x) и y = f(x), заметим, что
аргументы противоположны.
3. Пусть (х0,y0) – координаты точки графика y=f(x), а (х1,y0) –
координаты соответствующей точки графика функции y=f(- x).
То есть верны равенства: y0=f(х0), y0=f(х1). Отсюда верно
равенство: х0= - х1 или
х1 = - х0
Вывод: Если аргументы функций противоположны, то значения
функций равны.

11.

4.
Геометрической интерпретацией полученного вывода
является утверждение: если точка с координатами
(х0,y0) – точка графика y=f(x), то точка с координатами
(- х0, y0) – точка графика y= f(- x).
5.
По свойству взаимного расположения точек
координатной плоскости: точки с противоположными
абсциссами и равными ординатами симметричны
относительно оси ординат.
Вывод: График функции y = f(- x) можно получить из
графика функции y = f(x), выполнив преобразование
«осевая симметрия относительно оси ординат».
Взаимное расположение графиков продемонстрировано на
Рис.4

12.

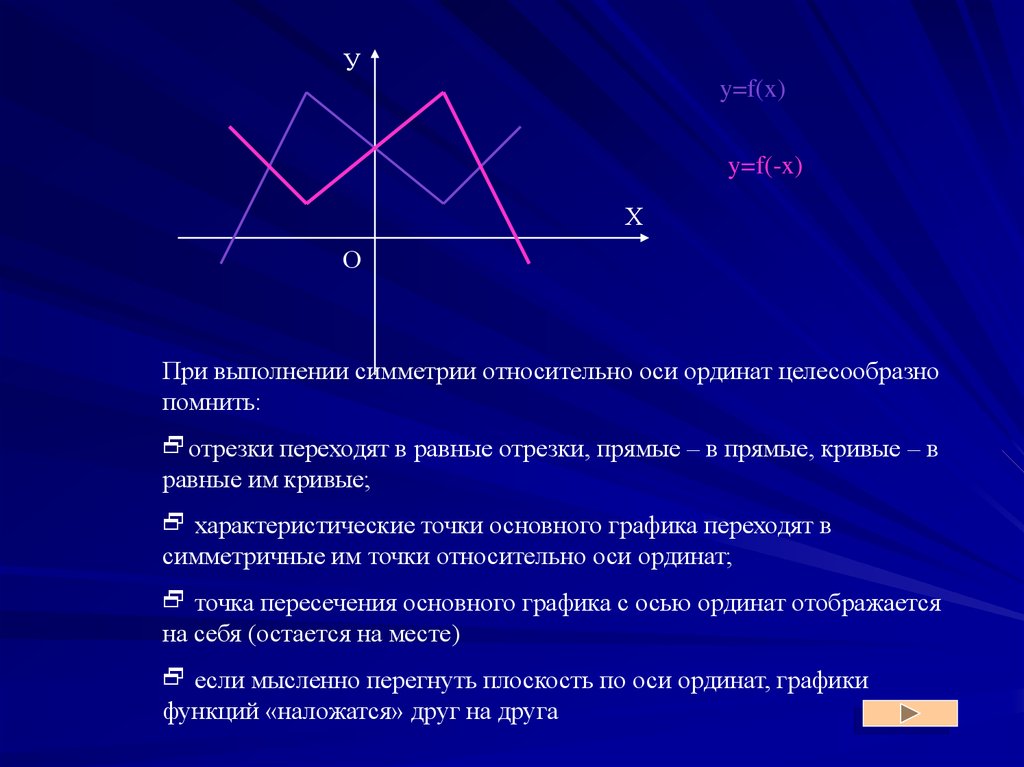
У
y=f(x)
y=f(-x)
Х
О
При выполнении симметрии относительно оси ординат целесообразно
помнить:
отрезки переходят в равные отрезки, прямые – в прямые, кривые – в
равные им кривые;
характеристические точки основного графика переходят в
симметричные им точки относительно оси ординат;
точка пересечения основного графика с осью ординат отображается
на себя (остается на месте)
если мысленно перегнуть плоскость по оси ординат, графики
функций «наложатся» друг на друга

13.

Уравнение функции y=|f(x)| можно записать в виде:
f(x), если f(x) 0
y=
- f(x), если f(x) <0
Значит, для построения графика функции y=|f(x)|, можно в одной системе
координат построить графики функций y=f(x) (основной график) и y=- f(x)
(симметрия основного графика относительно оси абсцисс).
Графиком функции y=|f(x)| будет объединение множеств точек:
• графика функции y=f(x) на том множестве области определения, на
котором f(x) 0,
• графика функции y=- f(x) на том множестве области определения, на
котором f(x)<0.
Этапы построения графиков выделены на Рис.5-6.

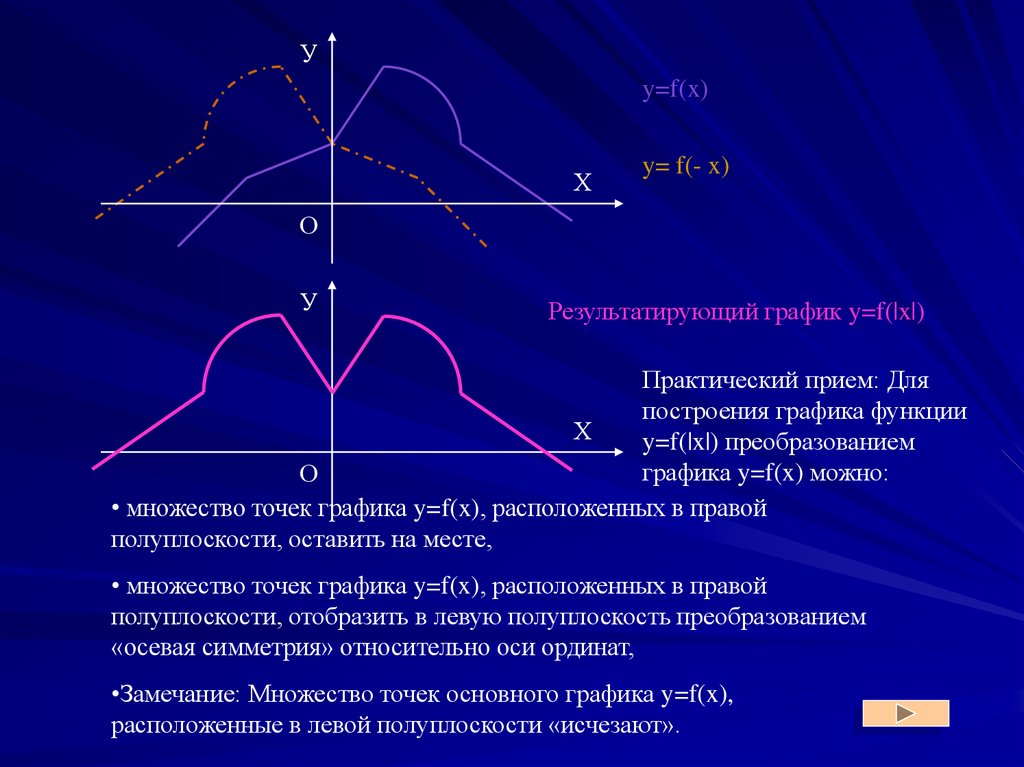
14.

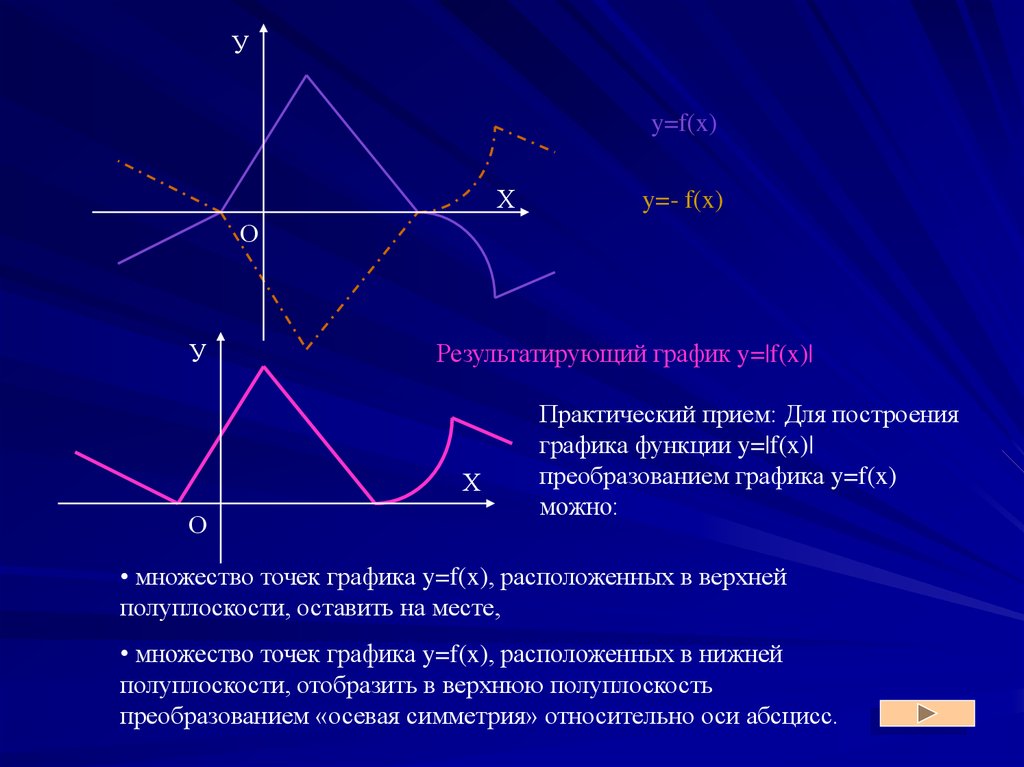
У
y=f(x)
Х
y=- f(x)
О
У
Результатирующий график y=|f(x)|
Х
О
Практический прием: Для построения
графика функции y=|f(x)|
преобразованием графика y=f(x)
можно:
• множество точек графика y=f(x), расположенных в верхней
полуплоскости, оставить на месте,
• множество точек графика y=f(x), расположенных в нижней
полуплоскости, отобразить в верхнюю полуплоскость
преобразованием «осевая симметрия» относительно оси абсцисс.

15.

Уравнение функции y=f(|x|) можно записать в виде:
f(x), если x 0
y=
f(-x), если x < 0
Значит, для построения графика функции y=f(|x|) можно в одной системе
координат построить графики функций y=f(x) (основной график) и y=f(-x)
(симметрия основного графика относительно оси ординат).
Графиком функции y=f(|x|) будет объединение множеств точек:
• графика функции y=f(x) на том множестве области определения, на
котором x 0,
• графика функции y= f(-x) на том множестве области определения, на
котором x <0.
Этапы построения графиков выделены на Рис.7-8.

16.

У
y=f(x)
Х
y= f(- x)
О
У
Результатирующий график y=f(|x|)
Практический прием: Для
построения графика функции
Х
y=f(|x|) преобразованием
графика y=f(x) можно:
О
• множество точек графика y=f(x), расположенных в правой
полуплоскости, оставить на месте,
• множество точек графика y=f(x), расположенных в правой
полуплоскости, отобразить в левую полуплоскость преобразованием
«осевая симметрия» относительно оси ординат,
•Замечание: Множество точек основного графика y=f(x),
расположенные в левой полуплоскости «исчезают».

17.

Преобразование у=af(x) рассмотрим при а>0, выделяя случаи: 0<а<1 и а >1.
Замечание: Если а<0, то график функции у=af(x) можно построить
подвергнув график функции y=f(x) композиции преобразований y=-f(x) и
у=af(x) при а>0.
Заметим, что в уравнении функции y = аf(x) «а»- сомножитель при f(x).
Значит: при одном значении аргумента модуль значения функции y = аf(x)
равен произведению модуля значения функции y= f(x) и «а», то есть:
Если 0<а<1 , то модуль значения функции y = аf(x) меньше модуля
значения функции y = f(x).
Если а >1, то модуль значения функции y = аf(x) больше модуля
значения функции y = f(x).
Дадим иллюстрацию взаимного расположения графиков в выделенных
случаях при а=1/2 (Рис.9) и а=2 (Рис.10).

18.

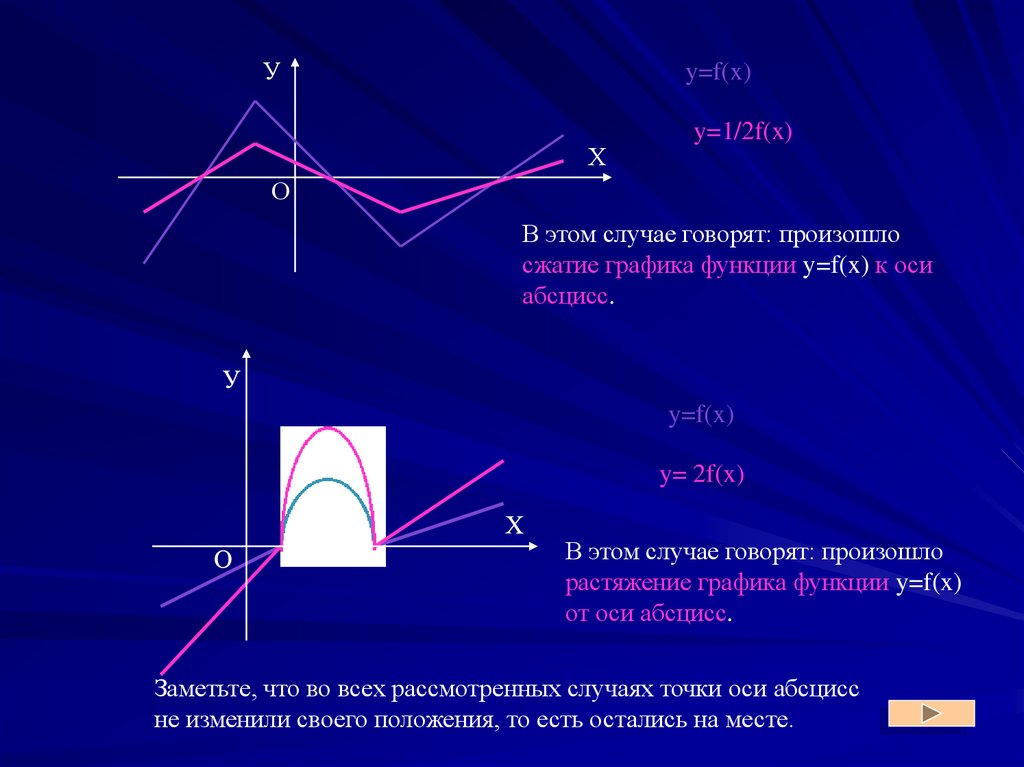
У
y=f(x)
Х
y=1/2f(x)
О
В этом случае говорят: произошло
сжатие графика функции y=f(x) к оси
абсцисс.
y=f(x)
y= 2f(x)
В этом случае говорят: произошло
растяжение графика функции y=f(x)
от оси абсцисс.
Заметьте, что во всех рассмотренных случаях точки оси абсцисс
не изменили своего положения, то есть остались на месте.

19.

Преобразование у=f(аx) рассмотрим при а>0, выделяя случаи: 0<а<1 и а >1.
Замечание: Если а<0, то график функции у=f(аx) можно построить
подвергнув график функции y=f(x) композиции преобразований y=f(-x) и
у=f(аx) при а>0.
Чтобы установить взаимное расположение графиков выделенных функций,
выясним взаимосвязь аргументов этих функций при равных значениях
функций.
Пусть (х0,y0) – координаты точки графика y=f(x), а (х1,y0) – координаты
соответствующей точки графика функции y=f(аx).
То есть верны равенства: y0=f(х0), y0=f(ах1). Отсюда верно равенство: х0=ах1
или
х1 =1/а х0
Последнее равенство позволяет сделать следующие выводы:
1. Если 0<а<1, то (1/а )>1, то есть |х1 | > | х0 | в (1/а) раз.

20.

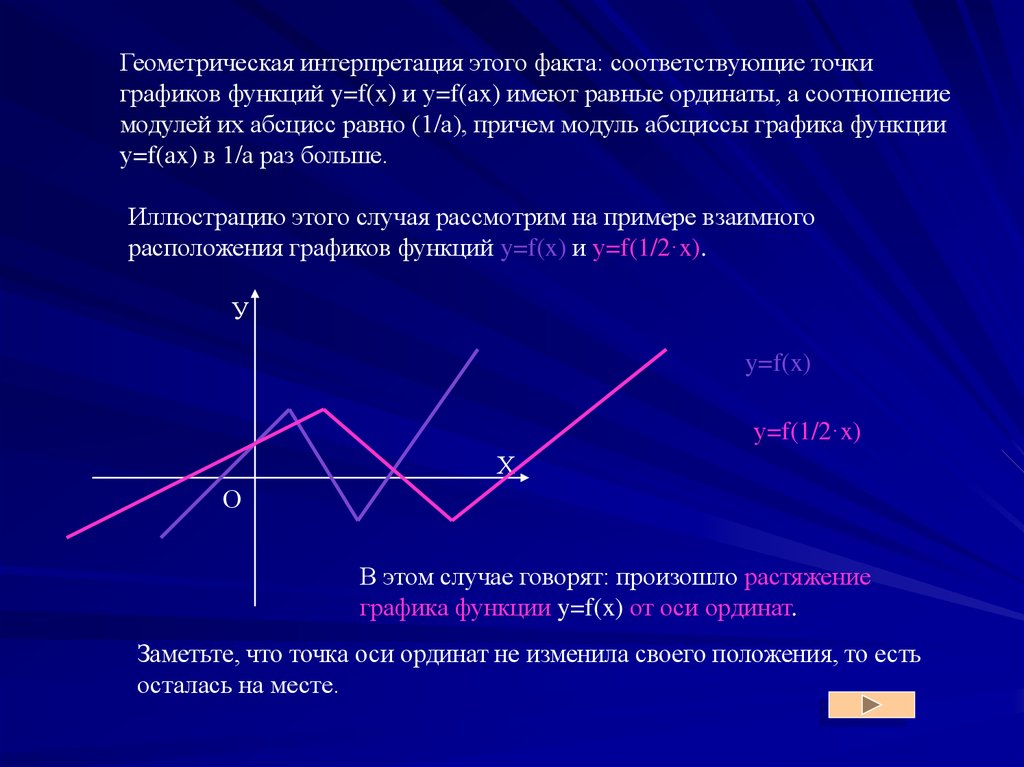
Геометрическая интерпретация этого факта: соответствующие точки
графиков функций y=f(x) и у=f(аx) имеют равные ординаты, а соотношение
модулей их абсцисс равно (1/а), причем модуль абсциссы графика функции
у=f(аx) в 1/а раз больше.
Иллюстрацию этого случая рассмотрим на примере взаимного
расположения графиков функций y=f(x) и у=f(1/2·x).
У
y=f(x)
у=f(1/2·x)
Х
О
В этом случае говорят: произошло растяжение
графика функции y=f(x) от оси ординат.
Заметьте, что точка оси ординат не изменила своего положения, то есть
осталась на месте.

21.

2. Если а>1, то (1/а ) <1, то есть |х1 | < | х0 | в (а) раз.
Геометрическая интерпретация этого факта: соответствующие точки
графиков функций y=f(x) и у=f(аx) имеют равные ординаты, а
соотношение модулей их абсцисс равно (1/а), причем модуль абсциссы
графика функции у=f(аx) в (а) раз меньше.
Иллюстрацию этого случая рассмотрим на примере взаимного
расположения графиков функций y=f(x) и у=f(2·x).
У
y=f(x)
у=f(2·x)
Х
О
В этом случае говорят:
произошло сжатие графика
функции y=f(x) к оси ординат.
Заметьте, что точка оси ординат не изменила
своего положения, то есть осталась на месте.

22.

y=f(x) y=|f(x)| Преобразование y=f(|x|)
y=f(|x|) у=af(x) Преобразование у=af(x)
y=f(ax) Преобразование y=f(ax)

23.

24.

У
Х
О

25.

У
Х
О

26.

У
Х
О