Преобразования графиков функций

1. Преобразования графиков функций

Презентацию выполнила
Кислова Алина

2. Содержание:

1. Основные функции и их графики
2. Основные приемы преобразований
графиков

3. Основные функции и их графики:

линейная функция;
обратная пропорциональность;
квадратичная функция;
у=х3;
у= х.

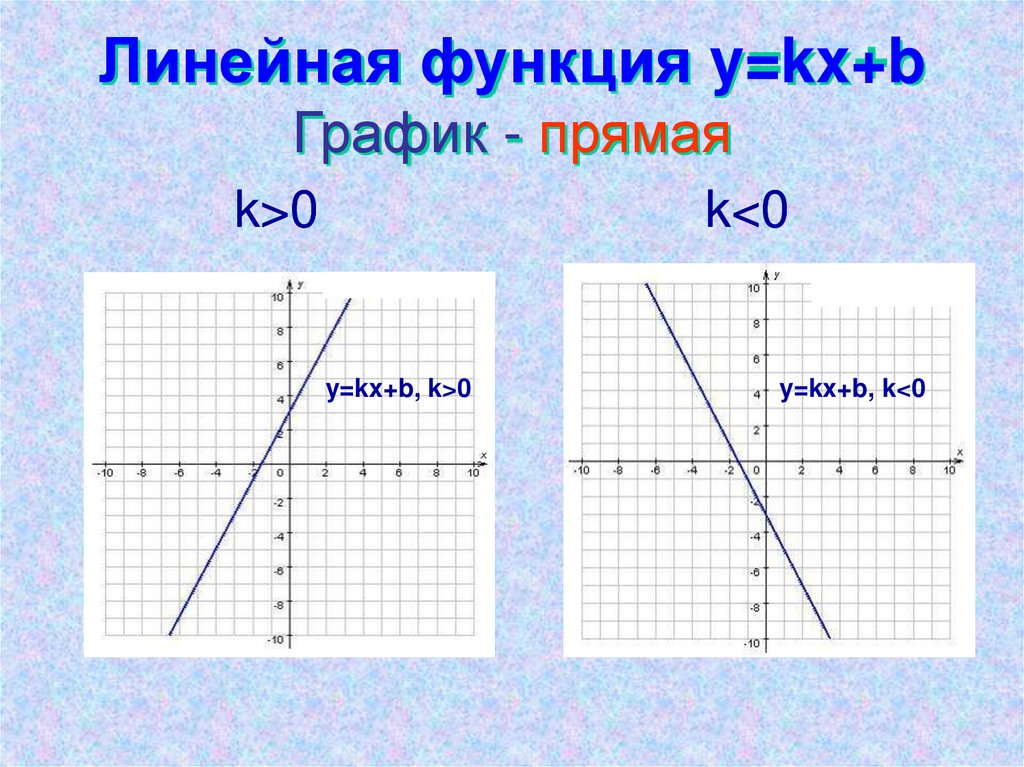
4. Линейная функция y=kx+b График - прямая

k>0
k<0
y=kx+b, k>0
y=kx+b, k<0

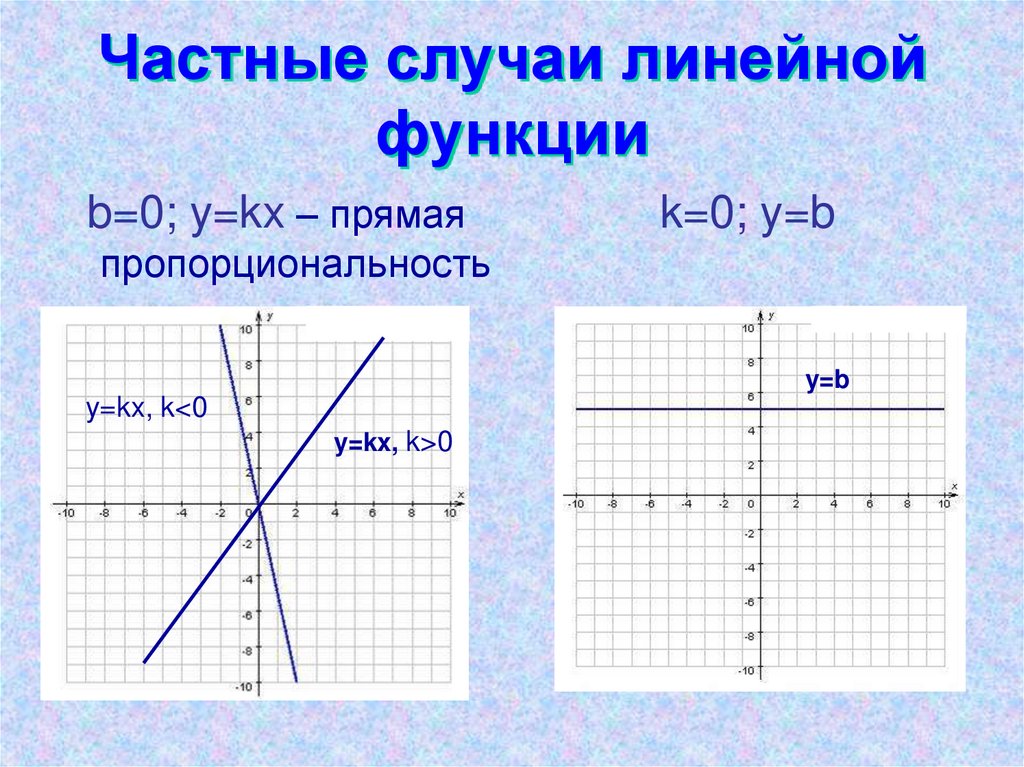
5. Частные случаи линейной функции

b=0; y=kx – прямая
k=0; y=b
пропорциональность
y=b
y=kx, k<0
y=kx, k>0

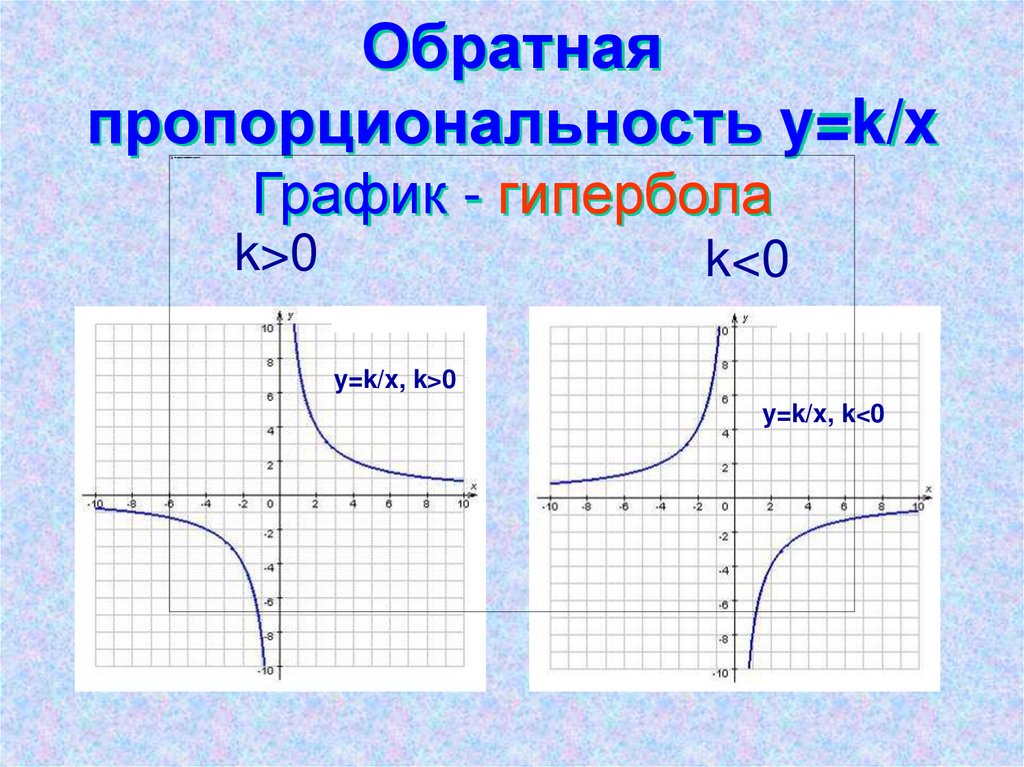
6. Обратная пропорциональность y=k/x График - гипербола

k>0
k<0
y=k/x, k>0
y=k/x, k<0

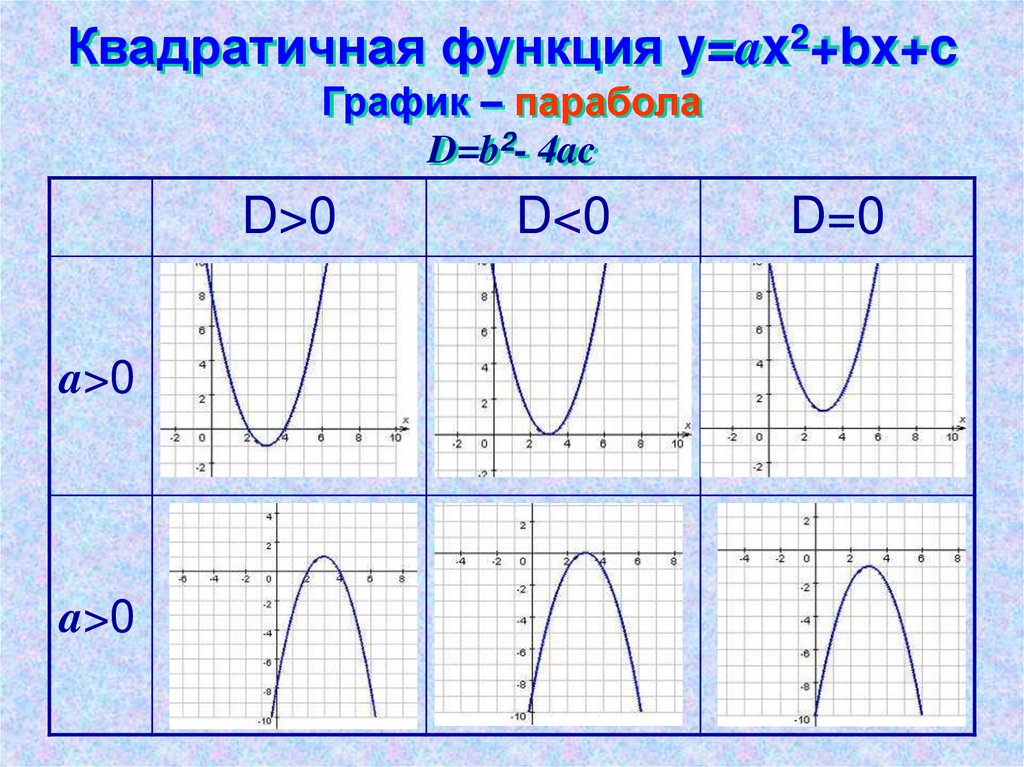
7. Квадратичная функция y=ax2+bx+c График – парабола D=b2- 4ac

D>0
a>0
a>0
D<0
D=0

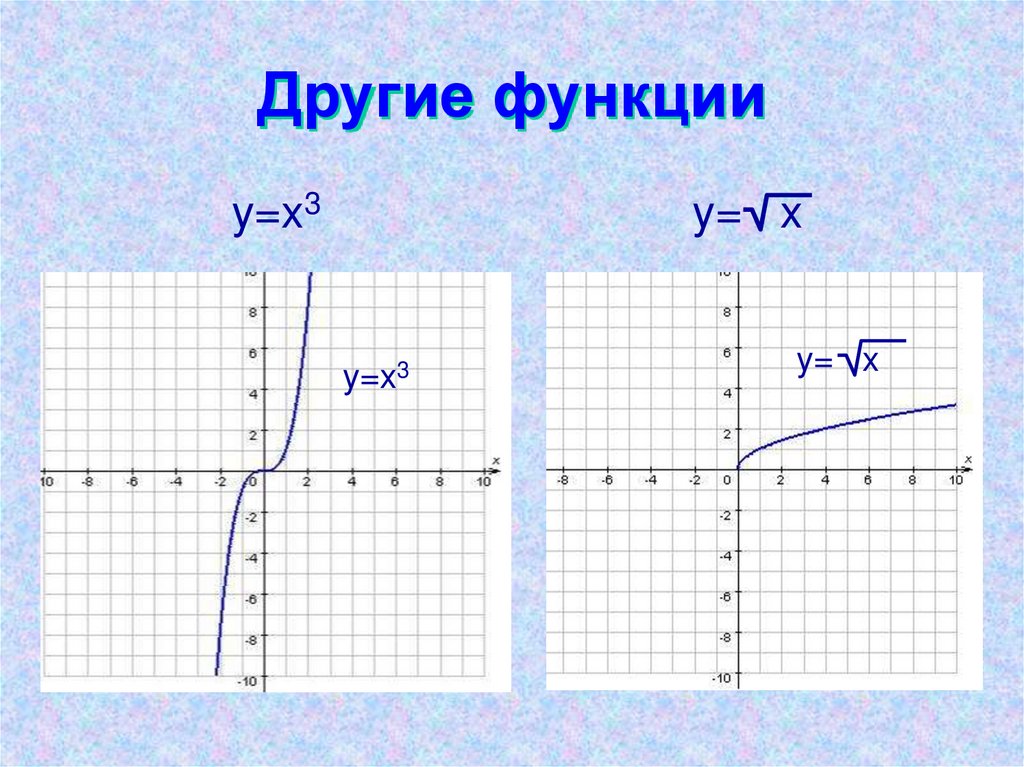
8. Другие функции

y=x3
y= x
y=x3
y= x

9. Основные приемы преобразований графиков:

• параллельный перенос графика y=f(x)
вдоль оси абсцисс;
• параллельный перенос графика y=f(x)
вдоль оси ординат;
• симметрия графика y=f(x) относительно
оси абсцисс;
• симметрия графика y=f(x) относительно
оси ординат;
• растяжение (сжатие) графика y=f(x)
вдоль оси ординат

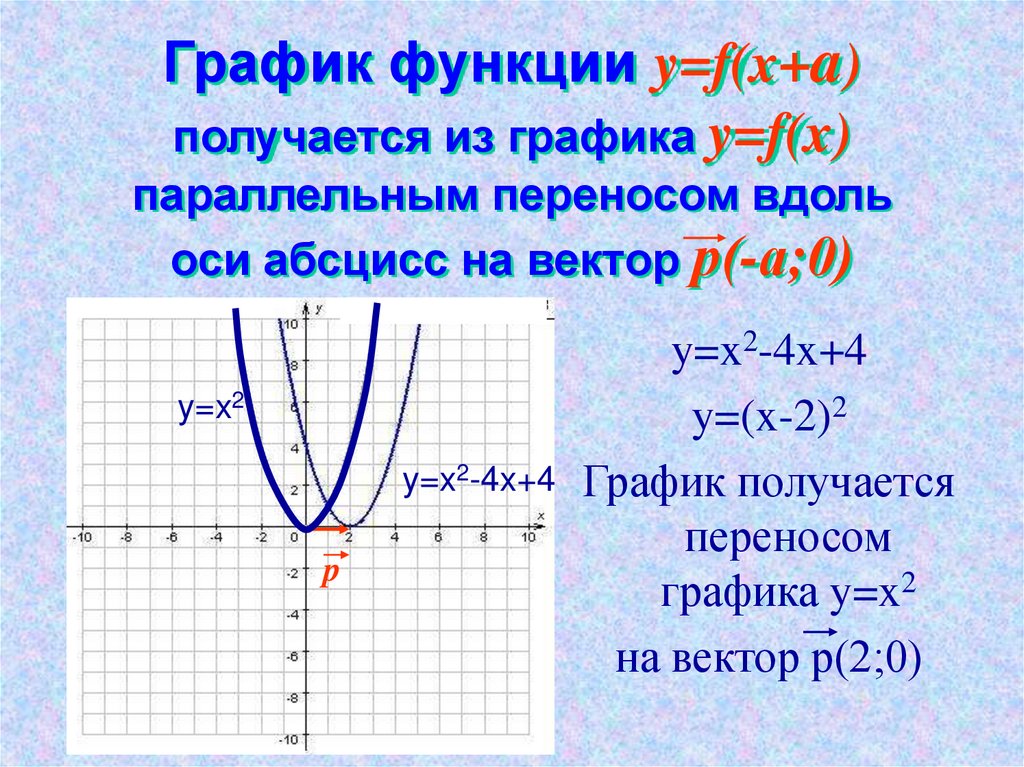
10. График функции y=f(x+a) получается из графика y=f(x) параллельным переносом вдоль оси абсцисс на вектор р(-а;0)

y=x2
y=x2-4x+4
p
y=x2-4x+4
y=(x-2)2
График получается
переносом
графика y=x2
на вектор р(2;0)

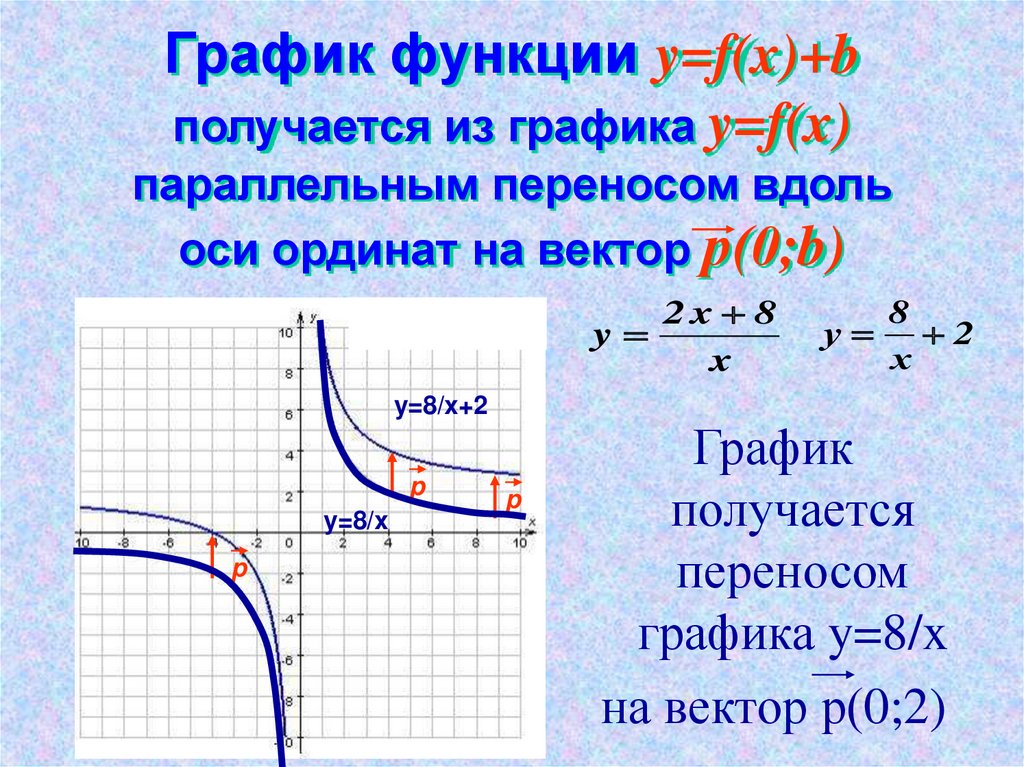
11. График функции y=f(x)+b получается из графика y=f(x) параллельным переносом вдоль оси ординат на вектор р(0;b)

2x 8
y
x
y=8/x+2
p
y=8/x
p
p
8
у 2
х
График
получается
переносом
графика y=8/x
на вектор р(0;2)

12. График функции y=-f(x) получается из графика y=f(x) симметрией относительно оси абсцисс

y=x2-6x+8
y=-x2+6x-8
y= -x2+6x-8
y= -(x2-6x+8)
График получается
симметрией графика
у= x2-6x+8
относительно
оси абсцисс

13. График функции y=f(-x) получается из графика y=f(x) симметрией относительно оси ординат

y= -x
y= x
y= -х
График получается
симметрией
графика
у= х
относительно
оси ординат

14. График функции y=kf(x) получается из графика y=f(x)

k>1
растяжением вдоль
оси ординат в k раз
0<k<1
сжатием вдоль оси
ординат в 1/ k раз
y=4x2
y=x2
y=x2
y=½x2