Похожие презентации:
Газодинамический расчёт ступени паровой турбины
1. Газодинамический расчёт ступени паровой турбины
Национальный исследовательский университет«Московский энергетический институт»
Кафедра Паровых и газовых турбин им. А.В. Щегляева
Газодинамический расчёт ступени паровой
турбины
к.т.н., доцент Чусов С.И.
Курс «Энергетические машины и
теплообменные установки»
для групп С-02
НИУ «МЭИ», Кафедра Паровых и газовых турбин им. А.В. Щегляева
2.
Содержание1. Преобразование энергии в турбинной ступени.
2. Геометрические характеристики осевой ступени.
3. Усилия на рабочих лопатках.
4. Основные потери в лопаточных решётках, относительный
лопаточный КПД.
3.
1. Преобразование энергиив турбинной ступени
4.
Принцип работы турбиныРабота турбины основана на возникновении
подъёмной
силы
при
обтекании
потоком
крыловидного профиля.
Для получения подъёмной силы необходимо иметь
высокоскоростной поток рабочего тела (пара или
газа) и крыловидные профили, при обтекании
которых и будет возникать подъёмная сила. Если
эти профили, называемые рабочими лопатками,
закрепить на валу турбины на определённом
расстоянии друг от друга, образуя тем самым
рабочую
решётку,
то
подъёмная
сила,
прикладываемая у центру масс каждой рабочей
лопатки, будет передаваться на вал и вызывать его
вращение.
Рис. 1. Фрагмент кольцевой лопаточной
решётки
5.
Физические свойства рабочего тела в турбомашинахРабочим телом в турбомашинах является пар или газ. Однако, с точки
зрения гидрогазодинамики, их можно рассматривать как частные случаи
жидкости.
В отличие от твёрдых тел, в которых молекулярные силы сцепления весьма
велики, жидкости, и в особенности газы, обладают относительно слабыми
межмолекулярными связями. Эта особенность их физической природы
проявляется в лёгкой подвижности, т.е. текучести или деформируемости:
движение жидкостей и газов под действием внешних и внутренних сил
сопровождается изменением формы, а в общем случае – и объёма
выделенной её части.
В гидрогазодинамике обычно абстрагируются от молекулярной структуры
исследуемых потоков и рассматривают условную модель среды,
обладающей
непрерывным
распределением
всех
характеристик
(параметров). Гипотеза непрерывности (сплошности) объединяет жидкости
и газы в единую категорию текучих, легко деформируемых сред.
6.
Физические свойства рабочего тела в турбомашинахВместе с тем между жидкостями и газами существует принципиальное
различие. В жидкостях силы межмолекулярного сцепления более
значительны по сравнению с газами, так как расстояния между молекулами
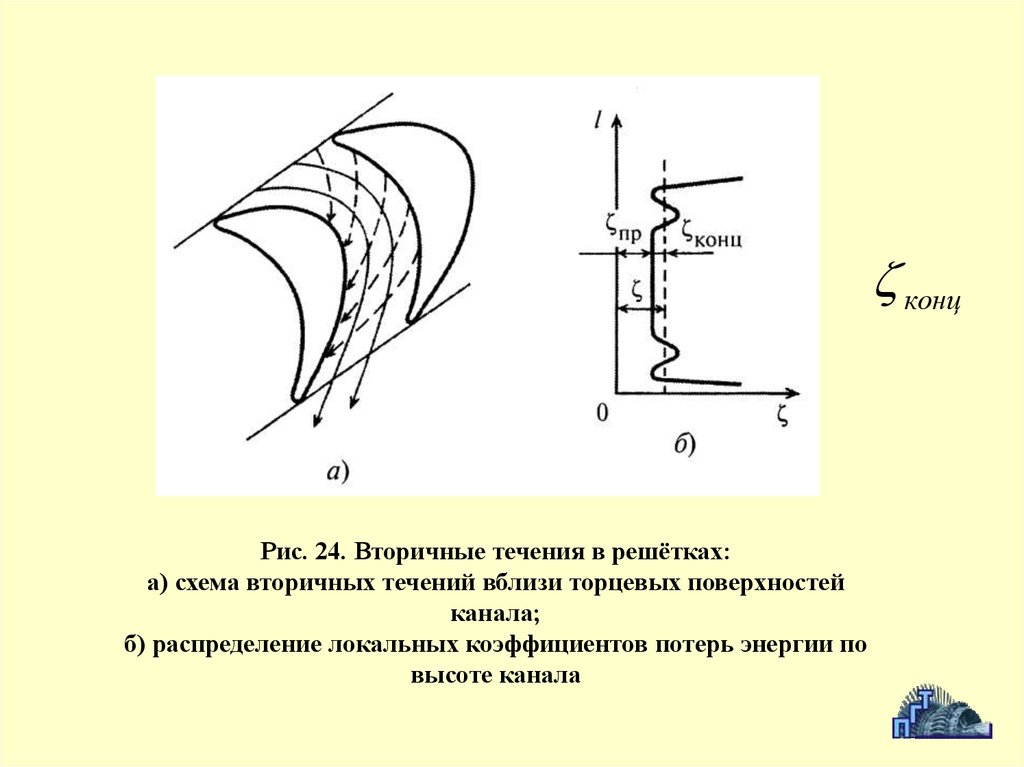
малы. По этой причине жидкости можно считать слабосжимаемыми
средами или, упрощенно, несжимаемыми.
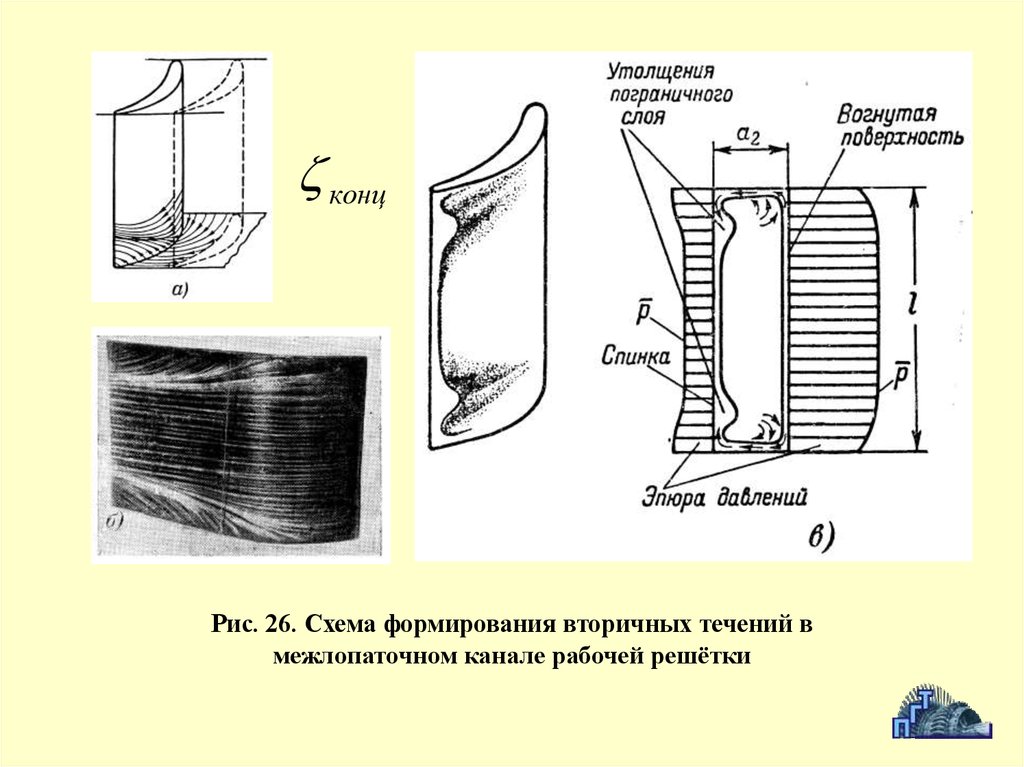
В газах расстояния между молекулами значительно больше, чем в
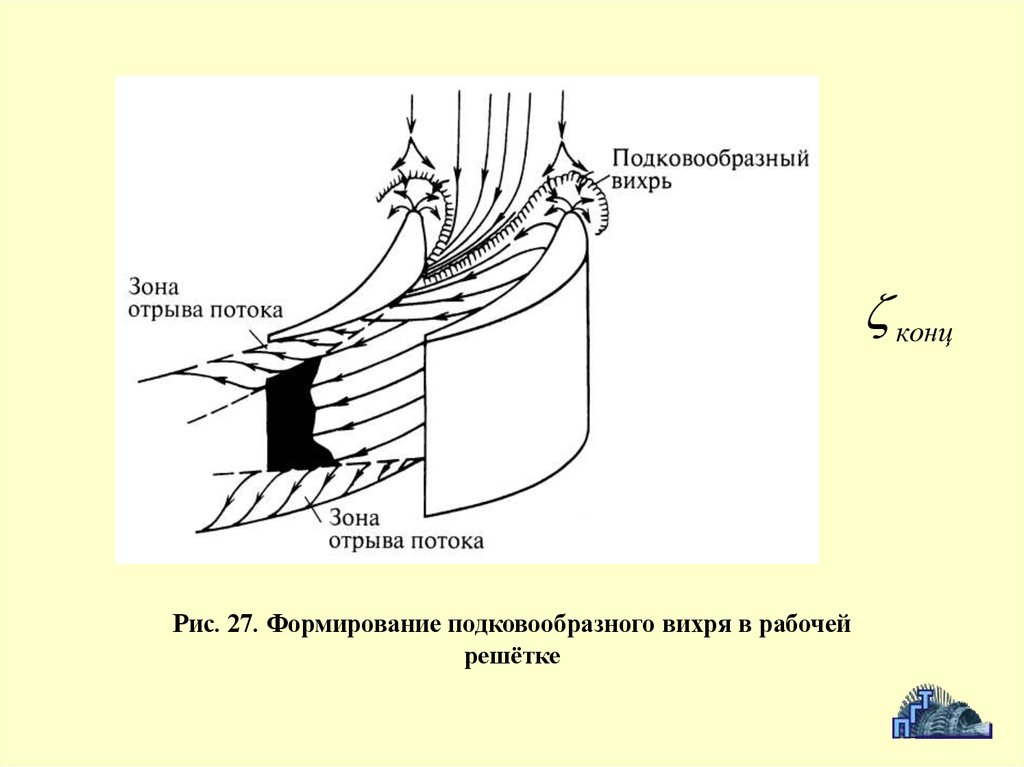
жидкостях, и силы молекулярного взаимодействия поэтому относительно
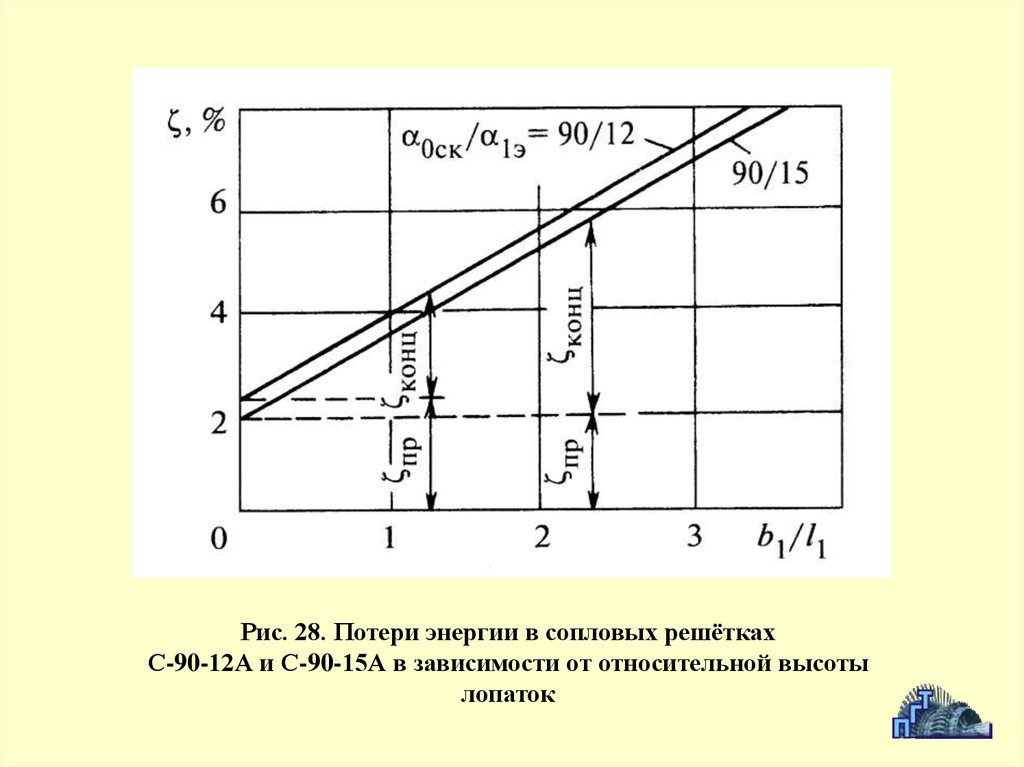
малы. Этой особенностью молекулярной структуры газов объясняется их
существенно большая по сравнению с жидкостью сжимаемость. При этом
жидкость принимает форму сосуда, в который она заключена, но образует
поверхность свободного уровня. На такой поверхности особенно интенсивно
сказывается воздействие молекулярных сил сцепления, что приводит к
появлению свойств капиллярности, смачиваемости твёрдых поверхностей и
к возникновению капель и менисков. Хорошо известно, что газы целиком
заполняют сосуд, в который они помещены, и не образуют поверхности
свободного уровня.
7.
Физические свойства рабочего тела в турбомашинахЭффекты сжимаемости интенсивно проявляются при движении газов в
каналах с большими скоростями и при обтекании тел различной формы
потоком с большой скоростью. При небольших скоростях и в отсутствие
теплообмена сжимаемость газов сказывается слабо. Вместе с тем
сжимаемость капельных жидкостей также обнаруживается при больших
давлениях. Отсюда следует, что сжимаемость свойственна всем жидкостям и
газам, однако её количественное проявление будет различным в зависимости
от физических свойств среды. Это послужило основанием объединить
сплошные среды, обладающие общим свойством сплошности и лёгкой
подвижности, под общим названием жидкости, выделяя по мере
необходимости практически несжимаемые (капельные) и сжимаемые
(газообразные) жидкости.
8.
Физические свойства рабочего тела в турбомашинахВсе жидкости обладают внутренним трением, обусловленным вязкими
свойствами среды. Влияние вязкости на характер течения жидкости
неоднозначно. В некоторых задачах вязкость играет решающую роль и
определяет движение среды. В других случаях её влияние сказывается
слабо, и представление о характере течения можно получить без учёта
вязких сил. Пренебрежение вязкими силами существенно облегчает
аналитическое исследование, и вместо реальной жидкости оказывается
целесообразным рассматривать модель идеальной жидкости.
Идеальная жидкость – это абстрактная жидкость, лишённая внутренних
сил трения. Указанную модель следует рассматривать как первое, но важное
приближение к реальной модели течения. При изучении вязких свойств
обнаруживается также различие между капельной и сжимаемой жидкостью,
обусловленное молекулярной структурой: вязкость несжимаемой жидкости
с ростом температуры уменьшается, а вязкость газов растёт.
9.
Физические основы одномерной теории турбомашинРеальные процессы протекания рабочего тела (пара, газа) в турбомашинах
трёхмерны (по осям x, y, z), однако трёхмерный расчёт сопряжён со
значительными трудностями. В большинстве случаев оказывается
оправданным считать движение рабочего тела одномерным, т.е.
предполагать, что изменение параметров рабочего тела происходит в одном
направлении (условно, по оси x).
При расчёте турбомашин непрерывное течение рабочего тела можно
рассматривать как равновесный процесс. Это означает, что движущееся
рабочее тело находится в термодинамическом равновесии и имеет вполне
определённые значения параметров (температуры T или t, давления p,
энтальпии h, энтропии s и т.д.), непрерывно изменяющиеся с течением
времени (в конкретной точке) и при переходе от одной точки к другой.
Кроме того, движение рабочего тела считают установившимся или
стационарным. Это означает, что в каждой точке потока рабочего тела все
параметры имеют определённые, не изменяющиеся во времени значения.
Таким образом, мы будем рассматривать одномерное установившееся
течение рабочего тела.
10.
Физические основы одномерной теории турбомашинДля расчёта течения жидкости используют 4 закона, выражающихся
следующими уравнениями:
- уравнение состояния;
- уравнение неразрывности (сохранения массы);
- уравнение сохранения количества движения (уравнение импульса);
- уравнение сохранения энергии (1-й закон термодинамики).
11.
Уравнение состоянияДля идеального газа уравнение состояния имеет вид:
p R T
или
p
R T
и связывает основные параметры газа: давление [Па], температуру [K] и
удельный объём [м3/кг] или плотность [кг/м3].
Здесь R [Дж/кг·К] – газовая постоянная, представляющая собой работу 1 кг
газа при его нагреве на 1 К.
Принимается R = 287 [Дж/кг·К] (воздух); R = 461 [Дж/кг·К] (пар)
Для перегретого пара уравнение состояния в указанном виде неточно, т.к. R
зависит от давления и температуры. Значительно точнее соблюдается
зависимость:
h
1
p const
Иногда пар, свойства которого удовлетворяют этому уравнению,
называют «идеальным».
12.
Уравнение состояния и изоэнтропыЗдесь κ – показатель изоэнтропы, который зависит от температуры и
выражается как
сp
c
Принимается в среднем κ = 1,4 для воздуха и κ = 1,3 для перегретого
пара (точнее, от 1,26 до 1,33), а для сухого насыщенного пара κ =
1,26 ÷ 1,33.
Если предположить, что расширение газа происходит без потерь и
без теплообмена с внешней средой, то этот процесс называется
изоэнтропийным и газ подчиняется уравнению изоэнтропы:
p t const
где индекс t означает, что процесс идет по изоэнтропе.
13.
Уравнение неразрывностиМассовым расходом газа G [кг/с] называют массу газа m [кг],
которая проходит через поперечное сечение канала в единицу
времени τ [с], т.е.:
m
G
Рис. 2. К выводу уравнения
неразрывности
Массовый расход газа G через любое поперечное сечение канала
сохраняется постоянным, т.е.:
G
F c
const
или
G с F const
Здесь – удельный объем [м3/кг], а – плотность [кг/м3].
14.
Уравнение сохранения количества движения (импульса)Уравнение изменения количества движения (уравнение импульса) в
одномерном потоке (для установившегося течения) имеет вид:
dр R dx с dc
(вывод данного уравнения см. на стр. 42 «Красной книжки»-2008)
где υ – удельный объём, dp – приращение давления, R – сила
сопротивления внешней среды, отнесённая к 1 кг массы
протекающего газа, dx – длина трубки тока, с – скорость потока газа,
dc – приращение скорости.
Интегрируя это выражение на участке конечного пути перемещения
газа, перейдем от уравнения количества движения к частному
случаю уравнения сохранения энергии:
р
0
1
с12 с02
dp Rdx
2
р1
x0
x
15.
Уравнение сохранения количества движения (импульса)Здесь левая часть представляет собой приращение кинетической
энергии потока, которая равняется разности работы расширения газа
при истечении (первый интеграл в правой части) и работы сил
трения (второй интеграл в правой части).
Для того, чтобы найти приращение кинетической энергии, надо
проинтегрировать правую часть уравнения, а для этого нужно знать
закон изменения состояния υ = f (p) и закон изменения сил
сопротивления R = f (x). Особенно просто эта задача решается в
случае изоэнтропийного течения, т.е. течения без потерь и без
теплообмена с окружающей средой. Тогда R = 0, а закон изменения
состояния выражается уравнением изоэнтропы:
р0 0 р t const
16.
Уравнение сохранения количества движения (импульса)Найдя из уравнения изоэнтропы:
1
p0
t 0
p
и подставляя под интеграл, получаем:
р0
1
p0
с12t с02
0 dp
2
p
р1
Решая этот интеграл, получаем окончательно:
17.
Уравнение сохранения количества движения (импульса)с12t с02
p0 0 р1 1t
2
1
Данное выражение было получено для трубки тока, имеющей в
основаниях элементарные площади f0 и f1. Однако этот вывод
можно распространить и на весь канал, только в этом случае под
скоростями, давлениями и удельными объёмами следует
подразумевать их осреднённые по сечению значения.
18.
Уравнение сохранения энергииПреобразование внутренней энергии газа в работу в турбине
происходит в соответствии с первым законом термодинамики,
конкретная запись которого для быстро движущегося газа имеет
специфическую форму.
Рассмотрим протекание газа по каналу переменного сечения.
Осреднённые параметры газа на входе:
p0 , 0 , Т 0 , с0
На выходе:
p1 , 1 , Т1 , с1
Допустим, что на участке канала 0-0 – 1-1 подводится теплота q и
отводится работа l (см. рис. 3).
Рис. 3. К выводу уравнения
энергии
19.
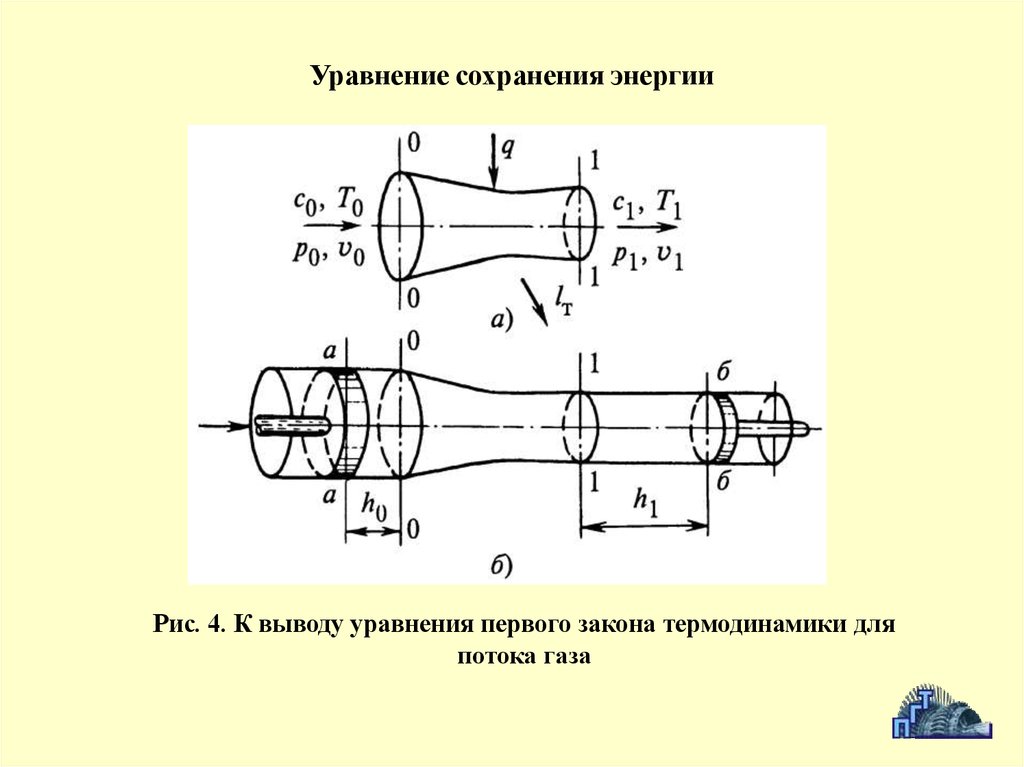
Уравнение сохранения энергииРис. 4. К выводу уравнения первого закона термодинамики для
потока газа
20.
Уравнение сохранения энергииВ соответствии с первым законом термодинамики подводимая к
системе теплота расходуется на повышение внутренней энергии и
совершение работы, т.е.:
q u l
где первый член в правой части – изменение внутренней энергии –
выражается как:
u u1 u0
а второй член, l – работа, имеет несколько составляющих.
Если канал движется, то совершается техническая работа lT. В
частности, это относится к каналам, расположенным на роторе
турбины, т.е. каналам между рабочими лопатками.
Далее, поскольку скорости газа в сечениях 0-0 и 1-1 разные,
произойдет изменение кинетической энергии на величину:
с12 с02
lк
2 2
21.
Уравнение сохранения энергииТретья составляющая – работа проталкивания, т.е.:
lп р1 1 р0 0
Тогда суммарная работа записывается как:
l lт lк lп
Вернёмся теперь к записи первого закона термодинамики и
подставим в него все найденные члены:
с12 с02
q u l u1 u0 lт lк lп u1 u0 lт р1 1 р0 0
2 2
Учтём теперь, что, согласно уравнению Клапейрона-Менделеева,
энтальпия h является суммой внутренней энергии u и энергии
проталкивания p·υ, т.е.:
h u р
22.
Уравнение сохранения энергииТогда:
с12 с02
q u1 р1 1 u0 р0 0 lт
2 2
Или:
с12 с02
q h1 h0 lт
2 2
Таким образом, теплота, подводимая к потоку газа, расходуется на
изменение его энтальпии, изменение кинетической энергии и
совершение технической работы.
Это выражение называется уравнением сохранения энергии для
установившегося потока. Оно справедливо независимо от того,
сопровождается ли течение газа потерями или нет.
23.
Уравнение сохранения энергииПолученные уравнения позволяют решать ряд практических задач
для расчёта течения в каналах. Например, предположим, что газ
движется в неподвижном канале без теплообмена с окружающей
средой. Тогда:
lт 0
и
q 0
Такое течение соответствует изоэнтропийному течению в
неподвижных каналах – соплах. Тогда из уравнения энергии, приняв
на входе в сопло параметры с индексом 0, а на выходе – 1,
получается:
с12 с02
0 h1 h0 0
2 2
Или:
с12 с02
h0 h1
2 2
24.
Уравнение сохранения энергииУчитывая выражение для «идеального пара»
h
1
p
можно записать:
с12 с02
p0 0
p1 1
1
1
2 2
Преобразуя его, получаем окончательно:
с12 с02
p0 0 p1 1
2 2 1
25.
Уравнение сохранения энергииТаким образом, для частного случая уравнения энергии мы
получили почти такую же запись, как итоговое выражение для
уравнения сохранения количества движения. Различие будет в том,
что у скорости с1 и у удельного объема υ1 там был ещё индекс t,
обозначавший изоэнтропийное течение, а в последней записи из
уравнения энергии индекса t нет. Это означает, что в последнем
выражении для получения реальной скорости с1 в конце процесса
расширения газа нам необязательно знать закон изменения
удельного объёма от плотности υ = f (p) и закон изменения сил
сопротивления от линейной координаты R = f (x), а достаточно
знать только значения энтальпий в начале и в конце процесса.
26.
Вывод зависимости между законом изменения площадиканала и скоростью потока
G c F
ln G ln ln c ln F
dG d dc dF
G
c
F
Т.к.
G const
d
, то
dG 0
dc dF
0
c
F
и
dG
0
G
(*)
27.
Из уравнения импульса следует:с dc
dр
Домножим второй член на
dр d
с dc
0
d
0
d
d
dр d
с dc
0
d
По определению, скорость звука выражается как:
dр
а
d
28.
Тогда:с dc а
2
d
По определению, число Маха
0
с
М
а
Разделим последнее уравнение на
с
с dc а 2 d
2
0
2
с
с
dc
1 d
2
0
с М
d
dc
М
с
2
2
29.
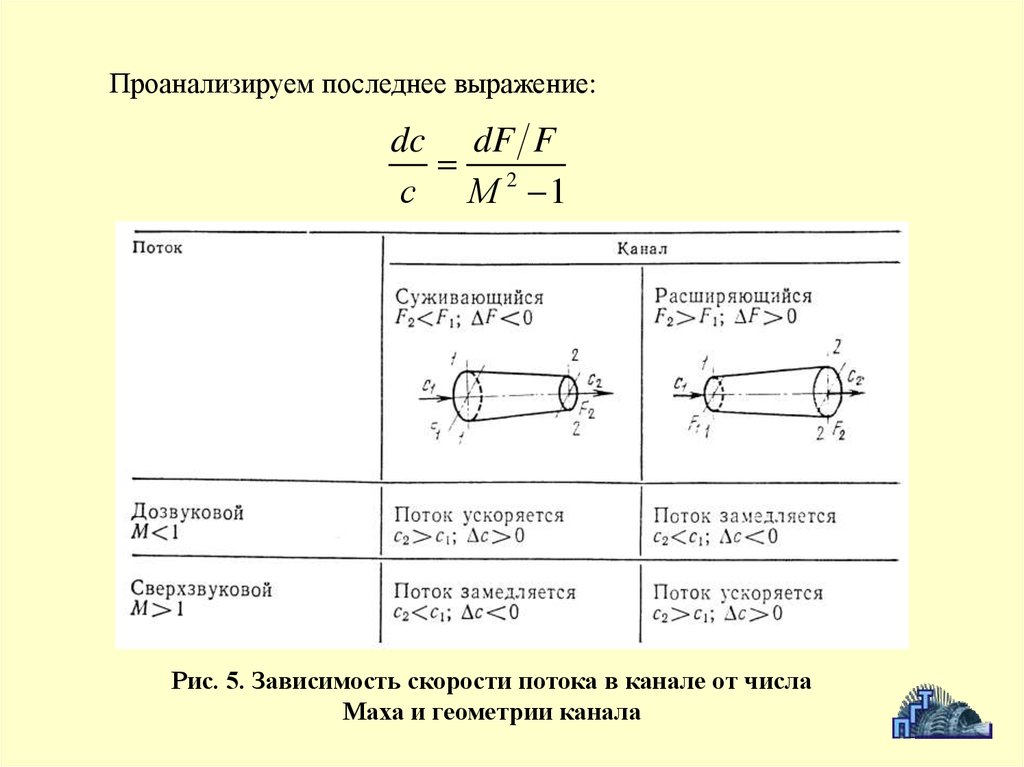
Проанализируем последнее выражение:dc dF F
2
с М 1
Рис. 5. Зависимость скорости потока в канале от числа
Маха и геометрии канала
30.
Одномерные течения в каналах разделяются на:конфузорные и диффузорные
Конфузорными называют такие течения в каналах, когда
скорость рабочего тела увеличивается в направлении движения
потока.
Диффузорными называют такие течения в каналах, когда
скорость рабочего тела уменьшается в направлении движения
потока.
При дозвуковом течении суживающийся канал является
конфузорным, а расширяющийся – диффузорным. При
сверхзвуковом течении, соответственно – наоборот.
Таким образом, при дозвуковом течении для увеличения
скорости потока необходимо применять суживающиеся
каналы.
31.
Подставим последнее выражение в уравнение (*):dc dc dF
М
0
с
c
F
2
dc
dF
2
1 М
0
с
F
dc dF F
с
1 М 2
dc dF F
2
с М 1
32.
Кроме того, суживающиеся каналы должны подавать потокрабочего тела к рабочим лопаткам под определённым углом,
т.е. эти каналы должны быть изогнутыми.
Рис. 6. Изогнутый сопловой
канал
Такие каналы можно получить, располагая так называемые
сопловые лопатки на определённом расстоянии друг от друга,
образуя сопловую решётку. Именно в суживающихся
изогнутых межлопаточных каналах сопловой решётки
потенциальная энергия пара преобразуется в кинетическую
энергию потока пара. Совокупность сопловых и рабочих
решёток называется ступенью турбомашины.
33.
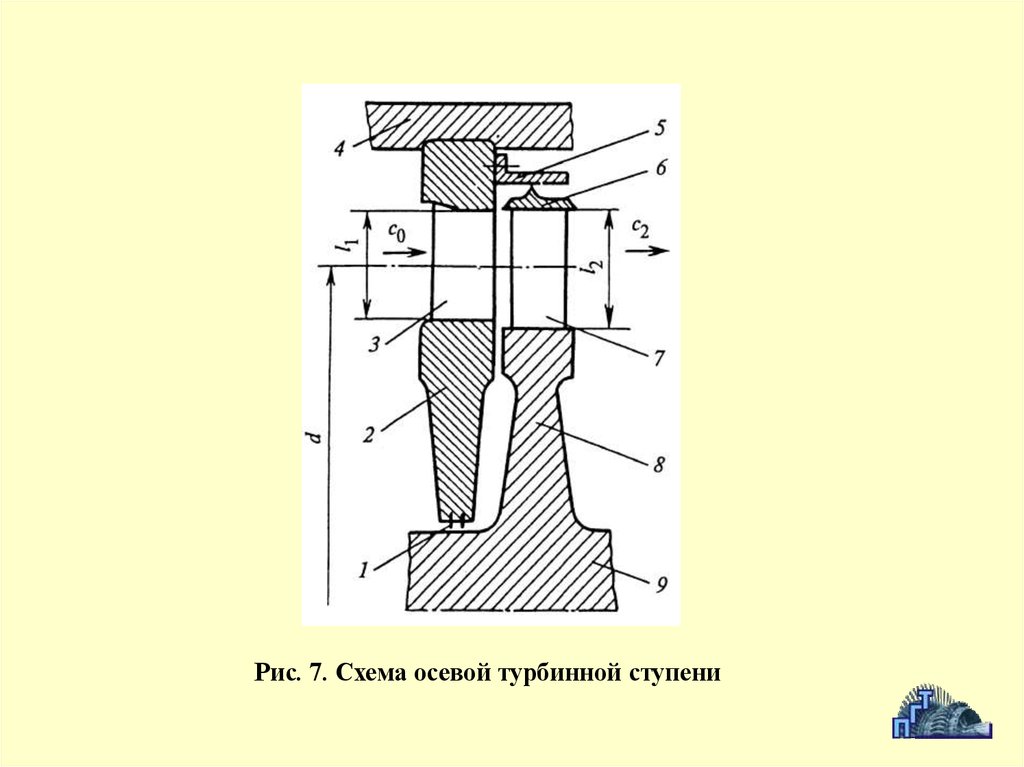
Рис. 7. Схема осевой турбинной ступени34.
2. Геометрические характеристикиосевой ступени турбины
35.
Рис. 8. Турбинные решёткиа) сектор кольцевой лопаточной решётки;
б) пакет плоской решётки профилей
36.
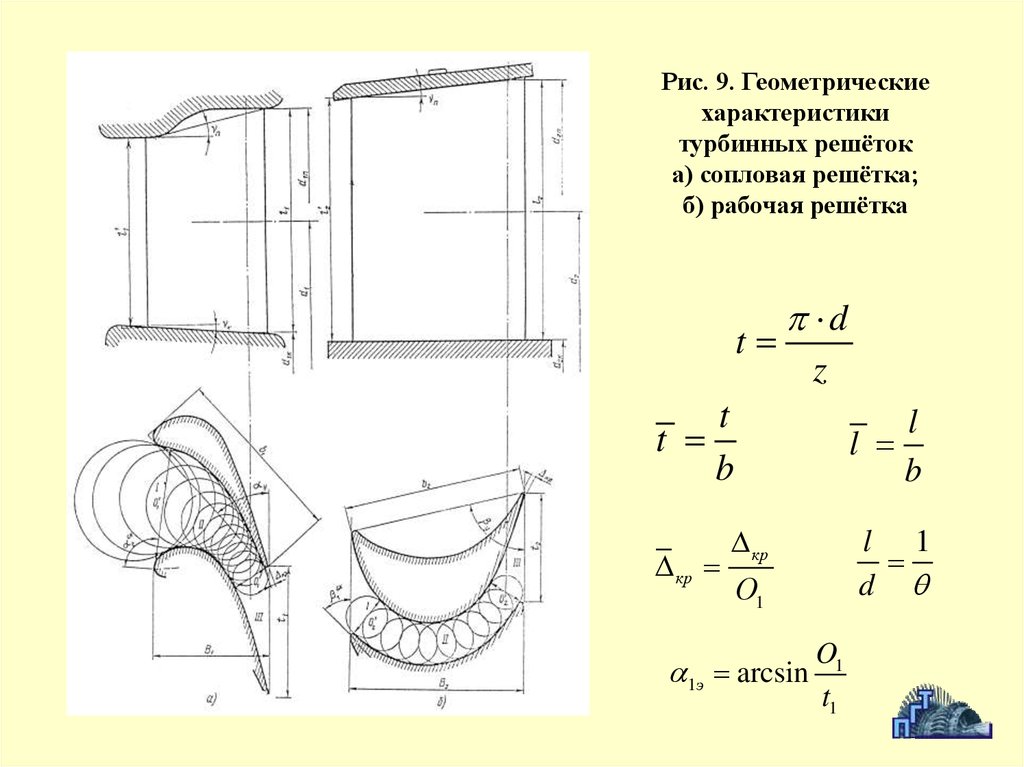
Рис. 9. Геометрическиехарактеристики
турбинных решёток
а) сопловая решётка;
б) рабочая решётка
t
d
z
t
t
b
кр
l
кр
l 1
d
О1
1э arcsin
l
b
O1
t1
37.
Рис. 10. Расширение пара в косом срезе сопловой решётки присверхзвуковых скоростях потока на выходе из неё
38.
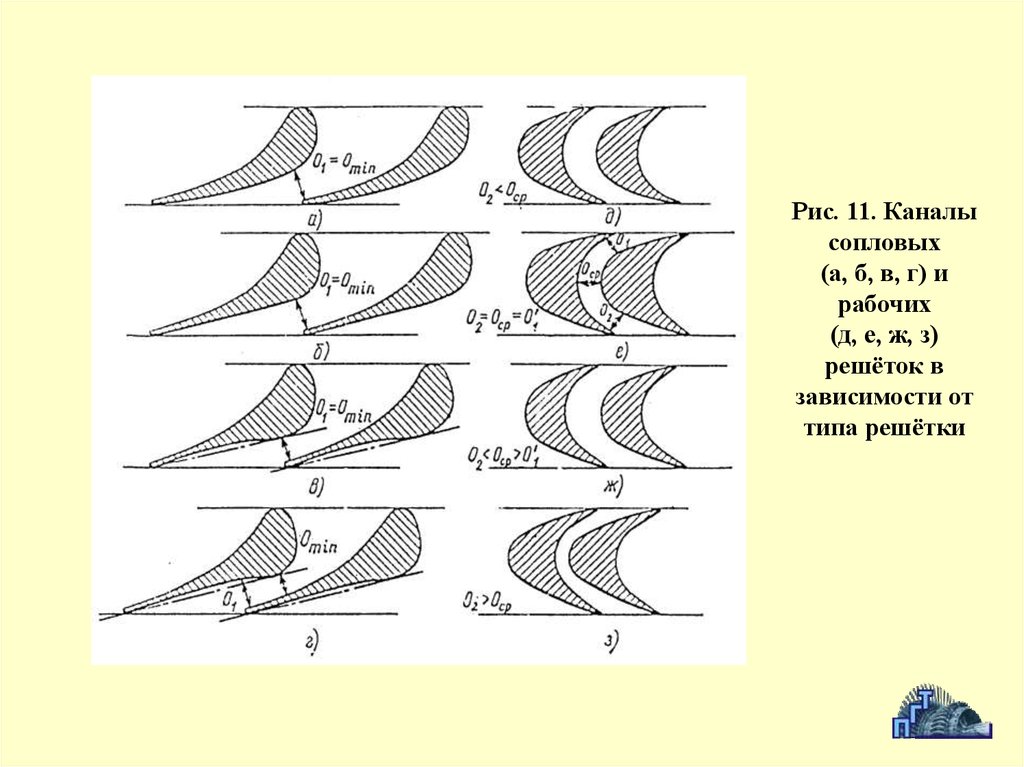
Рис. 11. Каналысопловых
(а, б, в, г) и
рабочих
(д, е, ж, з)
решёток в
зависимости от
типа решётки
39.
Рис. 12. Классификация решёток по типу40.
Рис. 13. Процесс в соплах (сопловых решётках)в h-s–диаграмме
41.
Уравнение энергии для точек0и
1tзаписывается как:
2
c12t c0
h0 h1t
2 2
Отсюда получаем выражение для скорости в точке
c1t 2 (h0 h1t ) c0 2
Из уравнения энергии для точек
0и
c1 2 (h0 h1 ) c0 2
:1
: 1t
42.
Из уравнения энергии для точек1и
1tимеем:
2
c1
с c
c c c
Н с h1 h1t
1 1
2
2 c 2 c1t
c1
Отношение
называется коэффициент скорости
c1t
c1
(обычно
сопловой решётки и обозначается
0,93-0,98)
c1t
2
c
Тогда:
Н с 1t 1 2
2
2
1t
2
1
2
1t
2
1
2
1t
2
1t
Величина, характеризующая потерю энергии из-за действия
сил трения, называется коэффициент потери энергии в
сопловой решётке и обозначается:
с 1 2
43.
Из выраженияc1t 2 (h0 h1t ) c0 2
и h-s–
диаграммы для сопловой решётки (рис. 13) следует:
c1t 2 (h0 h1t ) c0 2
С учётом того, что скорость
с0 0
,а
h0 h1t Н 0:с
c1t 2 (h0 h1t ) c0 2 2 H 0c
Тогда потери в сопловой решётке можно записать как:
2
c
c
2
0
Н с 1 h0 h1t 1 2 H 0c 1 2
2
2
2
1t
Н с H 0c с
44.
Важной характеристикой решётки является коэффициент расходаμ. Если бы течение в решётке было изоэнтропным, то через неё
протекал бы теоретический расход
Glt = сlt/(F·υlt),
где υlt – удельный объём пара в конце изоэнтропного расширения.
В реальных условиях из-за образования на стенках канала
пограничного слоя расход G оказывается меньше теоретического;
величина
μ = G/Glt
называется коэффициентом расхода. Для турбинных решёток,
работающих на перегретом паре, μ = 0,93÷0,98, а на влажном μ =
0,94÷1,04.
45.
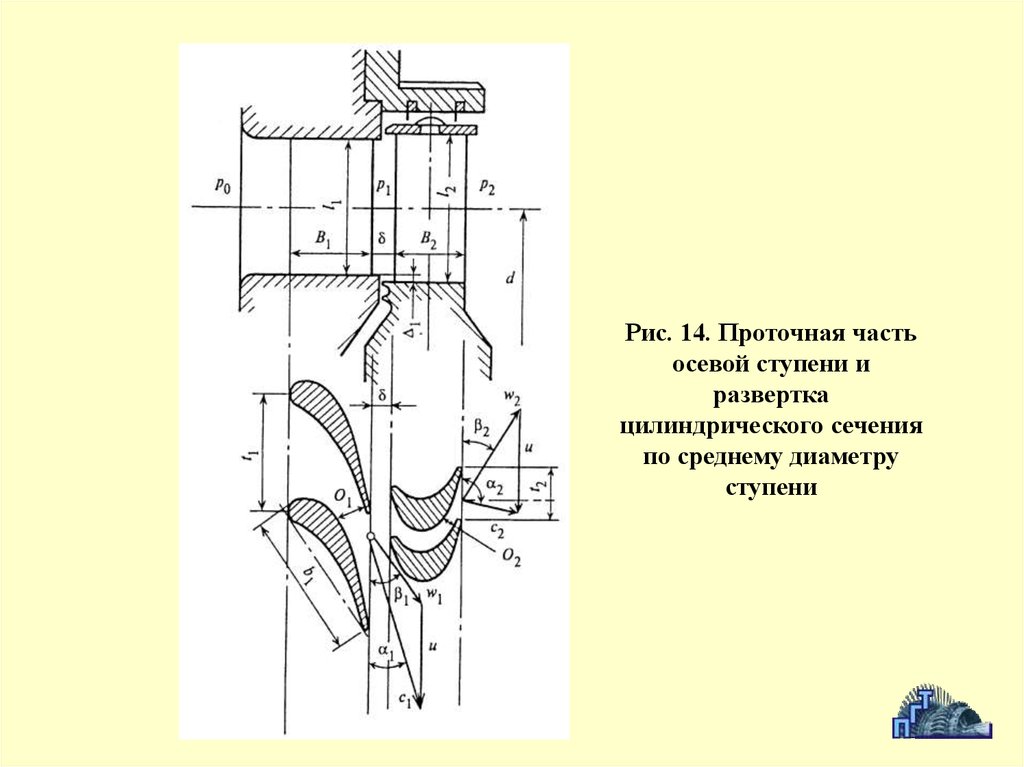
Рис. 14. Проточная частьосевой ступени и
развертка
цилиндрического сечения
по среднему диаметру
ступени
46.
Рис. 15. Схема процесса в ступени в h-s-диаграмме47.
Рис. 16. Треугольники скоростей для потока втурбинной ступени
48.
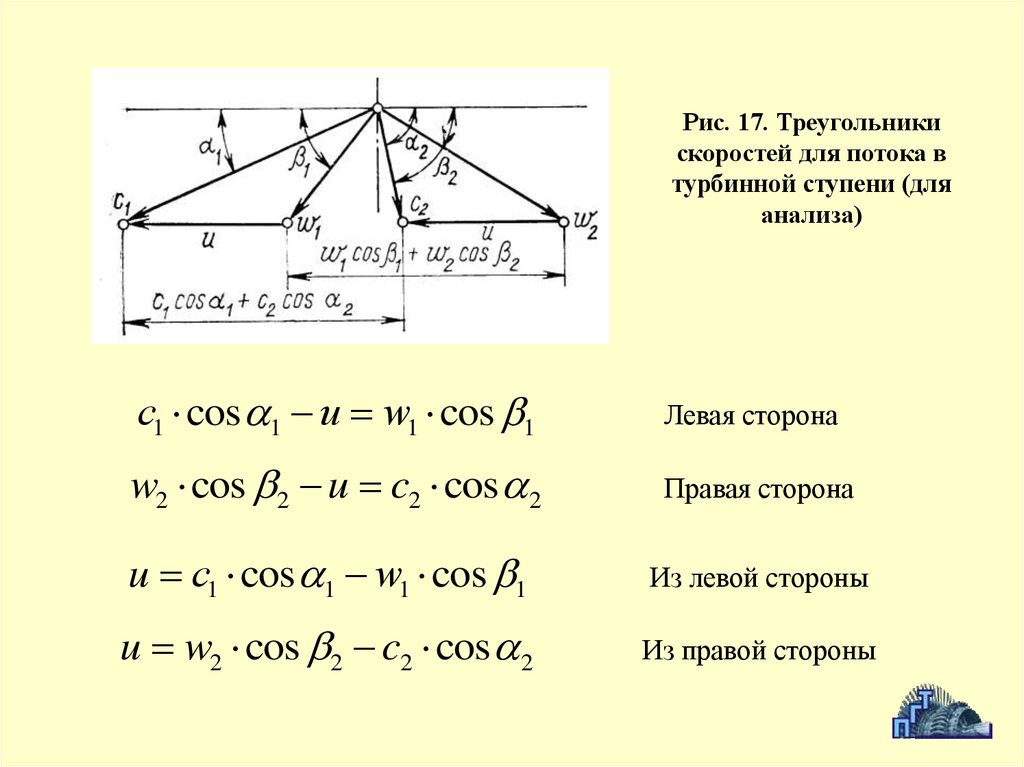
Рис. 17. Треугольникискоростей для потока в
турбинной ступени (для
анализа)
с1 cos 1 u w1 cos 1
Левая сторона
w2 cos 2 u c2 cos 2
Правая сторона
u с1 cos 1 w1 cos 1
Из левой стороны
u w2 cos 2 c2 cos 2
Из правой стороны
49.
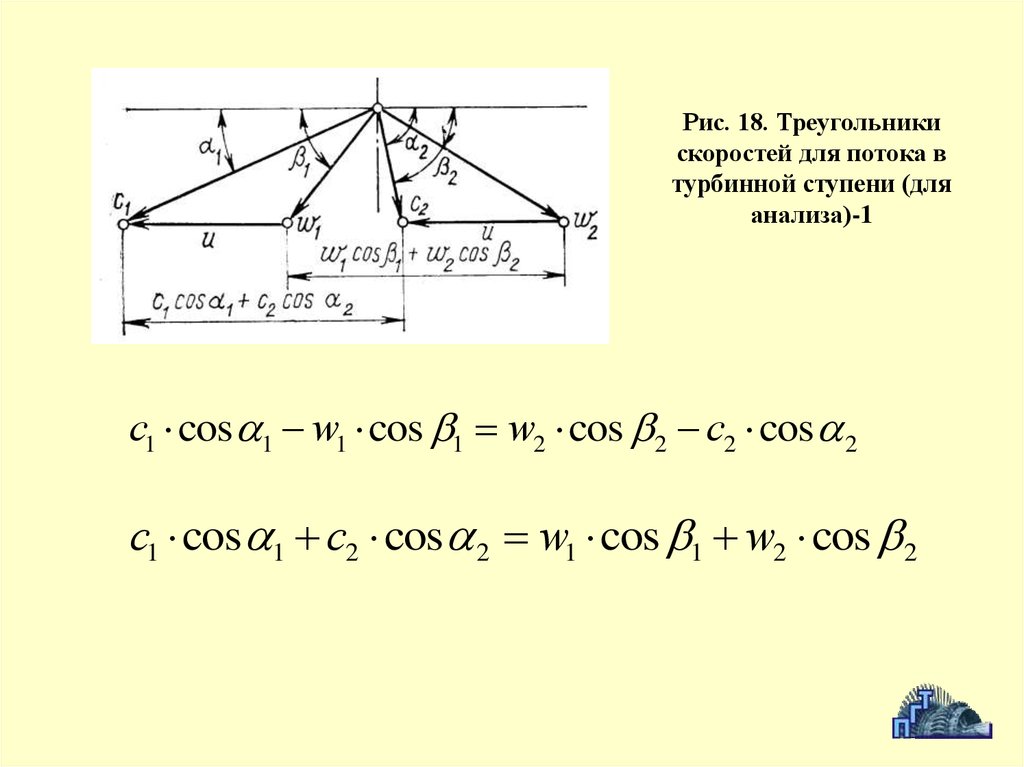
Рис. 18. Треугольникискоростей для потока в
турбинной ступени (для
анализа)-1
с1 cos 1 w1 cos 1 w2 cos 2 c2 cos 2
с1 cos 1 c2 cos 2 w1 cos 1 w2 cos 2
50.
Рис. 19. Процесс в h-s–диаграмме для сопловой (а) и рабочей (б)решёток
51.
Соотношение между скоростями и углами потока в турбиннойступени в большой степени зависит от степени реактивности
ступени ρ. Под степенью реактивности понимается отношение
располагаемого теплоперепада рабочих лопаток к сумме
располагаемых теплоперепадов сопловых и рабочих лопаток,
приближенно равной теплоперепаду ступени от параметров
полного торможения:
Н0 р
Н 0с Н 0 р
Н0 р
Н0
52.
Проведём расчёт для осевой турбинной ступени, предполагаяизвестными
,
и начальную
пара . Кроме того,
t0
р0 скорость
предполагаются
заданными или принимаемыми по ходу расчёта
с
0
,
,
,
,
и
1 d n
.
2
Кроме того, необходимо иметь либо значение располагаемого
теплоперепада на ступень
и
, либо давления
Н0
и
р1 р2
2
с12t c12 c12t
c
Н с h1 h1t
1 2 1t с
2
2
2
c1 2 (h0 h1 ) c0 2 2 (h0 h1t ) c0 2
2 H 0 с c0 2 2 H 0 с
.
53.
c1 2 H 0 с 2 Н 0 Н 0 р2 Н 0 Н 0 2 1 Н 0
u d n
w c u 2 u c1 cos 1
2
1
2
1
2
w22t
w12
h1
h2t
2
2
w22t w12
h1 h2t
2
2
tg 1
sin 1
u
cos 1
c1
54.
w2t w12 2 h1 h2t w12 2 Н 0 рw2t w12 2 Н 0 р w12 2 Н 0
Отношение
w2
w2t
называется коэффициентом
скорости рабочей решётки и обозначается
(обычно 0,92-0,96)
w2 w2t w12 2 h1 h2t
w12 2 H 0 р w12 2 H 0
55.
w2tw
w
w
H р h2 h2t
2
2
2
2
2
w22t
w
1 2 2t р
2
2
2
2t
2
2
c w u 2 u w2 cos 2
2
2
2
2
2
2
2
2t
tg 2
sin 2
u
cos 2
w2
56.
3. Усилия на рабочих лопатках57.
Усилия на рабочих лопаткахРис. 20. К выводу уравнения изменения количества
движения для турбинной ступени
58.
К выводу уравнения импульса для турбинной ступени:F m a
c
a
t
с
F m
t
F t m с
R dt p1 p2 dt dm c2 c1
d l2
59.
К выводу уравнения импульса для турбинной ступениdm
R p1 p2
c2 c1
dt
dm
G
dt
R p1 p2 G c2 c1
60.
К выводу уравнения импульса для турбинной ступениВ проекции на ось u:
Ru G c2u c1u
Ru G c2 cos 2 c1 cos 1
Ru Ru
Ru G c1 cos 1 c2 cos 2
61.
К выводу уравнения импульса для турбинной ступениВ проекции на ось a:
Ra p1 p2 G c2a c1a
Ra G c2a c1a p1 p2
Ra G c2 sin 2 c1 sin 1 p2 p1
Ra Ra
Ra G c1 sin 1 c2 sin 2 p1 p2
62.
К выводу уравнения импульса для турбинной ступениRu G c1 cos 1 c2 cos 2
Ra G c1 sin 1 c2 sin 2 p1 p2
2 2
cos cos
sin sin
Ru G c1 cos 1 c2 cos 2
Ra G c1 sin 1 c2 sin 2 p1 p2
63.
К выводу уравнения импульса для турбинной ступениИз треугольников скоростей следует (см. рис. 18):
c1 cos 1 c2 cos 2 w1 cos 1 w2 cos 2
Поэтому:
Ru G c1 cos 1 c2 cos 2
G w1 cos 1 w2 cos 2
Ra G c1 sin 1 c2 sin 2 p1 p2
G w1 sin 1 w2 sin 2 p1 p2
64.
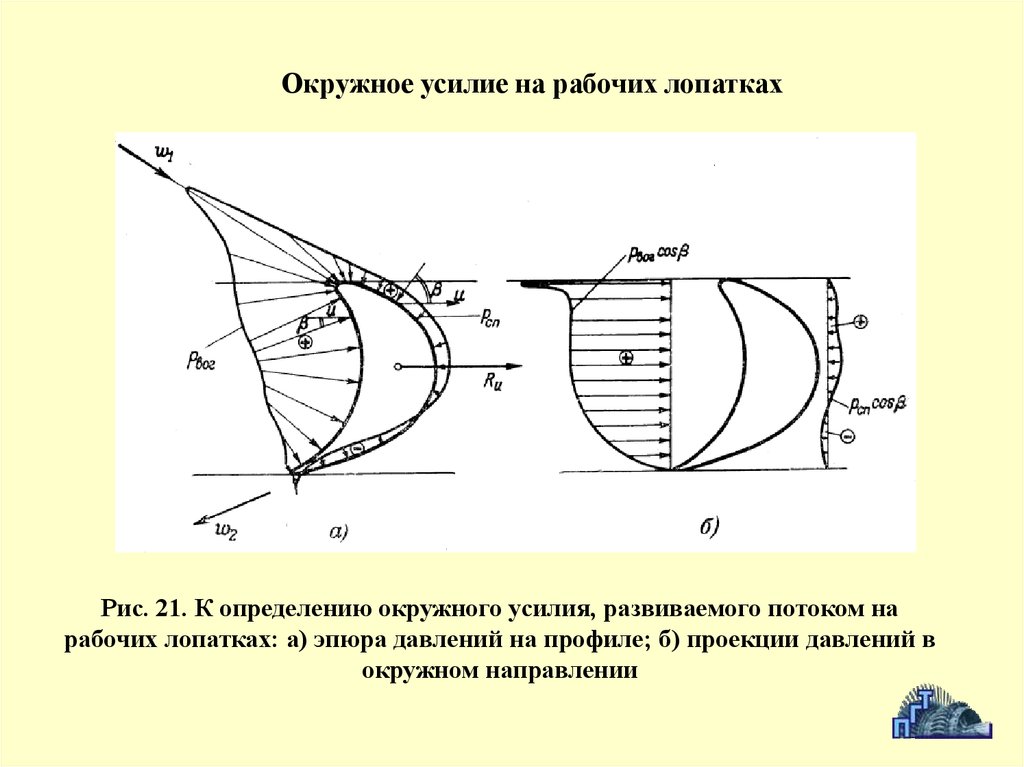
Окружное усилие на рабочих лопаткахРис. 21. К определению окружного усилия, развиваемого потоком на
рабочих лопатках: а) эпюра давлений на профиле; б) проекции давлений в
окружном направлении
65.
Мощность и удельная работа турбинной ступениNu Ru u
Nu Ru u G u c1 cos 1 c2 cos 2
G u w1 cos 1 w2 cos 2
Nu
Lu
G
Nu
Lu
u c1 cos 1 c2 cos 2
G
u w1 cos 1 w2 cos 2
66.
4. Основные потери в лопаточных решётках,относительный лопаточный КПД
67.
Рис. 22. Схема распределениятолщины пограничного слоя
по профилю лопатки для
безотрывного течения (а) и
для течения с отрывом
потока от спинки (б)
кр
68.
крРис. 23.
Распределение
скоростей,
относительных
давлений и углов
потока за решёткой
(сплошные линии при
y = 0,1 · t,
пунктирные – при
y = 1,8 · t)
69.
концРис. 24. Вторичные течения в решётках:
а) схема вторичных течений вблизи торцевых поверхностей
канала;
б) распределение локальных коэффициентов потерь энергии по
высоте канала
70.
концРис. 25. Схема формирования парных вихрей
71.
концРис. 26. Схема формирования вторичных течений в
межлопаточном канале рабочей решётки
72.
концРис. 27. Формирование подковообразного вихря в рабочей
решётке
73.
Рис. 28. Потери энергии в сопловых решёткахС-90-12А и С-90-15А в зависимости от относительной высоты
лопаток
74.
Потери в ступени турбиныпр конц
пр тр кр волн
Влияние на суммарные потери в решётках оказывают:
а) относительная высота лопаток;
б) относительный шаг;
в) угол поворота в решётке;
г) угол входа потока;
д) число Маха на выходе из решётки;
е) число Рейнольдса на выходе из решётки при дозвуковых
скоростях
75.
Относительный лопаточный КПДДля одиночной ступени или одноступенчатой турбины:
Е0 Н0с Н0 р Н0
Потери с выходной скоростью
с22
Н вс
2
Баланс энергии в ступени:
Е0 Lu H c H p H вс
Lu Е0 H c H p H вс
Н 0 с Н 0 р H c H p H вс
76.
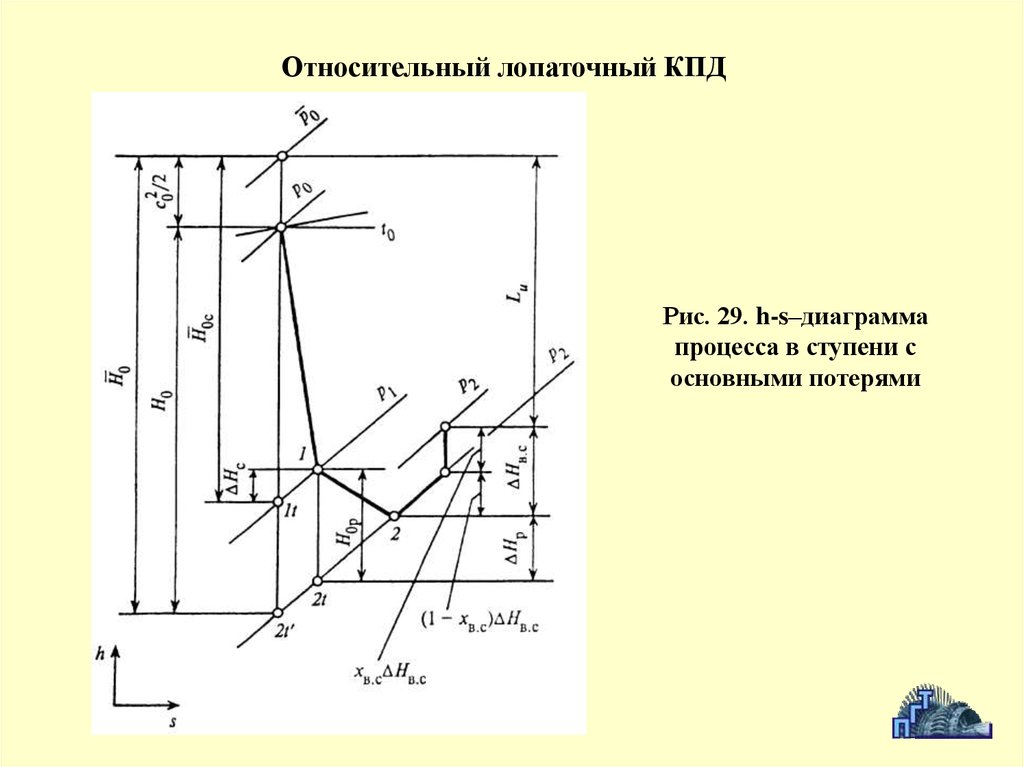
Относительный лопаточный КПДРис. 29. h-s–диаграмма
процесса в ступени с
основными потерями
77.
Относительный лопаточный КПДс
Н 0с
2
2
1t
с12t с12
Н с
2 2
H0 р
w22t w12
2
2
w22t w22
H р
2
2
с22
Н вс
2
Lu Н 0 с Н 0 р H c H p H вс
с12t w22t w12 с12t с12 w22t w22 с22
2
2
2
2 2
2
2
2
с12 с22 w22 w12
2
2
78.
Относительный лопаточный КПДLu
ол
E0
Lu E0 Н E0 Н с Н р Н вс
ол
E0
E0
Н0
Н с
с
Н0
р
Н р
Н0
ол 1 с р вс
Н вс
вс
Н0
79.
Относительный лопаточный КПДс22
Е0 Н 0 вс
2
ол
E0 Н с Н р 1 вс Н вс
Е0
80.
Относительный лопаточный КПД (к выводуН0
сф2
2
Рассмотрим
случай, когда:
Lu
ол
E0
u с
ф опт )
с2t сф
вс 0
Е0 Н 0
0
w2t w1
сф2
2
c1t cф
Lu u w1 cos 1 w2 cos 2
Lu u w1 cos 1 w2 cos 2
ол
E0
сф2 2
81.
Относительный лопаточный КПД (к выводуВ уравнении для КПД второе слагаемое …
…умножим и разделим на
u с
ф опт )
w2 cos 2
w1 cos 1
u
ол 2 2 w1 cos 1 w2 cos 2
сф
u
2 2
сф
w1 cos 1
w1 cos 1 w2 cos 2
w1 cos 1
u
2 2
сф
w2 cos 2
w1 cos 1 1
w1 cos 1
82.
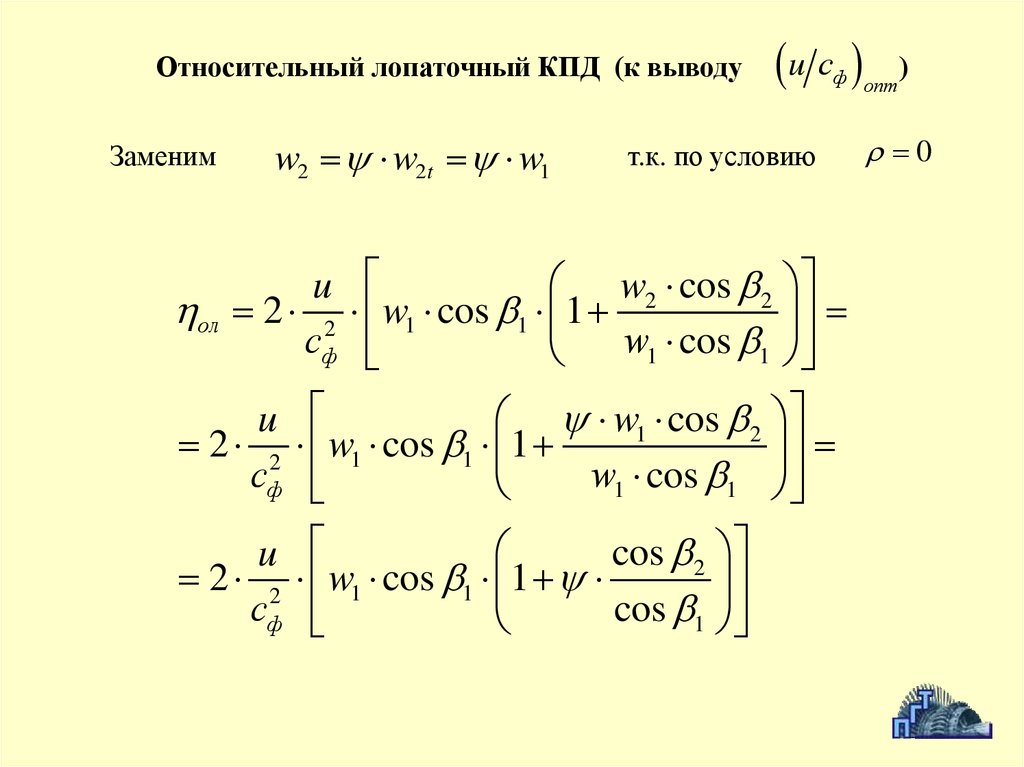
Относительный лопаточный КПД (к выводуЗаменим
w2 w2t w1
u
ол 2 2
сф
u с
ф опт )
т.к. по условию
w2 cos 2
w1 cos 1 1
w1 cos 1
u
2 2
сф
w1 cos 2
w1 cos 1 1
w1 cos 1
u
2 2
сф
cos 2
w1 cos 1 1
cos 1
0
83.
Относительный лопаточный КПД (к выводуu с
ф опт )
Из треугольников скоростей имеем (см. рис.17 (левая сторона)):
w1 cos 1 с1 cos 1 u
Отсюда:
w1 cos 1 с1t cos 1 u сф cos 1 u
u
ол 2 2
сф
cos 2
w1 cos 1 1
cos 1
u
2 2
сф
cos 2
сф cos 1 u 1
cos 1
u
2
сф
cos 2
u
cos 1 1
сф
cos 1
84.
Относительный лопаточный КПД (к выводуu с
ф опт )
Таким образом, относительный лопаточный КПД:
u
ол f ; ; ; 1 ; 2
с
ф
1
не является независимым
параметром, т.к. получается из
треугольника скоростей:
1 f 1; с1; u
Пренебрегая влиянием остальных параметров (т.е. считая их
постоянными), относительный лопаточный КПД:
u
ол f
с
ф
85.
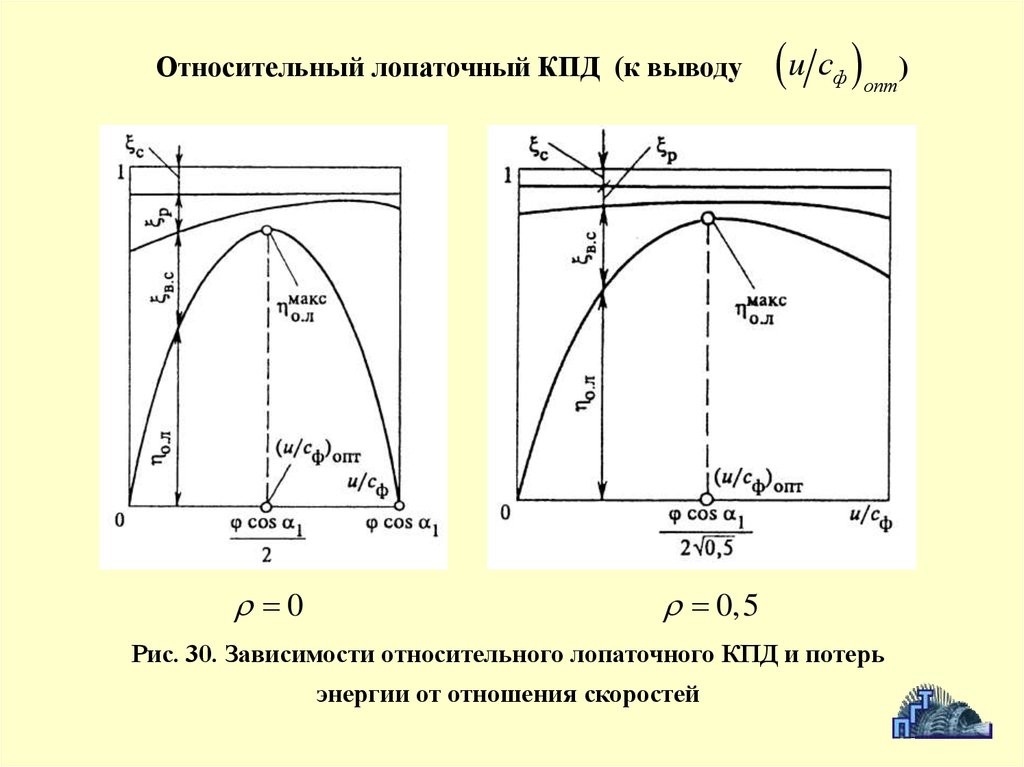
Относительный лопаточный КПД (к выводу0
u с
ф опт )
0,5
Рис. 30. Зависимости относительного лопаточного КПД и потерь
энергии от отношения скоростей
86.
Относительный лопаточный КПД (к выводуmax
ол
ол
u сф
u с
ф опт )
0
0
u
cos 1
2
сф опт
0,5
u
cos 1
сф опт 2 0,5
var
u
cos 1
сф опт 2 1
олmax
олmax
max
ол












































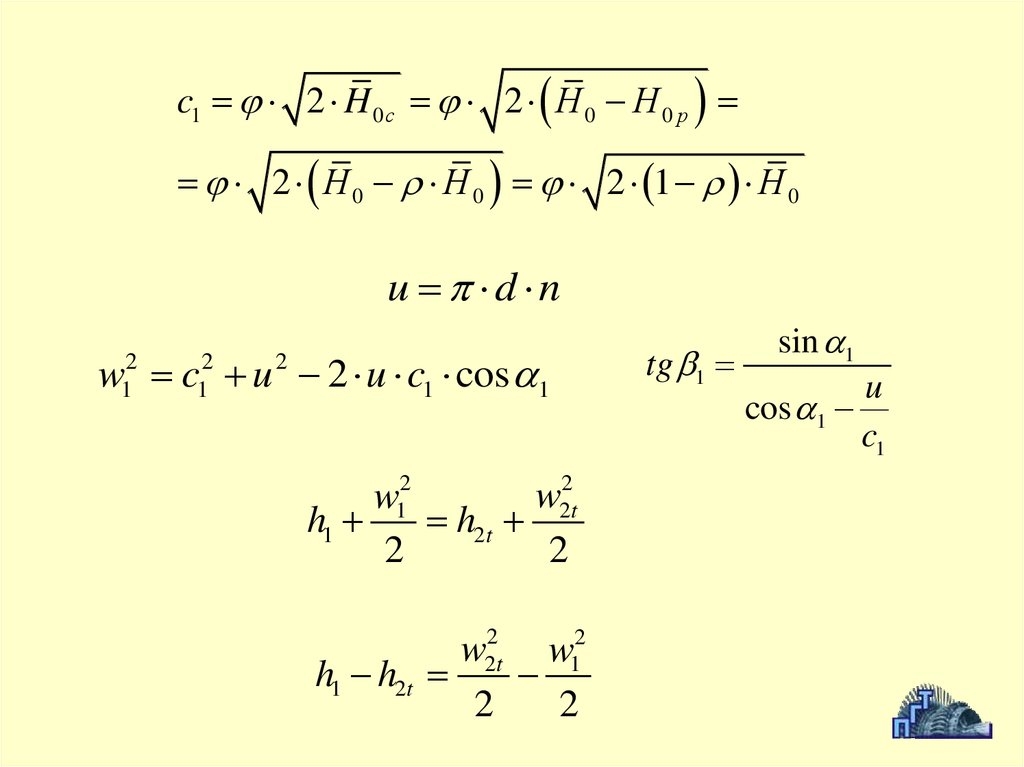

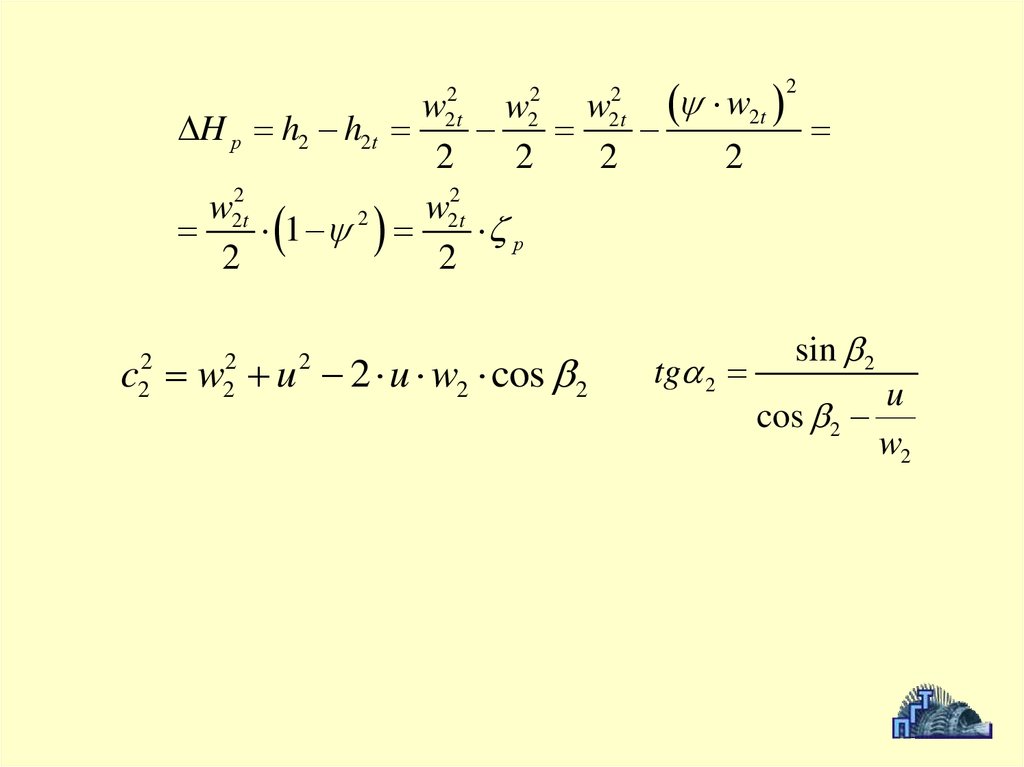
























 Промышленность
Промышленность