Линейная алгебра. Выполнение операций над матрицами

1. Линейная алгебра практическое занятие

2. Примеры. 1. Выполните операции над матрицами

ПРИМЕРЫ.
1. ВЫПОЛНИТЕ ОПЕРАЦИИ
1)
НАД МАТРИЦАМИ

3.

4.

5.

6. 2. Вычислить определитель матрицы

2. ВЫЧИСЛИТЬ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ

7.

8.

9. 3. Вычислить матрицу, обратную данной

3. ВЫЧИСЛИТЬ МАТРИЦУ, ОБРАТНУЮ
ДАННОЙ
2 1 4
A 1
0 2
3 5
8
1) Определитель det A=2*0*8+1*5*4+(-1)*(-2)*(-3)-4*0*(-3)-5*(-2)*2
-1*(-1)*8=0+20-6-0+20+8=42
2) A11 ( 1)^2 0 2 0 * 8 ( 2) * 5 0 10 10;
5
A12 ( 1)^3
A13
1
0
8
1
2
3
8
(8 6) 2;
5 0 5;
3 5
1 4
A21
( 8 20) 28;
5 8
A22
2
4
3 8
16 12 28;

10.

A23
A31
1
0
2
A32
1
2
A33
1
2
1
3
5
4
2
4
(10 3) 7;
2 0 2;
( 4 4) 8;
2
1
0 1 1.
0
10 2 5
~
3) A 28 28 7 ;
2
8
1
10 28 2
~T
4) A 2 28 8 ;
5 7 1
10 28 2
1
5) A 1 2 28 8 .
42
5 7 1

11.

Сделаем проверку
10 28 2 1 0 0
2 1 4
1
А· А = 1 0 2 2 28 8 = 0 1 0 Е .
3 5
42 5 7 1 0 0 1
8
-1
Элемент (11): 2*10+(-1)*(-2)+4*5=42
Элемент (12): 2*28+(-1)*28+4*(-7)=0
Элемент (13): 2*2+(-1)*8+4*1=0
Элемент (21): 1*10+0*(-2)+(-2)*5=0
Элемент (22): 1*28+0*28+(-2)*(-7)=42
Элемент (23): 1*2+0*8+(-2)*1=0
Элемент (31): (-3)*10+5*(-2)+8*5=0
Элемент (32): (-3)*28+5*28+8*(-7)=0
Элемент (33): (-3)*2+5*8+8*1=42

12. 4. Найти ранг матрицы

4. НАЙТИ РАНГ
2
1
А=
1
1
МАТРИЦЫ
1 1 1
2 0 1
3 0 1
4 1 2
Поменяем вторую и первую строки местами (для ручного счета удобно,
чтобы элемент a11 был равен 1 или -1 (если это возможно)).
1
2
Получим матрицу
1
1
2 0 1
1 1 1
3 0 1
4 1 2
В дальнейшем первую строку менять не будем. Теперь с помощью элемента
a11 =-1 образуем нули в первом столбце, во второй, третьей и четвертой
строках. Для этого ко второй строке прибавим первую, умноженную на число
2, из третьей строки вычтем первую, к четвертой прибавим первую строку:
1
0
0
0
2 0 1
5 1 3
1 0 0
6 1 3

13.

Поменяем местами в этой матрице вторую и третью строки, и в дальнейшем
первая и вторая строки меняться не будут. И с помощью элемента 1 получим
нули во втором столбце в третьей и четвертой строках:
1
0
0
0
2 0 1 1
1 0 0 0
5 1 3
0
6 1 3 0
2 0 1
1 0 0
0 1 3
0 1 3
Здесь из третьей строки вычли вторую, умноженную на 5, а из четвертой –
вторую, умноженную на 6.
Из четвертой строки вычтем третью, получим матрицу:
1
0
0
0
2 0 1
1 0 0
0 1 3
0 0 0
Угловые элементы -1, 1, 1, их число равно 3. следовательно, ранг матрицы
равен 3.

14. 5. Решить систему уравнений

5. РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ
x1 5 x 2 4 x3 16
Найти решение системы уравнений методом Крамера 3 x1 x 2 8
.
3 x 2 x x 11
2
3
1
1
5
4
3
1
0 1 24 0 12 0 15 2;
3
2
1
16 5 4
1 8
1 0 16 64 0 44 0 40 4;
11 2 1
1 16 4
2 3
8
0 8 132 0 96 0 48 4;
3 11 1
1 5 16
3 3 1
8 11 96 120 48 16 165 2.
3 2 11
Итак, х1
4
4
2
2; х 2
2; х1
1.
2
2
2

15.

Решим систему уравнений методом Гаусса
Составим расширенную матрицу и приведем ее к ступенчатому виду:
4
16 1 5
4
16
1 5 4 16 1 5
3 1 0 8 0 14 12 40 0 14 12 40 .
3 2 1 11 0 13 11 37 0 0
2
2
Первую строку перепишем, и в дальнейшем менять не будем. С помощью
элемента 1 получим нули в первом столбце. Для этого умножим первую
строку на 3 и вычтем ее из второй и третьей строк. Получим вторую матрицу.
Далее с помощью второй строки получаем нули во втором столбце, третьей
строке. Для этого умножим вторую строк на (-13), третью – на 14 и сложим.
Получим третью (последнюю) матрицу.
На основе последней матрицы запишем эквивалентную ступенчатую
систему:
x1 5 x 2 4 x3 16
14 х 2 12 x3 40;
2 x 2
3
x1 2
х 2 2.
x 1
3
Из последнего уравнения находим х3, далее переходим ко второму
уравнению, подставляя вместо х3=1 и находим х2 и т.д.
Таким образом, решением данной системы уравнений является вектор
Х (2; 2; 1) .

16. 6. Найти косинус угла между векторами

6. НАЙТИ КОСИНУС УГЛА МЕЖДУ ВЕКТОРАМИ
Даны два вектора а (1,1, 2) и b (2, 1,0) . Найти косинус угла между векторами
c 2a b и d a b .
Решение. Найдем координаты векторов c и d :
c 2 (1,1, 2) (2, 1,0) (2,2, 4) (2, 1,0) (0,3, 4) ;
d (1,1, 2) (2, 1,0) (3,0, 2) .
Вычислим длины векторов c и d :
c 0 2 32 ( 4) 2 5; d 32 0 2 ( 2) 2 13.
Вычислим косинус угла между этими векторами:
cos
(c , d )
c d
0 3 3 0 ( 4) ( 2)
5 13
8
5 13
.

17.

c a b
При
каком
значении
векторы
и
d a b перпендикулярны (ортогональны)? (Координаты векторов a и
b заданы в предыдущем примере).
Пример.
Решение. Найдем координаты векторов c a b и d a b :
c a b (1,1, 2) (2, 1,0) ( 1,2, 2);
d a b (1,1, 2) (2, 1,0) ( , , 2 ) (2, 1,0) ( 2, 1, 2 ) .
Запишем условие ортогональности полученных векторов:
(а b )( a b ) 0;
1 ( 2) 2 ( 1) ( 2) ( 2 ) 0;
2 2 2 4 0;
5 4 0;
4
.
5

18.

a , a , a – проекции
Z
x
a
ay
O
ax
X
i
z
вектора a на оси
координат (или
координаты вектора
az
k
y
j
a ax i a y j az k
Y
a)

19.

Пример. Найти векторное произведение векторов
a 2i 3 j k ,
b 3i j 4 k .
Решение.
a ( 2;3; 1),
b (3; 1; 4)
i
j
k
a b 2
3
1
3 1 4
2
1
3 4
j
2
3
3 1
d ( 13;5; 11)
3
1
1 4
i
k 13i 5 j 11k.

20. 7. Уравнение прямой

7. УРАВНЕНИЕ ПРЯМОЙ
Пример 1. Треугольник АВС задан своими вершинами А(1; 3), В(-2; 0), С(4;1). Составить уравнение средней линии треугольника АВС, параллельной
прямой ВС, и высоты, опущенной из вершины А.
Решение. а) Найдем середины отрезков АВ и АС (точки М и N
соответственно):
M(
5
1 4 3 ( 1)
1 3
1 ( 2) 3 0
) N ( ;1) .
;
) M ( ; ) ; N (
;
2
2
2
2 2
2
2
Составим уравнение прямой MN по двум точкам:
x x1
y y1
;
y 2 y1 x2 x1
3
1
3
1
1
x
y
x
x ( ) y
2;
2
2;
2
2 2 y 3 ; x 1 6 y 9 ;
1
3
1
5
2
3
1
3
( ) 1
2
2
2
2
17
1
y x
- уравнение средней линии треугольника АВС, параллельной ВС.
12
6

21.

б) Из вершины А треугольника АВС опустим перпендикуляр АН, и составим
уравнение этой прямой.
Прежде всего составим уравнение прямой ВС:
y y1
x x1
;
y 2 y1 x2 x1
x 2 y
1
1
1
x ( 2) y 0
; 6 y x 2 ; y x ; k BC .
;
6
1
6
3
6
4 ( 2) 1 0
1
Так как BC AH k BC k AH 1, k AH
6.
1
6
Тогда, уравнение прямой АН с угловым коэффициентом
k AH 6 и
проходящей через точку А(1;3) имеет вид:
y y 0 k ( x x0 ) ;
y 3 6( x 1) ;
y 6 x 3 - уравнение высоты треугольника АВС, опущенной из вершины А.

22.

Пример 2. Составить уравнение прямой, проходящей
через точки М1(2; 3) и М2(3; –1).
y y1
x x1
Решение. Воспользуемся формулой:
y2 y1
y 3 x 2
1 3 3 2
x2 x1
y 3 x 2
4
1
Разрешим полученное уравнение относительно у:
y 3 4( x 2)
y 4 x 11.
y 3 4 x 8

23. 8. Кривые второго порядка

8. КРИВЫЕ ВТОРОГО ПОРЯДКА
Пример 1. Привести к каноническому виду уравнение второго порядка
х 2 у 2 2х 4 у 4 0 .
Решение. Сгруппируем члены, содержащие х, и отдельно члены, содержащие
у, и выделим их полные квадраты.
х 2 у 2 2х 4 у 4 0 ;
( х 2 2 х) ( у 2 4 у ) 4 0 ;
( х 2 2 х 1) 1 ( у 2 4 у 4) 4 4 0 ;
( х 1) 2 ( у 2) 2 9 ;
( х 1) 2 ( у 2) 2 32 .
Мы получили уравнение окружности с центром в точке С(1, -2) и радиусом,
равным 3.

24. Окружность

ОКРУЖНОСТЬ
Окружность - геометрическое место
точек, равноудаленных от точки О (центр).
x 2 y 2 R 2 - уравнение окружности с
радиусом R и центром в начале
координат;
( x x0 )2 ( y y0 )2 R 2
- с центром в точке (x0,y0);

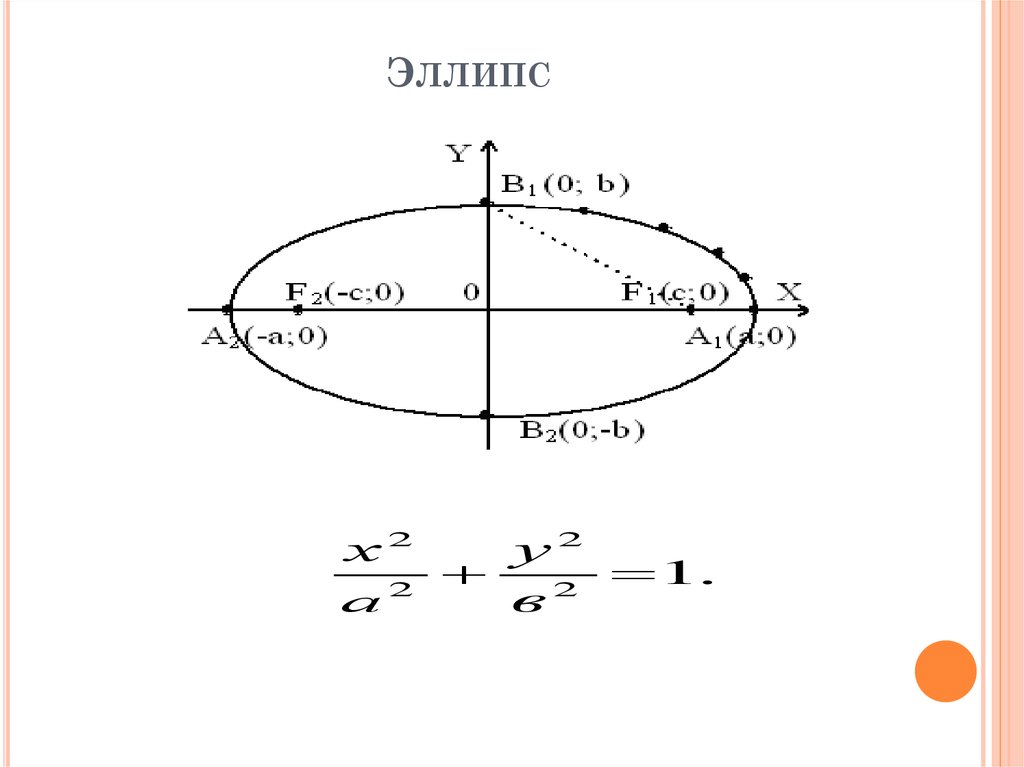
25. Эллипс

ЭЛЛИПС
х2
у2
1.
2
2
а
в

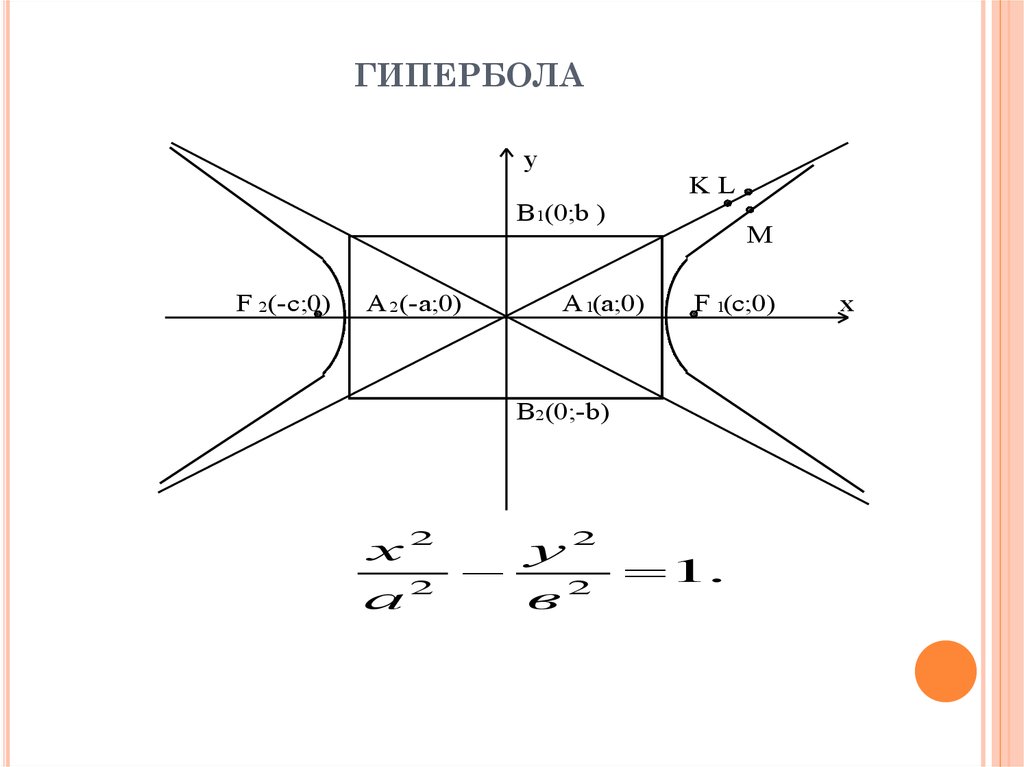
26. гипербола

ГИПЕРБОЛА
y
KL
B1(0;b )
F 2(-c;0)
A 2(-a;0)
A 1(a;0)
M
F 1(c;0)
B2(0;-b)
х2
у2
1.
2
2
а
в
x

27. парабола

ПАРАБОЛА
y
0
y 2 px,
2
F
x
y
F
0
x 2 2 py.
x

28.

Пример 2. Составить каноническое уравнение эллипса, зная, что расстояние
между фокусами равно 8, а малая полуось b 3 .
Решение. По условию, 2c 8, c 4, b 3 .
Мы знаем, что b 2 а 2 с 2 , a 2 b 2 c 2 , a 2 32 4 2 25, a 5 .
Итак, каноническое уравнение эллипса имеет вид
х2 у2
1.
25 9

29.

Пример 3. Установите, какую линию определяет уравнение
3 2
y 7
x 6 x 13, y 7, x R.
2
Нарисуйте ее график.
Пример 4. Установите, какую линию определяет
уравнение
1
x 1
2
Пример
уравнение
y 1
.
2
Нарисуйте ее график.
5. Установите, какую
линию
y 2 9 x 8 x .
2
Нарисуйте ее график.
определяет

30. Пример 3.

ПРИМЕР 3.
ОЗФ:
y 7.
y 7
3 2
4
2
x 6 x 13 , y 7 x 2 6 x 13 .
9
2
Выделим в правой части полный квадрат:
4
2
2
( y 7)2 ( x 3)2
1
y 7 x 3 4 ,
9
9
4
- гипербола, О(3, 7), полуоси а = 2, b = 3.
Исходное уравнение
3 2
x 6 x 13,
y 7
2
y 7
определяет
нижнюю ветвь гиперболы, расположенную под
прямой y=7.

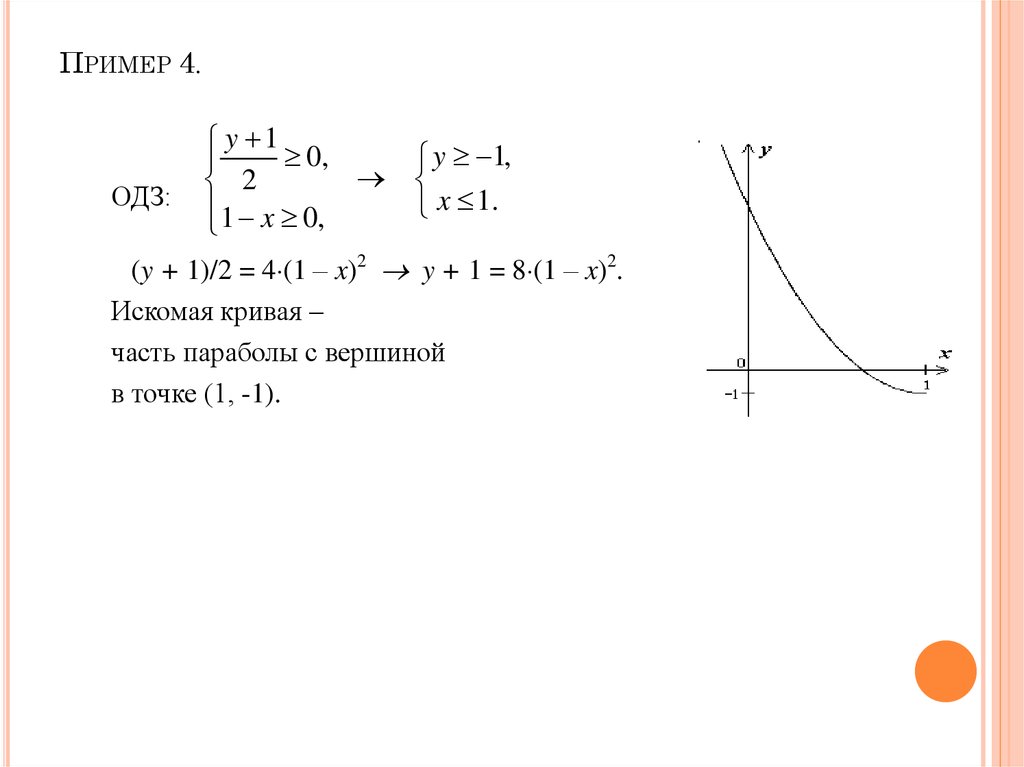
31. Пример 4.

ПРИМЕР 4.
ОДЗ:
y 1
0,
y 1,
2
x 1.
1 x 0,
(y + 1)/2 = 4 (1 – x)2 y + 1 = 8 (1 – x)2.
Искомая кривая –
часть параболы с вершиной
в точке (1, -1).

32. Пример 5.

ПРИМЕР 5.
Искомая кривая –
часть окружности:
(y + 2)2 + (x – 4)2 = 52,
y -2, x [-1, 9].

33. Пример 6.

ПРИМЕР 6.
Определить тип кривой и схематически построить ее
9 x 2 25 y 2 36 x 150 y 414 0
Решение. Приведем заданное уравнение к каноническому виду. Для
этого в исходном уравнении выделим полные квадраты по
переменным х и у. Перепишем исходное уравнение в виде:
9 x 2 36 x 25 y 2 150 y 414 0,
9( x 2 4 x ) 25( y 2 6 y) 414 0,
9( x 2 2 2 x 2 2 2 2 ) 25( y 2 2 3y 32 32 ) 414 0,
9[( x 2) 2 4] 25[( y 3) 2 9] 414 0,
9( x 2) 2 36 25( y 3) 2 225 414 0,
9( x 2) 2 25( y 3) 2 225,
( x 2) 2
( y 3) 2
1.
25
9

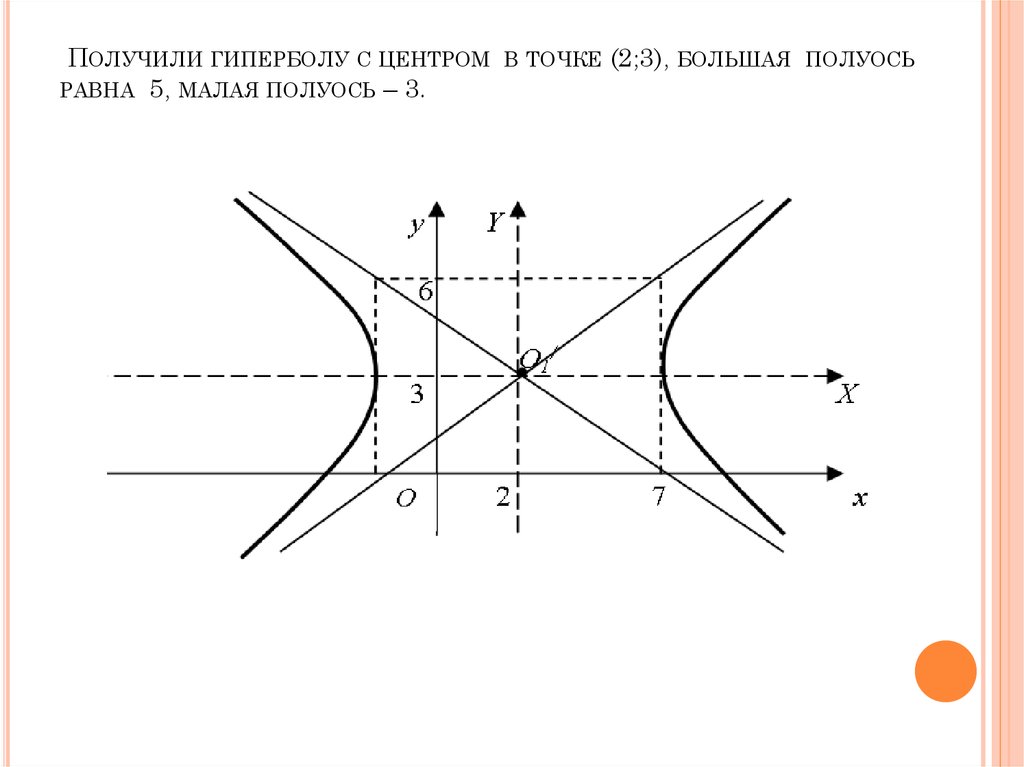
34. Получили гиперболу с центром в точке (2;3), большая полуось равна 5, малая полуось – 3.

ПОЛУЧИЛИ ГИПЕРБОЛУ С ЦЕНТРОМ В ТОЧКЕ (2;3), БОЛЬШАЯ ПОЛУОСЬ
РАВНА 5, МАЛАЯ ПОЛУОСЬ – 3.

35. МАТЕМАТИЧЕСКИЙ АНАЛИЗ (практическое занятие)

36. пределы

ПРЕДЕЛЫ
Пример 1. Вычислить предел
1)
lim
x
2)
3
3
0
x 5
3
2
(
x
6
x
5 x 1)
lim
x
3x 2 5 x 4
3) lim 2
x
2
x
3
x
3x 2 5 x
4
5
2 2
3
х2
х
х lim
x
lim
x
2
x2 2x
3
x
1
2
2
2
x
х
х
х
3 0 0
3
1 0 0
4
5
4
3
х2
3
2
3
1
х2

37.

Пример 2. Вычислить предел
1
1
lim (
3
)
x 1 x 1
x 1
Решение.
1
1
1
1
lim (
3 ) lim (
)
2
x 1 x 1
x 1 x 1
x 1
( x 1)( x x 1)
x x 1 1
x x 2
lim
lim 3
3
x 1
x 1 x 1
0
x 1
2
2

38. Пример 3.

ПРИМЕР 3.

39. пример

ПРИМЕР

40.

Пример 5. Вычислить предел
:
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность 0/0
Общее правило: если в числителе и знаменателе находятся многочлены, и
имеется неопределенность вида 0/0, то для ее раскрытия нужно разложить
числитель и знаменатель на множители.
Очевидно, что можно сократить на (х+1)
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

41.

Пример 6.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела это первое,
что нужно выполнять для ЛЮБОГО предела.
Получена неопределенность вида 0/0 ,
которую нужно устранять
Когда в числителе (знаменателе) находится разность корней (или корень минус какоенибудь число), то для раскрытия неопределенности используют метод умножения
числителя и знаменателя на сопряженное выражение.

42.

43. Примеры 7, 8

ПРИМЕРЫ 7, 8
sin( 2 x )
0
2 sin( 2 x )
sin( 2 x )
( ) lim
2 lim
2 1 2.
x 0
x
0
x
0
x
0
2x
2x
lim
е
4
3

44. Пример 9. Вычислить предел

ПРИМЕР 9. ВЫЧИСЛИТЬ ПРЕДЕЛ
Решение.
x
x 1
x 1
1
lim
lim lim
lim 0
x 2 x 2
x x 2 x 2
x 2
x
Пример 10. Вычислить предел
x
1 cos x
x 0
x2
lim
Решение. Преобразуем числитель и знаменатель дроби
x
1 cos x 2 sin
2
2
x
x 2 4
2
2
2
x
x
2 sin 2
sin
1 cos x
2 lim 1
2 11 1
lim
lim
2
x 0
x 0
x 0 2
x
2
2
x2
x
4
2
2

45. Производная функции

ПРОИЗВОДНАЯ ФУНКЦИИ
Пример 1. Вычислить первую и вторую производную,
x
дифференциал функции
y
x2 1
Решение
y
1( x 2 1) x(2 x)
x
1
2
dy y dx
2
x2 1
x
2
x2 1
x
2
1
2
1
2
dx
x 1
y y 2
2
x 1
2 x ( x 2 1)2 ( x 2 1)2( x 2 1) 2 x 3 4 x 2 2 x 4
4
3
2
2
x 1
x 1
2
45

46. Пример 2

ПРИМЕР 2
y 3x cos(1 x 2 )
Решение. Обозначим: f1(x)=3x; f2(x)= cos(1-x2)
Функция
f 2( x) cos(1 x 2 )
- сложная функция. Тогда
y (3x cos(1 x 2 )) 3 cos(1 x 2 ) 3x( sin( 1 x 2 )( 2 x)
3(cos(1 x 2 ) 2 x 2 sin( 1 x 2 ))
dy y dx 3 (cos(1 x 2 ) 2 x 2 sin( 1 x 2 ))dx
y 3 (( sin( 1 x 2 )( 2 x) 4 x(sin( 1 x 2 ) 2 x 2 ( cos(1 x 2 )( 2 x))
46

47. Пример 3.

ПРИМЕР 3.
y e x ln sin x
Решение. Обозначим
f 1( x) e x ; f 2( x) ln sin x
Тогда
1
y (e ) ln sin x e (ln sin x) e ln sin x e
( cos( x))
sin x
1
x
dy y dx e (ln sin x
cos( x)) dx
sin x
x
x
x
x
1
1
x
x cos x
y (e (ln sin x
cos( x))) e (ln sin x ctgx) e (
2 )
sin x
sin x sin x
x
47

48.

Пример 4. Вычислить производную функции
x
y
sin x cos x
x (sin x cos x) x(sin x cos x) sin x cos x x cos x x sin x
y
(sin x cos x) 2
(sin x cos x) 2

49.

50. Пример 5. Исследовать функцию g(x) и построить ее график

g ( x) 5( x 2)e x 1
1)
2)
3)
4)
5)
Область определения - R.
Функция непериодическая.
Четность/нечетность - функция общего вида.
Точки пересечения с осью ОХ: y = 0 x = 2
c осью OY: х = 0 ; у=-10\е ;
y 0 при x 2;
y 0 при x ( ; 2)

51. Экстремумы, возрастание, убывание

g ( x) 5e x 1 5( x 2)e x 1 5e x 1 ( x 1) 0
x 1
x
( ; 1]
g’
-
+
g
убывание
возрастание
xmin 1
[1; )

52. Выпуклость/вогнутость

x 1
x 1
x 1
g ( x) 5e 5( x 1)e 5e x 0
x 0 точка перегиба
x ( ; 0) y 0 выпуклость
x ( 0; ) y 0 вогнутость

53.

54. Интегральное исчисление

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример 1. Вычислить
x
2
3x 3 x 1 dx .
Решение. Так как под знаком интеграла находится
сумма четырех слагаемых, то раскладываем интеграл
на сумму четырех интегралов:
2
3
2
3
x 3 x x 1 dx x dx 3 x dx xdx dx .
x3
x4 x2
3
x C
3
4
2

55.

Пример 2. Вычислить
x ln xdx
dx
u ln x, du
x
2
x
dv xdx, v
2
x2
x 2 dx
=
ln x
2
2 x
x2
1
x2
1 x2
=
ln x xdx
ln x
C .
2
2
2
2 2

56. Пример 3. Вычислить интеграл

ПРИМЕР 3. ВЫЧИСЛИТЬ ИНТЕГРАЛ
Найти
1 x
1 x
2
dx
tdt
1 t
2
x t, x t 2 ,
dx 2tdt
2
t2
1 t
2
dt
1 t
1 t
d (t 2 1)
t
2
1
2
2tdt
2
dt
ln(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln( x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt

57. Пример 4.

ПРИМЕР 4.
Вычислить интеграл
xe
3 x 2 4
dx
Сделаем замену t 3x 2 4 , тогда dt 6xdx ,
следовательно xdx
xe
3 x 2 4
dt
.
6
dt
1 t
1 t
1 3 x 2 4
dx e ( ) e dt e C e
C
6
6
6
6
t

58. Пример 5.

ПРИМЕР 5.
x sin xdx x d ( cos x)
u
v
x( cos x) ( cos x)dx
x cos x sin x C

59. Пример 6.

ПРИМЕР 6.
Найти площадь фигуры, ограниченной
линиями: y = 0, y = 1 , x = 1, x = e.
x
y
e
dx
e
S=
ln x 1 ln e ln 1 1 0 1
x
1
x=1
x=e
Ответ: S = 1
y=
1
e
1
x
y=0
x

60. Пример 7.

ПРИМЕР 7.
Вычислить площадь фигуры, ограниченной линиями:
1
y 1 cos x, y 0, x , x
2
2
2
2
1
S (1 cos x)dx
2
2
x
y
2
2
1
2
1
( x sin x) 1
2
y=0
2
Ответ: S = π+1
x
2
2
x

61. Пример 8.

ПРИМЕР 8.
Вычислить площадь фигуры, ограниченной
линиями y=x-2 и y=x2-4x+2
y
1.
y=x2-
4x+2, xв =2, yв = -2
2. у=х-2: х=0, у=-2; х=2, у=0
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4
4. S= ((x 2) ( х 4 x 2))dx
2
1
4
2
3
4
5x
x
(5 x x 4)dx (
4 x) 4,5
2
3
1
1
Ответ: S=4,5
1
2
-2
4
x

62. Пример 9.

ПРИМЕР 9.
Вычислить площадь фигуры, ограниченной
линиями
и
2
y x 2x 3
y x 2 1