Похожие презентации:
Линейная алгебра. Матрицы и действия над ними
1.
ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Матрицы и действия
над ними
Челябинск, 2018
2. Раздел 1. Линейная алгебра.
РАЗДЕЛ 1.ЛИНЕЙНАЯ АЛГЕБРА.
Линейная
алгебра
является
необходимым
инструментарием для компактного и эффективного
описания и анализа экономико-математических
моделей и методов.
2
3. Тема 1. Матрицы
ТЕМА 1. МАТРИЦЫПонятие матрицы и основанный на нем раздел математики – матричная
алгебра – имеет важное значение для экономистов, так как значительная часть
математических моделей экономических объектов может быть записана в
компактной матричной форме.
Матрицей называется прямоугольная таблица чисел, содержащая m строк
одинаковой длины (или n столбцов одинаковой длины).
Матрица записывается следующим образом:
Матрицы обозначаются прописными
латинскими буквами.
или
Am n (aij )
где
aij
a11
a21
A
...
am1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
– элемент матрицы, i – ой строки и j – го
столбца,
где
i = 1,2…m
j = 1,2…n
3
4.
Матрицу А называют матрицей размера m n и пишутЧисла
, составляющие матрицу, называется ее
элементами. Элементы, стоящие на диагонали, идущей из
верхнего левого угла, образуют главную диагональ.
Матрицы равны между собой, если равны
соответствующие элементы этих матриц, т.е.,
А=В, если
, где
все
4
5.
Виды матрицЕсли количество строк равно количеству столбцов,
т.е. m=n, то матрица называется квадратной.
Квадратную матрицу размера n × n называют
матрицей n-го порядка.
7 45
À
1
0
Если m = n, то матрица называется прямоугольной.
1
À
0
2
3
2
0
3
5
5
6.
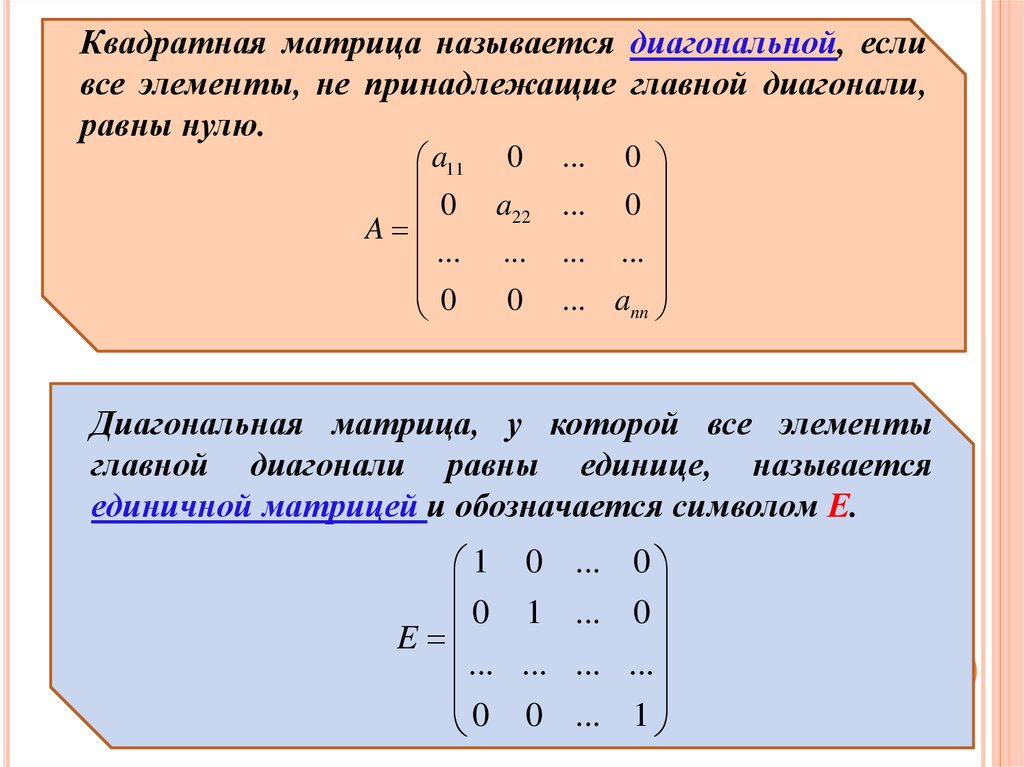
Квадратная матрица называется диагональной, есливсе элементы, не принадлежащие главной диагонали,
равны нулю.
a11
0
A
...
0
0
a22
...
0
0
... 0
... ...
... ann
...
Диагональная матрица, у которой все элементы
главной диагонали равны единице, называется
единичной матрицей и обозначается символом Е.
1
0
E
...
0
0 ... 0
1 ... 0
... ... ...
0 ... 1
6
7.
Квадратная матрица называется треугольной, если всеэлементы, расположенные по одну сторону от главной
диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется
нулевой. Обозначается буквой О. Имеет вид:
0
0
0
...
0
0 ... 0
0 ... 0
... ... ...
0 ... 0
В матричном исчислении матрицы О и Е играют роль
чисел 0 и 1 в арифметике.
7
8.
Матрица, содержащая один столбец или одну строку,называется вектором (или вектор-столбец, или векторстрока соответственно). Их вид:
Матрица размера 1 × 1, состоящая из одного числа,
отождествляется с этим числом, т.е.
есть 5.
9.
Матрица, полученная из данной заменой каждой ее строкистолбцом с тем же номером, называется матрицей
транспонированной к данной. Обозначается
.
Так, если
Транспонированная
свойством: (АТ)Т = А.
матрица
обладает
следующим
10.
Действия над матрицамиСложение
Операция сложения матриц вводится только для матриц
одинаковых размеров.
Суммой двух матриц Am n (aij ) и
называется матрица
такая, что
Записывают С=А+В.
Вычитание
Все свойства сложения соответствуют вычитанию.
10
11.
Пример сложения и вычитания матрицДаны матрицы:
Сумма матриц:
Разность матриц:
11
12.
Умножение на числоПроизведением матрицы Am n (aij ) на число k называется
матрица
такая, что
Записывают B=k A.
Пример:
Матрица – А= (-1) А называется противоположной матрице А.
12
13.
Операции сложения, вычитания и умножения матрицы начисло обладают следующими свойствами:
1) А + В = В + А (коммутативность)
2) А + (В + С) = (А + В) + С – ассоциативность
3) А + 0 = А
4) А – А = 0
5) 1 А = А
6) (А + В) = А + В – дистрибутивность
7) ( + ) А = А + А
8) ( А) = ( ) А
где А, В, С – матрицы, и – числа.
13
14.
Элементарные преобразования матрицЭлементарными преобразованиями матриц являются:
перестановка местами двух параллельных рядов матрицы;
умножение всех элементов ряда матрицы на число, отличное от нуля;
прибавление
ко всем элементам ряда матрицы соответствующих
элементов параллельного ряда, умноженных на одно и тоже число.
Две матрицы называются А и В эквивалентными, если одна из них получается из
другой с помощью элементарных преобразований. Записывается А В.
При помощи элементарных преобразований любую матрицу можно привести к
матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все
остальные элементы равны нулю. Такую матрицу называют канонической, например:
14
15. Пример: Привести к каноническому виду матрицу
ПРИМЕР: ПРИВЕСТИ К КАНОНИЧЕСКОМУ ВИДУ МАТРИЦУРешение: выполняя элементарные преобразования, получаем:
15
16.
Произведение матрицПроизведением матрицы Am n (aij ) на матрицу
называется матрица
такая, что
т.е. элемент i-й строки и k-го столбца матрицы произведения С равен
сумме
произведений
элементов
i-строки
матрицы
А
на
соответствующие элементы k-го столбца матрицы В.
Получение элемента
схематично изображается так:
i
16
k
17.
Если матрицы А и В квадратные одного размера, то произведения АВ иВА всегда существуют. Легко показать, что А Е = Е
А=А, где А –
квадратная матрица, Е – единичная матрица того же размера.
Пример:
17
18.
Пример:Тогда произведение А В
.
не определено, так как число
столбцов матрицы А не совпадает с числом строк матрицы
В. При этом определено произведение В × А, которое
считают следующим образом:
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение
матриц обладает следующими свойствами:
1. А (В С) = (А В) С
2. А (В + С) = АВ + АС
3. (А + В) С = АС + ВС
4. (АВ) = ( А)В
18
19.
Если,конечно,
написанные
суммы
и
произведения матриц имеют смысл.
Для
операции
транспонирования
верны
свойства:
1. (А + В)Т = АТ + ВТ
2. (АВ)Т = ВТ АТ
19
20.
Тема 2. ОпределителиКвадратной матрице А порядка n можно сопоставить
число det A (или А , или
), называемое ее определителем,
следующим образом:
1. n = 1.
2. n = 2.
3.
n = 3.
20
Определитель матрицы А также называют детерминантом.
21.
Вычисление определителя 2-го порядка, иллюстрируется схемой:2
a11
a12
a21 a22
2
a11a22 a12a21
21
22.
Примеры:1)
2)
3)
4)
3 2
1
5
3 5 2 1 15 ( 2) 17
cos x sin x
sin x
cos x
cos 2 x sin 2 x cos 2 x
cos x sin x
sin x
log 2 32
cos x
cos 2 x sin 2 x 1
log 3 27
log 4 16 log 5 125
5 3
2 3
15 6 9
22
23.
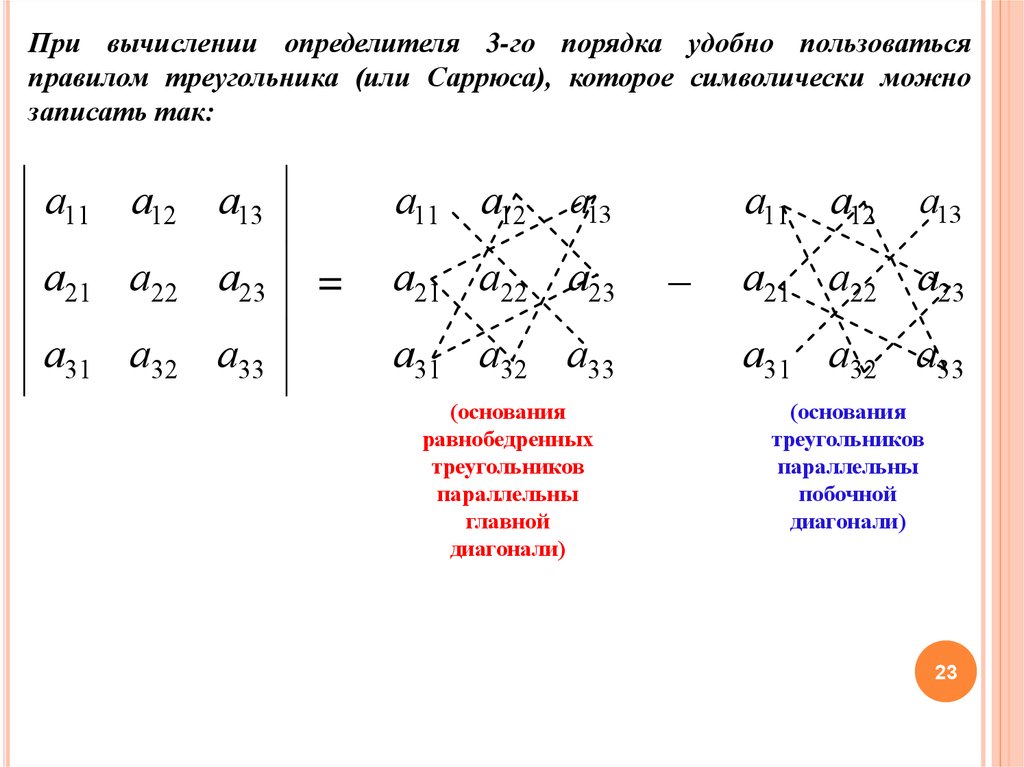
При вычислении определителя 3-го порядка удобно пользоватьсяправилом треугольника (или Саррюса), которое символически можно
записать так:
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11 a12
=
a11 a12
a13
a21 a22 a23
–
a13
a21 a22 a23
a31 a32 a33
a31 a32 a33
(основания
равнобедренных
треугольников
параллельны
главной
диагонали)
(основания
треугольников
параллельны
побочной
диагонали)
23
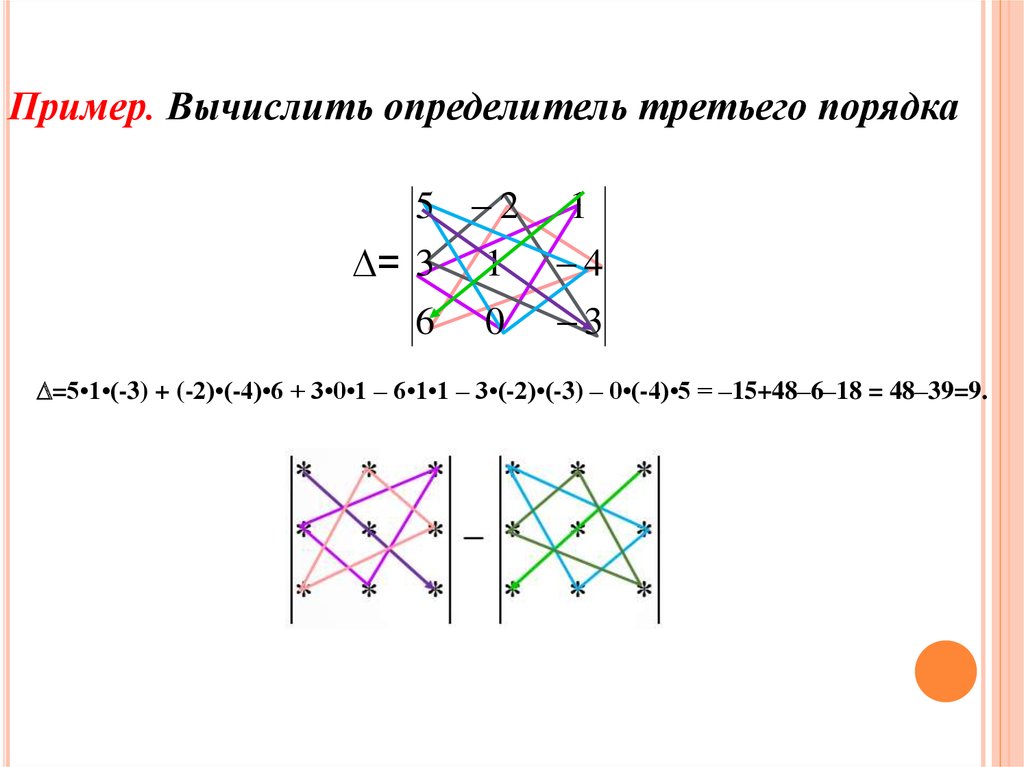
24.
Пример. Вычислить определитель третьего порядка5 2
= 3
6
1
1
4
0
3
=5•1•(-3) + (-2)•(-4)•6 + 3•0•1 – 6•1•1 – 3•(-2)•(-3) – 0•(-4)•5 = –15+48–6–18 = 48–39=9.
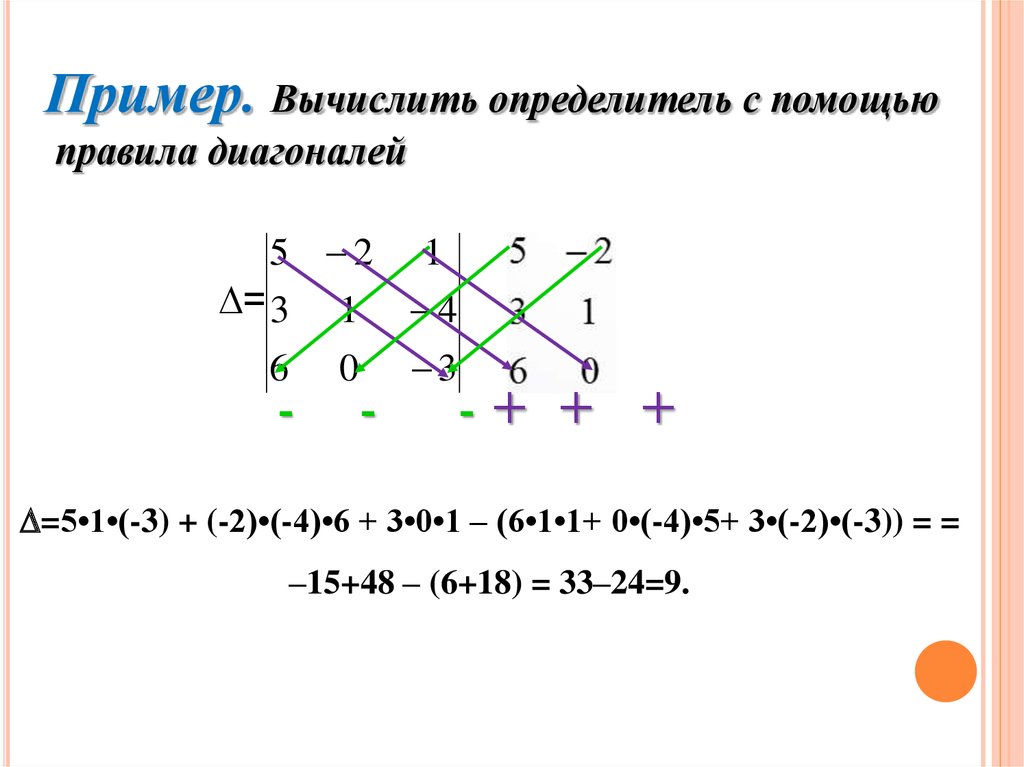
25.
Пример. Вычислить определитель с помощьюправила диагоналей
5 2
1
= 3
1
4
6
0
3
-
-
-+ + +
=5•1•(-3) + (-2)•(-4)•6 + 3•0•1 – (6•1•1+ 0•(-4)•5+ 3•(-2)•(-3)) = =
–15+48 – (6+18) = 33–24=9.
26.
Тема 2.2 Свойства определителей1. Определитель не изменится, если его транспонировать:
det A det A
T
det A
det A
T
3
5
2 4
3 2
5
4
12 10 22
12 10 22
27.
2. При перестановке двух строк или столбцов определительизменит свой знак на противоположный.
3
5
2 4
2 4
3
5
12 10 22
10 12 22
28.
3. Определитель с двумя одинаковыми строками илистолбцами равен нулю.
1
1
3
1
1
3
2 1 4
4 3 6 6 3 4 0
29.
4. Общий множитель всех элементов строки или столбцаможно вынести за знак определителя.
a11
ka12
a21 ka22
k
a11
a12
a21 a22
30.
Пример:1
2
36 12
1
3
2
1
2
2
1
2
1
24 12 3
1
2 12 2 3
1
1
4
1 3 4
1 3 2
24 2 9 2 1 12 3 24 15 360
31.
5. Если все элементы двух строк (или столбцов) определителяпропорциональны, то определитель равен нулю.
3 7
1
3 7
1
1 2 2 3 1 2 0 0
4 6 2
2 3 1
2 3
32.
6. Если каждый элемент какого-либо ряда определителяпредставляет собой сумму двух слагаемых, то такой
определитель равен сумме двух определителей, в первом из
которых
соответствующий
ряд
состоит
слагаемых, а во втором- из вторых слагаемых.
из
первых
33.
a1 j b1 j... a1n
a21 ... a2 j b2 j
... a2 n
...
...
a11 ...
...
...
anj bnj
an1 ...
...
... ann
a11 ... a1 j
... a1n
a11 ... b1 j
... a1n
a21 ... a2 j
... a2 n
a21 ... b2 j
... a2 n
...
...
...
...
...
...
an1 ... anj
...
... ann
...
...
an1 ... bnj
...
... ann
34.
7. Если к какой-либо строке (или столбцу) определителяприбавить соответствующие элементы другой строки (или
столбца) , умноженные на одно и то же число, то
определитель не изменится.
a11
a12
a21 a22
к
×
a11
a12
ka11 a21 ka12 a22
35.
5 10
2
10 0 10
5 1 ×2
0
2
+
5
1
10
0
0 10 10
36.
8. Треугольный определитель равен произведениюэлементов главной диагонали.
a11
0
a21
a22
a31
a32
0
a11
a12
a13
0 0
a 22
a 23 a11 a 22 a33
a33
0
0
a33
37. Привести определитель к треугольному виду и вычислить его:
ПРИВЕСТИ ОПРЕДЕЛИТЕЛЬ КТРЕУГОЛЬНОМУ ВИДУ И ВЫЧИСЛИТЬ ЕГО:
2 1 4
1 2 4
×(-2)
×(-5)
7 2 3 2 7 3
7 5 5
5 7 5
1
2
4
0
3
5
0 3 15
=
1 2
+
4
5 60
0 0 20
0 3
38. Разложение определителя по элементам строки или столбца.
РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПОЭЛЕМЕНТАМ СТРОКИ ИЛИ СТОЛБЦА.
Минором
элемента
det D называется
такой новый определитель, который получается
из данного вычеркиванием i-ой строки и j-го
столбца содержащих данный элемент.
39.
a11a12
a13
det D a 21
a 22
a 23
a31
a32
a33
a11
a12
a13
det D a 21
a 22
a 23
a31
a32
a33
M12
M 23
a21 a23
a31 a33
a11
a12
a31 a32
40.
Алгебраическимдополнением
Aij
элемента aij det D называется минор Mij
i j
этого элемента, взятый со знаком 1
т.е.
Aij 1
i j
M ij
41.
Aij 1i j
a11
a12
a13
det D a 21
a 22
a 23
a31
a32
a33
A12 1
1 2
M 12 1
A22 1
2 2
M 22
M ij
a21 a23
a31
a33
a11
a13
a31 a33
42.
Теорема:Сумма
произведений элементов любой строки
(или столбца) определителя на их алгебраические
дополнения равна этому определителю.
43.
разложение по i-ой строке:n
det D ai1 Ai1 ai 2 Ai 2 ... ain Ain aik Aik , i 1,..., n
k 1
разложение по j-му столбцу:
n
det D a1 j A1 j a2 j A2 j ... anj Anj akj Akj ,
k 1
j 1,..., n
44. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
РАЗЛОЖИТЬДАННЫЙ
ЭЛЕМЕНТАМ:
ОПРЕДЕЛИТЕЛЬ
3-ЕЙ
1)
СТРОКИ;
СТОЛБЦА.
1
2
3
4
0 1
5
2
3
2
1 4
1
1
3 2
ПО
2) 1-ГО
45. 1) Разложим данный определитель по элементам 3-ей строки:
1) РАЗЛОЖИМ ДАННЫЙ ОПРЕДЕЛИТЕЛЬЭЛЕМЕНТАМ 3-ЕЙ СТРОКИ:
ПО
det D a31 A31 a32 A32 a33 A33 a34 A34
a31 1 M 31 a32 1 M 32
4
5
a33 1 M 33 a34 1 M 34
6
7
46.
23 1 1
4
3
5
4
1
2 2 1 0
5
3 2
1
1
2
3
4
5
2
1 3 2
4
1
2
1 1 0 1 2 4 1 0 1
6
7
1
1
2
3 36 2 2 4 4 11 56
1
1
3
5
3
47. 2) Разложим данный определитель по элементам 1-го столбца:
2) РАЗЛОЖИМ ДАННЫЙ ОПРЕДЕЛИТЕЛЬЭЛЕМЕНТАМ 1-ГО СТОЛБЦА:
ПО
det D a11 A11 a21 A21 a31 A31 a41 A41
a11 1 M 11 a21 1 M 21
2
3
a31 1 M 31 a41 1 M 41
4
5
48.
11 1 2
2
1
2
3 1 1
4
1
5
2
2
1 4 0 1 2
3
3 2
3
5
2
2 1 1 1
20 0 3 36 32 56
4
1 4
1 3 2
4
3 2
3
5
2
3
4
5
2
1 4
49. Основные методы вычисления определителя.
ОСНОВНЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯОПРЕДЕЛИТЕЛЯ.
1. разложение определителя по
или столбца;
элементам
2.
метод эффективного понижения
3.
приведение определителя к треугольному виду.
порядка;
строки
50.
Метод эффективного понижения порядка:Вычисление определителя n-го порядка сводится к
вычислению одного определителя (n-1)-го порядка,
сделав в каком-либо ряду все элементы, кроме одного,
равными нулю.
51.
12
3
4
0 1
5
2
3
2
1 4
1
1
3 2
×(-3)
×(-1)
1
2
3
4
0
1
5
2
0 4 10 8
0
1
6
2
52.
12
2
3
4
1
0 1
5
2
0 1 5 1
0
5
4
2
2 2 1
0 1 6 2
4 1 1 2
1
2
5 2
0
1
6 1
5 2 4 14 56
6 1
3 2
0
1 5 1
2
2
53. Вычислить определитель приведением его к треугольному виду.
ВЫЧИСЛИТЬОПРЕДЕЛИТЕЛЬ ПРИВЕДЕНИЕМ
ЕГО К ТРЕУГОЛЬНОМУ ВИДУ.
1
2
3
4
0 1
5
2
3
2
1 4
1
1
3 2
×(-3)
×(-1)
1
2
3
4
0
1
5
2
0 4 10 8
0
1
6
2
54.
12
2
3
4
1
0 1
5
2
0 1 5 1
0
5
4
2
2 2 1
4
2
3 2
0 1 5 1
2
5 2
0
1
6 1
2
3
2
0 1
5
1
0
2
5 2
0
0
15 4
0
1
6 1
0
0
11 2
1
×2
4
+
3 2
0
0 1 6 2
1
2
55.
14
2
3
1
2
3
0 1 1
5
0 1 1
5
0
0
4 15
0
0
2 11
1
4
2
2
2
3
0 1 1
5
0
0
2
11
0
0
0 7
4
2
0
0
2 11
0
0
4 15
4 14 56
×(-2)
56.
ТЕМА 3. ОБРАТНАЯ МАТРИЦА57.
Квадратнаяматрица
порядка
n
называется
невырожденной, если её определитель не равен нулю.
n det A
a11
a12
... a1n
a 21
a 22
... a 2 n
...
...
...
a n1
an 2
... a nn
...
0
В противном случае (detA=0) матрица А называется
вырожденной.
58.
Если А- квадратная матрица, то обратной по отношению кматрице
А
называется
матрица,
которая
будучи
умноженной на А (как справа, так и слева) даёт единичную
матрицу.
1
1
A A A A E
59.
Еслиобратная матрица существует, то
матрица А называется обратимой.
Операция
вычисления обратной матрицы
при условии, что она существует,
называется обращением матрицы.
60.
Теорема.Для того, чтобы квадратная матрица А
имела
обратную,
необходимо
и
достаточно, чтобы матрица А была
невырожденной (det А≠ 0).
61. Нахождение обратной матрицы:
НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ:A
где
A
T
A11
A12
...
A
1n
1
A
T
det A
An1
... An 2
... ...
... Ann
A21 ...
A22
...
A2 n
присоединенная матрица
62. Чтобы найти обратную матрицу:
ЧТОБЫ НАЙТИ ОБРАТНУЮ МАТРИЦУ:1.
находят det A и убеждаются, что det A ≠ 0;
2. находят алгебраические дополнения
всех
элементов матрицы А и записывают новую
матрицу А*;
3. транспонируют новую матрицу A
T
;
1
4. умножают полученную матрицу на
det A
63.
Пример 1.Найти матрицу, обратную к матрице А:
1 2 3
A 0 1 2
3 0 7
64. 1) находим определитель матрицы А:
1) НАХОДИМ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ А:1
2
3
det A 0 1 2 14 0 A
3
0
7
1
65. 2) находим алгебраические дополнения всех элементов матрицы А:
2)НАХОДИМ АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ ВСЕХ
ЭЛЕМЕНТОВ МАТРИЦЫ
A11 1
2
1 2
0
7
7
A12 1
0 2
A13 1
0 1
3
4
3 7
3
0
А:
6
3
A21 1
3
2 3
0 7
A22 1
1 3
A23 1
1 2
4
5
3 7
3 0
14
2
6
66.
A31 14
2
3
1 2
A32 1
1 3
A33 1
1
5
6
0 2
2
0 1
7
2
1
67. записываем новую матрицу:
63
7
ЗАПИСЫВАЕМ НОВУЮ МАТРИЦУ: A 14 2 6
7
2
1
3) транспонируем эту матрицу:
A
T
7 14 7
6
2 2
3
6
1
68. 4) умножим полученную матрицу на
4) УМНОЖИМ ПОЛУЧЕННУЮ МАТРИЦУ НА1
A
A
det A
1
T
1
det A
7 14 7
1
6
2 2
14
3
6
1
147
6
14
3
14
1
142
6
14
12
3
7
143
7
14
2
14
1
14
1
17
3
7
17
141
1
2
69. Проверка:
ПРОВЕРКА:A 1 A A A 1 E
1 2 3 147
6
1
A A 0 1 2 14
3 0 7 3
14
Ответ:
12
3
1
A 7
3
14
1
142
6
14
1
17
3
7
1 0 0
2
14 0 1 0
141 0 0 1
7
14
1
7
141
1
2
70. Решение матричных уравнений.
РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ.A X B
1
X A B
1
A
A X A B
1
X
A
A B A
E
E
1
E X A B
1
X A B
X E B A
X B A 1
1
1
71.
Пример 2.Найти матрицу Х:
A X C B
A X C B
1
1
1
A
A X C
C A B C
E
E
1
E X E A B C
1
X A B C
1
1
1
72.
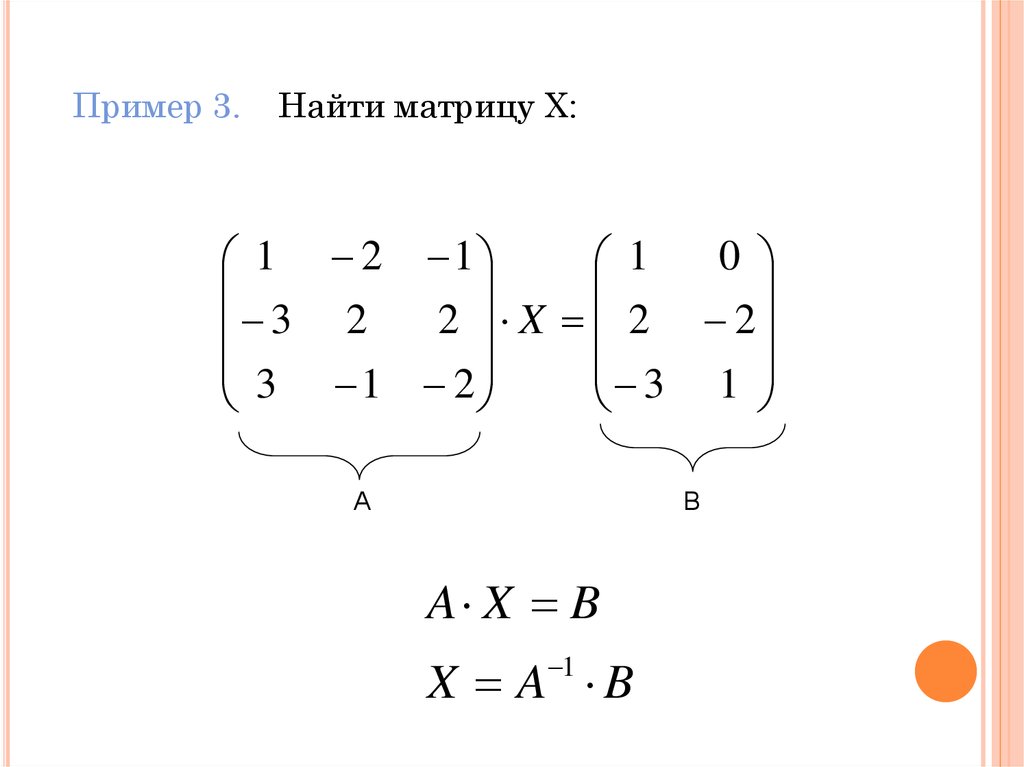
Пример 3.Найти матрицу Х:
0
1 2 1
1
2 X 2 2
3 2
3 1 2
3 1
А
В
A X B
1
X A B
73.
21
1) det A 3
2)
A11
1 2
A13
2
2
1 2
A12
2 1 0 A 1
2
3
2
1
3
2
3
2
3
2
3
1
0
3
A21
A22
1
2
1
1 2
1
3 2
A23
1 2
3 1
3
1
5
74.
A312 1
2
A32
A33
2
2
1
1
3
2
1
2
3
2
1
4
2 0 3
A 3 1 5
2 1 4
75.
3)4)
A
T
2 3 2
0
1
1
3 5 4
1
A
A
det A
1
T
2 3 2
0
1
1
3 5 4
76.
5)0 2 4
2 3 2 1
1
X A B 0
1
1 2 2 1 1
3 5 4 3 1 1 6
Проверка:
1 2 1 2 4 1 0
A X 3 2
2 1 1 2 2 B
3 1 2 1 6 3 1
77.
Ответ:2 4
X 1 1
1 6
78.
Пример 4. Показать, чтоAB
1
1
B A
1
79.
A BX CABX C
Пусть
AB X C
1
1
AB
AB
X AB C
E
X AB C
1
1
BX A C
1
1
1
B
B
X
B
A
C
X B 1 A 1 C
1
X C AB C
C
1
X C 1 B 1 A 1 C
C
E
XC AB
1
E
E
1
1
1
1
A
A
BX
A
C
1
Получили, что
E
XC 1 B 1 A 1
AB
1
B 1 A 1






























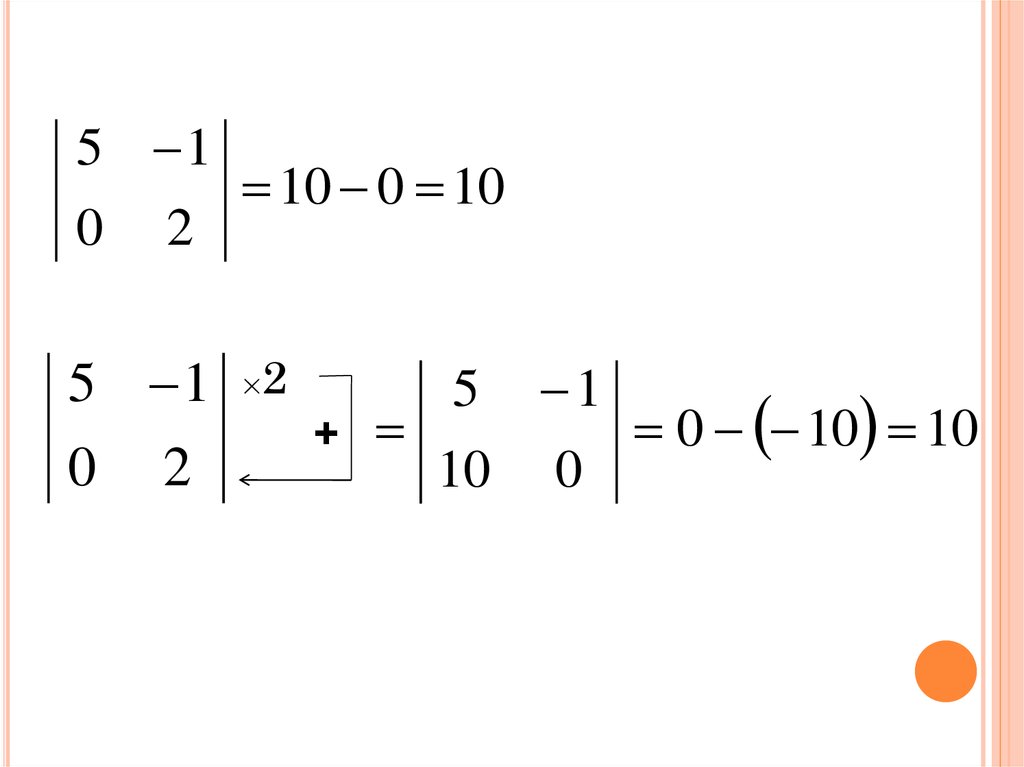



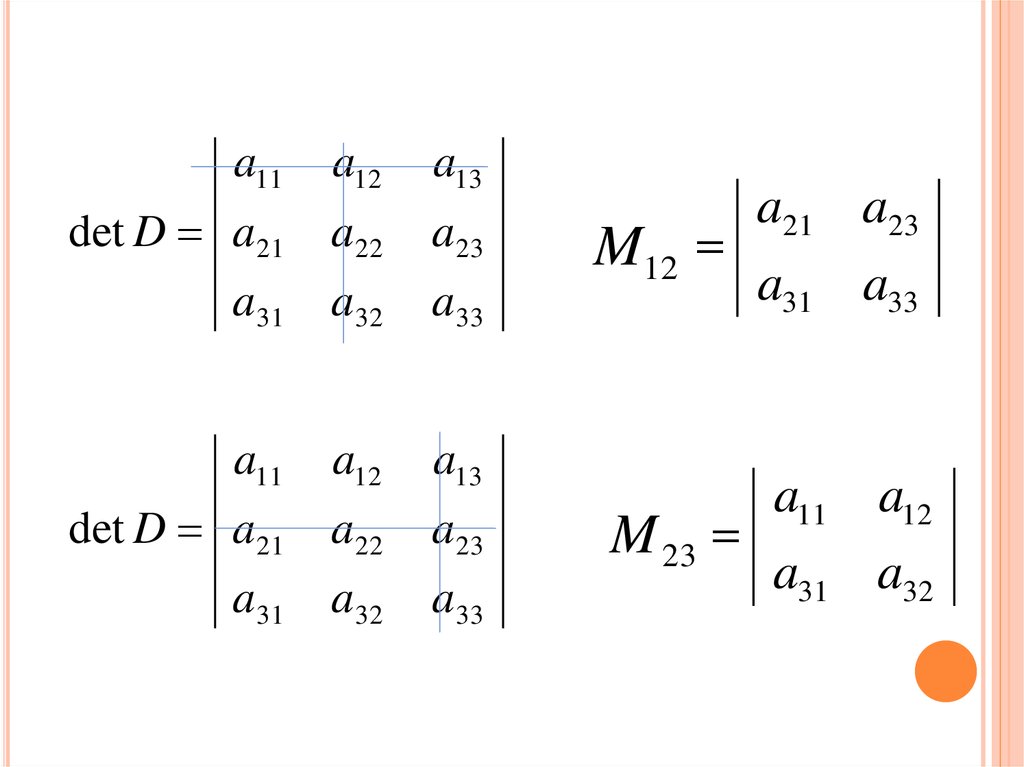

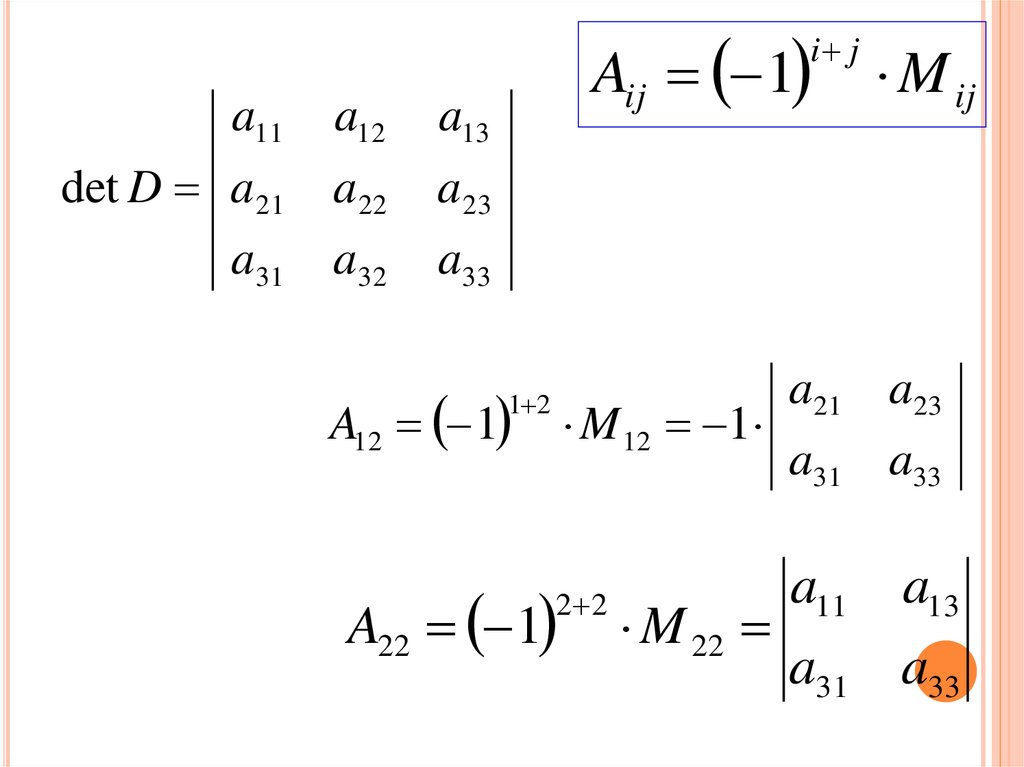

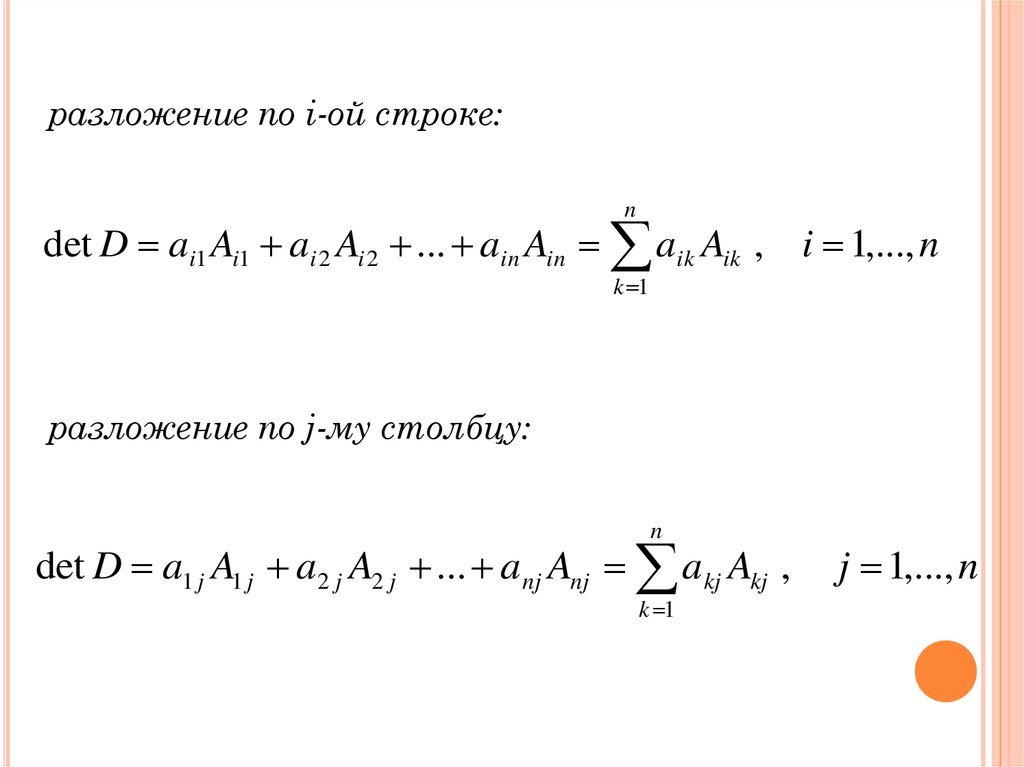


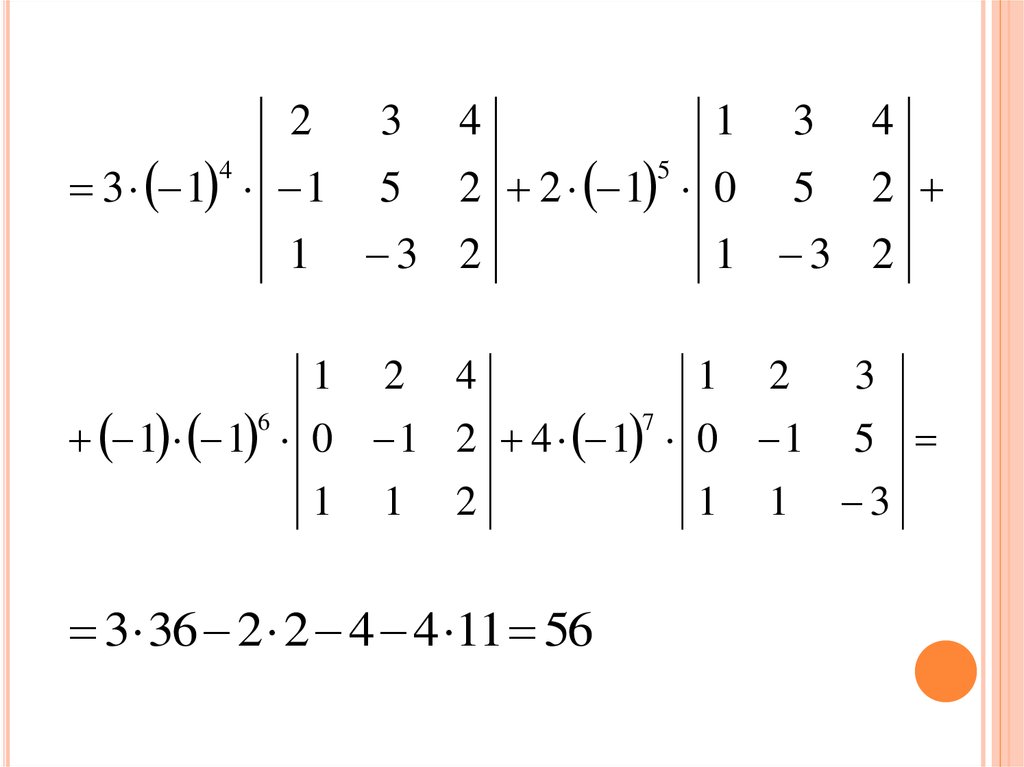

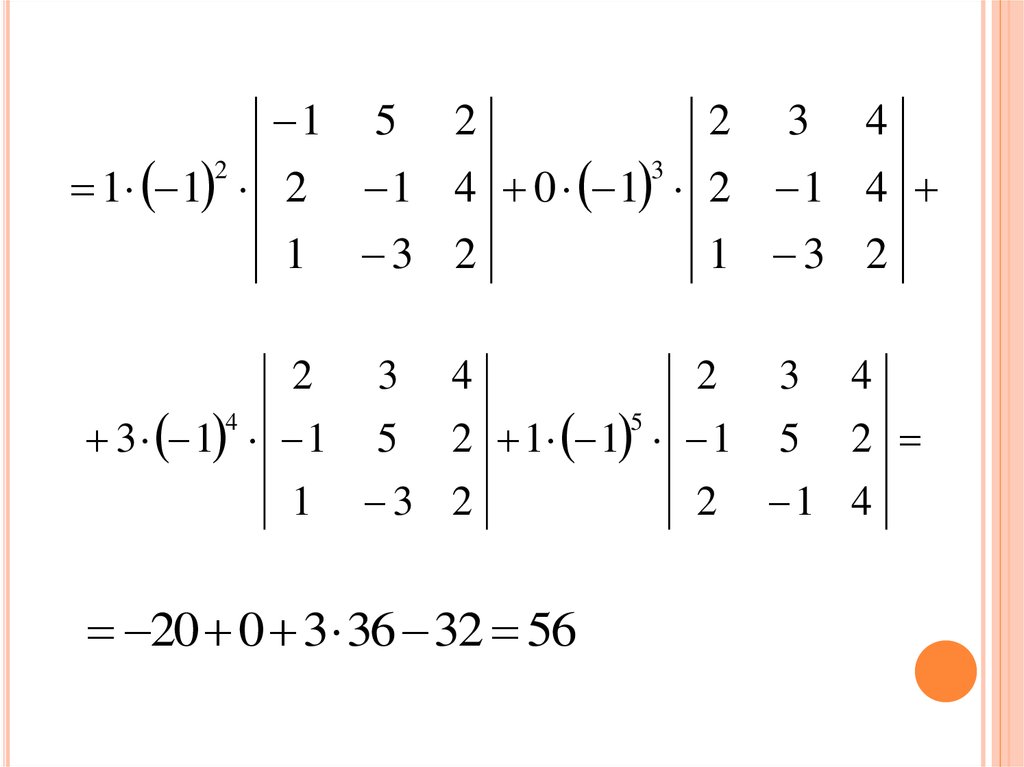

















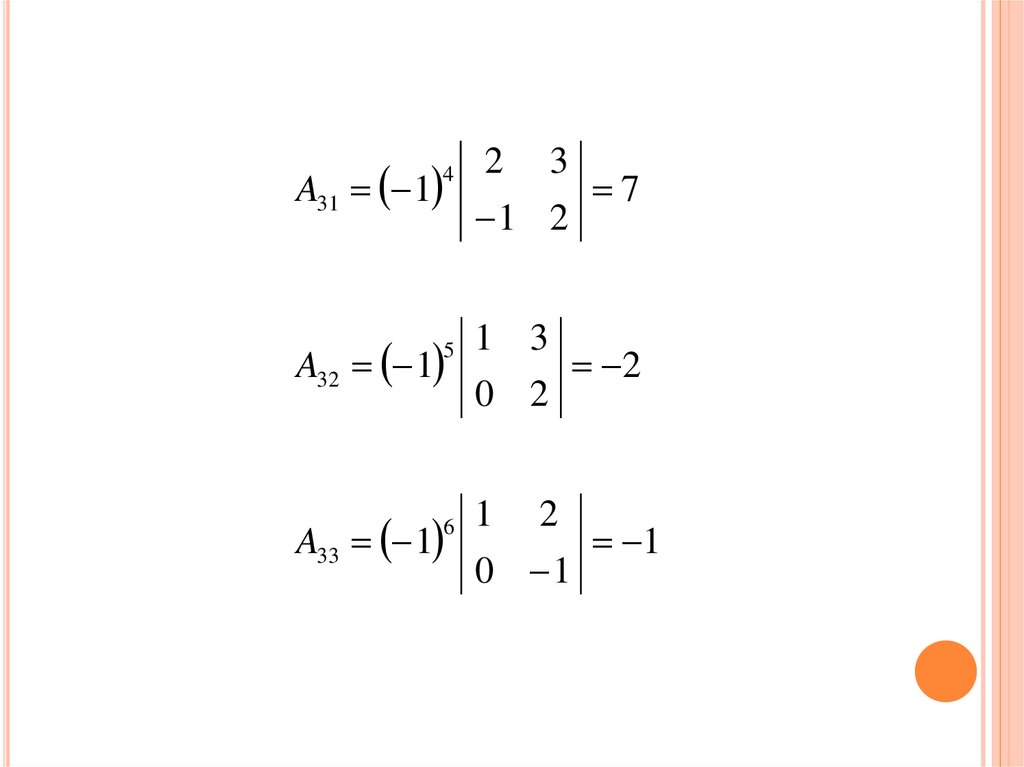




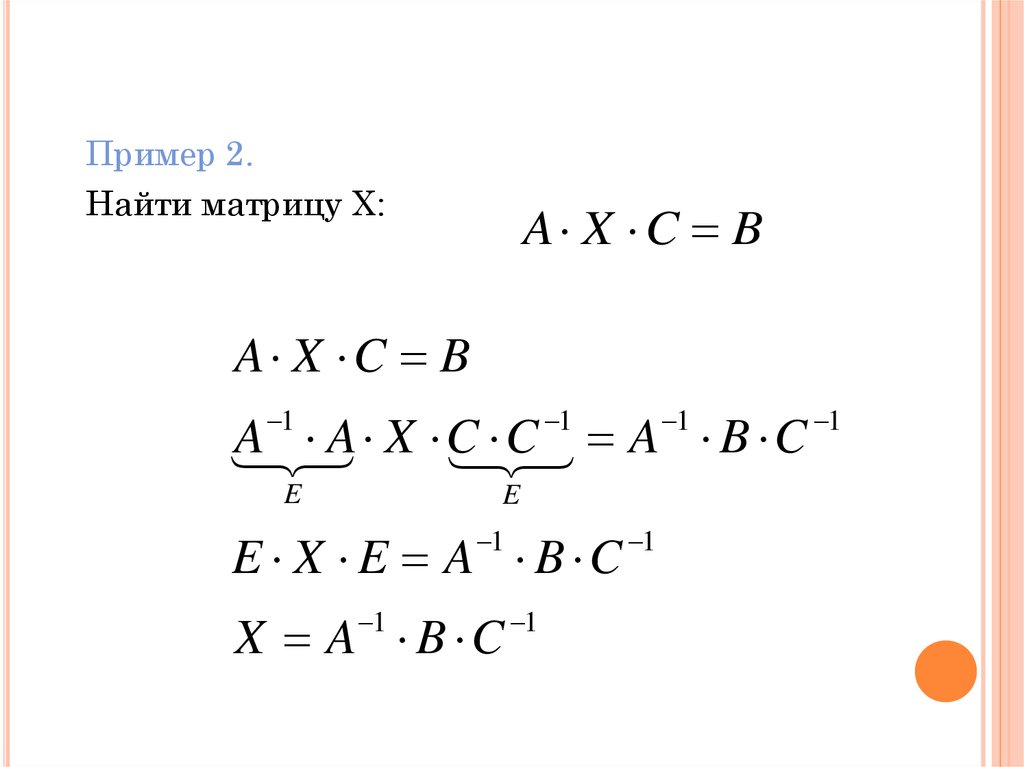
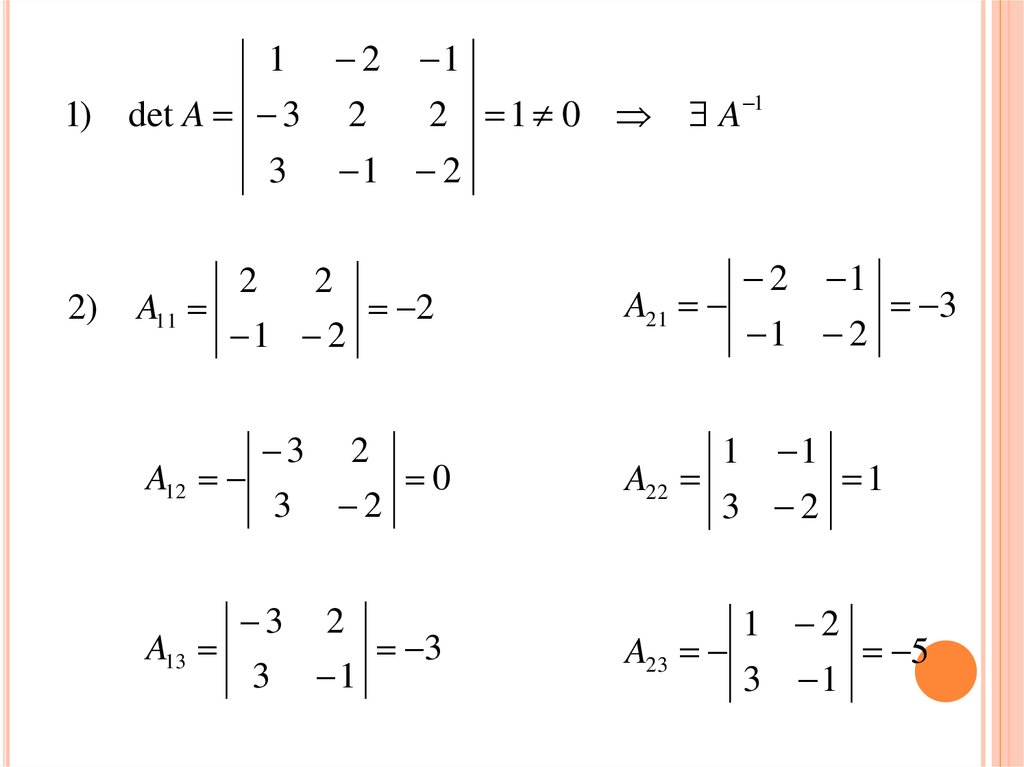
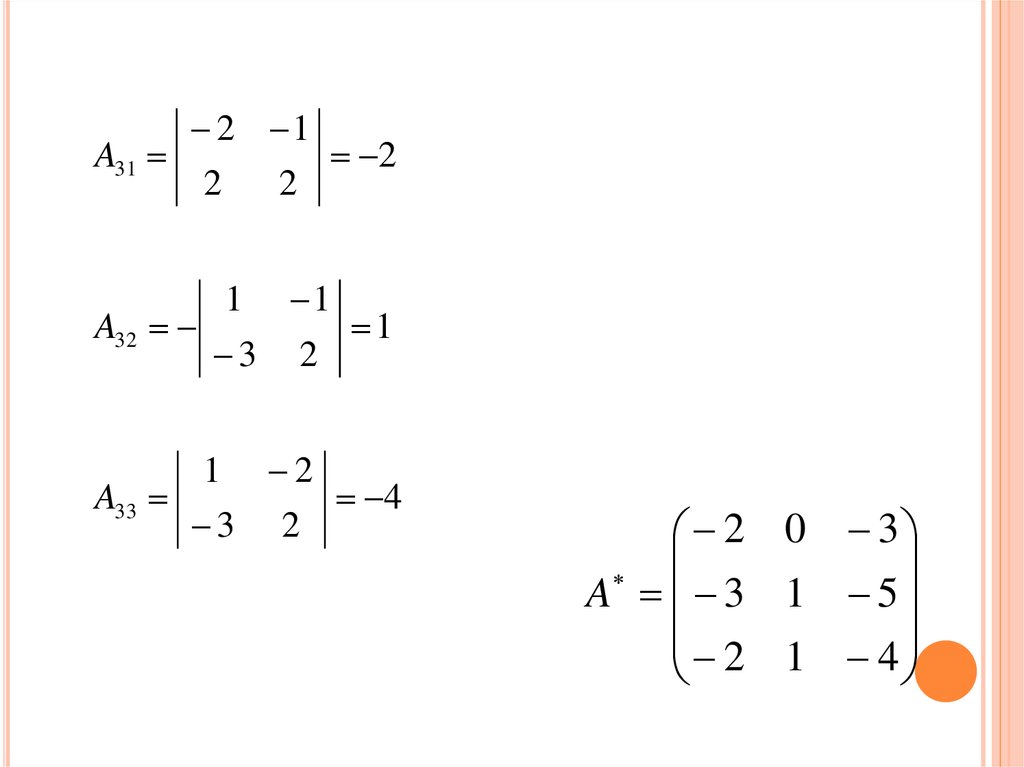

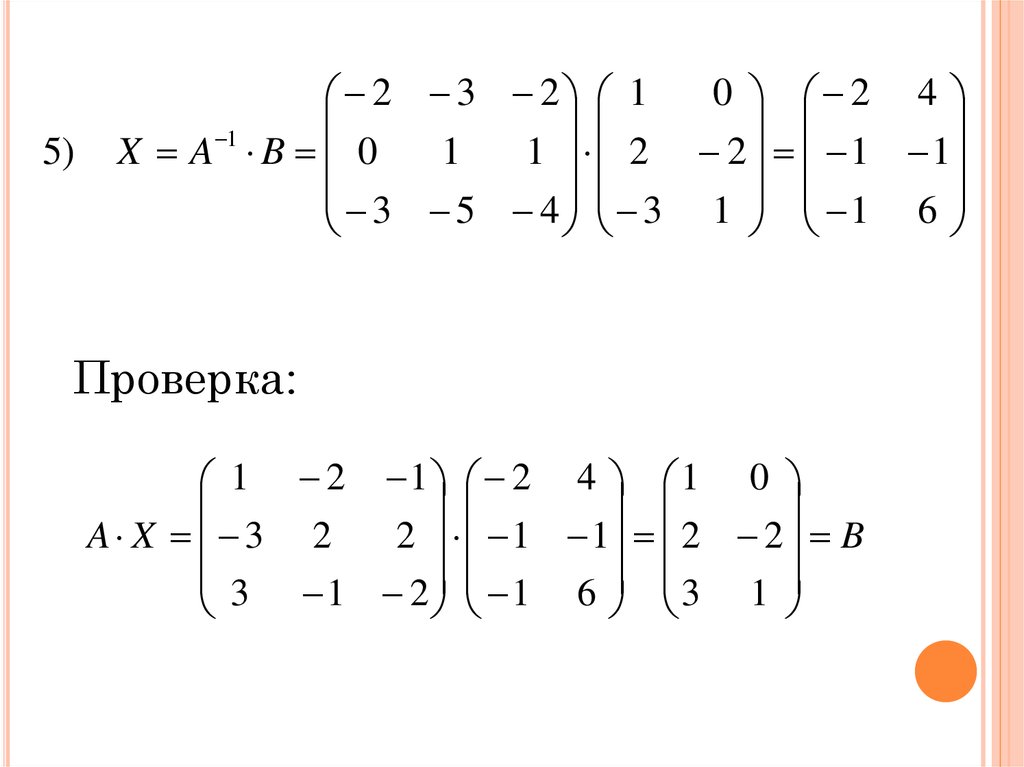



 Математика
Математика








